Abstract
Purpose:
The aim of this research was to compare different methods of calibrating multiple choice question (MCQ) and clinical decision making (CDM) components for the Medical Council of Canada’s Qualifying Examination Part I (MCCQEI) based on item response theory.
Methods:
Our data consisted of test results from 8,213 first time applicants to MCCQEI in spring and fall 2010 and 2011 test administrations. The data set contained several thousand multiple choice items and several hundred CDM cases. Four dichotomous calibrations were run using BILOG-MG 3.0. All 3 mixed item format (dichotomous MCQ responses and polytomous CDM case scores) calibrations were conducted using PARSCALE 4.
Results:
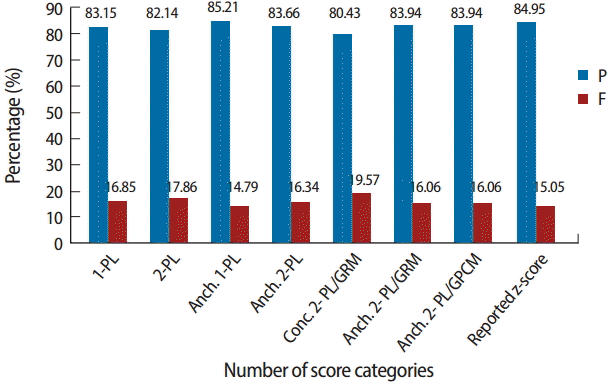
The 2-PL model had identical numbers of items with chi-square values at or below a Type I error rate of 0.01 (83/3,499 or 0.02). In all 3 polytomous models, whether the MCQs were either anchored or concurrently run with the CDM cases, results suggest very poor fit. All IRT abilities estimated from dichotomous calibration designs correlated very highly with each other. IRT-based pass-fail rates were extremely similar, not only across calibration designs and methods, but also with regard to the actual reported decision to candidates. The largest difference noted in pass rates was 4.78%, which occurred between the mixed format concurrent 2-PL graded response model (pass rate= 80.43%) and the dichotomous anchored 1-PL calibrations (pass rate= 85.21%).
Go to : 
The goal of this study was to compare item response theory (IRT)-based ability estimates and pass fail-decision consistency rates to those actually reported for all first-time test takers who completed a form of the Medical Council of Canada’s Qualifying Examination Part I (MCCQEI) in either 2010 or 2011. We investigated both polytomous (e.g. Graded Response Model/Partial Credit Model) and dichotomous (IRT 2-parameter logistic (PL) model) calibration models for forming this MCCQEI composite. Specific goals of our study were as follows: What is the preferred method of calibrating the multiple choice question (MCQ) and clinical decision making (CDM) components of the MCCQEI examination?; What is the correlation between MCQ and CDM question-based expected true-scores? The result of this study will be useful to determine how to best apply an integrated IRT framework to both MCQ and CDM components to form an overall MCCQEI composite.
Go to : 
The sample consisted of 8,213 candidates who completed a form of the MCCQEI for the first time in the spring and fall 2010 and 2011 test administrations. In doing so, we eliminated any re-takers from the analysis sample. The data set contained several thousand multiple-choice items and several hundred CDM cases, the latter further subdivided into CDM questions. Note that 59% of CDM cases had 2 score categories, 31% of CDM cases had 3 score categories, 10% of CDM cases had 4 score categories while less than 1% of CDM cases had 5 score categories. The data were stored as a sparse matrix with connectivity i.e., common or repeated MCQ and CDM cases/questions across test administrations. Although not all candidates saw the exact same number of items, most examinees were presented with 196 MCQs and 36 live CDM cases plus 4-5 pilot cases. On average, each candidate saw 247 total items, including MCQs and CDM questions.
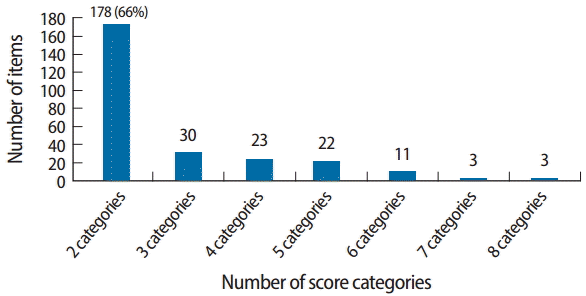
We examined 4 dichotomous calibration designs and 3 mixed format (dichotomous MCQ responses and polytomous CDM case scores) calibration designs. For the dichotomous calibrations, CDM questions were artificially dichotomized to permit the analysis. As a reminder, CDM questions are usually scored on a proportion-correct scale, which reflects the proportion of key features correctly provided or identified in the item. For the purpose of the dichotomous calibrations, “all or nothing” was attributed to each CDM question. Fig. 1 provides the actual number of categories originally contained in the 270 CDM questions. As can be seen, two thirds of the CDM questions were truly dichotomous in nature and did not require any collapsing across categories. This resulted in a total of 3,499 items (3,229 MCQs and 270 CDM questions) for the dichotomous IRT calibrations.
Four dichotomous calibrations were run using BILOG-MG 3.0 [1]. The first 2 dichotomous calibrations were done using a 1-PL model whereas the remaining 2 calibrations employed a 2-PL model. For each pair of analyses, a concurrent calibration was run to simultaneously estimate parameters for both the MCQs and CDM questions, with a resulting overall MCCQEI ability for each candidate. Two additional anchored calibrations were also run using the 1-PL and 2-PL model. In order to conduct the anchored calibrations, the 3,229 MCQs were first calibrated on their own. Next, the IRT parameters for the 270 dichotomized questions were estimated in an anchored calibration run, i.e., by “fixing” the MCQ parameters estimated in the previous step. Finally, an overall MCCQEI ability was estimated for each candidate using the latter parameters. In order to obtain a single ability estimate (θ), a composite theta was created by taking the product of:
The latter weighting scheme is identical to the one that was in in place for the MCCQEI examination up until the fall of 2014.
All 3 mixed item format calibrations were conducted using PARSCALE 4 [2]. The mixed format calibrations combined the 3,229 items with 178 CDM polytomous case scores. Polytomous CDM case scores were created by summing, rounding and integerizing (proportion-correct) question scores for each given case. For example, if a candidate obtained CDM question scores of 0.33, 0.67, and 1.0 on a given case, their overall case score would be equal to 2 for the purpose of the mixed format IRT calibration. In the first mixed item format calibration, all MCQs and CDM case scores were concurrently calibrated using a 2-PL model for the MCQs and a graded-response model (GRM) for the polytomous items. In order to obtain convergence, the concurrent calibration was restricted to 3,100 MCQ items (dropping 129 MCQs for which the 2-PL model did not fit) and 178 CDM case scores. Two additional mixed format anchored calibrations were also run. In the first calibration, CDM case IRT parameters were estimated using the GRM model by fixing the MCQ 2-PL parameters, as estimated previously in BILOG-MG 3. Similarly, in the final mixed format calibration, CDM case IRT parameters were estimated using the generalized partial-credit model (GPCM) by fixing the MCQ 2-PL parameters, as estimated previously in BILOG-MG 3. The anchored calibrations applied the same weighting scheme of 75% to the MCQ component and 25% to the CDM section. A summary of the seven IRT calibrations that were carried out with this MCCQEI data set are summarized in Table 1.
Summary of all calibrations
We first examined the usefulness of each IRT model and calibration design by assessing the fit of each approach to the item response matrix. Both BILOG-MG 3 and PARSCALE 4 report a chi-square fit statistic in their output. This fit statistic is based on the difference between IRT model-based probabilities and observed-score proportions at each ability level. Large residuals (poor model fit) result in larger chi-square values. It is nonetheless important to underscore that Type I error rates for chi-square distributed statistics are inflated with large sample sizes. Consequently, we selected a nominal type I error rate of 0.01 as being indicative of misfit.
Next, correlations between the ability estimates were compared. The 7 IRT-based ability estimates were compared to the composite scores that were actually reported to candidates and computed using the current scoring approach. We then investigated the consistency of pass-fail decisions based on the 7 IRT abilities via-à-vis the actual decision reported using the current scoring model. A cut-score of ability estimate (θ)= -0.88 (previous MCQ cut-score) was used to signify a “pass.” In addition, decision inconsistencies were also summarized, e.g., a candidate fails based on an IRT ability estimate but actually passed using the current scoring approach. At the time this study was conducted, the passing rate for the MCCQEI had historically been about 85% for first-time test-takers. Finally, expected true scores for each component of the examination (MCQs and CDM questions) were computed for the 4 dichotomous IRT calibrations as a means of further informing the nature of the MCCQEI composite. Low correlations between the CDM and MCQ components would suggest that each section of the MCCQEI is targeting a dimensionally distinct construct. Conversely, high correlations would indicate that both components are tapping into a similar construct or composite.
Go to : 
Fit statistic results for the seven IRT calibrations are summarized in Table 2. Using a nominal Type I error rate of 0.01, the 2-PL dichotomous calibrations appeared to provide a slightly better fit of the item response matrix than the corresponding 1-PL model runs. Anchored vs. concurrent designs seemed to have little effect on findings for the dichotomous calibrations. The 2-PL model had identical numbers of items with chi-square values at or below a Type I error rate of 0.01 (83/3,499 or 0.02). However, the anchored 2-PL calibration seemed to provide a slightly worse fit of CDM questions, as evidenced by the higher proportion of items with chi-square values at or below a Type I error rate of 0.01 (0.06 or 6% of CDM questions). Ultimately, at the overall examination level, the proportion of MCCQEI items for which a given model (1-PL or 2-PL) did not fit ranged from 0.02 (both 2-PL calibrations) to 0.14 (1-PL anchored calibration). Misfit of the models was worse for CDM questions, especially within the 1-PL framework, where 0.27 or more of the questions were problematic, from a fit perspective.
Dichotomous item response theory (IRT) calibration fit statistics
While the dichotomous fit statistics were reasonable, the polytomous fit statistics were comparatively quite poor. In all 3 models, whether the MCQs were either anchored or concurrently run with the CDM cases, results suggest very poor fit of the models. The best fitting calibration/IRT model was the anchored GPCM/ CDM run which resulted in about 15% of the items for which the models did not fit (Table 3).
Next, the abilities estimated from each of the 7 IRT-based calibrations were compared to each other as well as to the actual MCCQEI scores reported to candidates. These correlations are provided in Table 4. All IRT abilities estimated from dichotomous calibration designs correlated very highly with each other. For example, the correlation between ability estimates from the concurrent 1-PL and 2-PL runs was equal to about 0.98. Calibration design (anchored or concurrent) seemed to have little effect as abilities estimated from the 1-PL concurrent and the 1-PL anchored runs correlated nearly perfectly (0.99). However, this is not consistently the case when comparing the latter abilities to those obtained from mixed item format IRT calibrations. The concurrent mixed format 2-PL GRM based abilities correlated highly with abilities estimated in the dichotomous calibrations (0.97 to 0.99). However, the anchored polytomous calibrations clearly differed from all of the other designs. Correlations between abilities estimated from the anchored mixed format calibrations and all others ranged from 0.74 to 0.78 (0.99 with each other). Thus, while abilities estimated from anchored mixed item format IRT calibrations were consistent (whether CDM case score parameters were based on the GRM or GPCM model), they diverged quite noticeably from the other ability estimates in the study.
Item response theory-based ability estimates and the Medical Council of Canada's Qualifying Examination Part I reported z-score correlations
More importantly, the correlation between most IRT-based abilities and actual MCCQEI z-scores for our cohort correlated very highly (Table 3). These correlations were near or exceeded 0.90 for all calibration designs, except the 2 anchored mixed item format anchored calibrations (about 0.70). These results are consistent with some of the misfit findings previously reported for the latter 2 calibrations. It is important to re-iterate that the previously reported z-score was not a gold standard per se, as it was based on real data and as such the true ability level of candidates was unknown. Nonetheless, calibrations that yield ability estimates which closely resemble past practices are desirable as rank ordering of candidate abilities is generally preserved from the initial reporting.
Given that the MCCQEI is a criterion-referenced examination, a major concern of the present study was to assess how consistently we are categorizing MCCQEI candidates based on both their IRT abilities and the previously reported z-score. Fig. 2 displays the pass-fail rates for each of the seven IRT-based calibration designs and for the reported z-scores for this group of 8,213 first time test-takers on 2010-2011 administrations of the MCCQEI. Again, the previous cut-score in place for the MCCQEI MCQ component (θ> = -0.88) was used to determine P/F status for each of the IRT ability estimates. Ultimately, IRT-based pass-fail rates were extremely similar, not only across calibration designs and methods, but also with regard to the actual reported decisions to candidates. The largest difference noted in pass rates was 4.78%, which occurred between the mixed format concurrent 2-PL-GRM (pass rate= 80.43%) and the dichotomous anchored 1-PL calibrations (pass rate= 85.21%). Comparing IRT-based pass-fail rates to z-score (reported) derived values, the largest difference was 4.52% and also occurred with the mixed format 2-PL-GRM concurrent calibration.
In addition to computing overall pass/fail rates by method, decision consistency as well as “false negative” and “false positive” rates were also examined. Table 5 displays the decision consistency, false positive and false negative rates for all seven calibrations. It is important to once more point out that real data were analyzed in this study and as such, true mastery level of candidates is unknown. For the purpose of our investigation, a false positive was defined as a candidate who actually passed the MCCQEI but would fail based on a given IRT ability estimate. Conversely, a false negative decision would correspond to the instance where a candidate actually failed the MCCQEI but would have passed based on a given IRT ability estimate. As shown in Table 5, the consistency in pass-fail decisions was very high in nearly all calibration designs (P> 0.95). Kappa coefficient values, outlining consistency above and beyond chance agreement, are presented in parentheses. All kappa coefficients are indicative of very strong agreement or consistency in decisions [3]. Not surprisingly, given correlation results previously reported, decision consistency with reported MCCQEI z-scores was the lowest for mixed format IRT-based anchored calibrations (still over 0.85). It is important to note that the percentage of examinees in the “decision area” (with 1 SE around the cut score) only accounts for a small fraction of the overall population, i.e., 84.95% of the candidates passing. Therefore, only a small percentage of the failures/passes are in the vicinity of the cut-score. This is typical of certification and licensure examinations, where a large proportion of candidates typically pass on their 1st or 2nd attempt especially those trained in Canada, in this instance. In the majority of the IRT-based calibrations, the “false positive” rate was slightly higher than the proportion of false negatives. This was more prominent with the concurrent calibration designs. The concurrent 2-PL-GRM calibration decision inconsistencies occurred as “false positives” in virtually all instances.
Decision classification and false positives and false negatives
The last analysis examined the expected true scores generated from the estimated θs and item parameters. Overall, the correlations for all the dichotomous runs were extremely similar ranging from 0.77 to 0.81. This suggests that MCQ and CDM components of the MCCQEI share about 60% of score variance. These high correlations suggest that the MCQ and CDM components might be tapping into the same dimension or composite. This, in turn, raises the question of whether CDMs are contributing something unique to the measurement process above and beyond what MCQs are targeting. This issue falls beyond the bounds of the present study but merits further research and consideration.
Go to : 
Our investigation had 2 primary research questions. First, what IRT model and calibration design might be acceptable to use to estimate an overall MCCQEI composite score? The results seem to suggest that there are small differences between the 7 calibrations that were examined in our research. Overall, irrespective of design, a 2-PL IRT model seemed to most accurately capture the performance of candidates on the entire MCCQEI examination and also provided the best fit of the item response matrix. All 3 mixed format IRT calibrations yielded very poor fit of the item response matrix (with respect to the polytomous calibration of CDM cases). Additionally, convergence issues were also quite troublesome with all of the IRT-based mixed format calibrations. Indeed, 100 items had to be manually removed from the polytomous IRT runs to ensure convergence. The latter process seems counter-intuitive to the need to further automate the scoring process. Collapsing across categories to reduce the sparseness of some categories might improve the polytomous IRT calibration portion in the mixed format calibrations. Some CDM case score categories contained very few candidates which could at least partially account for the poor results noted in the mixed format IRT calibrations. However, as previously noted, collapsing across categories further detracts from the desired automation of the scoring processes. Overall, despite their promise, more complex mixed calibration designs added little to simpler dichotomous IRT calibrations, in regard to both correlation with reported MCCQEI scores and decision consistency. It is perhaps not surprising to note that simple dichotomous IRT calibrations of CDM questions worked as well as more complex mixed item format estimations given that 2/3 of CDM questions are, de facto, dichotomous items (c.f. figure 1). Furthermore, nearly 60% of CDM cases were also dichotomous in nature. Thus, accounting for the polytomous nature of CDM cases was beneficial for only 40% of the cases and less than 35% of CDM questions.
The second primary question was “What is the correlation between between MCQ and CDM question-based expected true-scores?” It was interesting to note the high degree of correlation near 0.80. This would seem to suggest that CDMs, in their current form, are only minimally contributing to the measurement of candidate abilities within a MCCQEI framework. Alternatively, it is possible that MCCQEI MCQs have evolved in form and are actually also tapping into the same key features that are at the heart of CDM questions and cases. This is a question that merits further study by more formally modeling the underlying structure of the MCCQEI using confirmatory factor analysis.
In conclusion, our research suggests that simpler calibration designs with dichotomized items (both MCQs and CDM questions) should be implemented. The dichotomous calibrations provided better fit of the item response matrix than more complex, polytomous calibrations. Furthermore, dichotomous IRT calibration designs are much simpler in nature and easier to implement in a continuous testing framework that mixed item procedures. The latter advantages would also ensure that overall MCCQEI scores could be estimated in a nearly on the fly capacity which would permit more frequent test administrations.
Go to : 
References
1. Zimowski M, Muraki E, Mislevy R, Bock D. BILOG-MG 3. Multiple-group IRT analysis and test maintenance for binary items. Chicago (IL): Scientific Software International, Inc;2003.
2. Muraki E. PARSCALE 4: IRT based test scoring and item analysis for graded items and rating scales. Chicago (IL): Scientific Software International, Inc;2003.
Go to : 




 PDF
PDF Citation
Citation Print
Print




 XML Download
XML Download