With the development of radiation therapy technology, intensity-modulated radiation therapy (IMRT) and volumetric modulated radiation therapy (VMAT) are being widely used in various cancer treatments [
1-
4]. They can modulate fluence maps by using the multi-leaf collimator (MLC) to deliver high-dose radiation to treatment targets while delivering minimal dose of radiation to surrounding normal organs [
5]. To deliver optimized dose distribution to patients, fluence complexity must be improved, and many MLC movements are required for its implementation. As such, the MLC is a critical factor in radiation therapy.
The head scatter factor (S
c) is the relative ratio of all scattered radiation amounts from the head of the linear accelerator (linac). According to the American Association of Physicists in Medicine (AAPM) Task Group (TG)-74 report, the main causes of scattered radiation include the primary collimator, flattening filter, jaw, and MLCs [
6]. The AAPM TG-74 report has mentioned that scattered radiation by the MLC is no longer negligible as IMRT and VMAT use several small and irregular MLC fields [
6]. This led to the increased importance of scattered radiation from the MLC, and research was needed accordingly. Nevertheless, previous studies have developed models that did not consider scattered radiation from MLCs; these models were dual- and three-source models in which S
c is calculated by measuring the area of the model using detector’s eye view (DEV) [
7-
9]. When the MLC is located in a specific area as shown in
Fig. 1a, it is exposed to the radiation field and creates scattered radiation; however, it is not considered in DEV; thus, it does not affect the S
c calculation. Only when the MLCs enter the DEV area (
Fig. 1b), it can affect the S
c calculation. The MLC cannot be considered as present in region “a” of
Fig. 1c (the region where the MLC-defined square field size is from 8×8 to 15×15 cm
2 after the jaw-defined field size is fixed to 15×15 cm
2); thus, the S
c value in the field where the scattered radiation from MLCs is not considered is calculated similarly, resulting in a difference in the measured S
c value. In the “b” region (the region where the MLC-defined square field size is 4×4 to 8×8 cm
2 after the jaw-defined field size is fixed to 15×15 cm
2), the position of the MLC affects the DEV; thus, the calculated S
c value decreases as the field size decreases. In terms of area “a,” it is a very small difference between the calculated and measured S
c values, but in the case of IMRT or VMAT, which use hundreds of segments and control points, the combined difference can be large. Previously, we have developed an additional model that can consider scattered radiation from the MLCs [
10]. A model for considering scattered radiation from MLCs was located at the MLC location in the linac. The model was developed including line and area sources with scatter interface which was used for determining affected and unaffected areas. Details for scatter interface have been mentioned in the previous study [
10]. This model has been verified using a 6 MV photon beam. The results showed that the model was more accurate than the existing model, and particularly, the accuracy increased for very small and irregular fields. For this developed model, the accuracy of the independent verification program could be improved, and a more accurate pretreatment quality management evaluation was enabled.
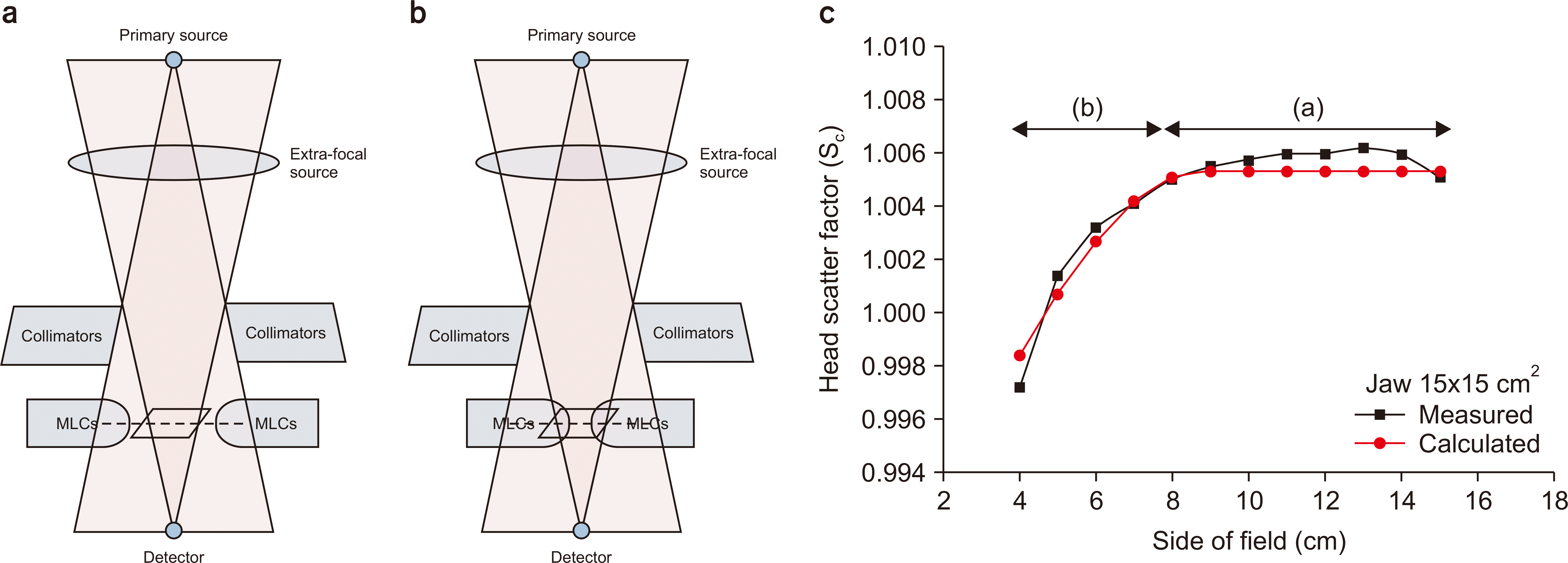 | Fig. 1Schematics of the geometrical relationship between the jaws and multi-leaf collimators (MLCs) in terms of the beam’s eye view, detector’s eye view, and scatter interface for (a) unaffected area, (b) affected area, and (c) head scatter factor (Sc) as a function of the MLC-defined square field size ranging from 4×4 to 15×15 cm2 at a fixed jaw setting of 15×15 cm2. The calculated Sc values are derived from the dual-source model. 
|
The unflattened filter (FFF) photon beam is a photon beam from which the flattened filter has been removed in the linac. For small fields, it has radiation quality and profiles similar to those of the flattened filter (FF) but has the advantage of rapidly ending the radiation treatment when dose rates increase by 2–4 times. As the demand for stereotactic ablative radiotherapy (SABR) increased, the use of unflattened filter photon beams also increased. The MLC models developed in the previous studies have not yet been verified for unflattened filter photon beams. When one of the most important factors of scattered radiation, the flattening filter, is removed, it is expected to have a significant influence on the model. Therefore, this study aims to verify the developed model for the unflattened filter photon beam.





 PDF
PDF Citation
Citation Print
Print



 XML Download
XML Download