2. Seong SC, Kim YY, Khang YH, Heon Park J, Kang HJ, Lee H, et al. Data resource profile: the national health information database of the national health insurance service in South Korea. Int J Epidemiol. 2017; 46(3):799–800. PMID:
27794523.
3. Bahk J, Kim YY, Kang HY, Lee J, Kim I, Lee J, et al. Using the National Health Information Database of the National Health Insurance Service in Korea for monitoring mortality and life expectancy at national and local levels. J Korean Med Sci. 2017; 32(11):1764–1770. PMID:
28960027.

4. Kim I, Lim HK, Kang HY, Khang YH. Comparison of three small-area mortality metrics according to urbanity in Korea: the standardized mortality ratio, comparative mortality figure, and life expectancy. Popul Health Metr. 2020; 18(1):3. PMID:
32620133.

5. Lim D, Bahk J, Ock M, Kim I, Kang HY, Kim YY, et al. Income-related inequality in quality-adjusted life expectancy in Korea at the national and district levels. Health Qual Life Outcomes. 2020; 18(1):45. PMID:
32103763.

6. Bahk J, Kang HY, Khang YH. Life expectancy and inequalities therein by income from 2016 to 2018 across the 253 electoral constituencies of the National Assembly of the Republic of Korea. J Prev Med Public Health. 2020; 53(2):143–148.
7. Khang YH, Lim D, Bahk J, Kim I, Kang HY, Chang Y, et al. A publicly well-accepted measure versus an academically desirable measure of health inequality: cross-sectional comparison of the difference between income quintiles with the slope index of inequality. BMJ Open. 2019; 9(6):e028687.

8. Kim I, Bahk J, Yun SC, Khang YH. Income gaps in self-rated poor health and its association with life expectancy in 245 districts of Korea. Epidemiol Health. 2017; 39:e2017011. PMID:
28330335.

9. Eayres D, Williams ES. Evaluation of methodologies for small area life expectancy estimation. J Epidemiol Community Health. 2004; 58(3):243–249. PMID:
14966240.

10. Bennett JE, Li G, Foreman K, Best N, Kontis V, Pearson C, et al. The future of life expectancy and life expectancy inequalities in England and Wales: Bayesian spatiotemporal forecasting. Lancet. 2015; 386(9989):163–170. PMID:
25935825.

11. Bennett JE, Pearson-Stuttard J, Kontis V, Capewell S, Wolfe I, Ezzati M. Contributions of diseases and injuries to widening life expectancy inequalities in England from 2001 to 2016: a population-based analysis of vital registration data. Lancet Public Health. 2018; 3(12):e586–97. PMID:
30473483.

12. Dwyer-Lindgren L, Bertozzi-Villa A, Stubbs RW, Morozoff C, Kutz MJ, Huynh C, et al. US county-level trends in mortality rates for major causes of death, 1980–2014. JAMA. 2016; 316(22):2385–2401. PMID:
27959996.

13. Dwyer-Lindgren L, Stubbs RW, Bertozzi-Villa A, Morozoff C, Callender C, Finegold SB, et al. Variation in life expectancy and mortality by cause among neighbourhoods in King County, WA, USA, 1990–2014: a census tract-level analysis for the Global Burden of Disease Study 2015. Lancet Public Health. 2017; 2(9):e400–10. PMID:
29253411.

14. Dwyer-Lindgren L, Bertozzi-Villa A, Stubbs RW, Morozoff C, Mackenbach JP, van Lenthe FJ, et al. Inequalities in life expectancy among US Counties, 1980 to 2014: temporal trends and key drivers. JAMA Intern Med. 2017; 177(7):1003–1011. PMID:
28492829.
15. Moran PA. Notes on continuous stochastic phenomena. Biometrika. 1950; 37(1-2):17–23. PMID:
15420245.

16. Leroux BG, Lei X, Breslow N. Estimation of disease rates in small areas: a new mixed model for spatial dependence. Statistical Models in Epidemiology, the Environment, and Clinical Trials. New York, NY: Springer-Verlag;2000. p. 179–191.
17. Knorr-Held L. Bayesian modelling of inseparable space-time variation in disease risk. Stat Med. 2000; 19(17-18):2555–2567. PMID:
10960871.

18. Thatcher AR, Kannisto V, Vaupel JW. The Force of Mortality at Ages 80 to 120. Odense, Denmark: Odense University Press;1998.
19. Khang YH, Hwang IA, Yun SC, Lee MS, Lee SI, Jo MW, et al. Census population vs. registration population: which population denominator should be used to calculate geographical mortality. J Prev Med Public Health. 2005; 38(2):147–153. PMID:
16315751.
21. Choi MH, Yoon TH. Trends in amenable mortality to health care across the districts in Korea from 1993 to 2013. J Crit Soc Welfare. 2015; (49): 404– 432.
22. Khang YH. Monthly Community Health Report. Geographic health inequalities: time trends in mortality indicators and future research agenda. Updated October 2019. Accessed March 20, 2020.
https://chs.cdc.go.kr/chs/hd/hdMain.do.
23. Khang YH, Bahk J, Lim D, Kang HY, Lim HK, Kim YY, et al. Trends in inequality in life expectancy at birth between 2004 and 2017 and projections for 2030 in Korea: multiyear cross-sectional differences by income from national health insurance data. BMJ Open. 2019; 9(7):e030683.

24. Bahk J, Lynch JW, Khang YH. Forty years of economic growth and plummeting mortality: the mortality experience of the poorly educated in South Korea. J Epidemiol Community Health. 2017; 71(3):282–288. PMID:
27707841.

25. Son M, Cho Y, Oh J, Kawachi I, Yi J, Kwon S. Social inequalities in life expectancy and mortality during the transition period of economic crisis (1993–2010) in Korea. Int J Equity Health. 2012; 11(1):71. PMID:
23171369.

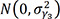 and N(0, ?2γ5)
and N(0, ?2γ5)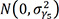 , respectively. These random effects allow for non-linear region-level deviations in the year and age group trends that are not captured by other trend components (i.e., linear deviations are accounted for by γ2,i and γ4,i). γ6,ta was assumed to follow a normal distribution, with the precision matrix specified as the Kronecker product of the structure matrices using a first-order random walk for each of year and age group (i.e., a type IV interaction in the Knorr-Held classification17), which allows for simultaneous smoothing over year and age groups. logGamma (1, 0.001) hyper-priors were specified for the logarithm of the precision of each random effect and normal (0, 1000) hyper-priors were used for the common intercept and slope.
, respectively. These random effects allow for non-linear region-level deviations in the year and age group trends that are not captured by other trend components (i.e., linear deviations are accounted for by γ2,i and γ4,i). γ6,ta was assumed to follow a normal distribution, with the precision matrix specified as the Kronecker product of the structure matrices using a first-order random walk for each of year and age group (i.e., a type IV interaction in the Knorr-Held classification17), which allows for simultaneous smoothing over year and age groups. logGamma (1, 0.001) hyper-priors were specified for the logarithm of the precision of each random effect and normal (0, 1000) hyper-priors were used for the common intercept and slope.




 PDF
PDF Citation
Citation Print
Print



 XML Download
XML Download