Abstract
Background
The selection of statistical analysis methods in research is a critical and nuanced task that requires a scientific and rational approach. Aligning the chosen method with the specifics of the research design and hypothesis is paramount, as it can significantly impact the reliability and quality of the research outcomes.
Methods
This study explores a comprehensive guideline for systematically choosing appropriate statistical analysis methods, with a particular focus on the statistical hypothesis testing stage and categorization of variables. By providing a detailed examination of these aspects, this study aims to provide researchers with a solid foundation for informed methodological decision making. Moving beyond theoretical considerations, this study delves into the practical realm by examining the null and alternative hypotheses tailored to specific statistical methods of analysis. The dynamic relationship between these hypotheses and statistical methods is thoroughly explored, and a carefully crafted flowchart for selecting the statistical analysis method is proposed.
Results
Based on the flowchart, we examined whether exemplary research papers appropriately used statistical methods that align with the variables chosen and hypotheses built for the research. This iterative process ensures the adaptability and relevance of this flowchart across diverse research contexts, contributing to both theoretical insights and tangible tools for methodological decision-making.
Conclusions
This study emphasizes the importance of a scientific and rational approach for the selection of statistical analysis methods. By providing comprehensive guidelines, insights into the null and alternative hypotheses, and a practical flowchart, this study aims to empower researchers and enhance the overall quality and reliability of scientific studies.
The nuanced process of selecting appropriate statistical analysis methods has emerged as a pivotal and multifaceted challenge in navigating the dynamic and ever-evolving landscape of modern scientific research. The proliferation of data and increasing complexity of research questions highlight the need for a thorough and comprehensive understanding of statistical methodology. At the heart of this complex effort is the recognition that statistical analyses play a central role in shaping and defining the integrity and interpretability of research results.
Choosing the appropriate statistical analysis method is not a one-size-fits-all task. Rather, it is a dynamic process influenced by the complex interactions between different datasets and the complexities inherent in the research hypothesis. As researchers grapple with a wide range of methodological choices, the importance of each decision becomes increasingly clear and the far-reaching implications for the validity and reliability of research findings grow. The multifaceted nature of statistical methodology becomes apparent when we consider the number of variables that are more than simple numbers and the complexities inherent in the experimental design, sample characteristics, and underlying assumptions of each statistical approach. Each of these factors contributes to the complex decision-making process that researchers must navigate, requiring a nuanced understanding and careful consideration of the unique needs that arise in each research endeavor. The interdependence of the data and research hypotheses further complicates this situation. A deep understanding of statistical analysis tools and a keen understanding of how these tools interact with specific research questions are therefore essential.
As statistical analysis methods and research hypotheses interact, the chosen statistical approach must accurately reflect the characteristics of the data and objectives of the study. In response to this complexity, researchers must develop a methodological sophistication that extends beyond the simple application of statistical techniques. Rather, a keen awareness of the assumptions, hypotheses, strengths, and limitations inherent to each method is necessary. Navigating this environment therefore involves not only choosing a statistical tool but also understanding why a particular tool is appropriate for a given situation. Efforts to guide researchers through this complex process require thus more than an explanation of the statistical techniques.
This study presents a detailed description of the sequential steps for statistical hypothesis testing. It also includes an explanation of the variable types, an exploration of different statistical hypothesis tests, and a careful examination of important considerations when choosing a statistical analysis method. We also introduce a structured flowchart designed to serve as a practical tool for researchers to navigate through the various methodological options.
The final goal of this study is to improve methodological precision by facilitating researchers’ understanding of a comprehensive algorithm for choosing statistical methods based on the variables of interest and research hypotheses. By exploring the complexities of statistical analysis, we aim to provide researchers with the insights and resources needed to delve into their scientific inquiries with confidence, methodological rigor, and an unwavering commitment to advancing knowledge.
Statistical hypothesis testing is a structured process involving five key steps [1]. First, the hypothesis is formulated, then the significance level is established, the test statistic is calculated, the rejection area or significance probability (P value) is determined, and conclusions are drawn. In the conclusion stage, if the test statistic falls outside the rejection area, or the P value is greater than the predetermined significance level, “the null hypothesis cannot be rejected at the predetermined significance level.” Conversely, if the test statistic falls within the rejection area, or if the P value is less than the predetermined significance level, “the null hypothesis is rejected at the significance level.” In this case, conclusions are drawn and interpreted in alignment with the alternative hypothesis rather than the null hypothesis. For example, in a statistical hypothesis test where the significance level is set at 0.05 and the calculated significance probability is 0.002, the null hypothesis is rejected. Similarly, in a statistical hypothesis test where the significance level is set at 0.1 and the calculated significance probability is 0.07, the null hypothesis is also rejected. The conclusion is based on the content of the alternative hypothesis. This process provides a systematic framework for researchers to rigorously evaluate hypotheses and draw meaningful conclusions based on statistical evidence. The decisive stages of hypothesis testing serve as a robust foundation for deriving insights into the underlying dynamics of null and alternative hypotheses and contribute to the integrity and reliability of the research outcomes.
As the word suggests, a variable is a “changeable number.” Variables with their inherent property of variability can be investigated through measurements or observations, manifesting diverse values based on the object under scrutiny. Examples of variables include anthropometric measures such as height, demographic factors such as age, and health indicators such as body mass index (BMI). These diverse entities allow researchers to capture and quantify essential characteristics in their studies. Broadly, variables fall into two primary categories: categorical (qualitative) and quantitative. Categorical variables encapsulate characteristics that resist straightforward quantification and further branch into two subtypes: nominal and ordinal. Nominal variables serve as descriptors representing names, labels, or categories without any inherent order. A classic example is sex, in which the categories of male and female do not have a natural ranking. On the other hand, ordinal variables introduce an element of order, defining values based on a ranking system between different categories. The quintessential example is assessing the satisfaction level using a Likert-type scale (e.g., “very dissatisfied,” “dissatisfied,” “neither dissatisfied nor satisfied,” “satisfied,” and “very satisfied”).
By contrast, quantitative variables denote characteristics that can be precisely quantified and expressed as numerical values. A quantitative variable is further subdivided into continuous and discrete variables. Continuous variables can assume an infinite number of real values within a defined interval, offering a nuanced representation of the attributes. Examples include age, which captures a spectrum of real values, and height, which spans a continuous range of measurements. In contrast, discrete variables can only take a finite set of real values within a given range. An example is the number of children, where the possible values are limited to zero and positive integers (e.g., 0, 1, 2, etc.).
In essence, variables, as discerned from their names, embody a concept of change that can be expressed numerically. This intricate tapestry of variability allows for a nuanced understanding of data in research and analysis.
As mentioned previously, determining the statistical hypothesis testing method is contingent on the hypothesis established for the analysis. In other words, hypotheses are formulated in alignment with the selected statistical analysis method. In this section, we delve deeper into specific hypotheses associated with the various statistical analysis methods. Table 1 summarizes the types of variables and the null and alternative hypotheses for the various statistical analysis methods. In this study, various statistical analysis methods are discussed, including normality test, one-group mean and independent two-group mean difference test, dependent or before-and-after group mean difference test, one-way analysis of variance (ANOVA), repeated-measures ANOVA, chi-square test, Fisher’s exact test, correlation analysis, linear regression analysis, and logistic regression analysis.
We also examine the null and alternative hypotheses in detail and show how to correctly interpret the result when the null hypothesis is rejected. To determine whether the null hypothesis should be rejected, the results obtained from the statistical analysis are compared with predetermined significance levels. When the null hypothesis is rejected, the observed data provides sufficient evidence to contradict the notion that no effect or difference exists. In a two-tailed test, rejection area of the null hypothesis implies that the observed outcome falls on either the extreme right or left tail of the distribution, suggesting a statistically significant deviation from the expected outcome. Understanding the nuances of null and alternative hypotheses and the outcomes of their testing is pivotal for researchers and practitioners to draw meaningful conclusions from statistical analyses. This section demystifies these concepts and offers insights into the intricacies of hypothesis testing across a spectrum of statistical methods.
The normality test is a statistical method used to test whether the collected data follows a normal distribution or satisfies normality [2]. The null hypothesis states that “the data follows a normal distribution” and the alternative hypothesis states that “the data does not follow a normal distribution.” If the null hypothesis is rejected, the conclusion is that “the data cannot be said to statistically follow a normal distribution under significance level,” and thus the data does not follow a normal distribution. If the data satisfies normality, the data should be analyzed using a parametric approach and presented with statistics, such as the mean, standard deviation, and confidence interval. If the data does not satisfy normality, the data should be analyzed using a nonparametric approach and presented with statistics, such as the median, quartiles, and interquartile range [2,3].
The types of t-tests include the one-sample t-test (one-group mean difference test), two-sample t-test (independent two-group mean difference test), and paired t-test (dependent or before-and-after group mean difference test) [4,5]. The one-sample t-test is a statistical hypothesis-testing method used to assess whether the average of a group is the same or different from a specific value. The null hypothesis states that “the average of the group is equal to the specific value” and the alternative hypothesis states that “the average of the group is different from the specific value.” If the null hypothesis is rejected, the conclusion is that “the average of the group cannot be statistically equal to the specific value under the significance level,” and the average of the group can be judged to be different from the specific value. The two-sample t-test is a statistical hypothesis-testing method used to test whether the averages of two independent groups are the same or different. The null hypothesis states that “the averages of group A and group B are the same” and the alternative hypothesis states that “the averages of group A and group B are different.” If the null hypothesis is rejected, the conclusion is that “the averages of group A and group B cannot be said to be statistically the same under the significance level,” and it can be determined that the averages of group A and group B are different. The paired t-test is a statistical hypothesis-testing method used to assess whether the average difference between the dependent or before-and-after groups is zero or not. Data from the two dependent or before-and-after groups is created when two measurements are taken from the same subject at different times. An initial measurement is made, and then the measurement is taken again after some type of intervention, such as an educational program, training program, surgery, or medication. Therefore, the purpose of this type of study is to determine whether an intervention performed between two measurements is effective, and the amount of change must be calculated for each subject to determine whether the average is zero. The null hypothesis states that “the average of the difference between the two dependent or before-and-after groups is equal to zero” and the alternative hypothesis states that “the average of the difference between the two dependent or before-and-after groups is different from zero.” If the null hypothesis is rejected, the conclusion is that “the average of the difference between the two dependent or before-and-after groups cannot be said to be statistically equal to zero under the significance level,” and the average of the difference between the two dependent or before-and-after groups can be judged to be different from zero. The specific type of intervention performed between the two measurements can then be said to be statistically effective.
An ANOVA is a statistical hypothesis testing method used to determine whether the averages of three or more independent groups are the same [6]. If the averages of three independent groups are compared, the null hypothesis states that “all averages of groups A, B, and C are the same” and the alternative hypothesis is that “all averages of groups A, B, and C are not the same.” Importantly, the alternative hypothesis states that “they are not the same,” which is different from “they are all different.” Although the averages of all three groups may indeed be different, the phrase “not the same” can also mean that two of the three groups are the same and one group is different. Therefore, if the null hypothesis is rejected, a post-hoc analysis or multiple comparison should be conducted to examine the differences among the various cases that are “not the same” [7,8]. In addition, because the Bonferroni correction problem occurs when the same hypothesis is tested multiple times, investigators must consider that a type 1 error will occur to the extent that multiple comparisons are performed.
Additional expanded concepts of ANOVA include analysis of covariance (ANCOVA) and multivariate analysis of variance (MANOVA). ANCOVA is a method for testing the pure impact of an explanatory variable on a response variable by controlling for covariates that can affect the relationship between the explanatory and response variables. MANOVA is a method used to test the relationship between two or more response and explanatory variables. Multivariate analysis of covariance (MANCOVA) is the term used when covariates are considered in MANOVA. In this study, detailed information regarding the Bonferroni correction problem, ANCOVA, MANOVA, and MANCOVA is not provided.
A one-factor repeated-measures ANOVA is a statistical hypothesis testing method used for data measured three or more times to determine whether the averages for each measurement are the same. Repeated measurements generally refer to repeated measurements over time, but they may also depend on the location, such as the general ward, operating room, post-anesthetic care unit, and surgical intensive care unit. The point in time is the “one factor” measured repeatedly. If the averages of three repeated measurements are being compared, the null hypothesis states that “all averages in the first, second, and third measurements are the same” and the alternative hypothesis states that “all averages in the first, second, and third measurements are not the same.” As mentioned with one-way ANOVA, the alternative hypothesis for one-factor repeated-measures ANOVA states that the averages are “not the same”; therefore, if the null hypothesis is rejected, the individual cases that are “not the same” need to be further analyzed.
Two-factor repeated-measures ANOVA is a statistical hypothesis testing method used on data measured repeatedly three or more times for each group out of two or more groups. The repeatedly measured point in time is one factor and the group is another factor, so it is considered “two-factor.” In two-factor repeated-measures ANOVA, a total of three tests are performed [9]. First, whether the averages at each measured time point are the same or not is tested, ignoring the effect of the group (i.e., only differences in the test variable among the time points are tested). Second, whether the averages for each group are the same or not is tested, ignoring the effect of the time point (i.e., only differences in the test variable among the groups are tested). Finally, whether the patterns of changes in the test variable among the groups are the same or not among the time points is tested (i.e., the differences in the changes in the test variable among the time points and groups [interaction effects between time point factor and group factor] are tested.). If the research design uses a two-factor repeated-measures ANOVA, the primary goal is to see the pattern of change between groups as the time points change. If you are comparing the averages of three repeated measurements for two groups, the null hypothesis for the time points alone states that “all averages in the first, second, and third measurements are the same” and the alternative hypothesis states that “all averages in the first, second, and third measurements are not the same.” If the null hypothesis is rejected, differences among the many cases that are “not the same” need to be further analyzed. The null hypothesis for the group alone states that “the averages of the two groups are the same” and the alternative hypothesis states that “the averages of the two groups are not the same.” Lastly, the null hypothesis for the difference in the pattern of change between the two groups and among the three time points states that “the change patterns between the two groups are the same as time progresses from the first point to the third point,” and the alternative hypothesis is “the change patterns between the two groups are not the same as time progresses from the first point to the third point.” If the null hypothesis is rejected, it needs to be further evaluated between which time points the change patterns between the two groups exist.
The chi-square method can be used for a goodness-of-fit test, which is used to determine whether the observed frequency follows a specific distribution, and an independence or homogeneity test to determine whether two categorical variables are independent or homogeneous, respectively [10]. As an example of a goodness-of-fit test, data on the number of traffic accidents is collected each day from Monday to Friday, and researchers determine whether they occur equally on each day, following a specific distribution (Monday: Tuesday: Wednesday: Thursday: Friday = 1:1:1:1:1). The null hypothesis states that “the collected data follows a specific distribution” and the alternative hypothesis states that “the collected data does not follow a specific distribution.” If the null hypothesis is rejected, the conclusion is that “the data cannot be said to statistically follow a specific distribution under the significance level,” and it can be determined that the specified distribution is not followed.
Alternatively, an independence or homogeneity test can be conducted to examine whether there is a relationship between smoking and the development of lung cancer. The sentence “whether you smoke or not is independent of the incidence of lung cancer” has the same meaning as the sentence “the distribution of lung cancer in subjects who smoke and the distribution of lung cancer in subjects who do not smoke are the same.” However, whether a test is classified as an independence or homogeneity test depends on the topic of the research and the content of the data. The null hypothesis in the independence test states that “the relationship between the two categorical variables is independent” and the alternative hypothesis states that “the relationship between the two categorical variables is dependent.” If the null hypothesis is rejected, the conclusion is that “the relationship between the two categorical variables cannot be said to be statistically independent under the significance level,” and the relationship between the two categorical variables can be judged to be dependent. The null hypothesis in the homogeneity test states that “the distribution of categorical variable B according to categorical variable A is homogeneous” and the alternative hypothesis states that “the distribution of categorical variable B according to categorical variable A is not homogeneous.” If the null hypothesis is rejected, the conclusion is that “the distribution of categorical variable B according to categorical variable A cannot be said to be statistically homogeneous under the significance level,” and it can be determined that the distribution of categorical variable B according to categorical variable A is heterogeneous.
The Fisher’s exact test is an analysis method that identifies the relationship between two categorical variables in a 2 × 2 contingency table when the sample size is small. The conditions for performing the Fisher’s exact test [10] are as follows: 1) a 2 × 2 contingency table is required (i.e., both categorical variables must have two levels), 2) one cell must have an expected frequency < 5, and 3) the total number of study subjects or the sample size must be < 40. The Fisher’s exact test is performed when all three conditions are satisfied. If one of the conditions is not satisfied, the Fisher’s exact test should not be performed and the chi-square test should be performed instead.
Correlation analyses involve 1) calculating a correlation coefficient that measures the strength of the linear relationship between two variables and 2) testing the significance of the correlation coefficient to determine whether the calculated correlation coefficient is zero [11]. If the two variables being analyzed are ratio scales, Pearson’s correlation coefficient is calculated and if one of the two variables is a rank scale, Spearman’s correlation coefficient is calculated. The two correlation coefficients measure the strength of the linear relationship between two variables. Additionally, the closer to +1 the correlation coefficient, the stronger the positive linear relationship between the two variables, whereas the closer to -1 the correlation coefficient, the stronger the negative linear relationship. If the correlation coefficient is 0, no linear relationship is indicated. Therefore, a significance test must be performed to determine whether the calculated correlation coefficient is zero. The null hypothesis states that “the correlation coefficient is zero” and the alternative hypothesis states that “the correlation coefficient is not zero.” If the null hypothesis is rejected, the conclusion is that “the correlation coefficient cannot be said to be statistically zero under the significance level,” and a significant positive or negative linear correlation is indicated, depending on the sign of the correlation coefficient.
Linear regression is a statistical analysis method used to estimate a regression model that defines the linear relationship between one or more explanatory variable(s) and a quantitative response variable. Linear regression analyses involve the following: 1) the regression coefficient of each explanatory variable is estimated, 2) the regression model is tested on whether all estimated regression coefficients are equal to zero, 3) it is tested whether the regression coefficients of each explanatory variable are equal to zero, 4) the final regression model is built, and 5) the coefficient of determination (R2) is calculated to show how well the regression model explains the data used to build the model [12].
The null hypothesis for the significance test of the regression model states that “all regression coefficients are zero” and the alternative hypothesis states that “at least one regression coefficient is not zero.” If the null hypothesis is rejected, the conclusion is that “it cannot be stated that all the regression coefficients are zero under the significance level.” Because at least one regression coefficient is not zero, the estimated regression model shows a significant linear relationship between the response and explanatory variables. For testing the significance of the regression coefficient, the null hypothesis states that “the regression coefficient is zero” and the alternative hypothesis states that “the regression coefficient is not zero.” If the null hypothesis is rejected, the conclusion is that “the regression coefficient cannot be said to statistically be zero under the significance level.” Because the calculated regression coefficient is not zero, a 1-unit change in the explanatory variable results in the changes in the response variable by the value of the regression coefficient if the other explanatory variables are held constant.
Linear regression analyses must satisfy several assumptions in order to be performed. First, the distribution of the residuals must satisfy normality. Otherwise, a generalized linear model (GLM) should be conducted rather than a linear regression analysis. Second, the residuals must satisfy homoscedasticity. If the residuals do not satisfy homoscedasticity, the regression model needs to be modified by transforming the response variable to fulfill the homoscedasticity. Third, the residuals must satisfy independence. If the residuals do not satisfy independence, which indicates a dependent relationship between the residuals, a time-series regression analysis should be performed rather than a linear regression analysis. Fourth, linearity of the regression model must be satisfied. If linearity of the regression model is not satisfied, the explanatory or response variable must be transformed or the model must be reset such that linearity is satisfied. Finally, multicollinearity should not exist between the explanatory variables used in the linear regression model [13]. If multicollinearity does exist, variable selection methods such as stepwise selection, forward selection, and backward elimination should be used to modify the regression model. In summary, linear regression analyses must satisfy five assumptions: 1) normality of residuals, 2) homoscedasticity of residuals, 3) independence of residuals, 4) linearity of the model, and 5) absence of multicollinearity among the explanatory variables. If any of these assumptions are not satisfied, the linear regression model should not be accepted. Therefore, to create a reliable linear regression model, the following steps should be repeated until the five assumptions are met: 1) setting up a linear regression model, 2) assessing whether the five assumptions are met, and 3) modifying the linear regression model.
Linear regression analyses can be divided into simple and multiple linear regression analyses, depending on the number of explanatory variables. If the number of explanatory variables is only one, it is classified as a simple linear regression analysis, whereas if the number of explanatory variables is two or more, it is classified as a multiple linear regression analysis.
Logistic regression is a statistical analysis method used to estimate a regression model that defines the linear relationship between one or more explanatory variables and a log odds ratio (logit) of a categorical response variable [14]. Most concepts for logistic regression analyses are the same as those for linear regression analyses; however, since the response variable is a categorical rather than a quantitative variable, it is logit transformed. Therefore, rather than calculating the regression coefficient, as in the linear regression model, the odds ratio is calculated. Logistic regression analyses involve the following: 1) the odds ratios for each explanatory variable are estimated, 2) the significance of the logistic regression model is tested, and 3) the significance of the odds ratios for each explanatory variable is tested, 4) the final logistic regression model is constructed.
The null hypothesis in the significance test of the logistic regression model states that “all the odds ratios are equal to one” and the alternative hypothesis states that “at least one odds ratio is not one.” If the null hypothesis is rejected, the conclusion is that “all the odds ratios cannot be said to be statistically equal to one under the significance level.” Because at least one odds ratio is not one, the obtained logistic regression model is significant. For testing the significance of the odds ratio for each explanatory variable, the null hypothesis states that “the odds ratio is one” and the alternative hypothesis states that “the odds ratio is not one.” If the null hypothesis is rejected, the conclusion is that “the odds ratio cannot be said to statistically be one under the significance level.” Because the calculated odds ratio is not one, the relationship between the explanatory variable and the response variable can be explained as follows.
The odds ratio is interpreted differently depending on whether the explanatory variable used in the logistic regression analysis is a categorical or quantitative variable. If the explanatory variable is categorical, one level of the explanatory variable should become the reference, and the odds ratios to the other levels are calculated. For example, if the explanatory variable is sex, the levels of which are male (reference) and female, the odds ratio of females to males can be calculated. The odds ratio for male is 1, because male is used as the reference. Conversely, female can be used as the reference, in which case the odds ratio for female would be 1. The researcher can set the reference according to the research situation. Conversely, if the explanatory variable is quantitative, designating a reference is not necessary. In this case, a 1-unit increase in the explanatory variable increases the odds of the response variable by the odds ratio if the other explanatory variables are held constant (e.g., if the odds ratio of a quantitative explanatory variable is 1.2, 1-unit increase in the explanatory variable increases the odds ratio by 20%)
Similar to linear regression analyses, logistic regression analyses can be divided into simple and multiple logistic regression analyses, depending on the number of explanatory variables. If the number of explanatory variables is one, a simple logistic regression analysis is conducted, whereas if the number of explanatory variables is two or more, a multiple logistic regression analysis is conducted. Depending on the number of levels of the response variable, logistic regression analyses can be further divided into binary and multinomial. If the number of levels for the response variable is two, a binary logistic regression analysis is conducted, whereas if the number of levels for the response variable is three or more, a multinomial logistic regression analysis is conducted. Therefore, four logistic regression analysis divisions can be used according to the number of explanatory variables and the number of levels for the response variable as follows: 1) if the number of explanatory variables is one and the number of levels for the response variable is two, the classification is a simple binary logistic regression analysis; 2) if the number of explanatory variables is one and the number of levels for the response variable is three or more, the classification is a simple multinomial logistic regression analysis; 3) if the number of explanatory variables is two or more and the number of levels for the response variable is two, the classification is a multiple binary logistic regression analysis; and 4) if the number of explanatory variables is two or more and the number of levels for the response variable is three or more, the classification is a multiple multinomial logistic regression analysis. However, if the response variable is an ordinal variable, the word “multinomial” is changed to “ordinal” (Table 2).
Fig. 1 shows a flowchart designed to guide researchers in selecting the appropriate statistical analysis method. In the flowchart, the flowline represents the execution order of the process and the rectangular shape represents the proposed statistical analysis method. The diamond shapes represent a condition that, according to the investigator’s response (e.g., yes/no, quantitative/categorical, one/two, etc.), determines the direction of the pathway to follow.
The decision process begins from the black diamond located at the center, the condition for which is the type of response variable (categorical or quantitative). Proceeding along the pathway tailored to match the characteristics of each study and dataset will lead to the identification of the most suitable statistical analysis method. The recommended statistical analysis methods are encapsulated within rectangles on a gray background, each accompanied by a description of the corresponding statistics to be presented in the results. This visual aid serves as a navigational tool for simplified processes of selecting an appropriate statistical analysis method based on the context of the study and the unique properties of the data.
To demonstrate the appropriate use of the proposed flowchart, a few examples will be presented and the process described. First, we can consider the prospective randomized controlled trial conducted by Lee et al. [15] that examines whether intravenous patient-controlled analgesia or a continuous block prevents rebound pain following an infraclavicular brachial plexus block after distal radius fracture fixation. In this study, visual analog scale (VAS) scores and total opioid equivalent consumption were compared among three groups, each consisting of 22 patients (the brachial plexus block only, intravenous patient-controlled analgesia, and continuous block groups). Additionally, age (years), BMI (kg/m2), sex, American Society of Anesthesiologists (ASA) classification (1/2/3), and fracture type (A/B/C) were compared as baseline information. The statistical analysis section of this study states that the Kruskal-Wallis test was used to compare groups for age, BMI, VAS scores at each time point, and total opioid consumption. Fig. 2 illustrates the use of the flowchart presented in Fig. 1 (expressed by thick solid lines and black diamonds) to select the appropriate statistical analysis method for this study. First, as the response variables (age and BMI) are quantitative variables, the pathway from the starting (first) diamond to the right is indicated. For the second diamond, the explanatory variable (group with three levels [3 groups]) is a categorical variable, indicating the pathway to the left. For the third diamond, as there is only one explanatory variable, the pathway to the left is indicated. For the fourth diamond, the explanatory variable, group, has three categories, so the right pathway should be followed. For the fifth diamond, the groups are independent, so the left pathway is followed. For the sixth diamond, because normality is not satisfied, the path leading upward should be followed, finally indicating that the Kruskal-Wallis statistical analysis method should be used.
Additionally, the authors mention that the Fisher’s exact test was used for group comparisons of sex, ASA classification, and fracture type. Fig. 3 indicates, with thick solid lines and black diamonds, how the flowchart from Fig. 1 can be used to select this statistical analysis method. First, the response variable (sex) is a categorical variable, indicating the pathway from the starting diamond to the left. For the second diamond, the response variable has two categories (male/female), indicating the downward path. For the third diamond, the explanatory variable (group with three levels) is a categorical variable; thus, the path to the left should be followed. For the fourth diamond, there is one explanatory variable, so the path to the left is indicated. For the fifth diamond, the contingency table is 2 × 3 rather than 2 × 2; thus, the right pathway is followed, finally indicating that the chi-square test (not Fisher’s exact test) should be used for statistical analysis.
Next, the response variables (ASA classification and fracture type) are categorical variables; therefore, the pathway from the starting diamond to the left is indicated. For the second diamond, the response variables have three categories; thus, the upward path should be followed. For the third diamond, the explanatory variable (group) is a categorical variable, thus the left path is indicated. For the fourth diamond, the number of explanatory variables is one, so the left pathway is followed, finally indicating that the chi-square test should be used for statistical analysis. In the above cases, no thick solid lines and block diamonds were indicated.
Another example is the study entitled “neuromodulation of the median nerve in carpal tunnel syndrome, a single-blind, randomized controlled study,” published by Genç Perdecioğlu et al. [16]. In this study, the Boston Carpal Tunnel Syndrome Questionnaire (BCTQ) score was measured in 36 and 26 patients with carpal tunnel syndrome in the noninvasive pulsed radiofrequency and splinting (control) groups, respectively, at baseline, the 4th week, and the 8th week. The patients’ age (years), sex, and electroneuromyelography findings were compared as baseline data. In the statistical analysis section of this study, the authors indicate that the chi-square test was used for categorical variables and the t-test was used for quantitative variables. Fig. 4 illustrates how the flowchart from Fig. 1 could be used to select the statistical analysis method. First, the response variable (BCTQ score) is a quantitative variable, thus the path to the right of the starting diamond is indicated. For the second diamond, the explanatory variable (group with two levels) is categorical; thus, the left path is indicated. For the third diamond, the number of explanatory variables is one, indicating the left path. For the fourth diamond, the explanatory variable has two categories; thus, the left pathway is indicated. For the fifth diamond, the explanatory variables are independent; thus, the left pathway should be followed. For the sixth diamond, as normality is satisfied, the path to the left is followed, finally indicating that the two-sample t-test should be used for statistical analysis.
The authors also state that as the BCTQ was scored three times, a two-way repeated-measures ANOVA was used. Fig. 5 demonstrates how the flowchart from Fig. 1 could have been used to determine the statistical analysis method. First, the response variable (BCTQ score) is a quantitative variable, indicating the pathway to the right of the starting diamond. For the second diamond, the explanatory variable (group) is categorical; thus, the left path should be followed. For the third diamond, the number of explanatory variables is one, so the left pathway is indicated. For the fourth diamond, the number of explanatory variable categories is three; thus, the right pathway should be followed. For the fifth diamond, the explanatory variable is dependent, indicating the right path. For the sixth diamond, normality is satisfied, so the left pathway is indicated. For the seventh diamond, sphericity is satisfied, so the pathway to the left should be followed, finally indicating that the repeated-measures ANOVA statistical analysis method should be used.
In this study, we have delineated the precise formulations of the null and alternative hypotheses according to various statistical analysis methods. Emphasis was placed on critical considerations for the application and interpretation of these hypotheses. The systematic steps involved in statistical hypothesis testing, including the sequential processes of hypothesis formulation, establishment of the significance level, computation of test statistics, determination of the rejection area and significance probability, and drawing conclusive inferences, were discussed. The identification and characterization of different types of variables were explored to elucidate their distinctive features. This involved a detailed examination of the null and alternative hypotheses specific to commonly utilized statistical analysis methods, accompanied by a discussion of the essential precautions relevant for testing each statistical hypothesis. We also introduced a flowchart designed as a visual aid to facilitate the selection of the most suitable statistical analysis method. This innovative tool provides researchers with a structured path to explore various types of research data and serves as a comprehensive guideline for selecting statistical analysis methods.
It is hoped that this study will help researchers select appropriate statistical analysis methods and establish accurate hypotheses in statistical hypothesis testing.
Notes
Data Availability
The datasets generated and/or analyzed during the current study are available from the corresponding author upon reasonable request.
Author Contributions
Jonghae Kim (Conceptualization; Formal analysis; Methodology; Validation; Writing – review & editing)
Dong Hyuck Kim (Data curation; Methodology; Writing – review & editing)
Sang Gyu Kwak (Conceptualization; Data curation; Formal analysis; Investigation; Methodology; Writing – original draft)
References
1. Kwak S. Are only p-values less than 0.05 significant? A p-value greater than 0.05 is also significant! J Lipid Atheroscler. 2023; 12:89–95.
2. Kim TK, Park JH. More about the basic assumptions of t-test: normality and sample size. Korean J Anesthesiol. 2019; 72:331–5.
3. Nahm FS. Nonparametric statistical tests for the continuous data: the basic concept and the practical use. Korean J Anesthesiol. 2016; 69:8–14.
4. Casella G, Berger RL. Statistical inference. 2nd ed. Pacific Grove, Duxbury/Thomson Learning. 2002, pp 374-82.
5. Kim TK. T test as a parametric statistic. Korean J Anesthesiol. 2015; 68:540–6.
6. Pukelsheim F. Optimal design of experiments. Philadelphia, SIAM. 2006, pp 1-4.
7. Lee S, Lee DK. What is the proper way to apply the multiple comparison test? Korean J Anesthesiol. 2018; 71:353–60. Erratum in: Korean J Anesthesiol 2020; 73: 572.
8. Kim TK. Understanding one-way ANOVA using conceptual figures. Korean J Anesthesiol. 2017; 70:22–6.
9. Lee Y. What repeated measures analysis of variances really tells us. Korean J Anesthesiol. 2015; 68:340–5.
10. Agresti A. Categorical data analysis. 3rd ed. Hoboken, John Wiley & Sons. 2013, pp 90-3.
11. Kutner MH, Nachtsheim C, Neter J. Applied Linear Regression Models. 4th ed. New York, McGraw-Hill/Irwin. 2004, pp 78-87.
12. Lewis-Beck C, Lewis-Beck M. Applied regression: An introduction. 2nd ed. Thousand Oaks, Sage publications, Inc. 2015, pp 55-60.
13. Kim JH. Multicollinearity and misleading statistical results. Korean J Anesthesiol. 2019; 72:558–69.
14. Hosmer Jr DW, Lemeshow S, Sturdivant RX. Applied logistic regression. Hoboken, John Wiley & Sons. 2013, pp 1-10.
15. Lee JH, Kim HJ, Kim JK, Cheon S, Shin YH. Does intravenous patient-controlled analgesia or continuous block prevent rebound pain following infraclavicular brachial plexus block after distal radius fracture fixation? A prospective randomized controlled trial. Korean J Anesthesiol. 2023; 76:559–66.
16. Genç Perdecioğlu GR, Panpallı Ateş M, Yürük D, Akkaya ÖT. Neuromodulation of the median nerve in carpal tunnel syndrome, a single-blind, randomized controlled study. Korean J Pain. 2024; 37:34–40.
Fig. 1.
Flowchart for selecting the statistical analysis method. Expanded concepts of analysis of variance (ANOVA) include analysis of covariance (ANCOVA) and multivariate analysis of variance (MANOVA). ANCOVA is a method used to test the pure impact of an explanatory variable on a response variable by controlling for covariates that can affect the relationship between the explanatory and response variables. MANOVA is a method used to test the relationship between two or more response and explanatory variables. If covariates are considered in MANOVA, multivariate analysis of covariance (MANCOVA) is indicated. C: categorical, CC: correlation coefficient, CO: coefficient, Dep: dependent, EF: expected frequency, EV: explanatory variable, Ind: independent, IQR: interquartile range, M: mean, MCR: multiple comparison result, ME: median, N: number of subjects, N(EV): number of explanatory variables, NL(EV): number of levels for the explanatory variable, NL(RV): number of levels for the response variable, OR: odds ratio, Q: quantitative, Ref: reference, RV: response variable, SD: standard deviation, SMD: standardized mean difference, SMED: standardized median difference, w/: with, w/o: without. *Both the response variable and the explanatory variable should be the ratio scale. †At least one of the response variable and the explanatory variable is the rank scale. ‡C and Q mixed: explanatory variables have at least one categorical and one quantitative variable.
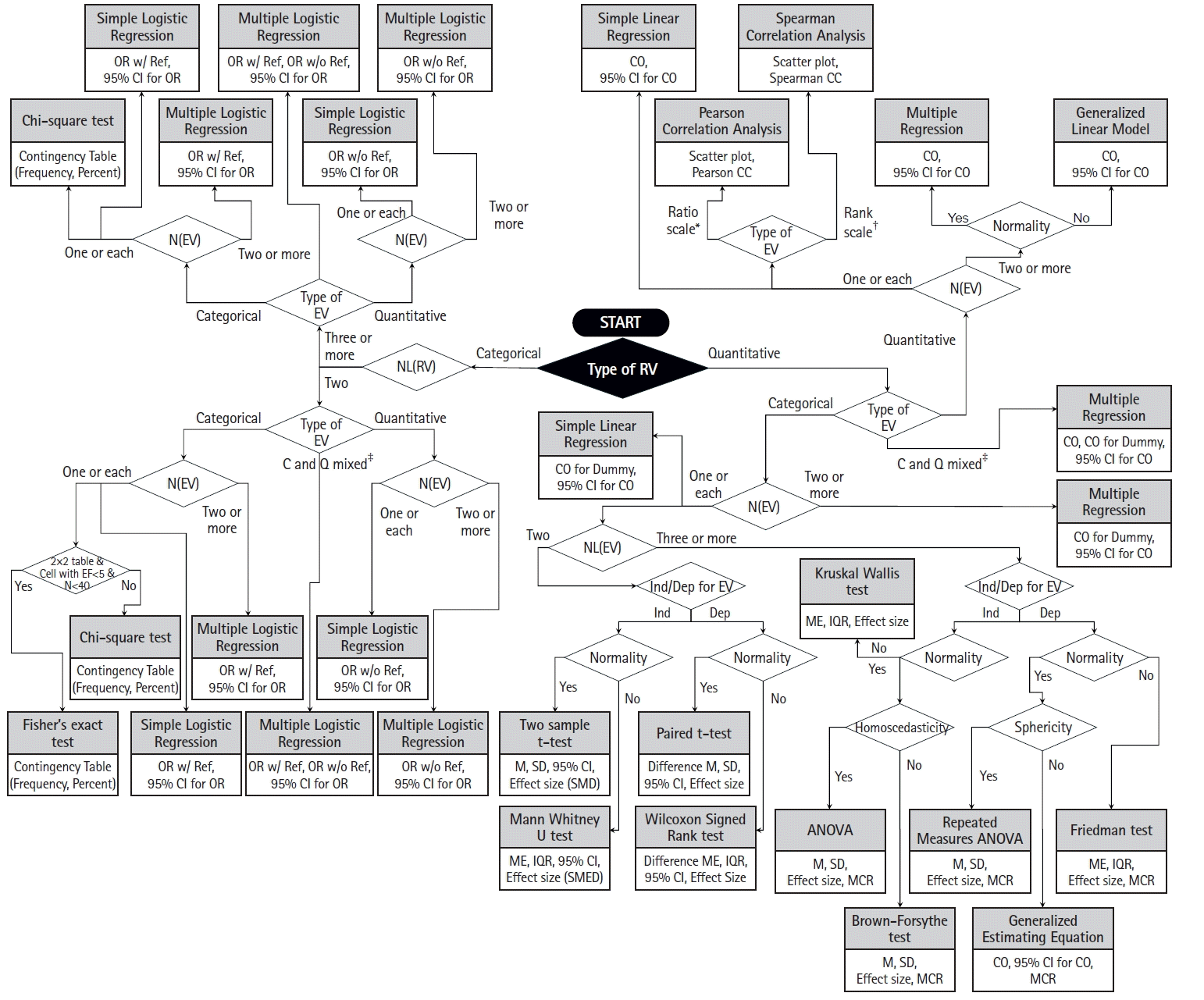
Fig. 2.
Application of the flowchart for selecting the statistical analysis method to the study by Lee et al. (Lee JH, Kim HJ, Kim JK, Cheon S, Shin YH. Does intravenous patient-controlled analgesia or continuous block prevent rebound pain following infraclavicular brachial plexus block after distal radius fracture fixation? A prospective randomized controlled trial. Korean J Anesthesiol 2023; 76: 559-66), in which the Kruskal-Wallis test was used. ANOVA: analysis of variance, C: categorical, CO: coefficient, Dep: dependent, EV: explanatory variable, Ind: independent, IQR: interquartile range, M: mean, MCR: multiple comparison result, ME: median, N(EV): number of explanatory variables, NL(EV): number of levels for the explanatory variable, Q: quantitative, RV: response variable, SD: standard deviation, SMD: standardized mean difference, SMED: standardized median difference. *C and Q mixed: explanatory variables have at least one categorical and one quantitative variable.
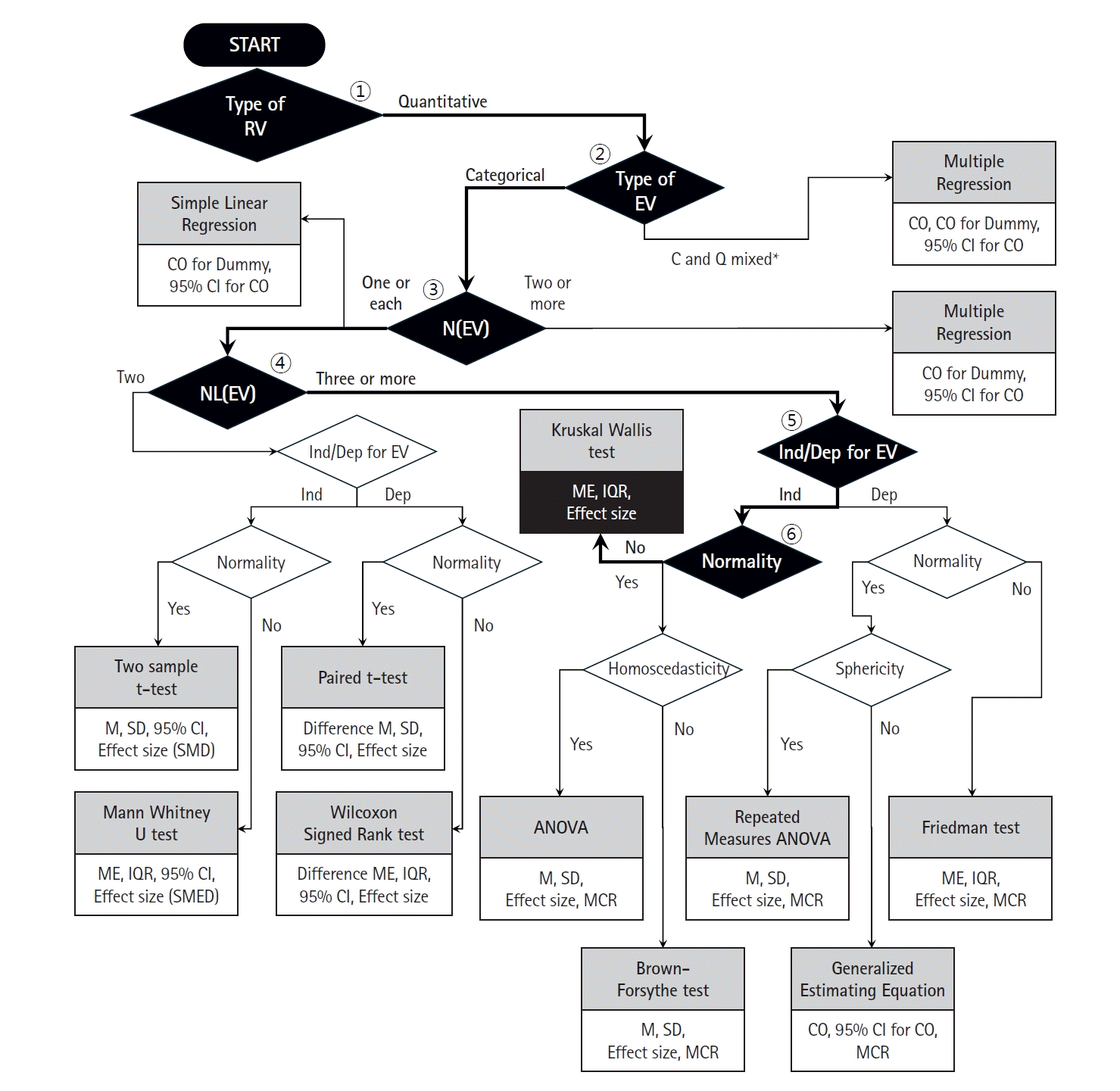
Fig. 3.
Application of the flowchart for selecting the statistical analysis method to the study by Lee et al. (Lee JH, Kim HJ, Kim JK, Cheon S, Shin YH. Does intravenous patient-controlled analgesia or continuous block prevent rebound pain following infraclavicular brachial plexus block after distal radius fracture fixation? A prospective randomized controlled trial. Korean J Anesthesiol 2023; 76: 559-66), in which the chi-square test was used. C: categorical, EF: expected frequency, EV: explanatory variable, N: number of subjects, N(EV): number of explanatory variables, NL(RV): number of levels for the response variable, OR: odds ratio, Q: quantitative, Ref: reference, RV: response variable, w/: with, w/o: without. *C and Q mixed: explanatory variables have at least one categorical and one quantitative variable.
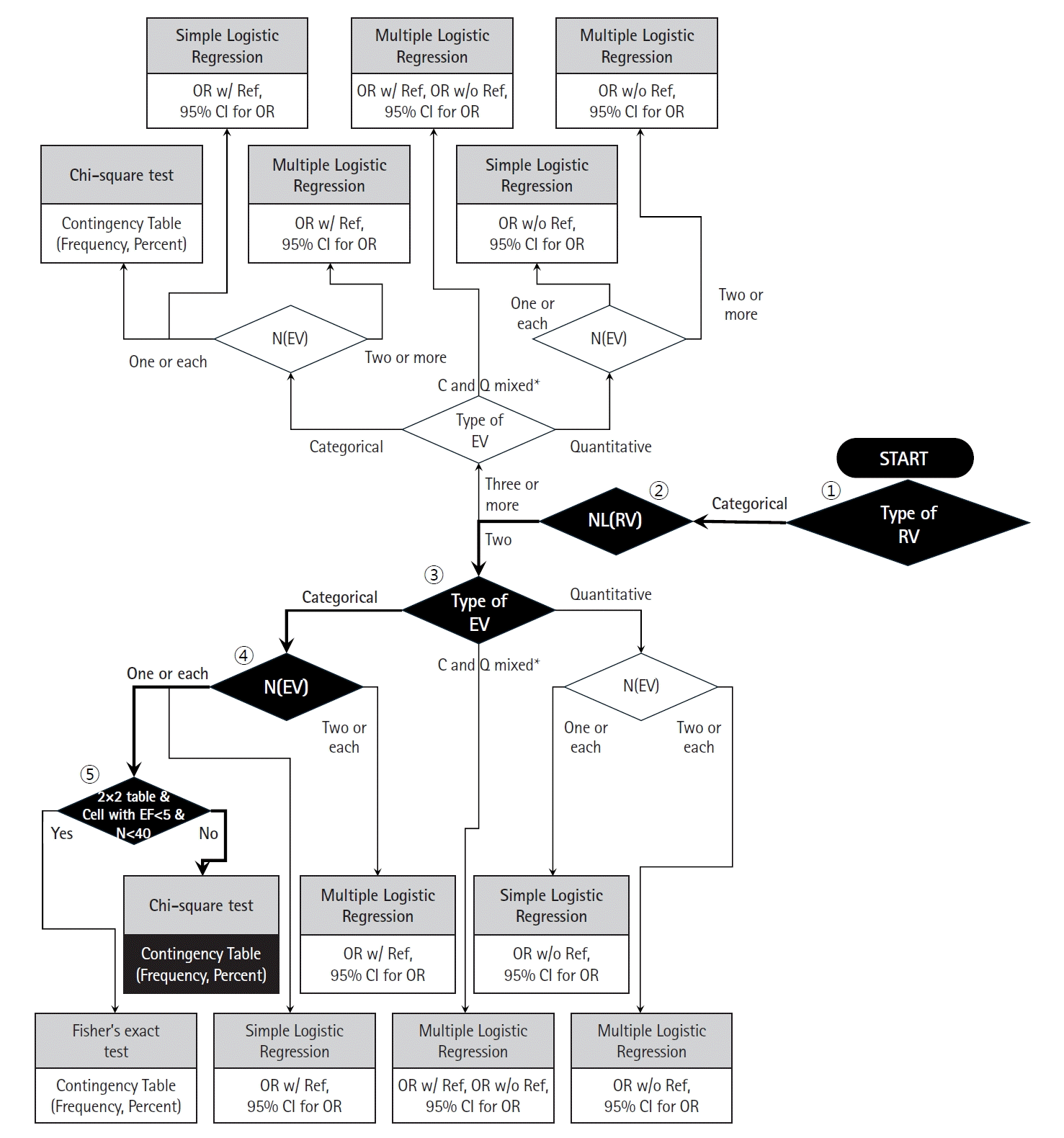
Fig. 4.
Application of the flowchart for selecting the statistical analysis method to the study by Genç Perdecioğlu et al. (Genç Perdecioğlu GR, Panpallı Ateş M, Yürük D, Akkaya ÖT. Neuromodulation of the median nerve in carpal tunnel syndrome, a single-blind, randomized controlled study. Korean J Pain 2024; 37: 34-40), in which the two-sample t-test was used. ANOVA: analysis of variance, C: categorical, CO: coefficient, Dep: dependent, EV: explanatory variable, Ind: independent, IQR: interquartile range, M: mean, MCR: multiple comparison result, ME: median, N(EV): number of explanatory variables, NL(EV): number of levels for the explanatory variable, Q: quantitative, RV: response variable, SD: standard deviation, SMD: standardized mean difference, SMED: standardized median difference. *C and Q mixed: explanatory variables have at least one categorical and one quantitative variable.
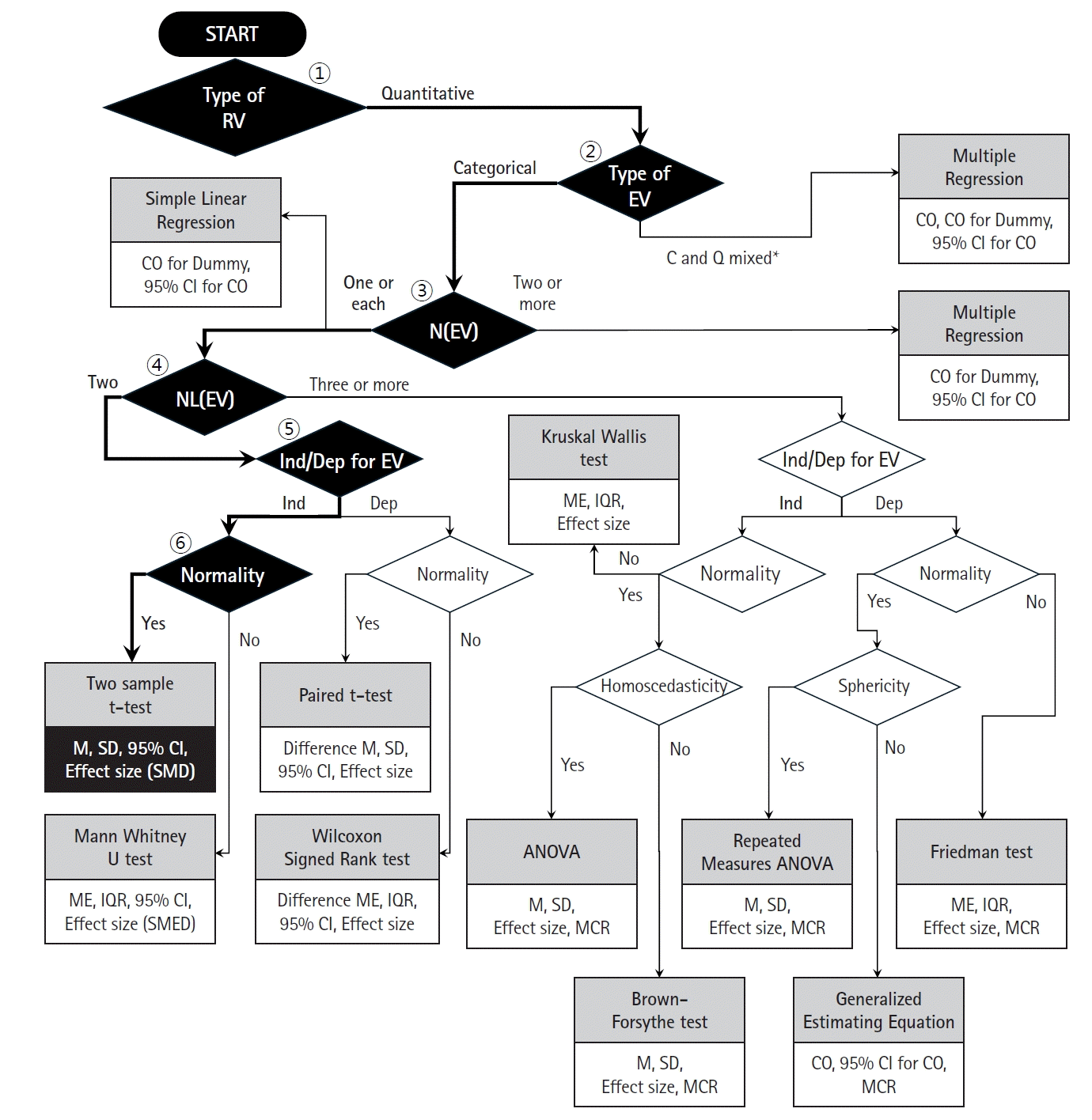
Fig. 5.
Application of the flowchart for selecting the statistical analysis method to the study by Genç Perdecioğlu et al. (Genç Perdecioğlu GR, Panpallı Ateş M, Yürük D, Akkaya ÖT. Neuromodulation of the median nerve in carpal tunnel syndrome, a single-blind, randomized controlled study. Korean J Pain 2024; 37: 34-40), in which the repeated-measures ANOVA was used. ANOVA: analysis of variance, C: categorical, CO: coefficient, Dep: dependent, EV: explanatory variable, Ind: independent, IQR: interquartile range, M: mean, MCR: multiple comparison result, ME: median, N(EV): number of explanatory variables, NL(EV): number of levels for the explanatory variable, Q: quantitative, RV: response variable, SD: standard deviation, SMD: standardized mean difference, SMED: standardized median difference. *C and Q mixed: explanatory variables have at least one categorical and one quantitative variable.
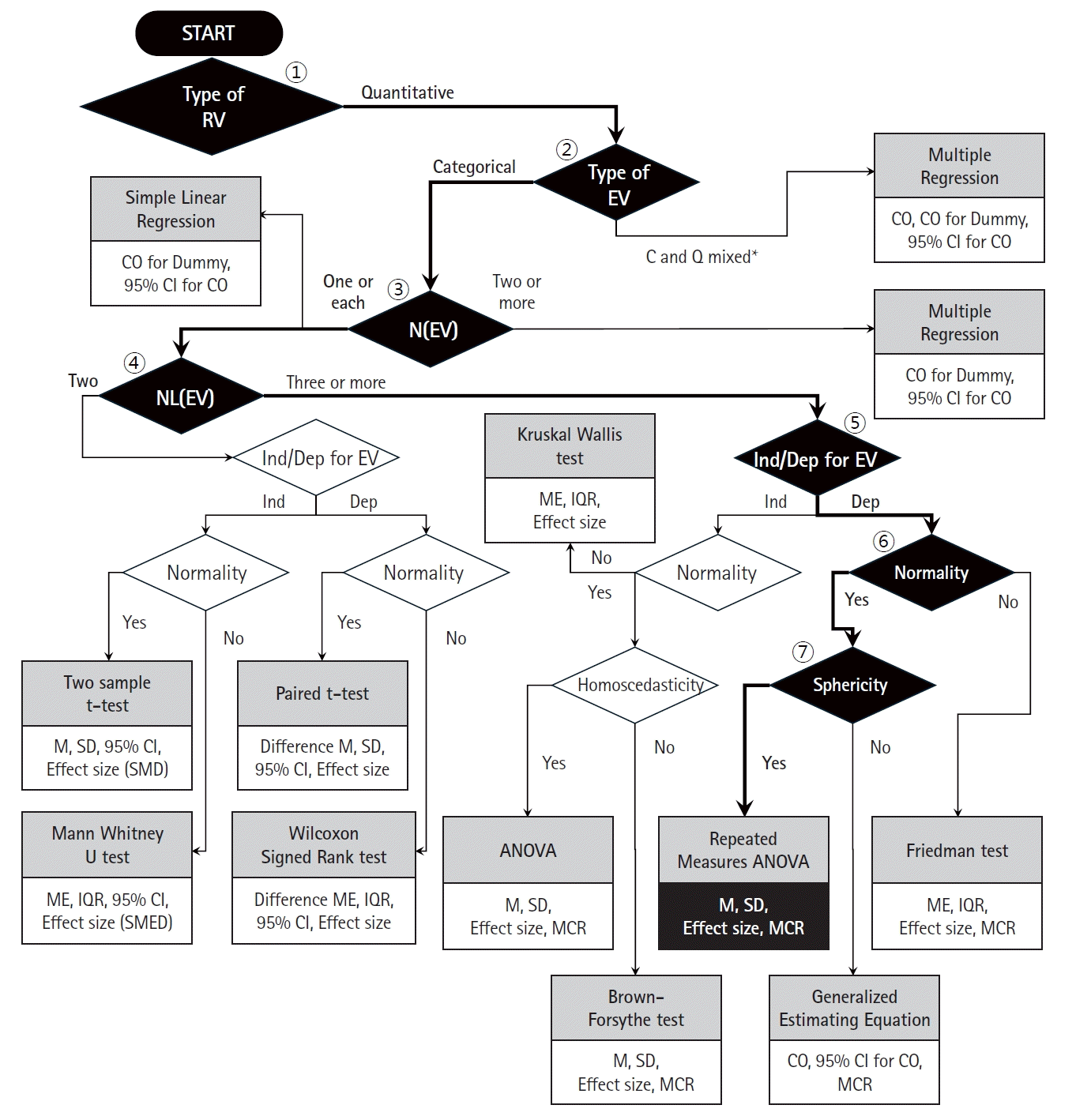
Table 1.
Types of Variables, Null Hypotheses, and Alternative Hypotheses for Various Statistical Analysis Methods
Table 2.
Classification of Logistic Regression Analyses according to the Number of Explanatory Variables and Levels for the Response Variable




 PDF
PDF Citation
Citation Print
Print



 XML Download
XML Download