Abstract
Objectives
This study aimed to optimize early coronary heart disease (CHD) prediction using a genetic algorithm (GA)-based convolutional neural network (CNN) feature engineering approach. We sought to overcome the limitations of traditional hyperparameter optimization techniques by leveraging a GA for superior predictive performance in CHD detection.
Methods
Utilizing a GA for hyperparameter optimization, we navigated a complex combinatorial space to identify optimal configurations for a CNN model. We also employed information gain for feature selection optimization, transforming the CHD datasets into an image-like input for the CNN architecture. The efficacy of this method was benchmarked against traditional optimization strategies.
Results
The advanced GA-based CNN model outperformed traditional methods, achieving a substantial increase in accuracy. The optimized model delivered a promising accuracy range, with a peak of 85% in hyperparameter optimization and 100% accuracy when integrated with machine learning algorithms, namely naïve Bayes, support vector machine, decision tree, logistic regression, and random forest, for both binary and multiclass CHD prediction tasks.
Conclusions
The integration of a GA into CNN feature engineering is a powerful technique for improving the accuracy of CHD predictions. This approach results in a high degree of predictive reliability and can significantly contribute to the field of AI-driven healthcare, with the possibility of clinical deployment for early CHD detection. Future work will focus on expanding the approach to encompass a wider set of CHD data and potential integration with wearable technology for continuous health monitoring.
Coronary heart disease (CHD), identified by the World Health Organization as a leading cause of death, develops from arterial blockages that impair heart function. Each year, CHD claims approximately 17.9 million lives, underscoring the importance of early detection and personalized management to reduce patient risk [1]. In healthcare, the use of artificial intelligence (AI), machine learning, and deep learning is on the rise, with deep learning particularly showing potential in improving the prognosis of CHD and customizing patient care [2]. While these technologies play a crucial role in enhancing prediction accuracy [3], predicting CHD remains a challenging task [4].
Machine learning has shown promising results in predicting coronary heart disease by developing models that utilize established risk indicators such as age, sex, blood pressure, cholesterol levels, smoking habits, and family medical history. Key algorithms, including naive Bayes, XGBoost, k-nearest neighbor, multilayer perceptron, and support vector machine (SVM) [5], have been used in these predictions. Feature selection, particularly through information gain (IG), plays a crucial role in enhancing the accuracy, simplicity, and efficiency of these models. This leads to more accurate, interpretable models that are well-suited for practical application in various real-world settings [6]. IG is instrumental in identifying the most critical features for predicting CHD [7], thus optimizing the prediction process.
Hyperparameter optimization plays a crucial role in machine learning, aiming to improve model accuracy and prevent overfitting by achieving a balance in variation. This process involves setting specific model configurations that are not derived from data but are selected to boost network performance. Common techniques such as grid search [8], randomized search [9], and Bayesian optimization [10] are frequently utilized because the success of a model is significantly influenced by the values of its hyperparameters [11]. The extensive range of hyperparameter combinations presents a considerable challenge [12] and is approached as a multi-objective problem to optimize performance indices [13]. Meta-heuristic methods, including the ant colony system [14] and genetic algorithms (GAs) [15], address this issue by exploring optimal configurations. Our study utilized a GA, as GAs have proven to be effective in optimizing hyperparameters.
Employing feature engineering with a convolutional neural network (CNN) involves the automatic extraction and representation of relevant features from raw data by the network itself. The CNN is specifically designed to learn and extract features hierarchically through its convolutional layers, which automatically identify discriminative features from raw data, thus reducing the reliance on manual feature engineering [16]. This approach eliminates the need for human-designed features and enables the network to autonomously identify essential patterns in the data. CNNs offer high accuracy and flexibility, depending on sufficient data for their design and training, and facilitate enhanced classification across various domains [17]. Determining the hyperparameters is crucial for effective performance. GA-based CNNs have demonstrated satisfactory results in applications such as crop pest image classification [18], croup cough classification [19], and pattern recognition [20]. They also have the potential to improve the outcomes of CHD prediction.
Utilizing a GA-based CNN for hyperparameter optimization offers several advantages over traditional methods. GAs are particularly effective at balancing exploration and exploitation, which helps them avoid local minima and identify optimal hyperparameters. This capability renders them computationally superior to exhaustive methods such as grid search. Additionally, GAs are highly adaptable, capable of managing the complex, high-dimensional search spaces typical of deep learning models. Their scalability facilitates the efficient optimization of large models, and the mechanisms of crossover and mutation contribute to preventing overfitting. Moreover, the parallelizability of GAs enhances their efficiency by allowing the simultaneous evaluation of multiple solutions. Overall, this approach provides a robust and flexible solution for optimizing CHD prediction models.
Public datasets for CHD prediction, such as the Cleveland dataset from the UCI Machine-Learning Repository, are structured in tabular form. However, CNNs, which are primarily designed for image data, encounter challenges when processing tabular data. Converting tabular data into images [21] preserves spatial information, enabling CNNs to effectively capture spatial dependencies and patterns [22]. This method improves the model’s ability to detect intricate patterns and relationships that might not be fully discernible when using tabular data directly with a CNN.
This study introduced a GA-based CNN feature engineering method aimed at optimizing the accuracy of early CHD detection. The main contributions of this research include: (1) utilizing IG for the selection of critical features; (2) improving the prediction performance of early CHD detection through the application of GA for hyperparameter tuning in CNN; and (3) converting tabular data into image format to more effectively capture spatial correlations and improve CHD prediction accuracy.
In this study, the Cleveland dataset from the UCI Machine Learning Repository was employed. This database includes 76 features, with a particular focus on the target feature that indicates the presence of heart disease. Typically, research has concentrated on a subset of 14 attributes from records of 303 patients. The dataset is primarily used for binary classification to distinguish between cases with heart disease (499 instances) and those without (526 instances). Additionally, a multiclass risk stratification approach was employed to categorize instances into five levels: class 0 (no heart disease), class 1 (low risk, 55 instances), class 2 (moderate risk, 36 instances), class 3 (high risk, 35 instances), and class 4 (very high risk, 13 instances).
This paper introduces a CNN that is enhanced by a GA and specifically designed for the early detection of CHD, as illustrated in Figure 1. The approach was structured as follows: initially, a CHD dataset was acquired and preprocessed to address missing values. Subsequently, an IG technique was employed to identify the most predictive features, which were then converted into an image-like format suitable for CNN analysis. The CNN was further refined using a GA that optimized its hyperparameters, improving its feature extraction capabilities. The optimized features were then utilized to train various machine learning classifiers, including naive Bayes, SVM, decision tree, and logistic regression. A rigorous evaluation employing metrics such as accuracy, precision, recall, and F-measure showed that this comprehensive approach, which integrates data preparation, feature engineering, and machine learning, markedly improved the accuracy of CHD prediction.
For feature selection, as illustrated in Figure 2A, IG was utilized to identify the most predictive features. This involved several steps: calculating entropy, determining the conditional entropy for each feature, computing IG, and ranking the features. This phase focuses on selecting the most informative features, ensuring that the model highlights the key predictors of CHD. The subsequent challenge involves adapting the tabular CHD dataset for CNN application by transforming it into a three-dimensional, image-like structure. Figure 2B outlines this transformation process, which includes defining the dataset dimensions, specifying the number of channels based on grouped categories from the selected features, and configuring them into a 3 × 4 × 1 input shape for CNN analysis.
As illustrated in Figure 2C, our GA-based CNN starts with an input layer designed to accommodate a 3 × 4 × 1 representation of the dataset’s features. Following this, the convolutional layer carries out several convolution operations, each succeeded by batch normalization to improve training speed and stability.
A GA optimizes the hyperparameters of the CNN. It generates potential solutions (sets of hyperparameters), applies crossover and mutation, and evaluates their fitness, such as accuracy. The best solutions are selected for subsequent generations, ultimately converging on an optimal set. The output of this optimized CNN serves as a refined feature set, which enhances the accuracy of traditional machine learning models in predicting CHD. The performance is rigorously evaluated using metrics such as accuracy, precision, recall, F1-score, specificity, G-mean, and p-value.
An evaluation was conducted to assess the performance of CHD prediction using several metrics beyond accuracy, providing a comprehensive overview of the model’s capabilities. This included an analysis of recall, precision, F1-score, specificity, and G-mean. Additionally, we report the p-value for each metric to demonstrate their statistical significance. This expanded evaluation provides a more nuanced understanding of the model’s strengths and limitations across different performance dimensions.
For this study, the CHD dataset was thoroughly examined for missing values to ensure data integrity and completeness. Upon inspection, it was observed that the CHD dataset contained no missing values in either the binary or multiclass datasets. The absence of missing values simplifies the preprocessing stage, allowing us to proceed directly to feature selection and modeling without the need for imputation strategies.
Using IG for feature selection, 12 features were identified as significant for both the binary and multiclass CHD datasets. In the binary dataset, the significant features along with their IG values are as follows: cholesterol (“chol,” 0.212439), maximum heart rate (“thalach,” 0.164900), chest pain (“cp,” 0.150377), ST depression (“oldpeak,” 0.148694), thalassemia (“thal,” 0.138485), visible vessels (“ca,” 0.111282), exercise angina (“exang,” 0.094309), age (0.085682), heart rate slope (“slope,” 0.076467), resting blood pressure (“trestbps,” 0.060951), sex (“sex,” 0.046134), and ECG results (“restecg,” 0.009632). Fasting blood sugar (“fbs”) with a value of 0.000000 was not considered informative. The correlations among these features are depicted in Figure 3A.
For the multiclass dataset, the notable features were chest pain (“cp,” 0.141675), thalassemia (“thal,” 0.127007), exercise angina (“exang,” 0.111727), maximum heart rate (“thalach,” 0.090939), ST depression (“oldpeak,” 0.090754), visible vessels (“ca,” 0.076833), heart rate slope (“slope,” 0.076124), and age (0.027281). Interestingly, gender (“sex”), resting blood pressure (“trestbps”), cholesterol (“chol”), and ECG results (“restecg”) each had an IG of zero and were excluded from the model. The heatmap displayed in Figure 3B illustrates the correlation among the features in the multiclass dataset. In contrast to the binary set, this dataset did not include sex as a factor.
The transformation of the CHD dataset into an image representation resulted in an input shape for the CNN comprising 303 samples. Each sample includes three channels, with each channel containing four features, leading to a total format of 303 × 3 × 4 × 1. Consider, for example, the features of a single CHD sample: age, cholesterol level, blood pressure, and heart rate. These features are normalized and mapped onto three distinct color channels (e.g., red, green, and blue). Each feature was then positioned within a 4 × 1 grid for each channel. Figure 4 illustrates this concept, where a specific combination of feature values is visually represented. The intensity of each color within a square corresponds to the normalized value of a feature, providing a comprehensive visual summary of the dataset.
A GA with a population of 10 across 10 generations was used to perform optimization, thereby improving the CNN’s feature-processing layer. Initially, the GA was applied to the binary CHD dataset, and subsequently, the determined optimal hyperparameters were also used for the multiclass CHD data.
Figure 5A depicts the validation accuracy achieved at each stage of the GA evolution, while Figure 5B displays the minimum, maximum, and average validation accuracies across 10 GA generations. An analysis of these figures reveals that the highest hyperparameter optimization accuracy reached 85.1021%. This peak performance was achieved using a combination of various filter sizes, fully connected layer sizes, activation functions (“selu” and “relu”), and the “adagrad” optimizer over a span of 140 epochs. In contrast, the lowest accuracy recorded was 57.2591%, achieved with a slightly altered set of parameters for the filters and layers, but using the same “adagrad” optimizer, this time over 139 epochs. These specific hyperparameter configurations demonstrate their influence on the model’s validation accuracy.
Figure 6 illustrates the performance of the hyperparameter optimization using the GA-based CNN throughout the training and testing phases. Several machine learning algorithms, including naïve Bayes, SVM, decision tree, logistic regression, and random forest, have been utilized for CHD prediction due to their proven effectiveness in previous studies.
Tables 1 and 2 present the results of applying different machine learning algorithms to the binary and multiclass CHD datasets, respectively. These results specifically demonstrate the performance achieved using the highest hyperparameter optimization accuracy of 85.1021%, as determined by our GA-based CNN feature engineering approach. It is important to note that our exploration of hyperparameter optimization produced a spectrum of accuracies, with the lowest recorded accuracy being 57.2591%.
This study shows that integrating a GA with a CNN substantially enhances the prediction of CHD. Our approach surpassed traditional feature engineering, achieving 100% accuracy and highlighting the effectiveness of genetic algorithms in automating feature selection within complex datasets.
Comparisons with existing methodologies revealed that our GA-based CNN model exhibited superior performance, as illustrated in Table 3 [9,23–26], compared to previously reported methods. In particular, our proposed method achieved an accuracy of 100%. This is in contrast to the previous high accuracies, such as 97.52% reported by Valarmathi and Sheela [9] using random forest and XGBoost with grid and randomized search for hyperparameter optimization, and 99.51% accuracy reported by Najafi et al. [27], which involved particle swarm optimization.
While our focus on IG for feature selection demonstrated that exploring various methods, such as Lasso-CNN with different optimization techniques (e.g., particle swarm optimization), can achieve accuracies exceeding 97% [9], this highlights the impact of methodological choices and dataset characteristics on performance. This aligns with our emphasis on multi-criteria evaluation. Additionally, our work introduces a novel approach to CHD prediction compared to that used by Najafi et al. [27], utilizing a GA-based CNN for feature engineering and representing tabular data in an image-like format, which improves the analysis capabilities of the CNN.
The significance of our GA-based CNN model lies in its substantial potential to enhance public health through improved CHD detection accuracy. This improvement could facilitate better prevention strategies and more personalized medical treatments. By employing genetic algorithms for feature engineering, this approach not only boosts prediction precision but also supports the development of AI tools in healthcare. The success of this model underscores the critical role of interdisciplinary collaboration in incorporating such innovations into clinical practice, ultimately enhancing patient care and healthcare efficiency.
While promising, the findings of our study must be viewed within the context of certain limitations that could affect their broader applicability. One significant limitation is the sample size and diversity of the dataset. If our research depended on a dataset that was either too small or not representative, it could limit the model’s ability to extrapolate to different demographics, including variations in ethnicity, age groups, or regions characterized by distinct CHD patterns and risk profiles.
The exclusive reliance on historical data presents another limitation, as it may introduce biases that could skew the model’s predictive capacity. To enhance future studies, incorporating a more inclusive dataset that includes prospective data and diverse ethnic backgrounds would help ensure the robustness of the results across various populations. Additionally, the predictive performance may differ between research and clinical settings, as real-world applications necessitate thorough model validation and adjustments to accommodate the complexities of clinical data variability and operational integration.
Finally, despite the strong performance in feature selection and hyperparameter refinement, there is a risk of overfitting when dealing with complex datasets. It is imperative to confirm the model’s ability to generalize to new and unseen data, which is critical for its practical applicability in healthcare.
Future research should prioritize multi-institutional validation of GA-based CNN to confirm its applicability and effectiveness across diverse patient groups. Prospective clinical trials are crucial for evaluating its integration and performance in real-world settings. Further investigative efforts could also explore synergies with other machine learning methods to enhance and potentially increase the prediction accuracy. Efficient integration of the model within clinical workflows and electronic health record systems is essential for its practical adoption. Concurrently, the ethical use of AI and cost-effectiveness analyses will play a significant role in determining the model’s sustainability and its alignment with healthcare priorities, thereby advancing the role of AI in personalized patient care.
In conclusion, this study underscores the effectiveness of GA-based feature engineering in optimizing CNNs for CHD prediction. Our approach marks a substantial advancement in the use of machine learning techniques within the field of cardiovascular medicine.
Acknowledgments
We thank the Office of Research and Community Service (LPPM) Universitas Dian Nuswantoro (UDINUS) for all the support that made this study possible, under contract number 109/A.38-04/UDN-09/XI/2023.
References
1. Muhammad Y, Tahir M, Hayat M, Chong KT. Early and accurate detection and diagnosis of heart disease using intelligent computational model. Sci Rep. 2020; 10(1):19747. https://doi.org/10.1038/s41598-020-76635-9.

2. Zhang P, Xu F. Effect of AI deep learning techniques on possible complications and clinical nursing quality of patients with coronary heart disease. Food Sci Technol. 2022; 42:e42020. https://doi.org/10.1590/fst.42020.

3. Elwahsh H, El-Shafeiy E, Alanazi S, Tawfeek MA. A new smart healthcare framework for real-time heart disease detection based on deep and machine learning. PeerJ Comput Sci. 2021; 7:e646. https://doi.org/10.7717/peerjcs.646.

4. Al-Alshaikh HA, PP , Poonia RC, Saudagar AKJ, Yadav M, AlSagri HS, et al. Comprehensive evaluation and performance analysis of machine learning in heart disease prediction. Sci Rep. 2024; 14(1):7819. https://doi.org/10.1038/s41598-024-58489-7.

5. Kanagarathinam K, Sankaran D, Manikandan R. Machine learning-based risk prediction model for cardiovascular disease using a hybrid dataset. Data Knowl Eng. 2022; 140:102042. https://doi.org/10.1016/j.datak.2022.102042.
6. Theng D, Bhoyar KK. Feature selection techniques for machine learning: a survey of more than two decades of research. Knowl Inf Syst. 2024; 66:1575–637. https://doi.org/10.1007/s10115-023-02010-5.

7. Kurniabudi , Stiawan D, Darmawijoyo , Bin Idris MY, Bamhdi AM, Budiarto R. CICIDS-2017 dataset feature analysis with information gain for anomaly detection. IEEE Access. 2020; 8:132911–21. https://doi.org/10.1109/ACCESS.2020.3009843.

8. Kaur S, Aggarwal H, Rani R. Hyper-parameter optimization of deep learning model for prediction of Parkinson’s disease. Mach Vis Appl. 2020; 31:32. https://doi.org/10.1007/s00138-020-01078-1.

9. Valarmathi R, Sheela T. Heart disease prediction using hyper parameter optimization (HPO) tuning. Biomed Signal Process Control. 2021; 70:103033. https://doi.org/10.1016/j.bspc.2021.103033.

10. Montesinos-Lopez OA, Carter AH, Bernal-Sandoval DA, Cano-Paez B, Montesinos-Lopez A, Crossa J. A comparison between three tuning strategies for gaussian kernels in the context of univariate genomic prediction. Genes (Basel). 2022; 13(12):2282. https://doi.org/10.3390/genes13122282.

11. Ghawi R, Pfeffer J. Efficient hyperparameter tuning with grid search for text categorization using kNN approach with BM25 similarity. Open Comput Sci. 2019; 9(1):160–80. https://doi.org/10.1515/comp-2019-0011.

12. Kumar S, Ratnoo S. Multi-objective hyperparameter tuning of classifiers for disease diagnosis. Indian J Comput Sci Eng. 2021; 12(5):1334–52. https://doi.org/10.21817/indjcse/2021/v12i5/211205081.

13. Rusch T, Mair P, Hornik K. Structure-based hyperparameter selection with Bayesian optimization in multidimensional scaling. Stat Comput. 2023; 33(1):28. https://doi.org/10.1007/s11222-022-10197-w.

14. Lankford S, Grimes D. Neural architecture search using particle swarm and ant colony optimization [Internet]. Ithaca (NY): arXiv.org;2024. [cited at 2024 Jul 30]. Available from: http://arxiv.org/pdf/2403.03781.
15. Tayebi M, El Kafhali S. Hyperparameter optimization using genetic algorithms to detect frauds transactions. In : Proceedings of the International Conference on Artificial Intelligence and Computer Vision (AICV2021); Cham, Switzerland: Springer;2021; p. 288–97. https://doi.org/10.1007/978-3-030-76346-6_27.

16. Alzubaidi L, Zhang J, Humaidi AJ, Al-Dujaili A, Duan Y, Al-Shamma O, et al. Review of deep learning: concepts, CNN architectures, challenges, applications, future directions. J Big Data. 2021; 8(1):53. https://doi.org/10.1186/s40537-021-00444-8.

17. Kong Y, Wang X, Cheng Y, Chen CL. Multi-stage convolutional broad learning with block diagonal constraint for hyperspectral image classification. Remote Sens. 2021; 13(17):3412. https://doi.org/10.3390/rs13173412.

18. Ayan E. Genetic algorithm-based hyperparameter optimization for convolutional neural networks in the classification of crop pests. Arab J Sci Eng. 2024; 49:3079–93. https://doi.org/10.1007/s13369-023-07916-4.

19. Vetrimani E, Arulselvi M, Ramesh G. Building convolutional neural network parameters using genetic algorithm for the croup cough classification problem. Measur Sens. 2023; 27:100717. https://doi.org/10.1016/j.measen.2023.100717.

20. Montecino DA, Perez CA, Bowyer KW. Two-level genetic algorithm for evolving convolutional neural networks for pattern recognition. IEEE Access. 2021; 9:126856–72. https://doi.org/10.1109/ACCESS.2021.3111175.

21. Salam A, Zeniarja J. Classification of deep learning convolutional neural network feature extraction for student graduation prediction. Indones J Electr Eng Comput Sci. 2023; 32(1):335. https://doi.org/10.11591/ijeecs.v32.i1.pp335-341.

22. Zhu Y, Brettin T, Xia F, Partin A, Shukla M, Yoo H, et al. Converting tabular data into images for deep learning with convolutional neural networks. Sci Rep. 2021; 11(1):11325. https://doi.org/10.1038/s41598-021-90923-y.

23. Hassan D, Hussein HI, Hassan MM. Heart disease prediction based on pre-trained deep neural networks combined with principal component analysis. Biomed Signal Proc Contr. 2023; 79(Part 1):104019. https://doi.org/10.1016/j.bspc.2022.104019.

24. El Sherbiny MM, Abdelhalim E, Mostafa HE, El-Seddik MM. Classification of chronic kidney disease based on machine learning techniques. Indones J Electr Eng Comput Sci. 2023; 32(2):945. https://doi.org/10.11591/ijeecs.v32.i2.pp945-955.
25. Narisetty N, Kalidindi A, Bujaranpally MV, Arigela N, Ch VV. Ameliorating heart diseases prediction using machine learning technique for optimal solution. Int J Online Biomed Eng (iJOE). 2023; 19(16):156–65. https://doi.org/10.3991/ijoe.v19i16.42071.

26. El-Ibrahimi A, Terrada O, El Gannour O, Cherradi B, El-Abbassi A, Bouattane O. Optimizing machine learning algorithms for heart disease classification and prediction. Int J Online Biomed Eng (iJOE). 2023; 19(15):61–76. https://doi.org/10.3991/ijoe.v19i15.42653.

27. Najafi A, Nemati A, Ashrafzadeh M, Zolfani SH. Multiple-criteria decision making, feature selection, and deep learning: a golden triangle for heart disease identification. Eng Appl Artif Intell. 2023; 125:106662. https://doi.org/10.1016/j.engappai.2023.106662.

Figure 1
Research framework of the proposed genetic algorithm (GA)-based convolutional neural network (CNN) for feature engineering in coronary heart disease (CHD) prediction. NB: naive Bayes, SVM: support vector machine, DT: decision tree, LR: logistic regression.
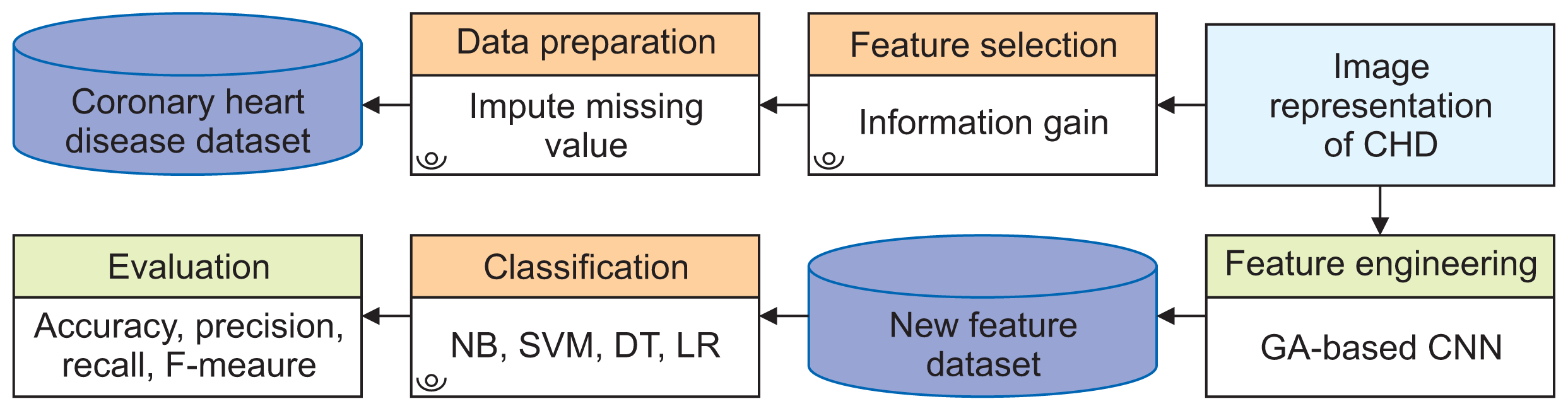
Figure 2
(A) Application of information gain for feature selection, (B) process of converting tabular data to an image-like format, and (C) implementation of genetic algorithm (GA)-based convolutional neural network (CNN) feature engineering. CHD: coronary heart disease.
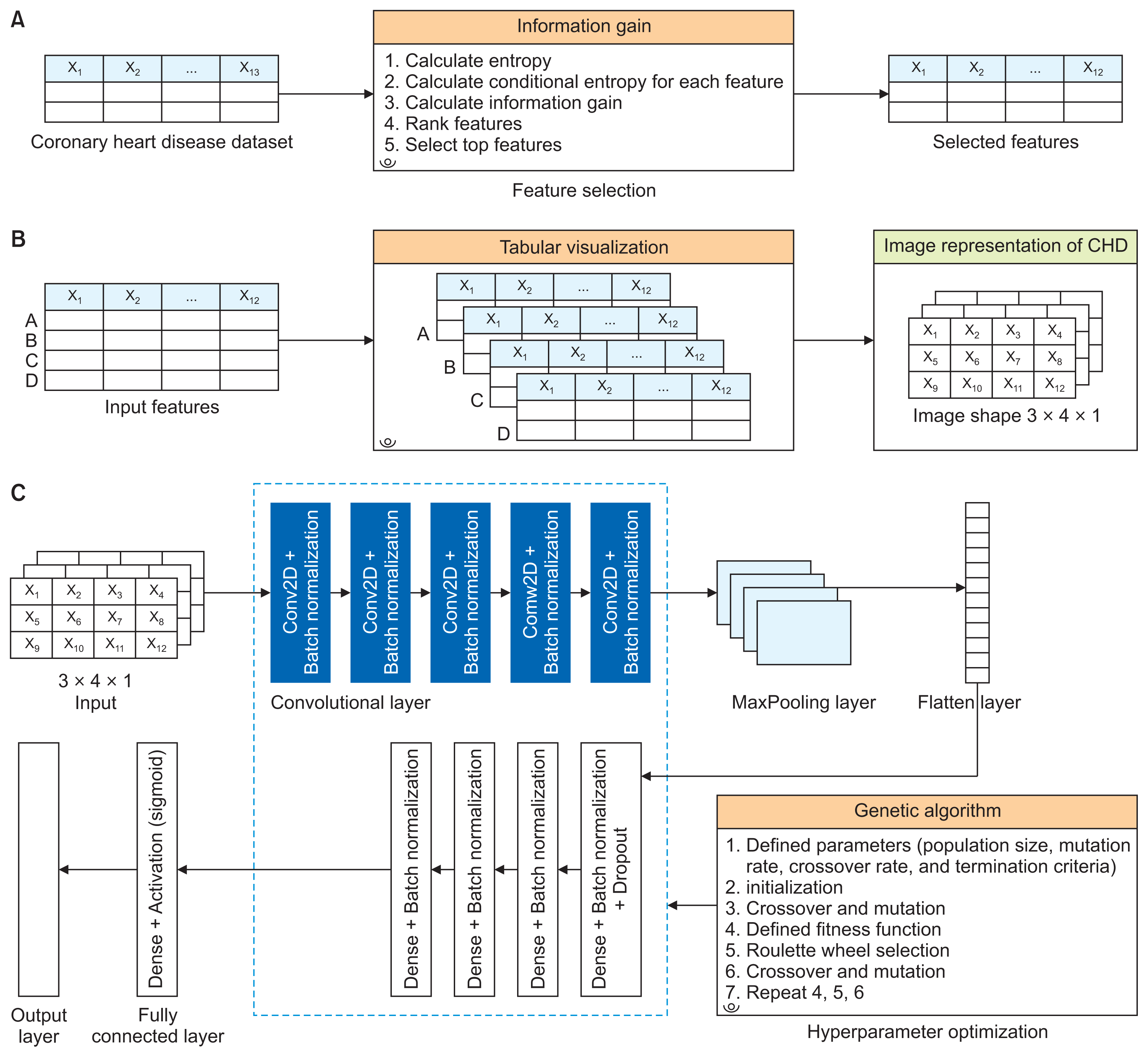
Figure 3
Heatmap illustrating feature correlations for (A) the binary coronary heart disease (CHD) dataset and (B) the multiclass CHD dataset.
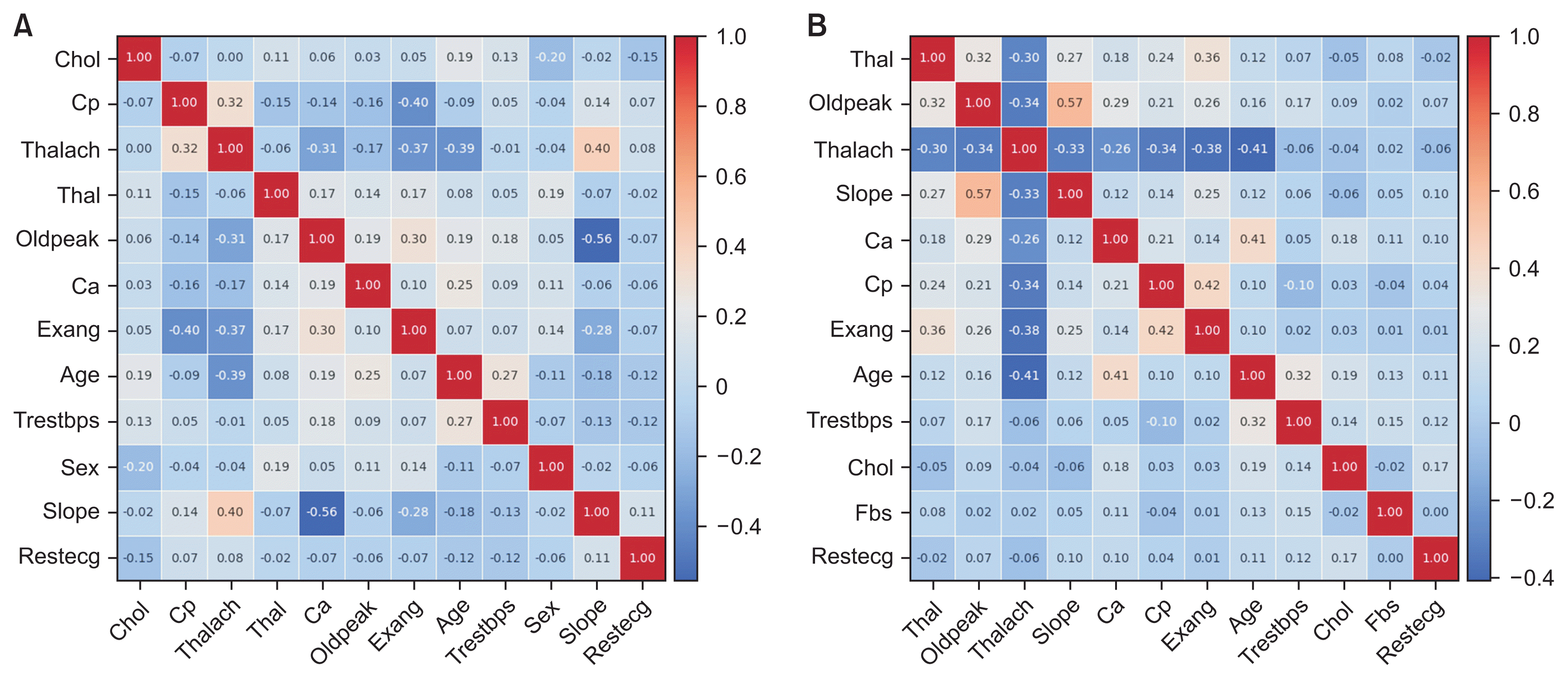
Figure 5
(A) Trends in validation accuracy throughout each genetic algorithm evolution and (B) summary of minimum, maximum, and average performance metrics across 10 generations of the genetic algorithm.
Figure 6
Performance outcomes from hyperparameter optimization using genetic algorithm for the convolutional neural network model applied to coronary heart disease prediction: (A) accuracy and (B) loss.
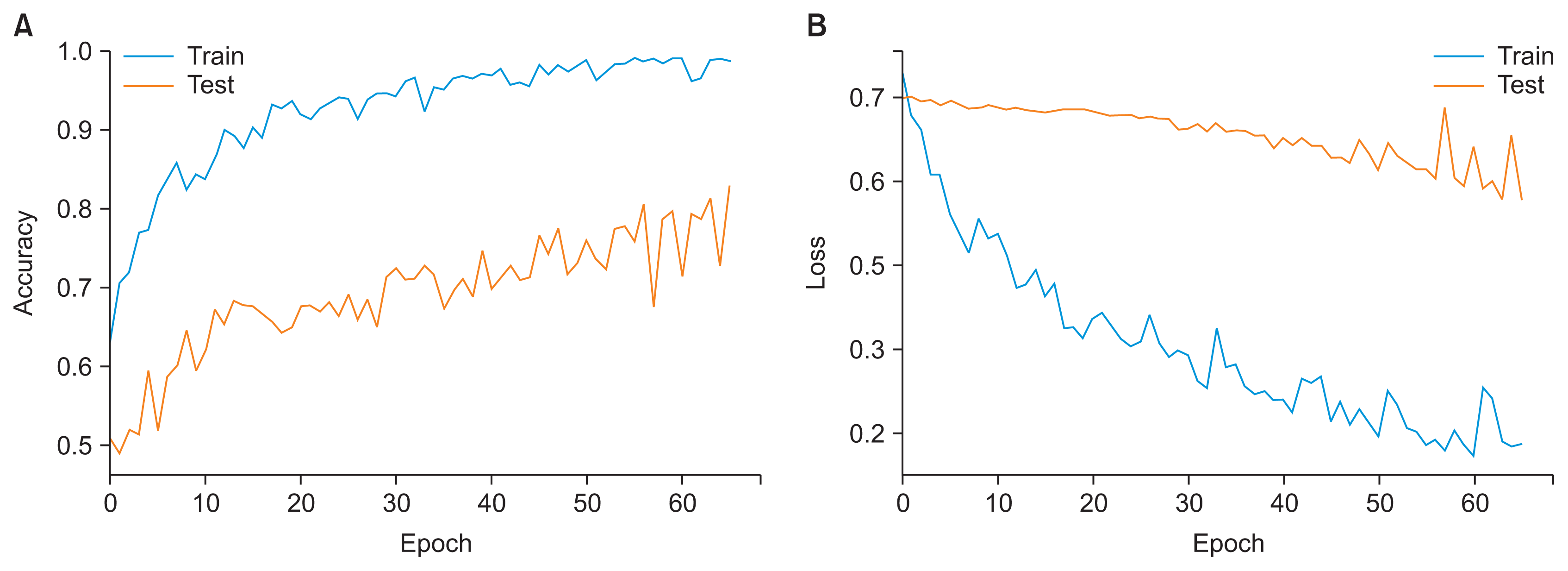
Table 1
Results for the binary dataset using the highest hyperparameter optimization accuracy of 85.1021% (unit: %)
Table 2
Results for the multiclass dataset using the highest hyperparameter optimization accuracy of 85.1021% (unit: %)
Table 3
Comparative performance of the proposed method compared to previous approaches
| Study | Feature selection | Hyperparameter optimization | Model | Accuracy (%) |
|---|---|---|---|---|
| Hassan et al. [23] | PCA | - | LR | 93.33 |
| Valarmathi and Sheela [9] | - | Grid search, randomized search, and genetic programming | RF and XGBoost | 97.52 |
| El Sherbiny et al. [24] | - | - | NB, XGBoost, KNN, MLP, SVM, CatBoost | 94.34 |
| Narisetty et al. [25] | - | Grid-based solver with 10-fold cross-validation | LR | 90.1 |
| El-Ibrahimi et al. [26] | - | - | ANN, SVM, KNN, NB, DT | 96.6 |
| Our proposed method | IG | GA-based CNN | NB, SVM, DT, LR, RF | 100 |
PCA: principal component analysis, IG: information gain, GA: genetic algorithm, CNN: convolutional neural network, LR: logistic regression, RF: random forest, NB: naive Bayes, DT: decision tree, KNN: k-nearest neighbor, MLP: multilayer perceptron, SVM: support vector machine, ANN: artificial neural network.




 PDF
PDF Citation
Citation Print
Print



 XML Download
XML Download