서 론
직선성의 평가 및 설정
1. 직선성의 기본 개념
Fig. 1
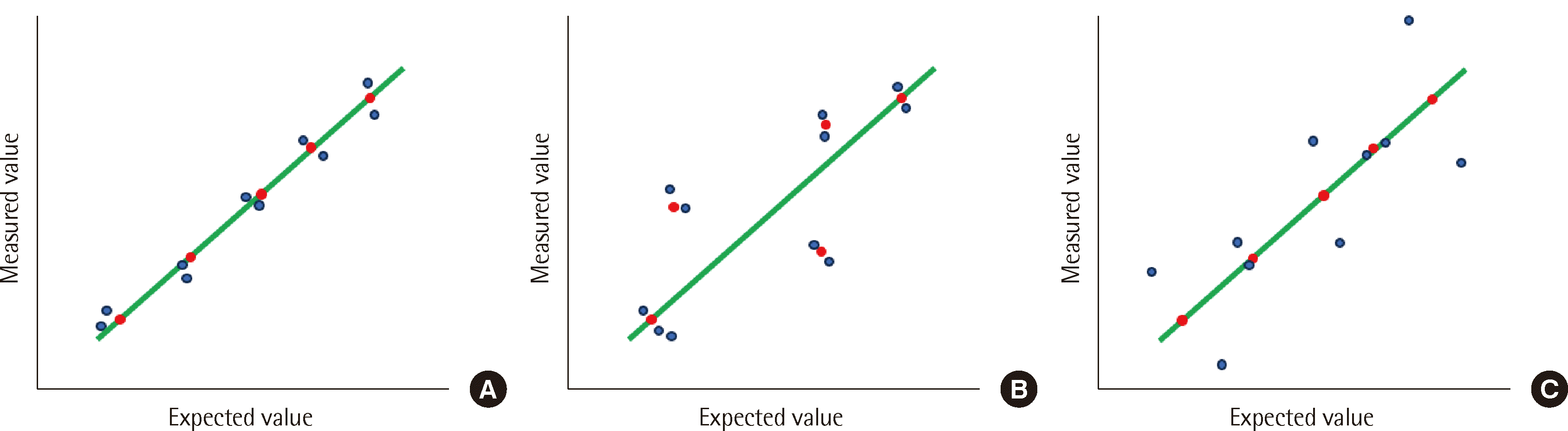
2. 직선성 평가법의 변천 과정
Table 1
| Variable | EP06-A (2003) | EP06-ED2 (2020) |
|---|---|---|
| Validation and verification | Not clearly separated | Clearly separated |
| Requirements for validation | 7–11 samples and 2–4 replicates | 9 samples (recommended) and at least 4 replicates |
| Requirements for verification | 5–7 samples and duplicates | At least 5 samples and at least 2 replicates |
| Concentration ranges of samples | Not specified |
Validation: relatively specified according to LI and AMI Verification: differentiated according to the %CV |
| How to prepare linearity panels | Mixing the low and high-level samples by considering the ratio | Equal volume mixing, proportional mixing, or serial dilution |
| Method for analyzing the linearity* |
Best-fit polynomial regression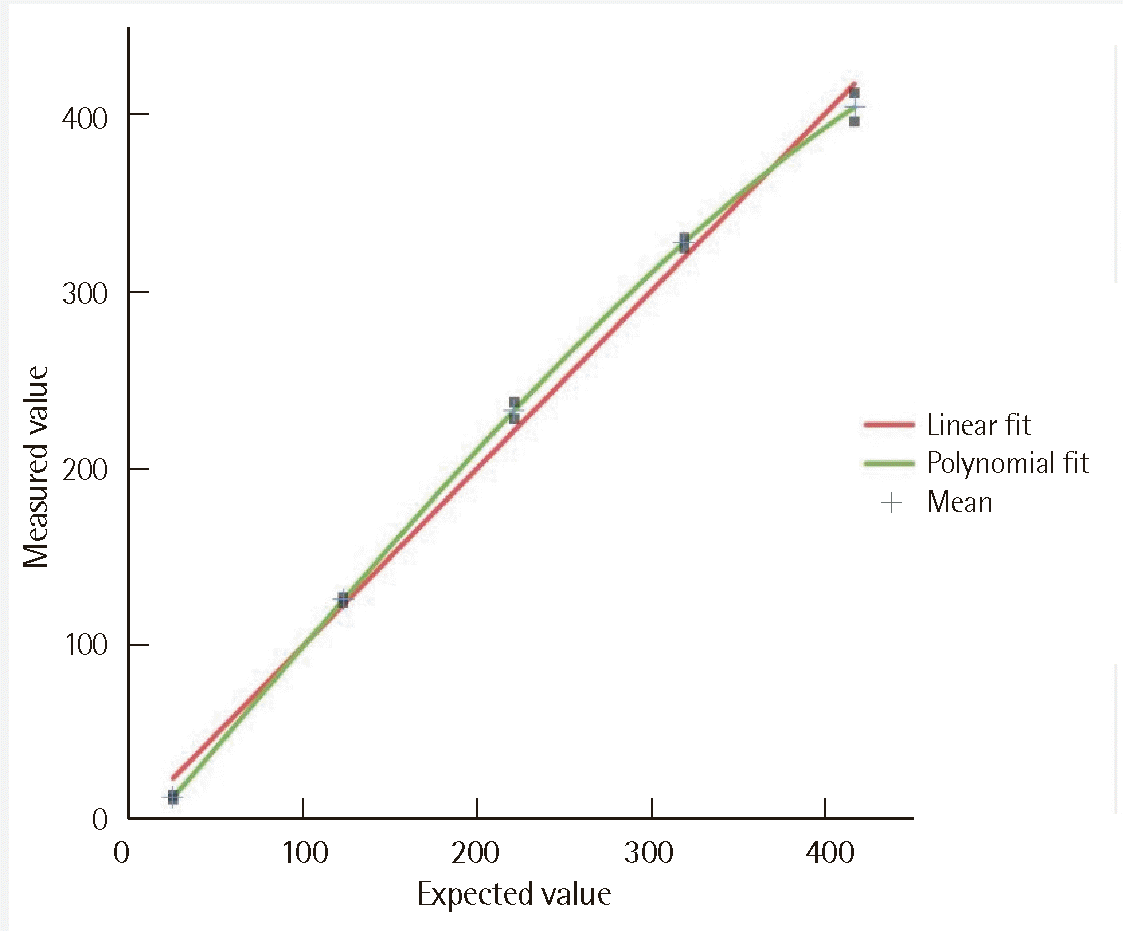
|
Weighted first-order (linear) regression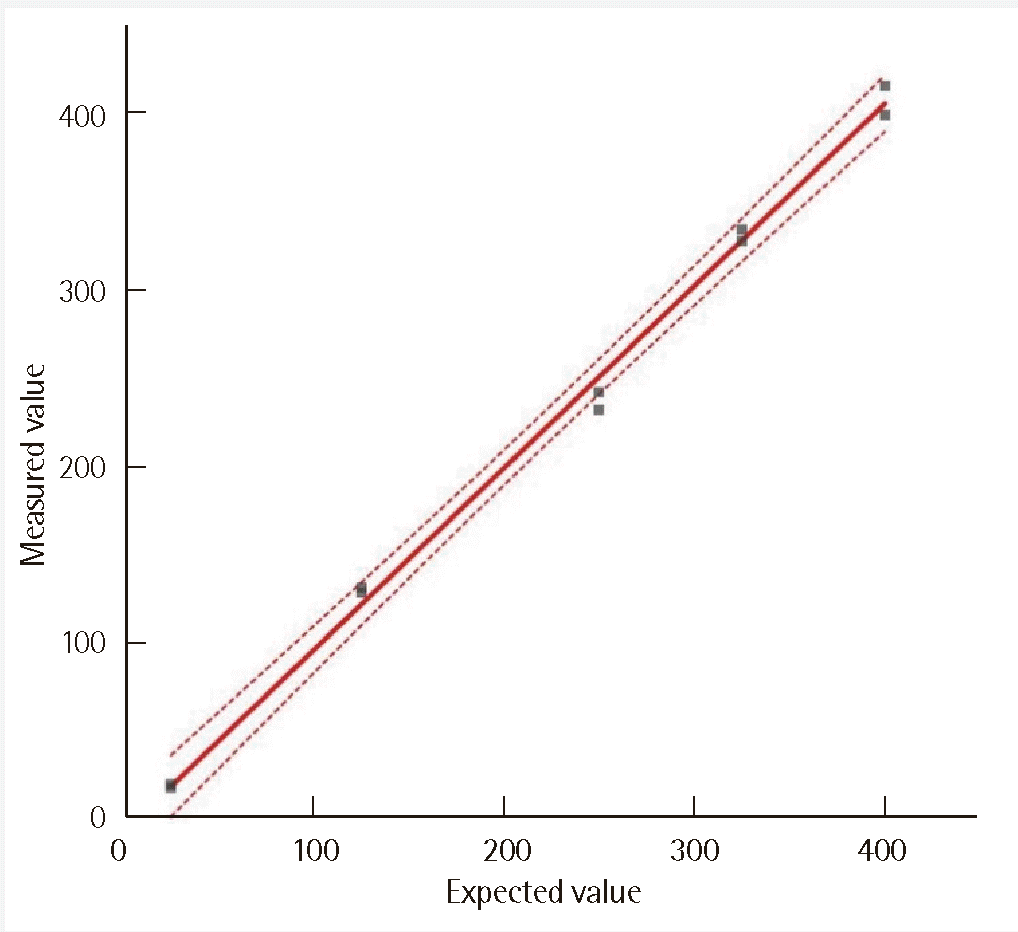
|
| Acceptance criteria |
|%bias|≤%target (or, absolute bias ≤absolute target in the low level) |
Validation: |%deviation|≤%ADL (%deviation: between measured mean value and predicted value after applying the weight) Verification: if any of the upper and lower limits of 90% CIs of the %deviation overlaps with ADL |
*The images were modified from the Laboratory Medicine, 6th ed. (Korean Society for Laboratory Medicine, 2021 [15]).
3. 직선성 관련 용어 정의
4. 직선성 평가의 기본 고려사항
Fig. 2
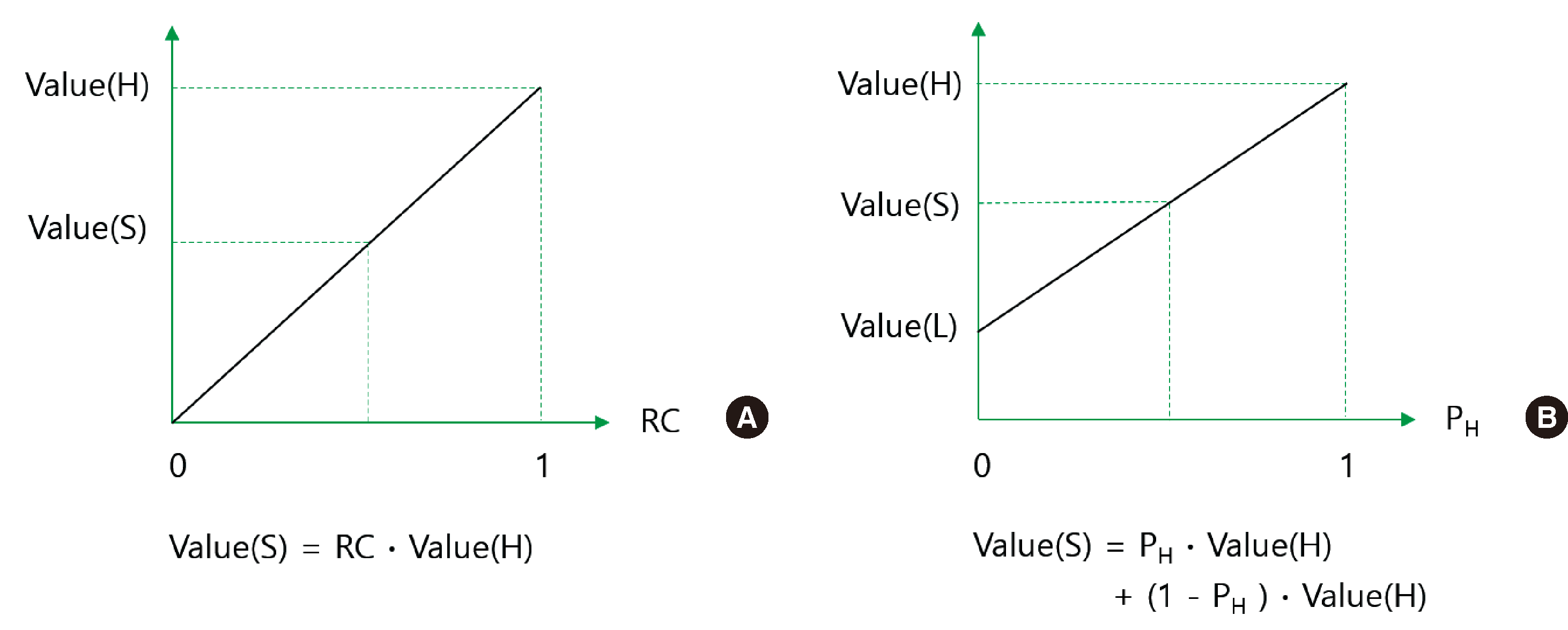
5. 직선구간의 검증
Fig. 3
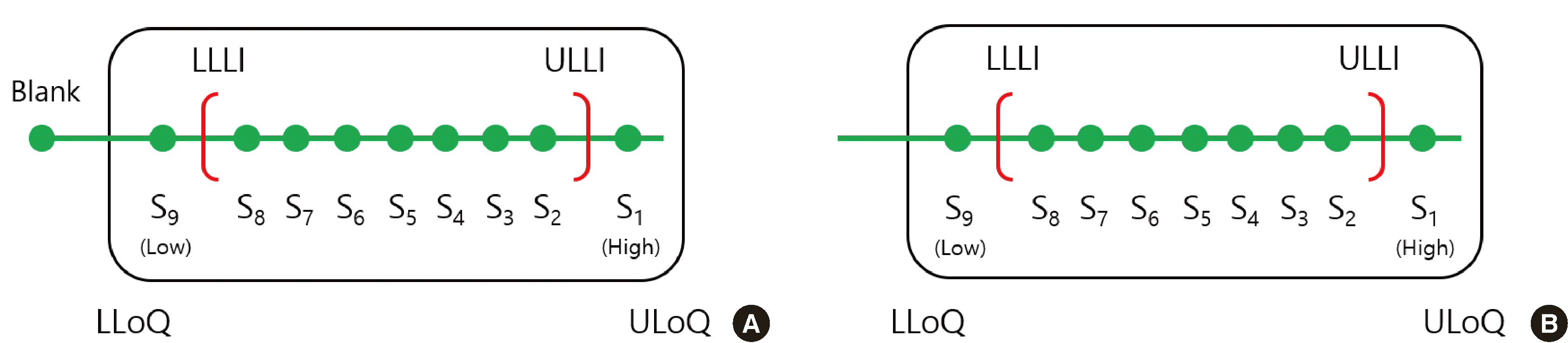
Table 2
| Level | RC | Measured value | Expected value (E)* | Weight (W)† | Product 1 W∙Y∙E | Product 2 W∙E2 | Predicted value (P)§ | Deviation|| | %Deviation¶ | Within ±ADL?++ | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| #1 | #2 | #3 | #4 | #5 | Mean (Y)** | SD | ||||||||||
| 1 | 1 | 550.1 | 547.7 | 555.4 | 557.6 | 541.1 | 550.38 | 5.84 | 550.38 | 0.1464 | 44,362.03 | 44,362.03 | 536.70 | 13.68 | 2.5 | Yes |
| 2 | 0.9 | 465.2 | 455.1 | 450.6 | 460.1 | 465.5 | 459.30 | 5.78 | 495.34 | 0.1495 | 34,013.66 | 36,682.77 | 483.03 | -23.73 | -4.9 | Yes |
| 3 | 0.75 | 412.5 | 406.3 | 401.1 | 412.3 | 398.5 | 406.14 | 5.70 | 412.79 | 0.1541 | 25,841.06 | 26,263.85 | 402.53 | 3.61 | 0.9 | Yes |
| 4 | 0.6 | 321.2 | 318.1 | 320.0 | 321.1 | 325.6 | 321.20 | 2.47 | 330.23 | 0.8218 | 87,170.64 | 89,620.75 | 322.02 | -0.82 | -0.3 | Yes |
| 5 | 0.5 | 270.1 | 277.6 | 266.1 | 268.1 | 271.2 | 270.62 | 3.90 | 275.19 | 0.3285 | 24,462.58 | 24,875.68 | 268.35 | 2.27 | 0.8 | Yes |
| 6 | 0.4 | 208.1 | 207.5 | 210.1 | 215.5 | 207.8 | 209.80 | 2.99 | 220.15 | 0.5585 | 25,797.53 | 27,070.43 | 214.68 | -4.88 | -2.3 | Yes |
| 7 | 0.25 | 135.8 | 130.1 | 131.1 | 134.5 | 136.9 | 133.68 | 2.65 | 137.60 | 0.7141 | 13,135.35 | 13,520.04 | 134.18 | -0.50 | -0.4 | Yes |
| 8 | 0.15 | 85.1 | 86.3 | 82.3 | 83.5 | 84.1 | 84.26 | 1.36 | 82.56 | 2.6847 | 18,675.51 | 18,298.05 | 80.51 | 3.75 | 4.7 | Yes |
| 9 | 0.08 | 48.5 | 47.6 | 45.5 | 47.5 | 43.0 | 46.42 | 1.97 | 44.03 | 1.2868 | 2,630.08 | 2,494.69 | 42.94 | 3.48 | 8.1 | Yes |
| 10 | 0.05 | 29.0 | 30.1 | 29.9 | 26.2 | 26.5 | 28.34 | 1.67 | 27.52 | 1.7944 | 1,399.46 | 1,358.91 | 26.84 | 1.50 | 5.6 | Yes |
| 11 | 0.03 | 16.5 | 14.5 | 15.0 | 16.6 | 17.1 | 15.94 | 1.01 | 16.51 | 4.9485 | 1,302.41 | 1,349.10 | 16.10 | -0.16 | -1.0 | Yes |
| SUM | >278,790.31 | >285,896.32 | ||||||||||||||
| A‡ | 0.9751 | |||||||||||||||
*Expected value (E): the calculated value using the value of the high-level sample and RC. E=RC∙Y; †W =R/(SD)2; ‡A=(Sum of Product 1)/(Sum of Product 2); §Predicted value (P): the value after applying the weight. P=A∙E; ||Deviation=Y–P; ¶%Deviation=100∙(Deviation)/P; **Mean (Y): mean of measured values for each level; ++If the ADL is 10% in this example, all of %deviation meets the goal.
6. 직선구간의 검정
Fig. 4
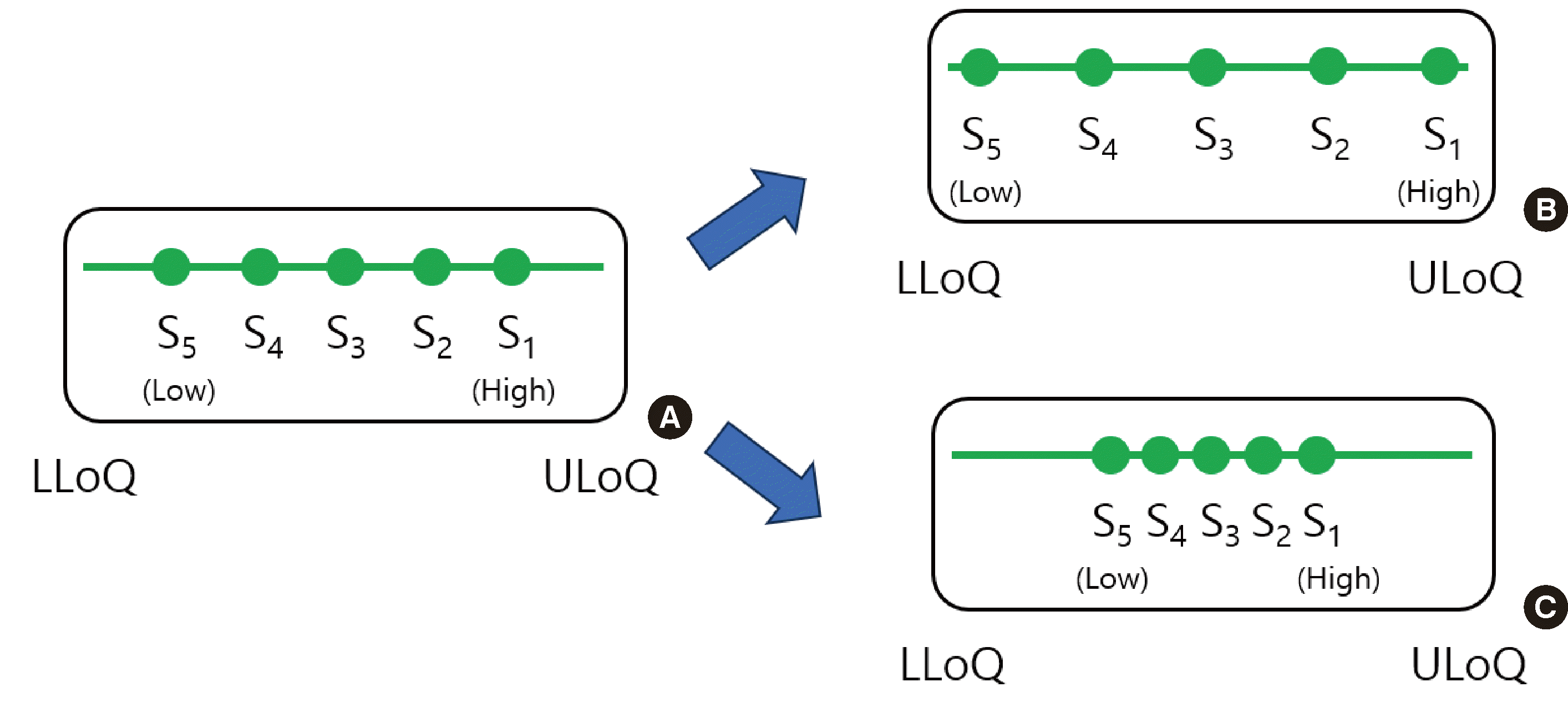
Fig. 5
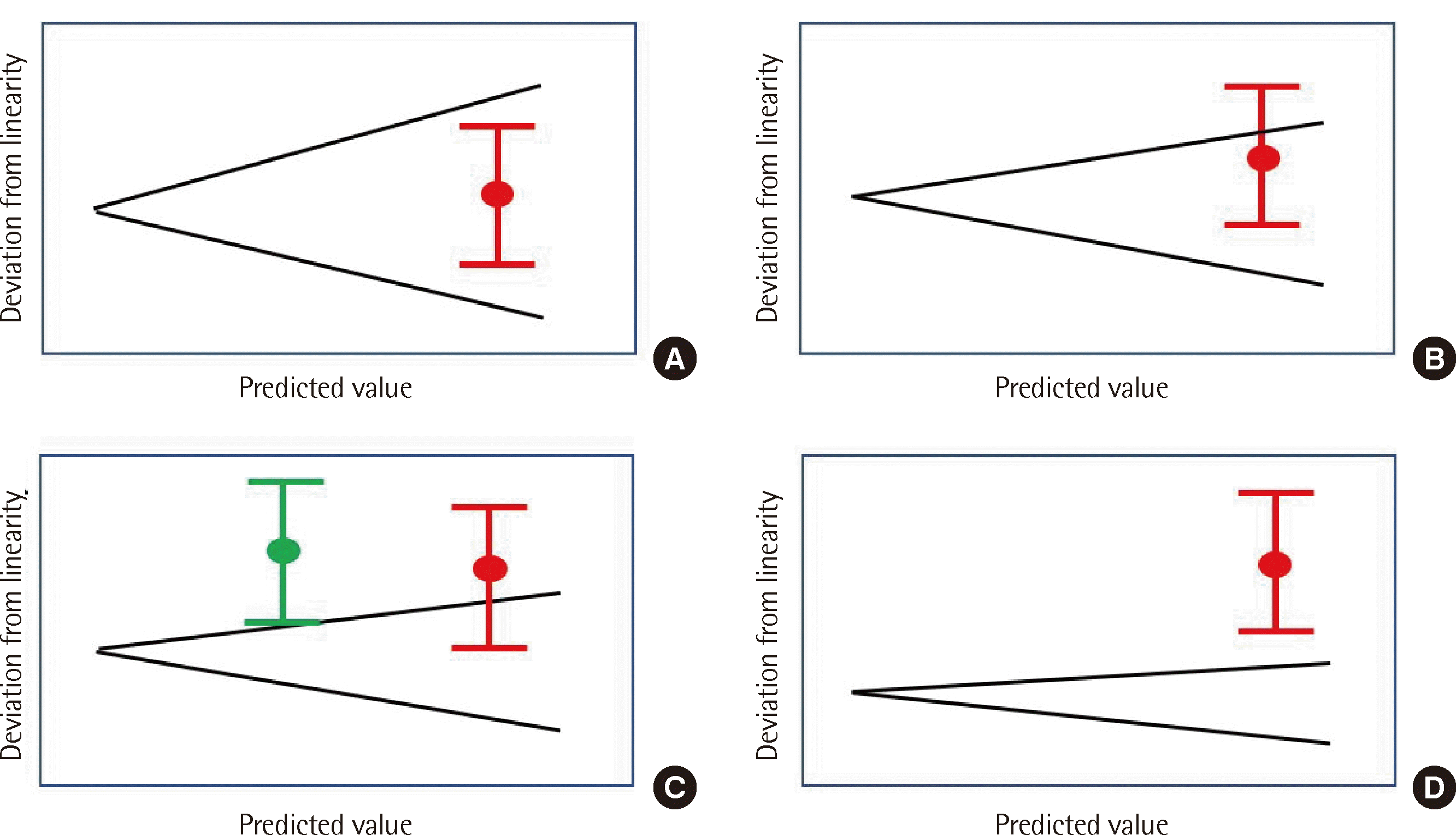
Table 3
When calculating the slope S using Microsoft Excel, use the command ‘LINEST((SD region), (M region),0)’ instead of the command ‘slope’ because it presupposes that there is a non-zero intercept.
When calculating the slope A using Microsoft Excel, use the command ‘LINEST((M region), (PH region)^2)’. And when calculating the intercept B using Microsoft Excel, use the command “SQRT(SUMSQ(Level 6 data)/3), where 3 is the number of replicates in this example.
확장측정구간의 평가 및 설정
1. 확장측정구간 관련 용어 정의 및 변천 과정
Fig. 6
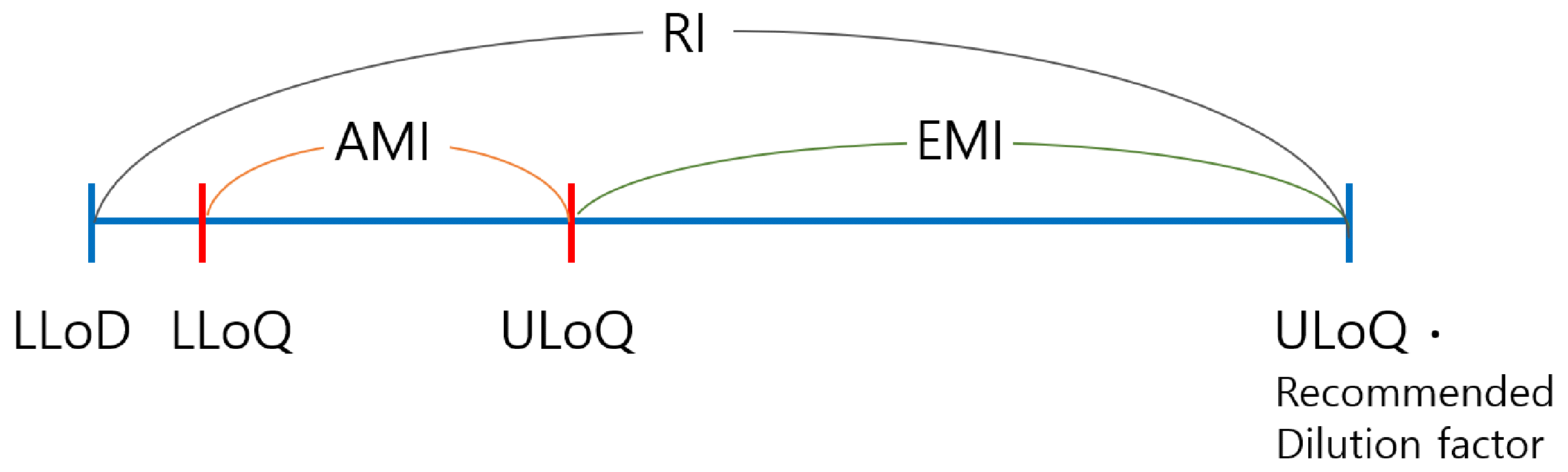
2. 희석배수 평가의 기본 고려사항
(1) ULoQ의 75–100%에 해당하는 농도의 검체를 사용하여 단계적으로 희석 후 각 농도에서의 비정밀도를 EP05 [42] 또는 EP15 [43]에 의거하여 평가하여 목표 변이계수 이상을 만족하는 최저 농도를 사전에 확립한다.
(2) 확립 이후에는 희석 평가에서 희석 후의 농도가 해당 최저 농도 이상이 되도록 희석 배수를 조정한다.
(3) 고농도의 검체를 희석한 샘플의 측정 결과가 LLoQ와 ULoQ 사이, 즉 AMI 범위 이내에 드는지를 확인한다.
(4) 후크효과(hook effect) 때문에 극히 높은 농도의 검체의 측정값이 AMI 이내의 값으로 측정되는 오류를 방지하기 위해서 최소 4개 이상의 검체를 이용하여 후크효과 여부를 평가하고 만일 후크효과가 발생 시 추가적인 희석 연구가 필요할 수도 있다.
(5) 추가적으로 부피 측정 오류로 인해 실제 의도한 희석배수와는 다른 희석이 이루어질 수 있는데, 계단 희석의 경우 부피 측정 오류를 줄일 수는 있으나 과정상 오류가 누적되어 한번에 높은 희석배수로 희석하는 것보다 오류가 더 크게 발생할 가능성이 있으니 주의해야 한다.
3. 희석배수의 설정
Table 4
Target value=(Value of neat sample)∙(Dilution factor); %Recovery=100∙(Observed value)/(Target value).
Mean and SD %Recovery are the values calculated using the %recoveries of 5 samples in each dilution factor.
From Appendix B of EP34-ED1 [19], the t-test value for N=5 is 2.776.
SE=SD/(√n); Upper 97.5% CL=mean %recovery+SE∙(t-test value); Lower 2.5% CL=mean %recovery–SE∙(t-test value).
If the goal of %recovery is 10%, the mean %recovery for all dilution factors satisfies the goal. However, in this example, the 97.5 upper CL or the 2.5 lower CL in 1/10 and 1/20 dilutions do not satisfy the goal. Therefore, 1/10 and 1/20 dilution factors cannot be used, and the maximum dilution factor established is 1/4.
4. 첨가 회수율 연구
Table 5
This example was extracted from the 1st edition of ‘Practical Handbook of Laboratory Medicine’ [16].
For example, when 0.05 mL of a 40-mg/dL spiking solution is added to 0.95 mL of serum, the added concentration of analyte is 40∙(0.05/1)=2 mg/dL.
Perform multiple measurements on each test sample (samples spiked with pure solvent, and samples spiked with spiking solution), and calculate the difference between the sample spiked with spiking solution and the sample spiked with pure solvent. In this example, the %recovery=100∙(calculated difference) / (expected difference), and the expected difference is 2 mg/dL. Then, compare the mean %recovery to the target %recovery.




 PDF
PDF Citation
Citation Print
Print

 XML Download
XML Download