Abstract
This study compared the dose calculated using the electron Monte Carlo (eMC) dose calculation algorithm employing the old version (eMC V13.7) of the Varian Eclipse treatment-planning system (TPS) and its newer version (eMC V16.1). The eMC V16.1 was configured using the same beam data as the eMC V13.7. Beam data measured using the VitalBeam linear accelerator were implemented. A box-shaped water phantom (30×30×30 cm3) was generated in the TPS. Consequently, the TPS with eMC V13.7 and eMC V16.1 calculated the dose to the water phantom delivered by electron beams of various energies with a field size of 10×10 cm2. The calculations were repeated while changing the dose-smoothing levels and normalization method. Subsequently, the percentage depth dose and lateral profile of the dose distributions acquired by eMC V13.7 and eMC V16.1 were analyzed. In addition, the dose-volume histogram (DVH) differences between the two versions for the heterogeneous phantom with bone and lung inserted were compared. The doses calculated using eMC V16.1 were similar to those calculated using eMC V13.7 for the homogenous phantoms. However, a DVH difference was observed in the heterogeneous phantom, particularly in the bone material. The dose distribution calculated using eMC V16.1 was comparable to that of eMC V13.7 in the case of homogenous phantoms. The version changes resulted in a different DVH for the heterogeneous phantoms. However, further investigations to assess the DVH differences in patients and experimental validations for eMC V16.1, particularly for heterogeneous geometry, are required.
In 2022, the Varian Eclipse treatment-planning system (TPS) at our institution was upgraded to the latest version of 16.1 from the older version of 13.7. However, after the TPS versions were upgraded, users were required to confirm whether the doses calculated using the new version of the TPS with same commissioning beam data used in the old version yielded acceptable results for use in clinical treatment plans. Because the old version of the TPS had already been validated through comparisons of its dose calculations with measured data [1], to test the new version, users can simply compare the dose calculated using the new version of TPS with that calculated using the old version. Following the dose comparison between both versions of the TPS, any further improvement in the accuracy of the dose calculation owing to the version change can also be investigated by comparing the calculated dose with the upgraded version and the obtained measurements. This technical note is focused solely on the comparisons of the dose calculation of electron beams using the electron Monte Carlo (eMC) dose calculation algorithm for the new (eMC V16.1) and old (eMC V13.7) versions. Previous studies [2,3] and documents [4,5] have reported the accuracy and limitations of eMC, and these are beyond the scope of this technical note. Although the documents written by the manufacturer used almost the same descriptions to explain the eMC algorithms between the two versions [4,5], we compared the percentage depth dose (PDD) and lateral dose profile calculated for the homogeneous water phantom and lung/bone–inserted heterogeneous phantom using eMC V16.1 and eMC V13.7.
Box-shaped 30×30×30 cm3 water and bone phantoms were generated in the Eclipse TPS (Figs. 1a, b). Because the dose calculated by the eMC V13.7 was normalized to 100% at the maximum dose of the field central axis, we adopted the "Central Axis Dmax" normalization method in eMC V16.1 to perform a fair comparison. The commissioning beam data of VitalBeam (Varian Medical Systems), which was used for beam configuration of eMC V13.7, were also used to configure eMC V16.1. We used electron energies of 6, 9, 12, and 16 MeV with various field sizes (from 6×6 cm2 to 20×20 cm2) for the calculation. In particular, we used 12-MeV electron beams to irradiate the bone and lung phantoms. The planned dose per fraction was 100 cGy for all calculations. To calculate the electron dose distribution using the eMC, no normalization was applied, and the dose distribution was calculated using the eMC algorithm without any scaling of the dose distribution (i.e., denoted as "No Plan Normalization"). We selected "No Plan Normalization" in plan normalization mode for both versions. Two options for smoothing the dose distribution are available in the eMC algorithm. The irregularities in the dose distribution were smoothed out and the dose distributions were convolved using a three-dimensional (3D) Gaussian kernel. Furthermore, two-dimensional (2D) median smoothing was used to replace the dose points of interest with the median dose values in the vicinity of the surrounding regions of these points. The level of smoothing could be from low to high (denoted as "low", "medium", and "strong"). We adopted 3D Gaussian smoothing in this study because this method has been applied to clinical cases at our institution. Subsequently, we repeated the calculations by changing the smoothing levels from "low" to "medium" and "strong", with the method of smoothing fixed as a 3D Gaussian. In addition, "no smoothing" dose distributions were calculated. For each eMC version, we compared the PDD curves and lateral dose profiles with "no smoothing" and 3D Gaussian smoothing. The depth for the lateral dose profiles for each electron energy was the depth at the maximum dose on the central axis for 3D Gaussian "low" and "medium" level smoothing calculated using eMC V13.7. Furthermore, the calculation with the exact same setup was repeated twice to show the extent to which statistical uncertainties can affect the PDD curves and lateral profiles. To evaluate the dose-volume histogram (DVH) difference owing to the version change, we used the dose calculated with 3D Gaussian "medium" level smoothing to compare the two versions, because it has been used in clinical practice at our institution. The volumes of interest (VOIs) are shown in Figs. 1a, b. The minimum dose (Dmin), maximum dose (Dmax), mean dose (Dmean), dose receiving 2% of the VOI (D2), dose receiving 50% of the VOI (D50), dose receiving 98% of the VOI (D98), and homogeneity index (HI; D2–D98/D50) were evaluated. Furthermore, we defined statistical uncertainty as 1% for each eMC calculation. Moreover, the calculation for each geometry was repeated 10 times and the statistical significance of the difference in dosimetric evaluation metrics was analyzed using an independent-sample t-test.
A 5×5×1 cm3 bone was inserted at a depth of 1 cm in a 30×30×30 cm3 water phantom, and a 5×5×1 cm3 lung was inserted at a depth of 1 cm in a 30×30×30 cm3 water phantom generated in the TPS (Fig. 1c). In addition, a heterogeneous phantom with bone and lung was generated, as illustrated in Fig. 1d. Furthermore, to calculate the dose in each heterogeneous phantom, we used 12-MeV electron beams with a 10×10 cm2 field with 3D Gaussian "medium" smoothing level. Consequently, the DVH difference in 2D dose distribution between the eMC V16.1 and eMC V13.7 was analyzed. Figs. 1c, d show the VOIs. Subsequently, we evaluated Dmin, Dmax, Dmean, D2, D50, D98, and HI (HI, D2–D98/D50). Moreover, to assess the difference in dose distribution due to statistical uncertainties, calculations for each eMC version were repeated 10 times (i.e., different initial seed numbers).
Figs. 2–5 show the PDD curves and lateral dose profiles of the 10×10 cm2 6- and 12-MeV electron beams against the water phantom calculated using eMC V13.7 with respect to the smoothing levels. The differences in the PDD curves and lateral profiles of 9 and 16 MeV between eMC V13.7 and eMC V16.1 were similar to those of 6 and 12 MeV. Thus, to avoid data redundancy, we report the results of the 6- and 12-MeV electron beams with a field size of 10×10 cm2. After applying "No Plan Normalization" to the calculation, the maximum dose of the central axis was normalized to 100% for the 3D Gaussian "low" smoothing level. Furthermore, the monitoring unit was calculated to deliver 100 cGy to the point of a 100% dose. After determining the normalization point, "medium" and "strong" smoothing were applied to the "no smoothing" dose distribution. Therefore, the doses for the determined normalization dose point with a "low" smoothing level were lower than 100 cGy in "medium" and "strong" smoothing. Similar characteristics were observed for the lateral dose profiles. For homogeneous water phantoms, the PDD and lateral profiles were within the defined statistical uncertainty, as shown in Figs. 2g, h; 3g, h; 4g, h; 5g, h. Fig. 6 shows the DVH curves for each geometry. We considered the average of the 10 DVH curves for each eMC version. In the case of homogeneous phantoms, the DVH curves of the VOIs calculated using the two eMC versions exhibited minimal differences. The relative difference in the dosimetric evaluation metrics was within 0.7% (Table 1). However, in the heterogeneous bone and bone/lung mixed phantoms, relatively larger differences were observed than those in the homogeneous phantoms. Fig. 7 shows the PDD curves for each geometry. For heterogeneous phantoms, particularly in the bone, the PDD was higher in eMC V13.7 than that obtained using eMC V16.1. Systematic differences of up to 3.0% (D50 of lung in bone/lung mixed phantom) were observed in heterogeneous geometry. Further investigations are required to assess the DVH differences in patients and experimental validations for eMC V16.1, particularly for heterogeneous geometry.
The dose distribution calculated by eMC V16.1 was comparable to that calculated using eMC V13.7 for homogenous phantoms. The change in version resulted in a different DVH for the heterogeneous phantoms. However, there is a need for further investigations to assess the DVH differences in patients and experimental validations for eMC V16.1, particularly for heterogeneous geometry.
Acknowledgements
This work was supported by the Seoul National University Hospital (No. 0420220290).
Notes
Availability of Data and Materials
The data that support the findings of this study are available on request from the corresponding author.
Author Contributions
Conceptualization: Chang Heon Choi. Data curation: Jaeman Son, Seonghee Kang. Formal analysis: Hyeongmin Jin. Investigation: Seongmoon Jung. Methodology: Jong-Min Park, Jung-in Kim. Supervision: Chang Heon Choi. Validation: Jaeman Son, Seonghee Kang, Hyeonmin Jin. Visualization: Seongmoon Jung. Writing – original draft: Seongmoon Jung. Writing – review & editing: Chang Heon Choi.
References
1. Sung J, Jin H, Kim J, Park JM, Kim JI, Choi CH, et al. 2020; Improvement of calculation accuracy in the electron Monte Carlo algorithm with optional air profile measurements. Prog Med Phys. 31:163–171. DOI: 10.14316/pmp.2020.31.4.163.

2. Chamberland E, Beaulieu L, Lachance B. 2015; Evaluation of an electron Monte Carlo dose calculation algorithm for treatment planning. J Appl Clin Med Phys. 16:4636. DOI: 10.1120/jacmp.v16i3.4636. PMID: 26103470. PMCID: PMC5690146.

3. Aubry JF, Bouchard H, Bessières I, Lacroix F. 2011; Validation of an electron Monte Carlo dose calculation algorithm in the presence of heterogeneities using EGSnrc and radiochromic film measurements. J Appl Clin Med Phys. 12:3392. DOI: 10.1120/jacmp.v12i4.3392. PMID: 22088999. PMCID: PMC5718744.

4. Eclipse photon and electron algorithms reference guide. 2015. Varian Medical Systems, Inc;Palo Alto: P1008611-003-C.
5. Eclipse photon and electron algorithms reference guide. 2020. Varian Medical Systems, Inc;Palo Alto: P1044595-001-A.
Fig. 1
Geometry for electron Monte Carlo calculation. (a) Homogeneous water phantom, (b) homogeneous bone or lung phantom, (c) heterogeneous bone or lung phantom, and (d) heterogeneous bone and lung phantom.
Fig. 2
Percent depth dose (PDD) of 6-MeV electron beam calculation using (a) electron Monte Carlo (eMC) V13.7, (b) eMC V16.1, and (c) comparison between eMC V13.7 and eMC V16.1 using three-dimensional Gaussian "low" smoothing and (d) "medium" smoothing. (e–h) The PDD ranges from 70%–105% for (a), (b), (c), and (d). 3D, three-dimensional.
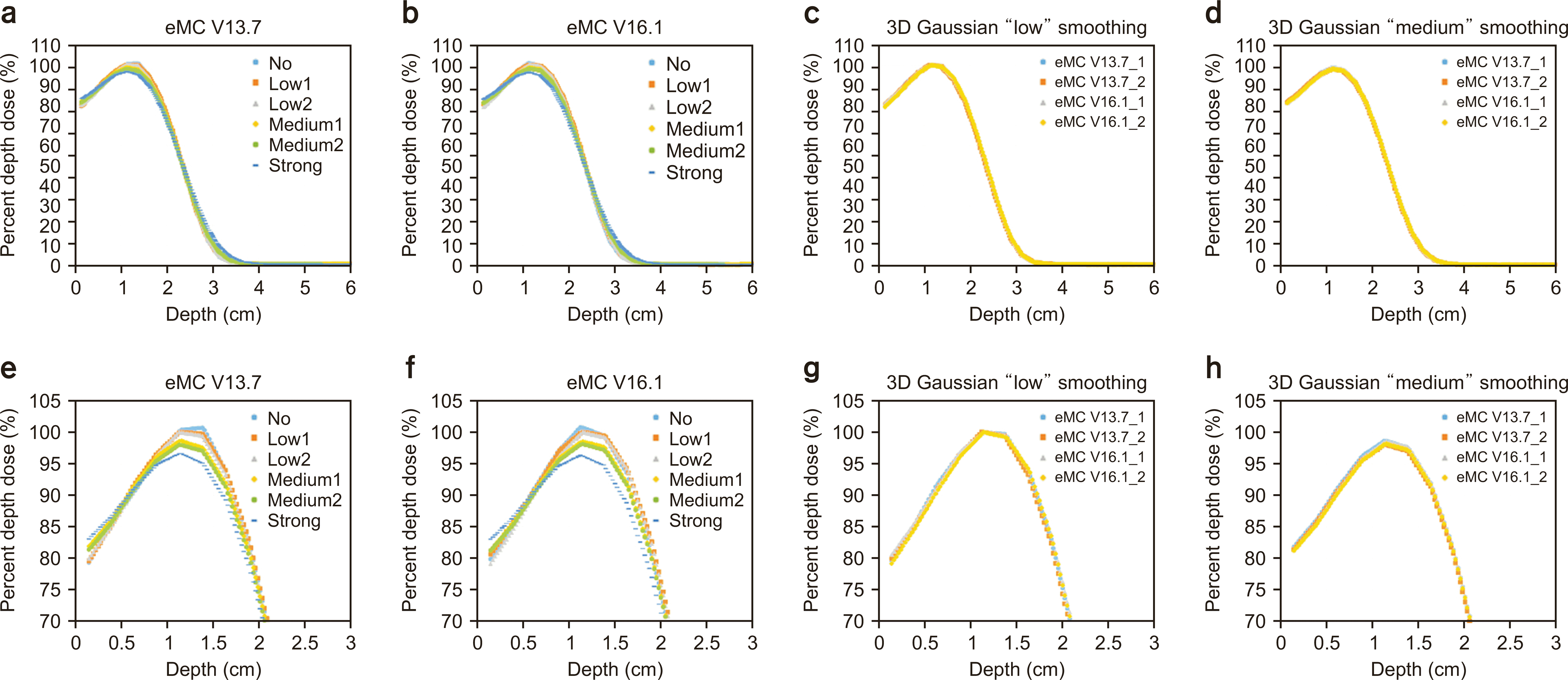
Fig. 3
Percent depth dose (PDD) of 12-MeV electron beam calculation using (a) electron Monte Carlo (eMC) V13.7, (b) eMC V16.1, and (c) comparison between eMC V13.7 and eMC V16.1 using three-dimensional Gaussian “low” smoothing and (d) “medium” smoothing. (e–h) The PDD ranges from 75%–105% for (a), (b), (c), and (d). 3D, three-dimensional.
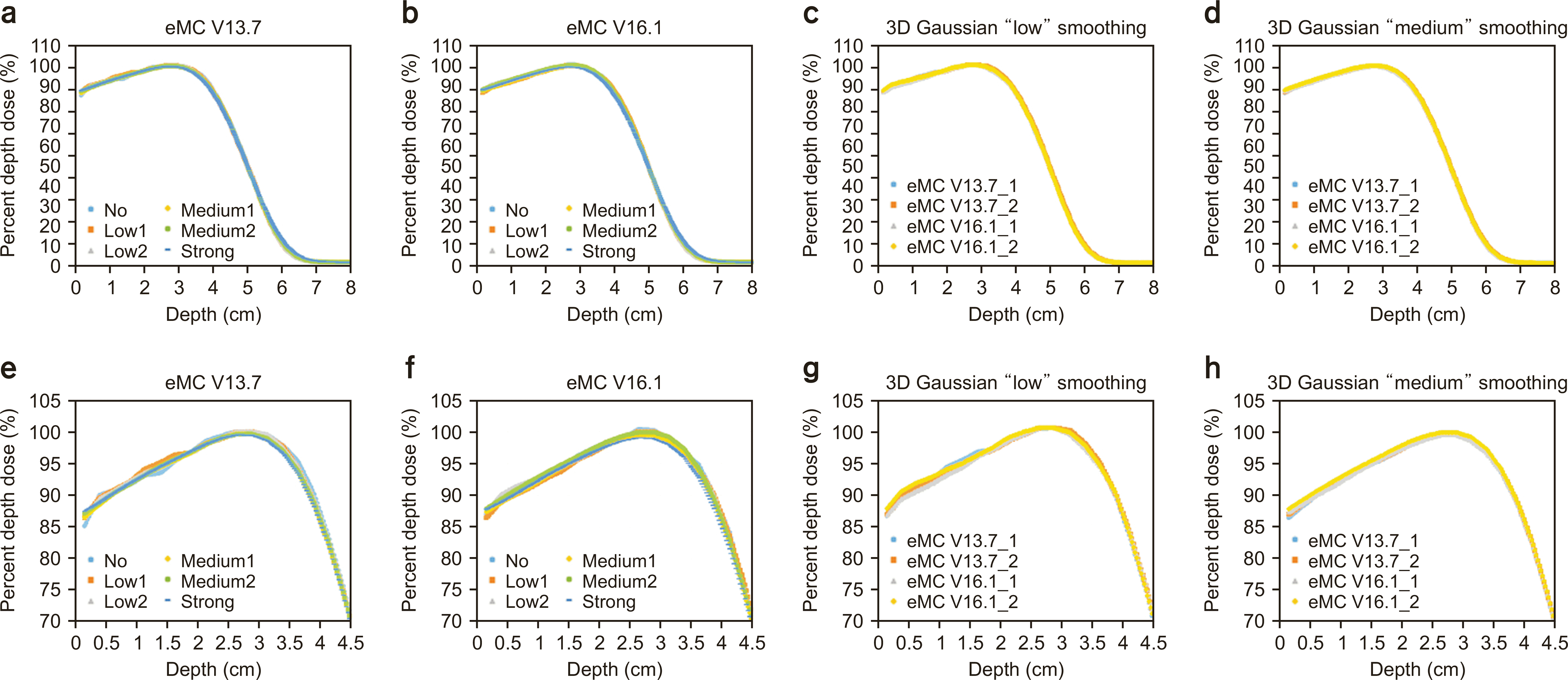
Fig. 4
Lateral dose profile of 6-MeV electron beam calculation using (a) electron Monte Carlo (eMC) V13.7, (b) eMC V16.1, and (c) comparison between eMC V13.7 and eMC V16.1 using three-dimensional Gaussian "low" smoothing and (d) "medium" smoothing. (e–h) The percent depth dose ranges from 80%–105% for (a), (b), (c), and (d). 3D, three-dimensional.
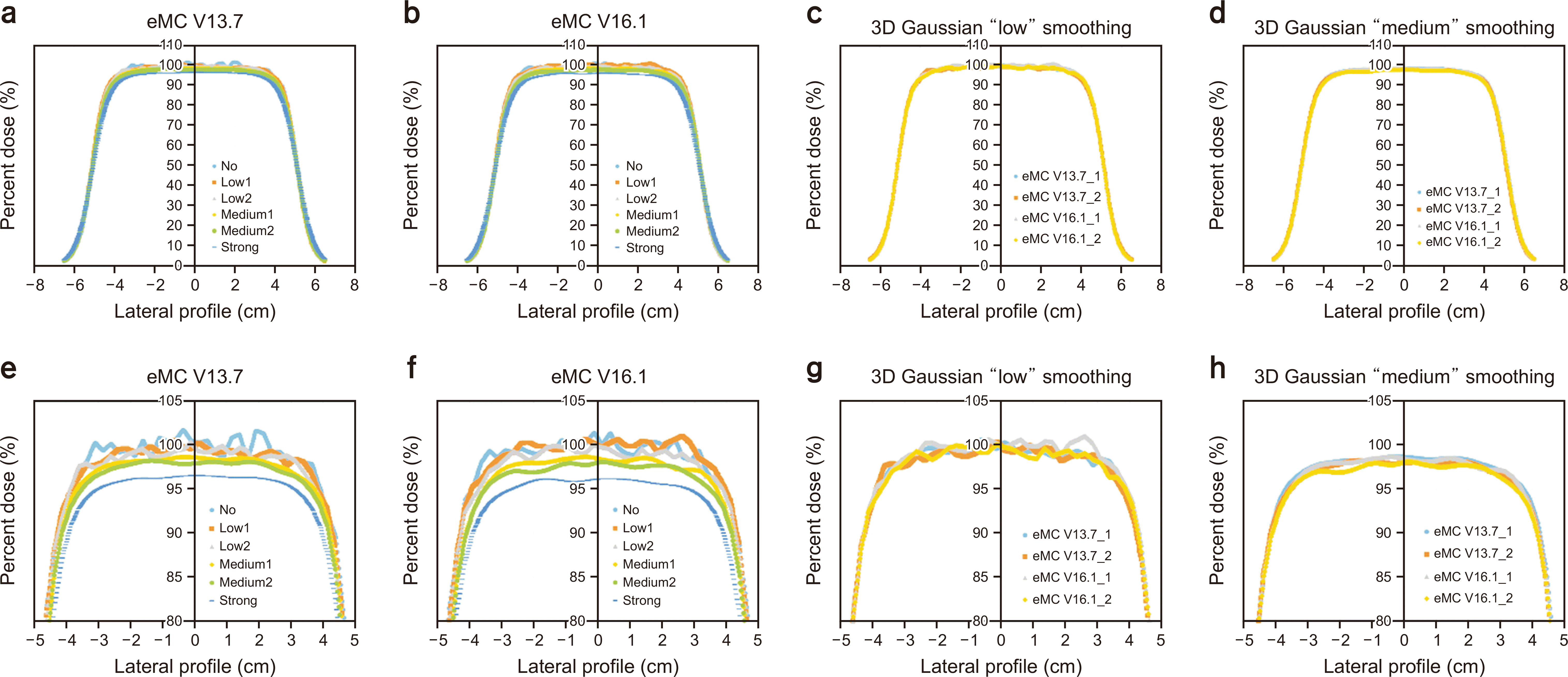
Fig. 5
Lateral dose profile of 12-MeV electron beam calculation using (a) electron Monte Carlo (eMC) V13.7, (b) eMC V16.1, and (c) comparison between eMC V13.7 and eMC V16.1 using three-dimensional Gaussian "low" smoothing and (d) "medium" smoothing. (e–h) The percent depth dose ranges from 80%–105% for (a), (b), (c), and (d). 3D, three-dimensional.
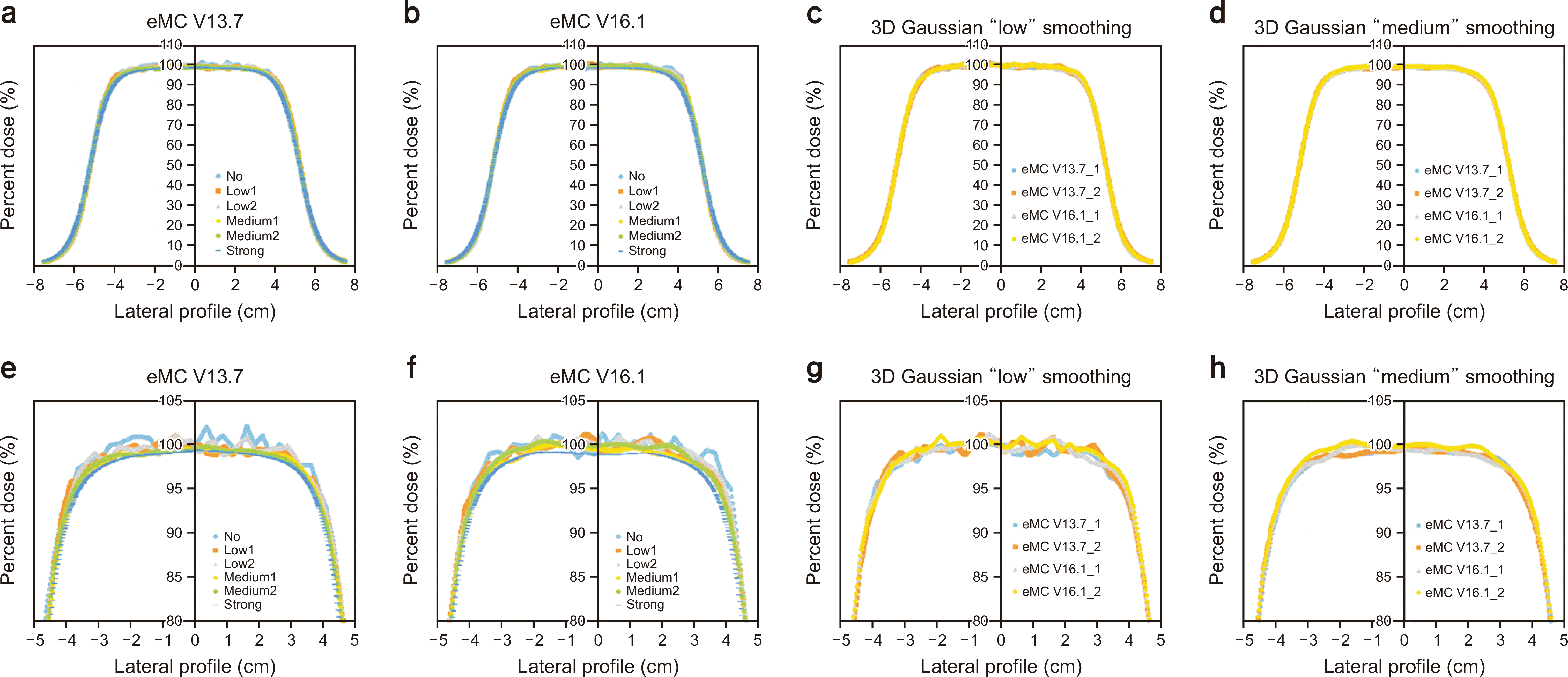
Fig. 6
Dose-volume histogram for each geometry calculated using electron Monte Carlo (eMC) V13.7 and eMC V16.1; (a) homogeneous water phantom (b) homogeneous bone phantom, (c) heterogeneous lung phantom (denoted as bone hetero), (d) heterogeneous bone phantom (denoted as lung hetero) and (e) bone and lung phantom (denoted as mixed hetero). VOI, volumes of interest.
Fig. 7
Percent depth dose for each geometry calculated using electron Monte Carlo (eMC) V13.7 and eMC V16.1: (a) homogeneous bone phantom, (b) heterogeneous bone phantom (denoted as bone hetero), (c) heterogeneous lung phantom (denoted as lung hetero), and (d) bone and lung phantom (denoted as mixed hetero).
Table 1
Dmin, Dmax, Dmean, D2, D50, D98, and homogeneity index (HI) of the electron Monte Carlo calculations for each geometry. Relative differences (RD) between eMC V13.7 and eMC V16.1 were calculated, and the statistical significance was also evaluated




 PDF
PDF Citation
Citation Print
Print



 XML Download
XML Download