PDF
Citation
Print
INTRODUCTION
Class III skeletal malocclusion is a common clinical dental abnormality. Maxillary protraction promotes maxillary growth by simulating suture growth around the maxilla. Conventional facemask therapy inevitably leads to dental side effects such as maxillary incisor protrusion, molar distalization, and clockwise rotation of the mandible.1 Several researchers have attempted to use facemasks with temporary anchorage devices to eliminate side effects and obtain the maximum skeletal effect. Sar et al.,2 Cevidanes et al.,3 and Zhou et al.4 have applied titanium plates for maxillary protraction to achieve favorable maxillary protraction outcomes. However, traditional titanium plate surgery is associated with trauma and the risk of tooth root damage. A three-dimensional (3D)-printed individual titanium plate was designed based on the surface morphology of the individual bone tissue, cortex bone thickness, and root distribution location. The titanium plate perfectly matched the cortical bone of the implant area and was positioned away from the root of the tooth.5,6
The 3D finite element method can be employed to analyze the distribution pattern of stress and possible biomechanical changes after loading. However, limited finite element studies have been conducted on maxillary protraction using miniplates. The locations of the miniplates and directions of the orthopedic forces varied in each experiment. Despite these variations, no study has presented sufficient evidence to support this hypothesis. Additionally, the impact of miniplate height on maxillary protraction has not been previously reported. Therefore, individual titanium plates were designed in different areas based on root distribution and bone condition.
To explore the underlying mechanics, a finite element model of maxillary hypoplasia, including the suture, was established. The stress distribution characteristics under different traction directions and miniplate heights were analyzed to provide a theoretical basis for the clinical application of maxillary protraction using an individual titanium plate.
Go to : 
MATERIALS AND METHODS
Finite element model construction
A 3D finite element model was developed using cone-beam computed tomography (CBCT) (slice thickness of 0.250 mm) scan data from an 11-year-old boy diagnosed with maxillary hypoplasia. The hand-wrist radiograph indicated a growth peak, identified by the appearance of the medial seed bone of the thumb and the epiphytic caps on the epiphyses of the middle and radius segments of the third section of the thumb. This study was approved by the Institutional Review Board (IRB) of the Beijing Stomatological Hospital, Capital Medical University (IRB number: CMUSH-IRB-KJ-PJ-2017-04F). The CBCT data were processed using Mimics software (version 15.01; Materialise, Leuven, Belgium), resulting in geometric models of each bone block in the stereolithography (STL) file format through threshold segmentation and 3D reconstruction. Following bone segmentation, adjacent sections were selected slice-by-slice to reconstruct the suture model. Three-dimensional STL files of the bone tissue were then imported into Geomagic software (Geomagic Studio 2013; Raindrop Corp., Wilmington, NC, USA) for additional processing and the generation of a solid model. The shapes of the titanium plate and screws in the anterior tooth area were designed using Creo software (version 3.0; Parametric Technology Corp., Needham, MA, USA) based on the bone surface morphology. Subsequently, the designs were imported into Geomagic to further optimization and assembly in the specified maxillary position. Considering the root distribution, the titanium plate was positioned 4 mm below the pyriform aperture and 10 mm above the alveolar ridge crest. The thickness of each titanium plate was 1 mm, with a hook located on the labial side of the alveolar crest. The miniscrew implants were simplified to a cylindrical shape (1.3 × 6 mm), and the cortical bone thickness at the implant site was approximately 1.5 mm. The Initial Graphics Exchange Specification files were imported into HyperMesh software (version 13.0; Altair Corp., Troy, MI, USA). The entire craniofacial complex model was assumed to be a continuous, homogeneous, isotropic, and linearly elastic material, with no division between cortical and cancellous bones. Referring to previous study, the material properties of the finite element model were defined, including those of cortical bone, suture line, titanium plate, and miniscrew (Table 1).7-9 Tetrahedral mesh division was utilized in the experiment. The finite element model comprised the cranial-maxillary complex and an individual titanium plate, consisting of 435,816 elements and 806,552 nodes (Figure 1). The model included nine defined sutures: frontomaxillary, bilateral zygomaticotemporal, zygomaticomaxillary, zygomaticofrontal, and pterygopalatine.
Boundary condition
The finite element model was imported into the Abaqus software (version 6.13; Dassault System, Vélizy-Villacoublay, France). An encastre boundary condition was imposed on the nodes around the foramen magnum and frontal bone to constrain all translational and rotational degrees of freedom in the X-, Y-, and Z-axes of those nodes.
All contact points in this experiment were treated as absolute static contact points. Completely staticity was observed both between the bones and titanium plate, as well as between the titanium plate and miniscrews, indicating an absence of relative sliding.
The 3D finite element analyses focused on the maxillary protraction using individual titanium plates at varying directions
A protraction force of 500 g per side was applied to the traction hook at forward and downward angles ranging from 0° to 60° relative to the Frankfort horizontal plane (Figure 2). The angle was increased in 10° increments. The von Mises stresses and the 1st principal stresses of the sutures were analyzed. The von Mises stresses provided a comprehensive overview of suture stress, whereas the 1st principal stress was utilized to determine the stress direction of the sutures. A linear graph and stress distribution nephogram were created based on the experimental data.
The 3D finite element analyses focused on the maxillary protraction using individual titanium plates at varying heights
In the 3D finite element analyses focusing on maxillary protraction with individual titanium plates at varying titanium plate heights, the titanium plate was displaced 2 and 4 mm upward and 2 and 4 mm downward. The position of the traction hook in the mouth remained relatively fixed. Therefore, we redesigned the titanium plate shape and adjusted the length of the hook arm to maintain the height of the force position (Figure 3). A force of 500 g was applied to the titanium plate hooks. In the third step of our experiment, the traction direction was selected to induce translational motion in the maxilla. The von Mises stresses and 1st principal stresses of the sutures were analyzed, and a linear graph and stress distribution nephogram were generated based on the experimental data.
Go to :
RESULTS
The 3D finite element analyses on maxillary protraction with individual titanium plates at varying directions
The von Mises stress
When a 500 g protraction force was applied at angles ranging from 0° to 60° relative to the Frankfort horizontal plane, the von Mises stresses in various sutures exhibited distinct patterns. The stresses in the pterygopalatine, zygomaticomaxillary, and zygomaticotemporal sutures decreased with an increasing protraction angle. For the frontomaxillary and zygomaticofrontal sutures, stresses initially decreased and subsequently increased, reaching a minimum value at a protraction angle of 40°. Among these, von Mises stresses were highest in the pterygopalatine and zygomaticotemporal sutures, whereas they were lowest in the zygomaticomaxillary suture (Figure 4).
 | Figure 4Linear graph and distribution nephogram of von Mises stress in sutures with varying protraction directions (protraction angle: from 0° to 60° with respect to the Frankfort horizontal plane). The colors in the stress distribution nephogram denote the magnitude of stress. The stress values increase as the color approaches red, whereas decreasing stress levels are indicated by colors closer to blue.
|
The 1st principal stresses in the pterygopalatine, zygomaticotemporal, and zygomaticomaxillary sutures exhibited positive values with an increase in the angle, with the pterygopalatine suture experiencing the highest stress levels. Conversely, the stress in the frontomaxillary suture was negative within an angle of 0° to 30°, decreasing as the angle increased. Between 30° and 40°, the stress transition from negative to positive, subsequently increasing by 40° to 60°. The stress pattern in the zygomaticofrontal suture showed positivity at angles of 0° to 40°, decreasing with an increase in the angle. Between 40° and 50°, the stress changed from positive to negative, becoming negative from 50° to 60°. However, the absolute value of the stress continued to rise with increasing angle. At an angle of 40°, the 1st principal stress of each suture was positive and exhibited a uniform distribution (Figure 5).
 | Figure 5Linear graph and distribution nephogram of the first principal stress in sutures with varying protraction directions (protraction angle: from 0° to 60° with respect to the Frankfort horizontal plane). The colors in the stress distribution nephogram represent the magnitude and direction of stress. As the color shifts toward red, it indicates increased tensile stress, whereas a shift toward blue signifies higher compressive stress.
|
The 3D finite element analyses on maxillary protraction with individual titanium plates at varying heights
Variation in von Mises stress distribution of each suture at varying protraction angles
The stress in each suture exhibited varying degrees of decrease with the downward movement of the titanium plate when a 500 g protraction force was applied at an angle of 40° relative to the Frankfort horizontal plane (Figure 6).
 | Figure 6Linear graph and distribution nephogram of von Mises stress in sutures with varying heights of titanium plates.
A, 4 mm upward movement; B, 2 mm upward movement; C, original position; D, 2 mm downward movement; E, 4 mm downward movement. The stress distribution nephogram reflects the magnitude of stress, with red indicating higher stress values and blue indicating lower stress levels.
|
Variation in the 1st principal stress distribution of each suture at varying titanium plate heights
During the downward movement of the titanium plate, the 1st principal stress in each suture remained positive. Notably, the stresses in the pterygopalatine and zygomaticotemporal sutures decreased, whereas the changes in the stresses in the zygomaticomaxillary, frontomaxillary, and zygomaticofrontal sutures were minimal (Figure 7).
 | Figure 7Linear graph and distribution nephogram of the initial principal stress in sutures with varying heights of titanium plate.
A, 4 mm upward movement; B, 2 mm upward movement; C, original position; D, 2 mm downward movement; E, 4 mm downward movement. The colors in the stress distribution nephogram depict both the magnitude and direction of stress. Intensity increases as the color shifts closer to red, indicating higher tensile stress. Conversely, as the closer the color approaches blue, the stress tends to be closer to zero.
|
Go to :
DISCUSSION
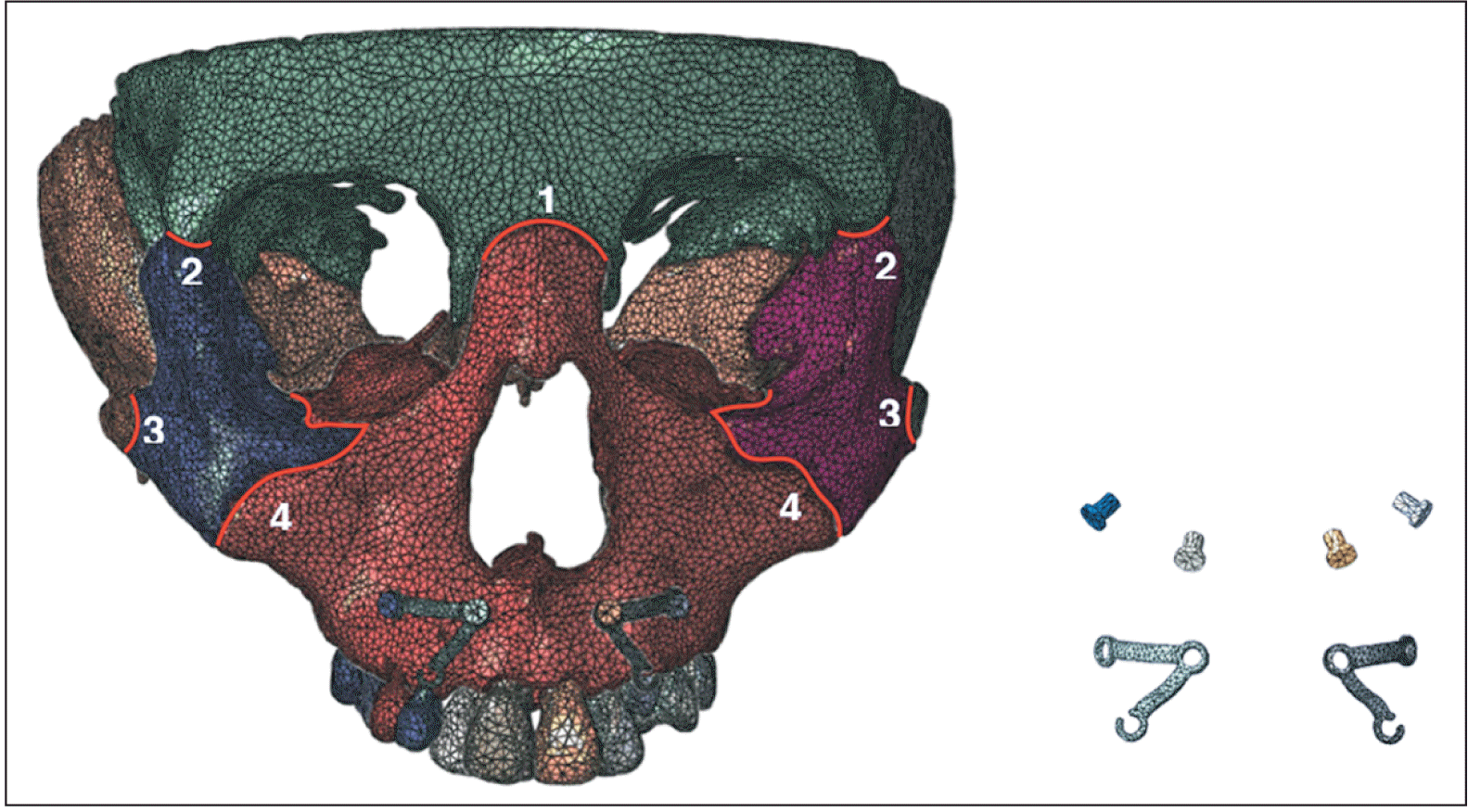
In a comparative analysis of maxillary protraction using a titanium plate in the zygomatic alveolar crest and lateral nasal wall areas, Lee and Baek8 observed greater stress values in the infrazygomatic crest. However, the titanium plate in the nasal sidewall area can reduce the counterclockwise rotation of the maxilla. Kim et al.10 revealed that maxillary protraction with the palatal plate resulted in a broader stress distribution, increased forward displacement, and a greater tendency for counterclockwise rotation than the miniplate at the infrazygomatic crest area and conventional tooth-borne appliances. For patients with Class III skeletal malocclusion, counterclockwise rotation of the maxilla is not conducive to improving the facial pattern. Therefore, in this study, titanium plates were placed in the anterior teeth. In traditional titanium plate surgery, a titanium plate is implanted into the lateral edge of the pyriform aperture to prevent damage to the root and permanent germ.11 However, this approach often results in severe trauma. The shape of the individual titanium plate and distribution of the titanium screws can be designed based on the CBCT data. Under the premise of avoiding damage to the root, an individual titanium plate can be implanted at the lower edge of the pyriform aperture to decrease surgical trauma and postoperative reactions. In this study, the range of vertical movement of the titanium plate was selected from the lower edge of the pyriform aperture to 6 mm above the alveolar crest, covering the clinical application range.
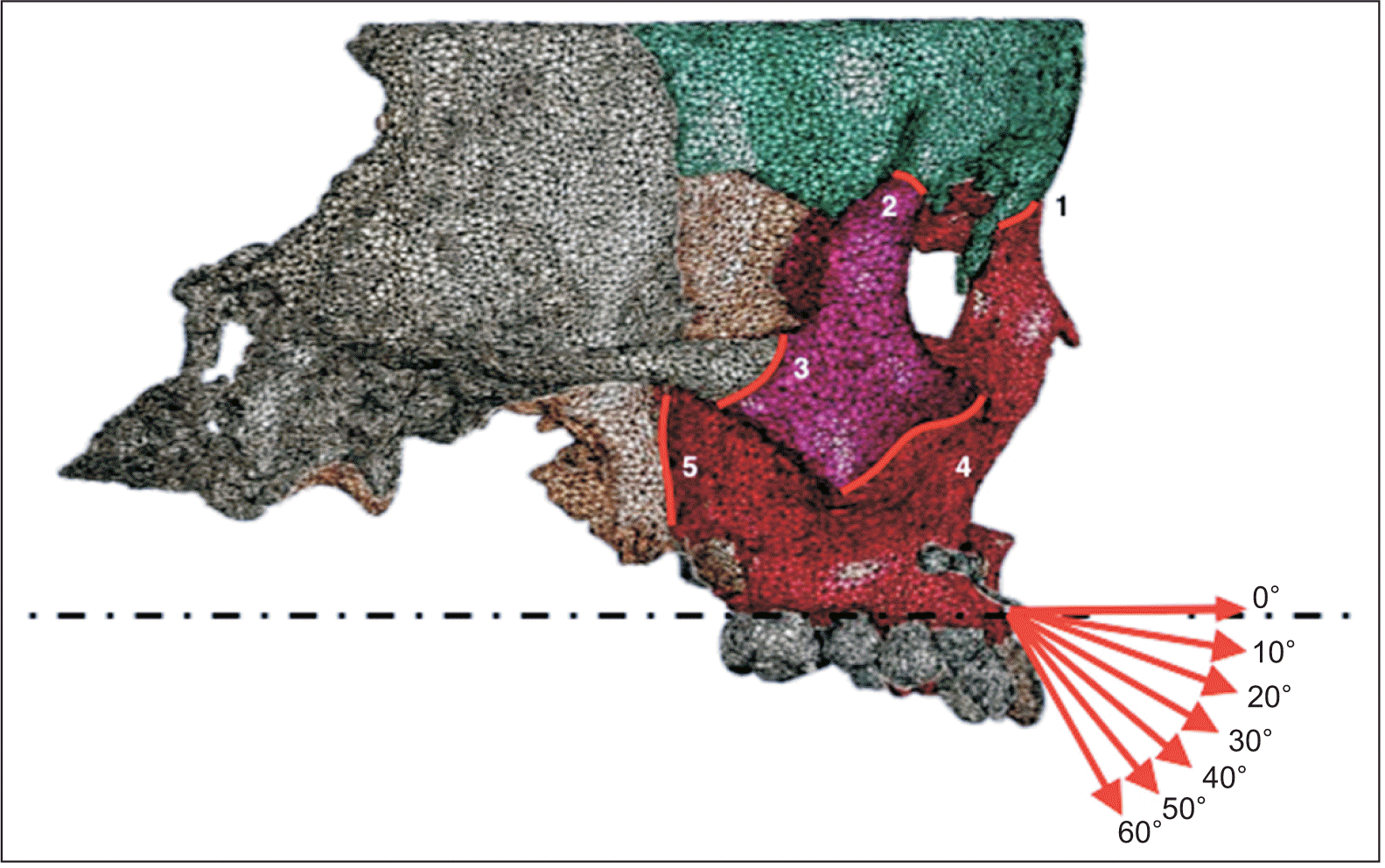
To determine the reference plane, previous studies, including the occlusal plane10,12 and Frankfort horizontal plane,13,14 were revisited. The occlusal plane, influenced by malocclusion severity and subject to significant variation among individuals, led us to choose the Frankfort horizontal plane as the reference.
Significant differences were observed in protraction force selection among prior studies. Lee and Baek,8 Yan et al.,15 and Zhang et al.16 utilized a force of 500 g per side to simulate maxillary protraction in their finite element models, whereas Tanne et al.,9 Miyasaka et al.,17 and Gautam et al.12 selected a force of 1,000 g. Zou and Lin18 reported that the von Mises stresses, maximum principal stresses, and displacement of the cranial-maxillary complex increased with higher protraction forces. However, orthopedic forces > 500 g per side resulted in an evident counterclockwise rotational tendency and narrowing of the dental arch in the maxilla, as observed in both clinical practice and previous studies. Based on this information, we chose a protraction force of 500 g for this study.
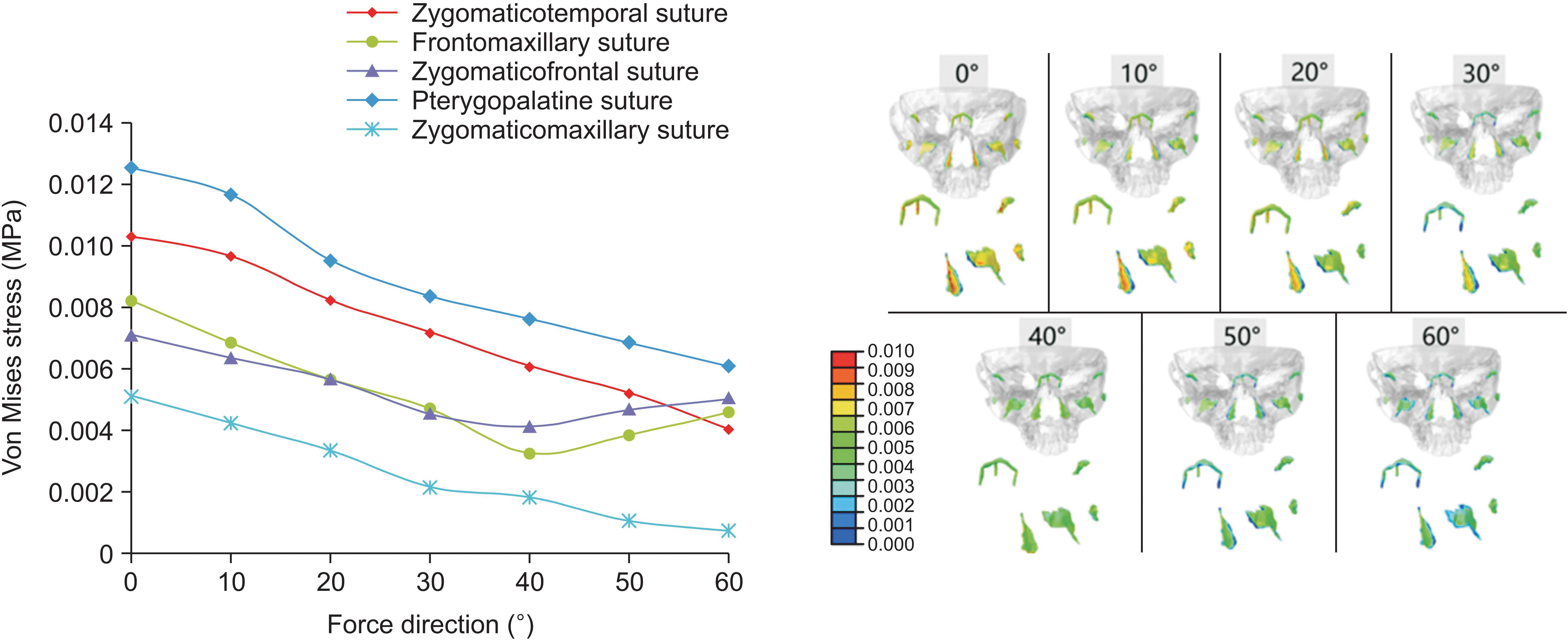
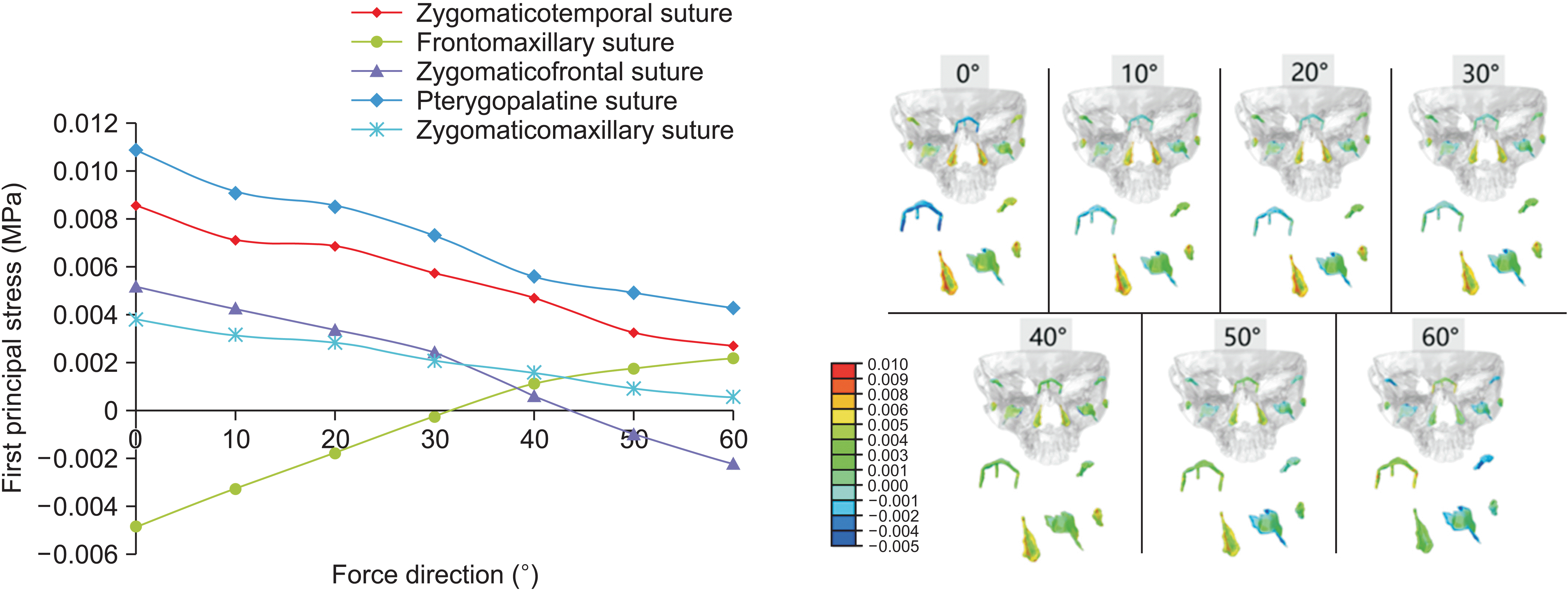
In the finite element analysis, each node was influenced by principal stresses in three directions, with the first principal stress having the largest absolute value among them. A negative value for the 1st principal stress indicates compressive stress in the sutures, whereas a positive value suggests tensile stress. Because the protraction force guides the growth direction of the maxilla, we focused on the first principal stress, representing the maximum traction force on the sutures used to analyze the growth direction of the maxilla. The frontomaxillary suture experienced compressive stress at a protraction angle of 0° to 30°, whereas the other sutures experienced tensile stress. Situated on the anterosuperior side of these sutures, the frontomaxillary suture showed a tendency for counterclockwise rotation in the maxilla. At a protraction angle of 40°, all sutures experienced tensile stress, indicating translational motion of the maxilla. Between a protraction angle of 50° and 60°, the zygomaticofrontal suture received compressive stress, whereas the other sutures received tensile stress. Positioned on the posterosuperior side of sutures, the zygomatic frontal suture indicated a tendency for clockwise rotation in the maxilla. The pterygopalatine, zygomaticotemporal, and zygomaticomaxillary sutures, distributed nearly longitudinally, generally experienced tensile stress under the horizontal component of maxillary protraction. For Class III patients with a deep overbite tendency, a protraction angle < 40° with respect to the Frankfort horizontal plane is recommended. Patients with a normal overbite may benefit from a protraction angle of approximately 40°, allowing translational movement of the maxilla along the translational direction. For Class III patients with an open bite tendency, an angle > 40° is suggested.
According to previous studies, Tanne et al.9 and Miyasaka et al.17 supported the idea that the optimal choice for maxillary protraction involves a forward and downward force angled at 30° with respect to the occlusal plane at the canines. The maxilla undergoes forward translation, and stress distribution is uniform. In this study, a titanium plate, chosen as the protraction device, was positioned at the lower edge of the pyriform aperture, causing its force point to move upward compared with that in the tooth anchorage, potentially influencing outcomes. Furthermore, prior studies did not construct a suture model and overlooked the significance of sutures in maxillary protraction. Yan et al.15 suggested translational motion of the cranial-maxillary complex when the force direction is approximately 20° relative to the occlusal plane during bone anchorage protraction, with bone anchorage at the infrazygomatic crest, which is not consistent with our findings. Qu et al.14 conducted maxillary protraction using an implant anchorage positioned between the lateral incisors and canines. They observed that the maxilla moved forward and rotated upward when the protraction angle was < 30°. At an angle of 40°, the suture in the nasion did not experience tensile or compressive stress, indicating translational motion of the maxilla. The maxilla moves forward and rotated downward when the angle exceeded 50°. The protraction loading position in this study was similar to that in Qu et al.,14 with both studies using the Frankfort horizontal plane as the reference plane. Therefore, our study results closely resemble those reported by Qu et al.14 This divergence might be attributed to the larger stress area of maxillary protraction with the titanium plate than the implant screws. Previous studies exhibited variations in maxillary protraction outcomes due to differences in finite element models, anchorage position, reference plane selections, and analysis indexes. In clinical applications, the direction of maxillary protraction should be determined based on the anchorage location and the vertical facial type of the patient.
In a 3D solid structure, the stress distribution is intricate and cannot be captured by a single directional stress value. The von Mises stress is often employed for heterogeneous objects with complex mechanical properties, including three principal stresses in directions equivalent to the same axis. The von Mises stresses of the pterygopalatine, zygomaticotemporal, and zygomaticomaxillary sutures decreased with an increasing protraction angle. The highest stress was observed when the force direction was approximately 0° with respect to the Frankfort horizontal plane. These results are consistent with those obtained by Yan et al.15 This consistency is attributed to the rough longitudinal distribution of the sutures. As the protraction angle increases, the component of the forward force gradually decreases, indicating that the protraction value should be appropriately increased with an increase in the protraction angle. The von Mises stresses on the frontomaxillary and zygomaticofrontal sutures initially decrease and then increase in accordance with the change in the 1st principal stress. In other words, the stress on the zygomaticomaxillary suture changes from negative to positive, whereas that on the zygomaticofrontal suture shows the opposite result.
Stress magnitude is influenced by several factors. First, stress magnitude is associated with the distribution of the sutures. The results showed higher stresses on the pterygopalatine and zygomaticotemporal sutures due to their vertical distribution and exposure to a greater forward component force. Secondly, stress is defined as the external force per unit area, correlating with the suture area. Kambara19 observed increased activity in the reconstruction of the zygomaticotemporal suture during maxillary protraction. The narrow shape of the suture led to stress concentration. Furthermore, stress is influenced by the distance from the protraction point and buffer during the force-transfer process. Therefore, stress magnitudes are the outcome of these combined factors.
Individual titanium plates were custom-designed based on bone thickness and root distribution, offering a range of options for implant height. The position of the traction hook in the mouth remained fixed, whereas the titanium plate was adjusted upward by 2 and 4 mm and downward by 2 and 4 mm. This study included various miniplate heights to encompass a broad spectrum of clinical scenarios. The analysis of stress distribution trends aimed to provide guidance for determining the optimal position of the titanium plate.
When the titanium plate moved downward, the von Mises stress of each suture decreased, albeit at varying amplitudes. This suggests an improvement in protraction efficiency with an increase in the titanium plate position. In clinical practice, when designing a titanium plate in a lower position, the force applied should be appropriately increased. The decrease in stress may be attributed to the increased distance between the application point and the sutures. Although this study designed the titanium plate with different heights, the position of the hooks remained constant. Therefore, factors such as hook length and angle variation could potentially contribute to these observed outcomes.
Throughout the movement of the titanium plate, the 1st principal stresses consistently exhibited positive values. This indicates that all sutures experienced tensile stress, resulting in translational motion of the maxilla. The findings suggest that the height of the titanium plate had an insignificant effect on maxillary rotation within the designed range. Therefore, in clinical applications, the choice of titanium plate position can be made based on considerations such as root distribution and bone mass.
This study had several limitations. The accuracy of the model was constrained by the thickness of the image layer. Additionally, the assumption of homogeneous, continuous, and isotropic bone tissue in the analysis deviates from the actual complex structure. Although finite element analysis offers insights for clinical applications, the influence of soft tissues such as muscles and ligaments on growth could lead to variations between experimental outcomes and real-world effects. The shape of an individual titanium plate can be customized based on various requirements, offering more choices for positioning. Further research is necessary to enhance guidance for the design of titanium plates.
Go to :
CONCLUSIONS
Various protraction directions are suitable for patients with different vertical bone surfaces. A protraction angle of 0° to 30° relative to the Frankfort horizontal plane is recommended for Class III patients with a deep overbite tendency. For patients with a normal overbite, a protraction angle of 40° is deemed suitable. Class III patients with an open bite tendency may benefit from a protraction angle of 50° to 60°.
When the titanium plate is placed at a lower position, the protraction force can be increased accordingly. Within this range, the impact of the height of the titanium plate on maxillary rotation was found to be less significant than that of the degree of protraction.
Go to :
XML Download