Introduction
Materials and Methods
Table 1
Table 2
The contents of this table were modified from the study by Lee et al. [25].
Table 3
| Model | Dental sextant combinations (types of teetha)) |
|---|---|
| 1 | All six sextants (all teeth excluding four third molars) |
| 2 | Maxillary and mandibular anterior sextants (11, 12, 13, 21, 22, 23, 31, 32, 33, 41, 42, 43) |
| 3 | Maxillary and mandibular, right and left posterior sextants (14, 15, 16, 17, 24, 25, 26, 27, 34, 35, 36, 37, 44, 45, 46, 47) |
| 4 | Maxillary anterior sextant (11, 12, 13, 21, 22, 23) |
| 5 | Mandibular anterior sextant (31, 32, 33, 41, 42, 43) |
| 6 | Maxillary right and left posterior sextants (14, 15, 16, 17, 24, 25, 26, 27) |
| 7 | Mandibular right and left posterior sextants (34, 35, 36, 37, 44, 45, 46, 47) |
| 8 | Maxillary right posterior sextant (14, 15, 16, 17) |
| 9 | Maxillary left posterior sextant (24, 25, 26, 27) |
| 10 | Mandibular left posterior sextant (34, 35, 36, 37) |
| 11 | Mandibular right posterior sextant (44, 45, 46, 47) |
a)The types of teeth were noted by FDI two-digit teeth designation system [26].
Results
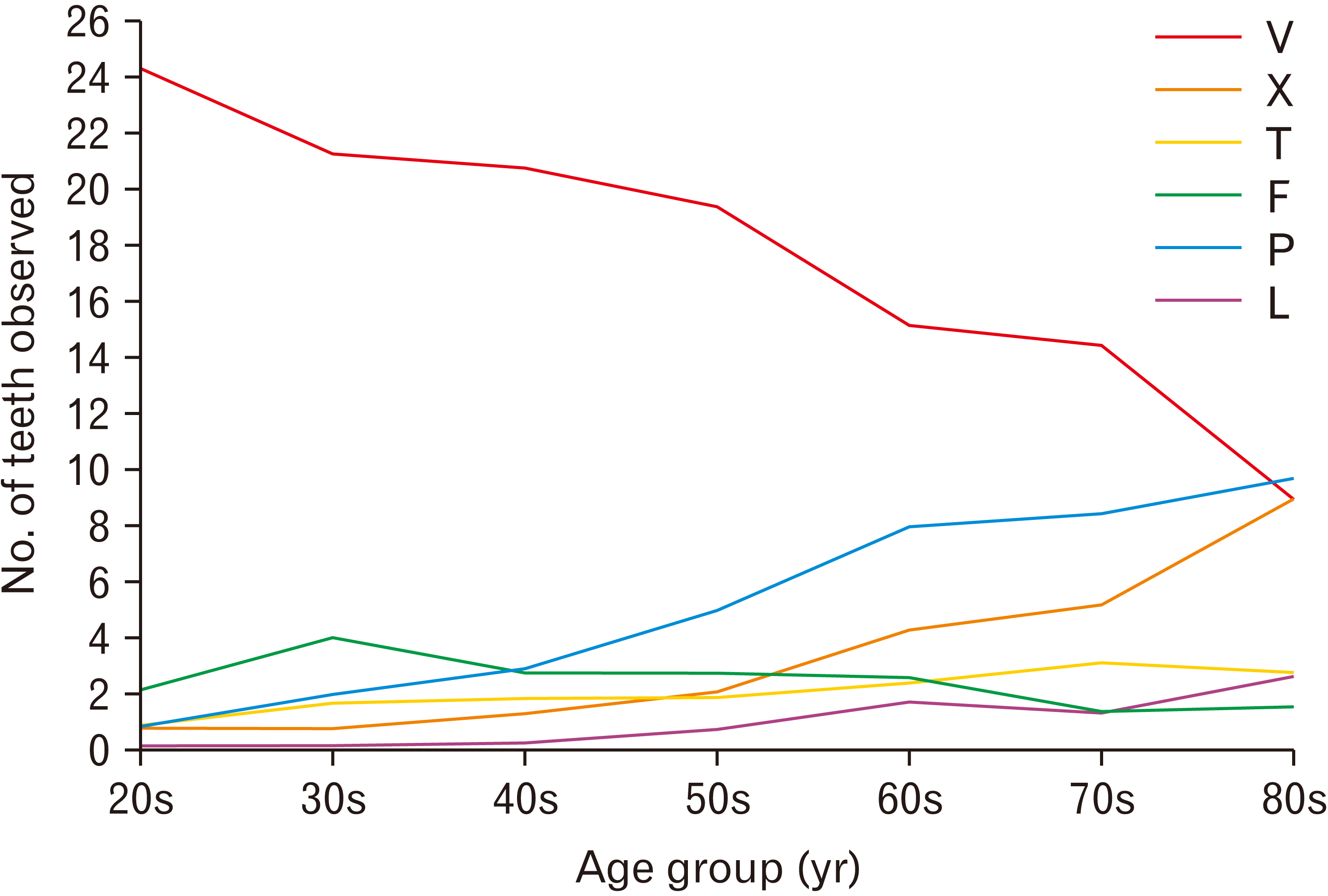 | Fig. 1Age-related changes in mean numbers of teeth by dental codes. The x-axis represents the age group (in years), and the y-axis represents the mean number of teeth observed. The definitions for each code are provided in Table 2. |
Table 4
Values are presented as mean±SD. The definitions for each code are provided in Table 2.
Table 5
The definitions for each code are provided in Table 2. NSC, number of subjects where the code was observed; TNS, total number of subjects.
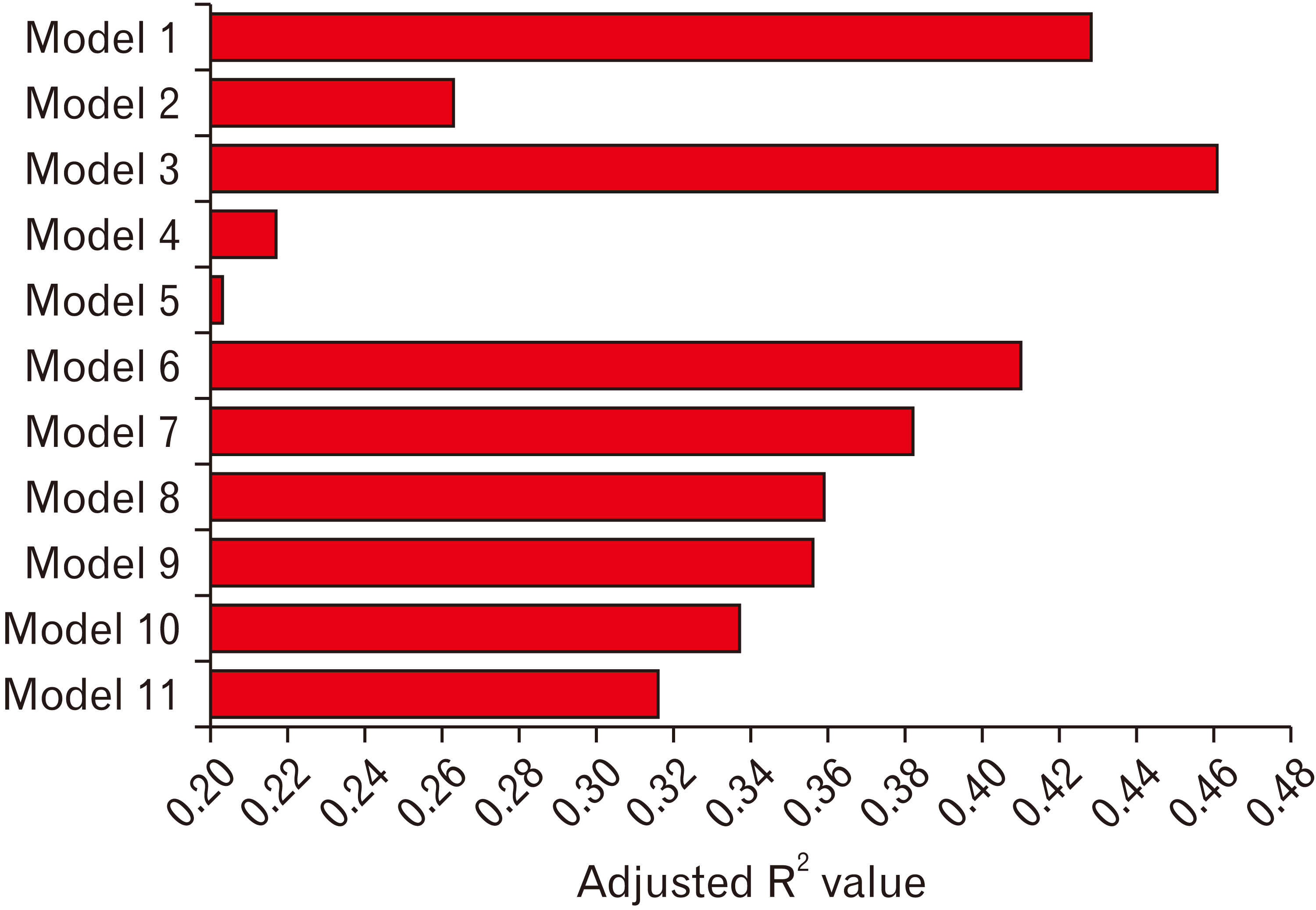 | Fig. 2Comparison of coefficient of determination (adjusted R2) values for each regression model. The x-axis represents adjusted R2 values, and the y-axis represents regression models based on various combinations of sextants. |
Table 6
| Tooth type | Pearson’s correlation coefficient | |||||
|---|---|---|---|---|---|---|
| V | X | T | F | P | L | |
| 11 | –0.4156* | 0.3126* | 0.0682 | –0.0124 | 0.3015* | 0.0815 |
| 12 | –0.4031* | 0.3148* | 0.0493 | 0.0298 | 0.2666* | 0.0924 |
| 13 | –0.4451* | 0.2428* | 0.1310* | 0.0510 | 0.3372* | 0.0932 |
| 14 | –0.3466* | 0.2158* | 0.1698* | –0.0065 | 0.2932* | 0.0965* |
| 15 | –0.4176* | 0.3664* | 0.0448 | –0.0279 | 0.2948* | 0.1477* |
| 16 | –0.3364* | 0.3809* | 0.0491 | –0.2219* | 0.2578* | 0.2121* |
| 17 | –0.3965* | 0.4551* | 0.0761 | –0.2349* | 0.2509* | 0.2048* |
| 21 | –0.3961* | 0.3412* | 0.0537 | –0.0472 | 0.2780* | 0.1231* |
| 22 | –0.4188* | 0.3009* | 0.0888 | 0.0526 | 0.2679* | 0.0819 |
| 23 | –0.4252* | 0.2446* | 0.1886* | 0.1038* | 0.3019* | 0.1368* |
| 24 | –0.3085* | 0.1532* | 0.1213* | –0.0434 | 0.3080* | 0.1430* |
| 25 | –0.4041* | 0.3763* | –0.0027 | –0.1216* | 0.2908* | 0.2228* |
| 26 | –0.3356* | 0.3940* | 0.0194 | –0.2451* | 0.2458* | 0.2231* |
| 27 | –0.4486* | 0.4461* | 0.1385* | –0.1858* | 0.2756* | 0.1676* |
| 31 | –0.4091* | 0.3379* | 0.1436* | 0.0816 | 0.3372* | N/A |
| 32 | –0.4113* | 0.2100* | 0.2440* | 0.0894 | 0.3393* | 0.0812 |
| 33 | –0.4388* | 0.1453* | 0.2473* | 0.1072* | 0.3545* | 0.1219* |
| 34 | –0.2717* | 0.0312 | 0.1922* | –0.0284 | 0.3319* | 0.0686 |
| 35 | –0.4119* | 0.2591* | 0.1579* | –0.1139* | 0.3661* | 0.2425* |
| 36 | –0.3201* | 0.3320* | 0.0039 | –0.2641* | 0.3069* | 0.2616* |
| 37 | –0.3992* | 0.3975* | 0.0111 | –0.2186* | 0.2463* | 0.2385* |
| 41 | –0.4461* | 0.3339* | 0.1747* | 0.0610 | 0.3504* | 0.0727 |
| 42 | –0.3928* | 0.2780* | 0.1707* | 0.0459 | 0.3236* | 0.0907 |
| 43 | –0.3982* | 0.2141* | 0.2453* | 0.0725 | 0.3114* | 0.0988* |
| 44 | –0.2922* | 0.0135 | 0.1763* | 0.0641 | 0.3143* | 0.1469* |
| 45 | –0.3769* | 0.2350* | 0.0909 | –0.0789 | 0.3217* | 0.2089* |
| 46 | –0.2889* | 0.2995* | 0.0492 | –0.2943* | 0.3274* | 0.2738* |
| 47 | –0.2999* | 0.3585* | 0.0906 | –0.3371* | 0.3543* | 0.2752* |
Table 7
This multiple linear regression was performed with the number of teeth observed for dental codes and chronological age. The estimated age can be calculated as the sum of the products of each number of teeth observed for a dental code and its respective coefficient plus its respective intercept. The definitions for each code are provided in Table 2. RMSE, root mean square error; adjusted R2, coefficient of determination.




 PDF
PDF Citation
Citation Print
Print



 XML Download
XML Download