This article has been
cited by other articles in ScienceCentral.
Abstract
Randomized controlled trials (RCTs) are considered the most rigorous study design for testing hypotheses and the gold standard for evaluating intervention effectiveness. However, RCTs are often conducted under the assumption of ideal conditions that may differ from real-world scenarios in which various issues, such as loss to follow-up, mistakes in participant enrollment or intervention, and low subject compliance or adherence, may occur. There are various group-defining strategies for analyzing RCT data, including the intention-to-treat (ITT), as-treated, and per-protocol (PP) approaches. The ITT principle involves analyzing all participants according to their initial group assignments, regardless of study completion and compliance or adherence to treatment protocols. This approach aims to replicate real-world clinical settings in which several anticipated or unexpected conditions may occur with regard to the study protocol. For the PP approach, only participants who meet the inclusion criteria, complete the interventions according to the study protocols, and have primary outcome data available are included. This approach aims to confirm treatment effects under optimal conditions. In general, the ITT principle is preferred for superiority and inequality trials, whereas the PP approach is preferred for equivalence and non-inferiority trials. However, both analytical approaches should be conducted and their results compared to determine whether significant differences exist. Overall, using both the ITT and PP approaches can provide a more complete picture of the treatment effects and ensure the reliability of the trial results.
Go to :

Keywords: Data analysis, Intention to treat analysis, Intervention study, Randomized controlled trial, Statistics, Treatment outcome
Gap between real and ideal
A randomized controlled trial (RCT) is an experimental research design in which researchers introduce one or more interventions and subsequently observe the outcomes [
1]. Scientifically rigorous methodologies such as randomization and blinding are typically applied in RCTs. Randomization ensures that each participant has an equal chance of being assigned to one or more interventions, eliminating the potential bias that may arise if researchers arbitrarily or intentionally assign participants to intervention groups [
2]. Blinding of participants, investigators, observers, data analysts, and/or others involved in the study to the assigned groups reduces or eliminates biases that may arise from deviations from the intended intervention and/or biases in the measurement of outcomes [
1]. Therefore, RCTs are considered the most scientifically rigorous study design for testing hypotheses and the gold standard for evaluating the effectiveness of interventions. RCTs are considered to provide a high level of evidence regarding the effectiveness of the interventions [
3].
RCTs are assumed to be conducted under ideal conditions, which may differ from real-world scenarios. In an ideal setting, all eligible participants are randomly assigned to the intervention groups, meet the eligibility and inclusion criteria, follow the trial protocols perfectly with no loss to follow-up, and have no missing data. In this ideal setting, which subjects need to be included in analysis is obvious. The trial design and implementation should strive to achieve this ideal scenario as much as possible. However, in practice various situations may arise, such as loss to follow-up, mistakes in enrollment or intervention, and low subject compliance (passive behavior) or adherence (more positive, proactive behavior). These situations, which RCT researchers frequently encounter, are collectively referred to as “non-compliance,” “non-adherence,” or missing data [
4].
Go to :

Bias caused by non-compliance or non-adherence to study protocols
In clinical studies, participants may not always comply with or adhere to study protocols. They may forget to attend interventions or take medications, intentionally or unintentionally undergo other interventions or medications, fail to achieve proper outcomes, or withdraw from the study. Occasionally, researchers may also inadvertently enroll patients who do not meet the eligibility and inclusion criteria for the study. Strategies for dealing with non-compliance, non-adherence, or missing data (i.e., whether to include, exclude, or impute them) can affect the study results. Given that researchers hold conflicting beliefs regarding these strategies, disagreements can often occur. Therefore, researchers must have a good understanding of group-defining strategies to effectively plan how to handle non-compliance, non-adherence, or missing data in advance.
There are various group-defining strategies for analyzing RCT data, including the intention-to-treat (ITT), as-treated (AT), and per-protocol (PP) approaches, which may lead to different results. For example, if a researcher or analyst wants to demonstrate a positive result for an intervention compared to a control in a clinical trial, they may choose an optimistic group-defining strategy. However, this can lead to the overestimation of treatment effects, false positives, and conflicts between researchers. Therefore, it is important to plan in advance the group-defining strategy that will be used and clearly state it in the study protocol. Any possible issues such as inappropriate enrollment, protocol violations, withdrawals, and missing values should also be defined and addressed in advance. Specifically, the definitions and statistical strategies for PP and AT should be addressed in detail. Selecting a group-defining strategy after data collection can introduce researcher and analyst bias.
Owing to the growing recognition of the importance of evidence-based medicine, the number of meta-analyses and network meta-analyses published that quantitatively synthesize the results of RCTs has increased [
5,
6]. In meta-analyses or network meta-analyses, the choice of group-defining strategies among ITT, AT, and PP can result in significantly different outcomes [
7]. Overall, careful planning and transparency are essential for the appropriate handling of non-compliance, non-adherence, or missing data in research studies.
Go to :

Study example
A virtual study example was designed to demonstrate the different group-defining strategies for analyzing RCT data (i.e., ITT, AT, and PP). This virtual study aims to compare the severity of postoperative sore throat in patients who undergo surgery under general anesthesia in the supine position within 2 h. Twelve patients were randomly assigned to two groups: six in the streamlined liner of the pharyngeal airway (SLIPA) group and six in the intubation group. Patients with diabetes, gastroesophageal reflux, neurological diseases, musculoskeletal diseases, or ankylosing spondylitis were excluded. The primary outcome was the severity of postoperative sore throat measured using the visual analog scale (VAS) at 2, 4, 12, 24, and 48 h postoperatively.
The ideal scenario would be for patients to complete the trials as soon as they are randomized and allocated. However, unexpected events can occur in real-world settings. For example, patients E and F in the SLIPA group received endotracheal intubation because of the difficulty in SLIPA insertion to complete the trials. Although this can occur at any time in the clinical setting, it complicates comparisons between the SLIPA and intubation groups (
Fig. 1A).
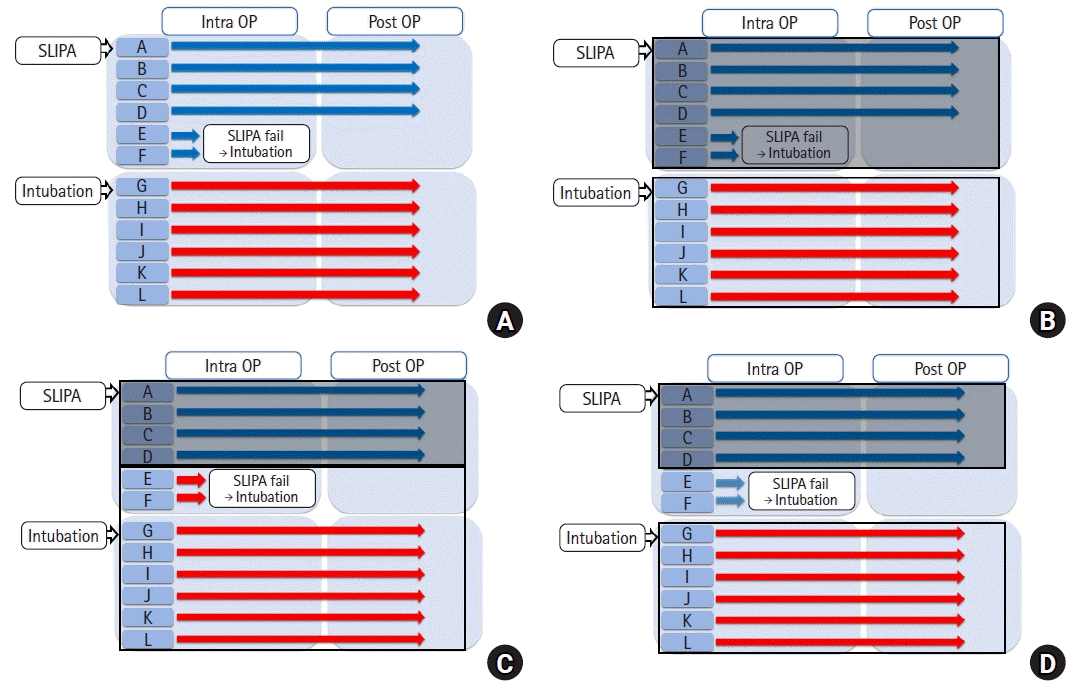 | Fig. 1.Virtual study example. (A) Study flow diagram, and (B) intention-to-treat, (C) as-treated, and (D) per-protocol approaches. Twelve patients were randomly assigned to the streamlined liner of pharyngeal airway (SLIPA) (n = 6) and intubation (n = 6) groups. Patients E and F in the SLIPA group received endotracheal intubation instead of SLIPA owing to difficulty with SLIPA insertion for completing the trials. The transparent rectangle refers to the subjects included in the intubation group, while the opaque rectangle represents the SLIPA group. (D) The faint arrow indicating patients E and F shows the subjects who were ultimately excluded from the study. 
|
Various group-defining strategies were used to compare the SLIPA and intubation groups. For group-defining strategy 1, the six patients (A, B, C, D, E, and F) randomized to the SLIPA group are compared to the six patients (G, H, I, J, K, and L) randomized to the intubation group (
Fig. 1B). For group-defining strategy 2, the four patients (A, B, C, and D) who underwent an SLIPA are compared with the eight patients (E, F, G, H, I, J, K, and L) who underwent intubation, regardless of group assignment (
Fig. 1C). For group-defining strategy 3, the four patients (A, B, C, and D) in the SLIPA group are compared to the six patients (G, H, I, J, K, and L) in the intubation group (
Fig. 1D).
For practical purposes, applying group-defining strategy 2, which compares patients who actually underwent an SLIPA insertion and intubation, is appropriate. However, let us assume that the two patients with failed SLIPA insertions had abnormal airway anatomies, which contributed to the sore throat postoperatively. As the patients were randomized into the groups, let us assume that the intubation group would have approximately two patients with abnormal anatomies. However, we do not know the identity of these patients. For simplicity, we refer to these patients as patients K and L.
For group-defining strategy 3, the patients (E and F) with abnormal airway anatomy were not included in the SLIPA group, while the intubation group included two patients (K and L) with abnormal anatomies (
Fig. 1D). This is not a fair comparison of the two groups as it introduces bias. For group-defining strategy 2, no patients with abnormal airway anatomies were included in the SLIPA group, while four patients (patients E, F, K, and L) with abnormal anatomies were included in the intubation group (
Fig. 1C), potentially introducing more bias than group-defining strategy 3.
Group-defining strategy 1 is the only approach that fairly compares the two groups, as it includes two participants with abnormal airway anatomies in each group (
Fig. 1B). Thus, the randomized nature of group-defining strategy 1 allows for a more unbiased comparison of postoperative pain between the two groups. Strictly speaking, however, group-defining strategy 1 is a comparison of the severity of postoperative sore throat after the SLIPA, or intubation if SLIPA is not possible, and intubation.
However, performing a clinical study is complex and challenges in clinical research and data analysis are often met, as shown in
Fig. 2A. For example, outcome data for patient D in the SLIPA group could not be obtained owing to loss to follow-up, and patients E and F in the SLIPA group received endotracheal intubation instead of SLIPA owing to difficulty with SLIPA insertion. In the intubation group, patient J expired during surgery, the researcher unintentionally inserted an SLIPA into patient K, and patient L was found to have a history of diabetes, and thus should have been excluded according to the exclusion criteria.
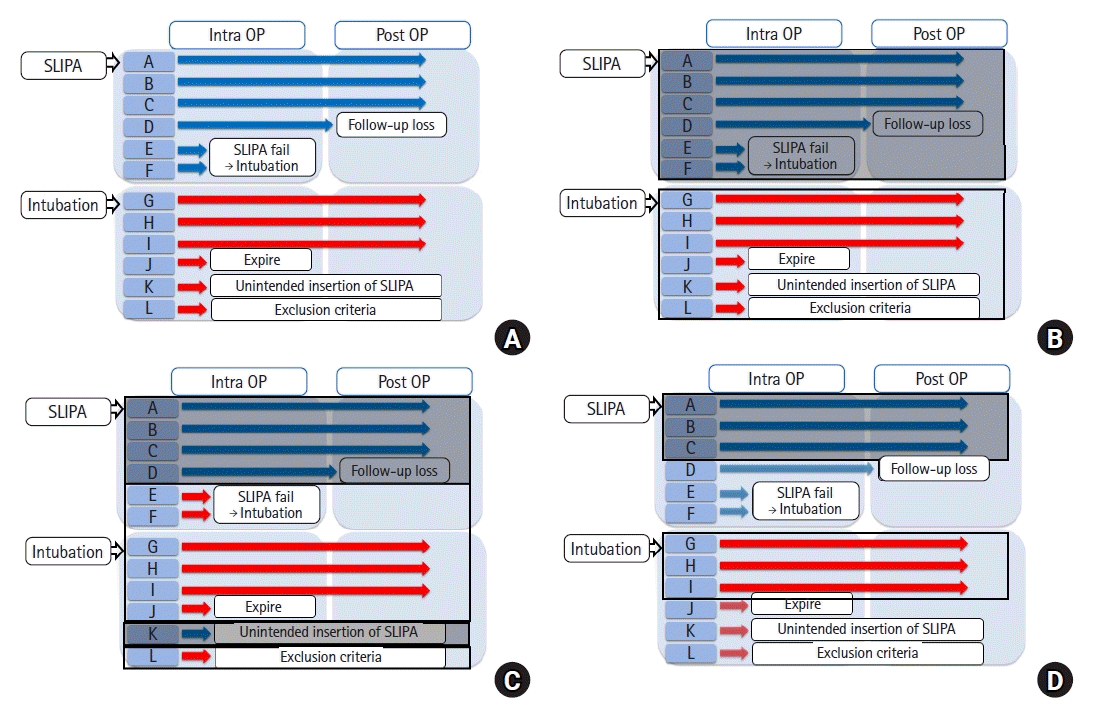 | Fig. 2.Complex study example. (A) Study flow diagram and (B) intention-to-treat, (C) as-treated, and (D) per-protocol approaches. Twelve patients were randomly assigned to the streamlined liner of pharyngeal airway (SLIPA) (n = 6) and intubation (n = 6) groups. Patient D was lost to follow up, and patients E and F in the SLIPA group received endotracheal intubation instead of SLIPA owing to difficulty with SLIPA insertion. Patient J expired during the surgery. The researcher unintentionally inserted an SLIPA into patient K, and patient L in the intubation group was found to have a history of diabetes and should have been excluded during enrollment. The transparent rectangle refers to the subjects included in the intubation group, while the opaque rectangle represents the SLIPA group. (D) The faint arrow indicating patients D, E, F, J, K, and L shows the subjects who were ultimately excluded from the study. 
|
Researchers also face several challenges during data analysis. First, they need to decide whether to include or exclude subjects who do not meet the inclusion criteria (e.g., patient L). Second, for the participants who received a different intervention than the randomized group they were assigned to, researchers must decide which group to include them in (e.g., patients E, F, and K). Third, they need to decide whether to exclude or include patients with missing data (e.g., patients D and J). Additionally, if they decide to include patients with missing data, they must decide how the data should be handled. In this study, we introduce various group-defining strategies (i.e., ITT, AT, and PP) in relation to this study example and explain how they can be used to address problems encountered.
Go to :

Intention to treat (ITT)
The ITT principle is a group-defining strategy in which patients are maintained in the initial intervention group to which they were randomized and assigned, regardless of whether they actually received that intervention. With this approach, biases that can occur if some patients are noncompliant or nonadherent to protocols or excluded from the analyses are avoided. According to the ITT principle, all patients should be included in the group to which they are initially assigned as much as possible to preserve the essence of randomization, even if they do not receive the intended treatment, meet the inclusion criteria, or follow the study protocols.
Figs. 1B and
2B describe the ITT principle. Using this strategy, patients who did not receive the assigned treatment (SLIPA) (i.e., patients E and F) remain in the groups to which they were initially assigned (
Figs. 1B and
2B). Similarly, patient K would be included in the intubation group, as initially assigned (
Fig. 2B). Additionally, patients who did not meet the inclusion criteria (i.e., patient L) would be included in the analysis. Finally, even though some data were missing for certain patients (i.e., patients D and J), they were included in the analyses (
Fig. 2B).
As such deviations from the study protocol can even occur in well-controlled clinical trials, they occur even more often in real-world scenarios. Therefore, it is more realistic to include patients with such deviations in the analyses (ITT principle). Thus, using the ITT principle, the analysis of study data is as unbiased as possible. The Cochrane Collaboration also strongly recommends using the ITT principle and reporting results in clinical trials [
8].
However, achieving the ITT principle in real-world settings is difficult. Therefore, a modified version of the ITT principle, called the modified ITT (mITT) principle, has been introduced. This approach allows for some deviations from the ideal ITT principle. For example, the mITT principle may only include patients who meet certain diagnostic criteria or receive standard treatments, or only those who have baseline assessments or are followed up for a certain length of time [
9]. However, the definition of the mITT used in clinical trials is often inconsistent and arbitrary.
The statistical principles for clinical trials (ICH E9) guideline introduces the term “full analysis set” (FAS), which is also a type of mITT. The FAS is as complete and as close as possible to the ITT ideal of including all randomized subjects. These guidelines allow for the exclusion of subjects who fail major entry criteria, such as no applied treatment and no data available after randomization [
10]. However, these major entry criteria are not commonly used to define the ITT principle [
11].
Go to :

As treated (AT)
The AT approach is a group-defining strategy in which patients are assigned to the analysis group according to the actual treatment received regardless of their randomization assignment [
4,
12]. This approach should be compared with the ITT principle, in which participants are analyzed according to their randomization assignments. In an ideal setting in which all participants receive their allocated treatments without errors, the results would be the same, though this is often not the case.
Figs. 1C and
2C show examples of the AT principle for participants who did not receive their randomly allocated treatments. In the study example, patients E and F were supposed to undergo an SLIPA insertion but underwent intubation instead (
Figs. 1C and
2C), while patient K was supposed to undergo intubation but underwent an SLIPA insertion instead (
Fig. 2C).
Using the ITT principle, participants who receive an intervention other than the randomly assigned intervention are analyzed according to their randomized assignments; thus, patients E and F were analyzed as part of the SLIPA group, and patient K was analyzed as part of the intubation group (
Figs. 1B and
2B). However, when using the AT approach, participants who receive an intervention other than the randomly assigned intervention are analyzed based on the actual treatments received. Hence, in this case, patients E and F were analyzed as part of the intubation group, and patient K was analyzed as part of the SLIPA group (
Figs. 1C and
2C).
Go to :

Per protocol (PP)
Unlike the ITT principle, which considers only the randomized groups without excluding any subjects, and the AT approach, which considers only the actual treatments received without excluding subjects for noncompliance, nonadherence, or with missing data, the PP approach aims to confirm treatment effects under optimal conditions [
13]. With the PP strategy, only subjects who meet the following criteria are included: 1) absence of major predefined protocol violations of the inclusion criteria, 2) completion of a pre-specified intervention, and 3) availability of data on the primary outcome [
14].
Some subjects can be excluded from the study if the PP strategy is used. For example, patients with major predefined protocol violations in the inclusion criteria (e.g., patient L), those who do not follow the randomly assigned interventions (patients E, F, and K) (
Figs. 1D and
2D), and those with missing data for the primary outcome (patients D and J) would be excluded (
Fig. 2D). Consequently, only three patients in the SLIPA group (patients A, B, and C) and three patients in the intubation group (patients G, H, and I) would be included (
Fig. 2D).
The PP approach is more likely to detect a difference between the experimental and control groups than the ITT principle because it only includes subjects who comply with or adhere to the study protocol without violations. This can lead to more significant differences between the groups. Researchers may be interested in detecting a treatment effect when compliance or adherence to the protocol is optimal, and the treatment effect based on the PP approach may be of greater interest to patients deciding whether to undergo a treatment.
The most critical aspect of using the PP approach is establishing clear subject inclusion or exclusion criteria during the study planning stage rather than during the analysis stage. If the study protocol is not accurately complied with or adhered to, the group that a subject belongs to may be ambiguous. Furthermore, specific reasons for excluding participants, such as the use of medications in the exclusion criteria, poor compliance or adherence, loss to follow-up, and missing data, should be predetermined. Additionally, researchers should carefully consider how excluding a subject for a specific reason may affect the study outcomes. This ensures that the analysis is unbiased and that any differences observed between the groups are attributable to the intervention itself rather than any methodological differences.
Go to :

ITT vs. PP
In clinical trials, the AT and PP approaches can be difficult to interpret because the benefits of randomization (elimination of systematic errors in treatment assignment) are lost and thereby bias is introduced into the results [
12]. This occurs when patients who adhere to their assigned treatments differ from those who do not adhere in ways that also affect outcomes. To address this issue, statistical techniques can be applied to account for potential variations among patients who do and do not adhere to their assigned treatments [
4].
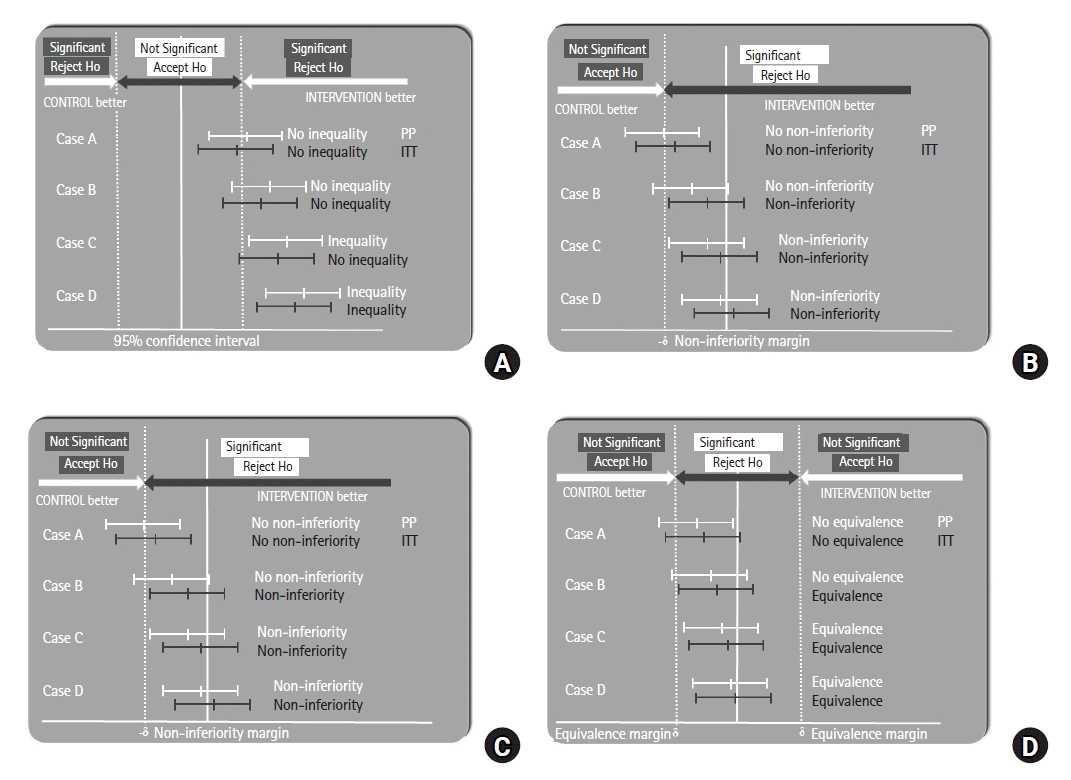
With the ITT principle, in which participants who do not receive their assigned interventions, are not compliant or adherent to protocols, or have missing data for the primary outcome are included, the estimated treatment effects may be diminished and diluted [
15], generally moving the intervention effect size toward zero (
Figs. 3A–
D). If adherence to a treatment is linked to a greater treatment effect, the treatment effect predicted by the ITT-based approach is frequently smaller than the effect size assessed using the PP-based approach [
16].
 | Fig. 3.Comparison of treatment effects between the intention-to-treat (ITT) and per-protocol (PP) approaches. (A) Inequality trial, (B) superiority trial, (C) non-inferiority trial, and (D) equivalence trial. The white line represents the ITT approach, and the gray line represents the PP approach. 
|
Thus, the ITT principle is often the preferred primary analysis approach because it is more conservative and less likely to uncover differences between groups in terms of superiority or inequality in RCTs (that seek to show investigational products as superior or unequal). In
Figs. 3A and
B, we see that in Case C, the null hypothesis can be rejected using the PP approach but not using the ITT approach. Therefore, a case that does not show a difference or superiority using the ITT approach will show a difference or superiority using PP.
However, in equivalence or non-inferiority trials (which seek to show equivalent or non-inferior treatment effects, respectively), diminishing and diluting the treatment effects of the ITT principle can result in the two treatment arms having similar outcomes [
17]. In
Figs. 3C and
D, we see that in Case B, the null hypothesis cannot be rejected using PP but can be rejected using the ITT principle. Therefore, cases that do not show equivalence or non-inferiority with PP may show equivalence or non-inferiority with the ITT principle. However, this increased possibility of rejecting the null hypothesis makes the ITT principle less conservative and can lead to inappropriate claims of equivalence or non-inferiority. In such cases, the PP may be more appropriate [
18].
Similarly, when performing comparisons with placebo or sham groups, the ITT principle is the preferred group-defining strategy for primary analysis in superiority trials, which is the most common design for interventional studies. However, in equivalence or non-inferiority trials comparing a treatment with a placebo or sham group or in superiority or inequality trials comparing a treatment to an active drug, the application of the ITT principle is generally not conservative. Therefore, whether to use ITT must be considered carefully [
19]. However, in most antibiotic non-inferiority trials, the ITT principle is more conservative than the PP approach [
20]. This may be attributable to the lower treatment success rate, which contributes to a higher variance and wider CI using the ITT principle than using the PP, thus resulting in a lower CI limit. Consequently, although the PP is frequently recommended as the primary group-defining strategy for studies examining non-inferiority, serious concerns about its potential for informative censoring have been voiced.
Therefore, it is important to conduct analyses based on both the ITT principle and PP and to document all subjects who are included in the trial or excluded from the analyses [
20]. The reasons for exclusion should be noted and the effects of all losses on the main analyses should be carefully considered. When both the ITT principle and the PP approach are used for analyzing the results of clinical trials and lead to similar conclusions, confidence in the trial results increases. Otherwise, efforts should be made to determine the cause of differences between the results. If the results from the PP approach demonstrate a more favorable treatment effect than those obtained using the ITT principle, this may suggest that participants adhering to and/or complying with the treatment had better results. A high dropout rate or missing data may dilute the treatment effect from the ITT principle because this approach incorporates all participants, even those with incomplete data. Substantial differences between the results obtained from the ITT principle and PP approach may imply difficulties in the generalizability of the treatment to real-world settings.
Therefore, the CONSORT guidelines also strongly suggest that estimates from both the ITT and PP approaches be provided in trial reports [
21]. However, excluding a significant proportion of subjects from the PP approach may raise questions about the overall validity of the trial.
Go to :

Missing data
Missing data can arise due to the attrition or exclusion of participants from the study. Attrition occurs when the participants are lost to follow-up, withdraw from the study, or fail to provide adequate data. Exclusion occurs when a participant does not meet the study inclusion criteria or is excluded for other reasons during the course of the study. Missing data can lead to various problems including a reduction in statistical power, bias in parameter estimation, reduced sample representativeness, and complications in study analysis. These distortions can threaten the validity of the trial and lead to invalid conclusions [
22].
Missing data is typically handled using statistical methods such as complete case analysis or list-wise deletion (i.e., ignoring, deleting, or analyzing data from incomplete subjects with missing data) or imputation (i.e., substituting some value for the missing data and performing analyses using the imputed value) or analyzing incomplete data using methods that do not require a complete dataset (i.e., likelihood-based methods, moment-based methods, and semi-parametric models for survival data). In addition, researchers can perform sensitivity analyses to evaluate the robustness of the results when applying various statistical methods or assumptions.
The choice of method depends on the primary group-defining strategy used for the primary outcome. For example, investigators may perform a complete case analysis with the PP approach or impute missing data for mITT analyses because with this approach, patients with missing data must be included.
Additionally, when researchers calculate sample sizes for their studies, they should consider the primary group-defining strategy. If they plan to use the ITT principle, their estimates of the effect size should be adjusted compared to the PP approach because the ITT principle includes data from non-compliant or non-adherent patients, those lost to follow-up, and those with missing data, which can reduce effect size estimates. The variability in adjusting the effect size estimate should also be considered. Additionally, when calculating sample sizes, researchers should consider dropout, non-compliance, or non-adherence rates, depending on whether the missing data will be included and/or imputed.
Go to :

Conclusion
There are various group-defining strategies for analyzing RCT data, including the ITT, AT, and PP approaches. The ITT principle aims to replicate real-world clinical settings, where many anticipated or unexpected events may occur that diverge from the study protocol. The PP approach, on the other hand, aims to confirm the treatment effects under optimal conditions.
In general, when comparing treatments to placebo or sham groups, the ITT principle is preferred for superiority or inequality trials, whereas the PP approach is preferred for equivalence or non-inferiority trials. However, analyses based on both the ITT principle and PP approach should be conducted, the results should be compared, and differences should be analyzed.
If research is conducted under ideal conditions without any non-compliance, non-adherence, or missing data, all datasets based on the ITT, AT, and PP approaches would be identical. However, deviations from ideal conditions in real-world settings are common. Hence, researchers should anticipate and account for these potential deviations during the planning stage and make decisions in advance regarding how to handle and incorporate such deviations into the resulting data. Overall, performing analyses using both the ITT principle and PP approach can provide a more complete picture of the treatment effects and help ensure the reliability of trial results.
Go to :







 PDF
PDF Citation
Citation Print
Print




 XML Download
XML Download