Aortic Annulus Detection Based on Deep Learning for Transcatheter Aortic Valve Replacement Using Cardiac Computed Tomography

Yongwon Cho; Soojung Park; Sung Ho Hwang; Minseok Ko; Do-Sun Lim; Cheol Woong Yu; Seong-Mi Park; Mi-Na Kim; Yu-Whan Oh; Guang Yang

doi:10.3346/jkms.2023.38.e306

Journal List > J Korean Med Sci > v.38(37) > 1516083868

Go to TopGo to Top Go to BottomGo to Bottom

TOOLS

Cho, Park, Hwang, Ko, Lim, Yu, Park, Kim, Oh, and Yang: Aortic Annulus Detection Based on Deep Learning for Transcatheter Aortic Valve Replacement Using Cardiac Computed Tomography

Original Article

Medical Imaging

Journal of Korean Medical Science 2023; 38(37): e306.

Published online: 4 September 2023

DOI: https://doi.org/10.3346/jkms.2023.38.e306

Aortic Annulus Detection Based on Deep Learning for Transcatheter Aortic Valve Replacement Using Cardiac Computed Tomography

Yongwon Cho^1,²

, Soojung Park¹

, Sung Ho Hwang¹

, Minseok Ko¹

, Do-Sun Lim³

, Cheol Woong Yu³

, Seong-Mi Park³

, Mi-Na Kim³

, Yu-Whan Oh¹

, Guang Yang^4,^5,^6,⁷

¹Department of Radiology, Korea University Anam Hospital, Seoul, Korea.

²AI Center, Korea University Anam Hospital, Seoul, Korea.

³Division of Cardiology, Department of Internal Medicine, Korea University Anam Hospital, Seoul, Korea.

⁴National Heart and Lung Institute, Imperial College London, London, United Kingdom.

⁵Cardiovascular Research Centre, Royal Brompton Hospital, London, United Kingdom.

⁶Bioengineering Department and Imperial-X, Imperial College London, London, United Kingdom.

⁷School of Biomedical Engineering & Imaging Sciences, King's College London, London, United Kingdom.

Address for Correspondence: Sung Ho Hwang, MD. Department of Radiology, Korea University Anam Hospital, 73 Goryeodae-ro, Seoungbuk-gu, Seoul 02841, Korea. sungho77@korea.ac.kr

Received 3 February 2023 Accepted 3 July 2023

The Korean Academy of Medical Sciences

https://creativecommons.org/licenses/by-nc/4.0/

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

Background

To propose a deep learning architecture for automatically detecting the complex structure of the aortic annulus plane using cardiac computed tomography (CT) for transcatheter aortic valve replacement (TAVR).

Methods

This study retrospectively reviewed consecutive patients who underwent TAVR between January 2017 and July 2020 at a tertiary medical center. Annulus Detection Permuted AdaIN network (ADPANet) based on a three-dimensional (3D) U-net architecture was developed to detect and localize the aortic annulus plane using cardiac CT. Patients (N = 72) who underwent TAVR between January 2017 and July 2020 at a tertiary medical center were enrolled. Ground truth using a limited dataset was delineated manually by three cardiac radiologists. Training, tuning, and testing sets (70:10:20) were used to build the deep learning model. The performance of ADPANet for detecting the aortic annulus plane was analyzed using the root mean square error (RMSE) and dice similarity coefficient (DSC).

Results

In this study, the total dataset consisted of 72 selected scans from patients who underwent TAVR. The RMSE and DSC values for the aortic annulus plane using ADPANet were 55.078 ± 35.794 and 0.496 ± 0.217, respectively.

Conclusion

Our deep learning framework was feasible to detect the 3D complex structure of the aortic annulus plane using cardiac CT for TAVR. The performance of our algorithms was higher than other convolutional neural networks.

Graphical Abstract

Keywords: Annulus Plane, Cardiac Image Analysis, Convolutional Neural Network, Deep Learning TAVR

INTRODUCTION

Aortic valve stenosis is a famous valvular heart disease in the world.1 Transcatheter aortic valve replacement (TAVR) should include analyzing a number of significant valve parameters before the surgical treatment. Palmer et al.2 developed algorithms to segment the aortic root. The main issues in reconstruction of aortic valve shape are visualization of valve function in real time and measurement of aortic root diameter in clinical settings. Another study aimed to reconstruct an aortic valve for patient-specific modeling using cardiac computed tomography (CT) images.3 Previously, methods for measuring valve annuli motion using cardiac magnetic resonance (MR) have utilized semi-automated feature tracking methods.4 Most cardiac MR tracking tools monitor the blood-myocardium boundary using maximum likelihood estimation.5

Deep learning6 is a subfield of machine learning inspired by artificial neural networks.7 Recently, an explosion of deep learning methods, such as convolutional neural networks (CNNs), multilayer perceptron, and recurrent neural network, has occurred with promise for predicting disease risks from medical datasets. Another study using deep learning8 robustly identified ten valve landmarks from orientations of three different long-axis MR images acquired in clinical setting. Recently, semantic segmentation using deep learning is important to infer meaningful parts with predefined annotations for each pixel in the medical datasets.9 10 11 Several studies have introduced segmentation algorithms based on CNNs combined with conditional random fields.12 Further, a fully convolutional network (FCN)13 and DeepLab14 have been introduced to improve the outputs of segmentation. Segmentation of three-dimensional (3D) volumetric medical images using 3D U-net has been successful.15 16 Cascade architectures which integrate segmentation and detection architectures and cascaded 3D FCN can perform more accurately using segmentation network combined with a region proposal network.18 19 20 21 22 23 Some researchers have developed methods based on CNNs to segment the atrium and ventricle in cardiac imaging.24 25 Astudillo et al.26 proposed CNNs architecture to automatically extract landmarks for preoperative TAVR.

In this study, we present our deep learning architecture to find 3D complex structures of the aortic annulus plane without finding specific landmarks for TAVR using cardiac CT and evaluate the performance of our algorithms (Annulus Detection Permuted AdaIN network [ADPANet]) by comparing with other CNNs (transformer-based 3D U-net, and original 3D U-net).

METHODS

This study retrospectively reviewed consecutive patients treated for aortic stenosis with TAVR using hospital information system records. The dataset consisted of selected scans from patients who underwent TAVR between January 2017 and July 2020. Total datasets were collected and preprocessed using cardiac CT. The model was trained using nnU-net,16 transformer-based U-net,27 and our model, including the permuted adaIN28 layer, root mean square error (RMSE) loss function, and a 3D U-net architecture, using a limited training dataset and ground truth were delineated manually by three radiologists. Our network is shown in Fig. 1. First, a radiologist found the main points noncoronary cusp (NCC), left coronary cusp (LCC), and right coronary cusp (RCC) to draw annuls plane about moving the CT scan view in AVIEW in Figs. 1 and 2.

Fig. 1

Overall, the deep learning architecture to automatically detect the aortic annulus.

ADPANet = Annulus Detection Permuted AdaIN network, NCC = noncoronary cusp, LCC = left coronary cusp, RCC = right coronary cusp, RCO = right cardiac output, LCO = left cardiac output.

Fig. 2

Examples of the gold standard for the annulus plane using cardiac computed tomography with AVIEW.

Datasets and pre-processing

The dataset consisted of 72 scans from patients who underwent TAVR between January 2017 and July 2020 (Table 1).

Table 1

Schematic representation of the study population

Characteristics		Training (n = 51)	Tuning (n = 10)	Test (n = 11)
Age, per patient		46 ± 14	38 ± 17.1	26 ± 6.3
Gender, per patient
	Male	32	4	3
	Female	19	6	7

Cardiac CTs were scanned using dual-layer spectral CT (IQon; Philips Healthcare, Best, The Netherlands). Intravenous contrast material (370 mg/mL iodine; Iopamiro; Bracco, Milan, Italy) was injected via an 18-gauge catheter placed in the antecubital vein. The protocol involved an initial injection (60–80 mL) of contrast medium at a rate of 5 mL/s, followed by 30 mL of saline at the same rate. CT was scanned in the cranio-caudal direction during an inspiratory breath-hold with retrospective electrocardiogram gating through tube current modulation. The bolus-tracking technique was triggered with a threshold of 100 Hounsfield units in the ascending aorta. The parameters for scanning were as follows: voltage, 120 kVp; current, 158–300 mAs; collimation, 64 × 0.625 mm; pitch, 0.16; gantry rotation time, 0.27 s; field of view, 257 mm; image matrix, 512 × 512; slice thickness, 0.9 mm; and slice increment, 0.45 mm. The CT dose-length product (in mGy · cm) was recorded for patients exposed to radiation during a CT scan. Effective dose (in mSV) was estimated by multiplying the dose-length product by the conversion factor (k = 0.017 mSv/mGy · cm) for the chest examination.

For the training, tuning, and test sets (about 80%:10%:10%) using a limited dataset, ground truth was delineated manually by three cardiac radiologists (S.H.H., and S.P. with 12, and 5 years of experience in cardiac imaging, respectively) with AVIEW platforms, version 1.1.40 (Coreline Software©, Seoul, Korea; https://www.corelinesoft.com) after manually finding NCC, LCC, and RCC using AVIEW.

The entailed labeling voxels on every cardiac CT slice included non-background (i.e., annulus plane) and background using the AVIEW software in Fig. 2.

All input datasets were resampled to 256 × 256 pixels (XY spatial size), including 120 slices along the Z direction, with the median voxel spacing of their corresponding dataset at the batch time. In total, 250 batches were used per epoch. We used third-order spline interpolation for cardiac CT and nearest-neighbor interpolation for the respective segmentation masks. Each cardiac CT image was normalized by the z-score method for intensity normalization. For efficient training, we performed aggressive data augmentation.

Architecture for training

We customized nnU-net based on 3D U-net16 to detect and localize the aortic annulus plane using cardiac CT in Fig. 3. The network includes an encoder and decoder parts. The left side diminished the dimensionality, whereas the right side expanded the original dimensionality. The encoder is similar to CNNs aggregating semantic features as spatial information is reduced. This network was customized in the encoder and decoder for more accurate semantic and spatial information to determine the aortic annulus plane. We added permuted AdaIN17 to the activation layers of the 3D convolution layers before batch normalization (BN).

(1)

p e r m u t e d A d a I N (p A d a I N) = \{\begin{matrix} x, p r o b a b i l i t y P \\ (p {I N}^{π} (x_{1}), ⃛, p {I N}^{π} (x_{N}) o t h e r w i s e \end{matrix}

Fig. 3

The architecture of ADPANet.

ADPANet = Annulus Detection Permuted AdaIN network.

where π is a uniformly selected permutation and p is a hyperparameter fixed ahead of training.

In addition, we first defined the BN operation:

(2)

µ_{c} (x) = \frac{1}{N} \sum_{n = 1}^{N} µ_{n c} (x)

(3)

σ_{c} = \sqrt{\frac{1}{N H W} \sum_{n = 1}^{N} \sum_{h = 1}^{H} \sum_{w = 1}^{W} {(x_{n c h w} - µ_{c} (x))}^{2} + ε}

(4)

B N (x) = γ (\frac{x - µ_{c} (x)}{σ_{c} (x)}) + β

for some parameters γ and β. After applying BN, we have:

(5)

µ_{n c} (B N (x)) = \frac{γ}{σ_{c} (x)} \cdot (µ_{n c} (x) - µ_{c} (x)) + β

(6)

σ_{n c} (B N (x)) = \frac{γ \cdot σ_{n c} (x)}{σ_{c} (x)}

With pAdaIN, when statistics are swapped (i.e., not identity):

(7)

µ_{n c} (B N (p A d a I N (x))) = \frac{γ}{σ_{c} (x)} \cdot (µ_{π (n) c} (x) - µ_{c} (x)) + β

(8)

σ_{n c} (B N (p A d a I N (x))) = \frac{γ \cdot σ_{π (n) c} (x)}{σ_{c} (x)}

Eq. 7 and Eq. 8 follow from pAdaIN shifting channel-wise statistics. After applying pAdaIN, the statistics of channel c for sample n are the same as those of the previous sample π(n). Hence, BN maintains to swap statistics and scales them using batch-wise statistics.

To expand the missing spatial information, U-net was used to perform this step as the decoder, which received semantic features from the low vertex of “U” and recombined all layers of the left part with those of the right part for skip connection. The two networks (encoder and decoder) consisted of convolution layers (or transposed) and upsampling or downsampling layers. A distinctive feature of 3D U-net was the concatenated architecture of encoder and decoder parts to improve segmentation. These features were achieved by integrating detailed anatomy from the down-sampling including the broader contextual features to the up-sampling path. In this study, each epoch consisted of 250 batches. In this network, leaky ReLU activation functions were replaced with random ReLUs, and loss functions were used, including dice coefficients, boundary loss functions, and binary cross-entropy (BCE). Adam optimization approach for stochastic gradient descent was used with an initial learning rate of 3 × 10⁻⁴ and a l2 weight decay of 3 × 10⁻⁵. The calculation of losses was conducted using the dice similarity coefficient (DSC), as shown in Eq. (9). The loss functions, dice loss (DL), and BCE are defined in Eq. (10) and Eq. (11), respectively. The volumes of the gold standard and inference for deep learning are defined by V_gs and V_seg, respectively.

(9)

D S C (V_{s e g}, V_{g s},) = \frac{2 | V_{s e g} \cap V_{g s} |}{|V_{s e g}| + |V_{g s}|},

(10)

D L = 1 - \frac{2 |V_{s e g} \cap V_{g s}|}{|V_{s e g}| + |V_{g s}|},

(11)

L (y, s) = −y log s − (1 − y) log (1 −s),

(12)

R M S E (P_{g}, P_{i}) = m e a n (\sqrt{\frac{j = \sum_{j = 1}^{n} {(P_{g, j} - P_{i, j})}^{2}}{n}})

where s and y denote the output probability and the corresponding gold standard, respectively.

In addition, the RMSE loss function (12) was used to measure the accuracy of the aortic annulus plane using cardiac CT.

where P_g is the pixel coordinate of the gold standard and P_i is the pixel coordinate of the inference.

Although we manually find NCC, LCC, and RCC using AVIEW, our network infers the presence and location of the aortic annulus plane in the multi-planar reconstruction view in Fig. 4 without any temporal consistency including three points. Therefore, images for time-series were not required.

Fig. 4

Aortic annulus plane in the multi-planar reconstruction view.

LCC = left coronary cusp, NCC = noncoronary cusp, RCC = right coronary cusp.

Experimental setups

To detect the aortic annulus of patients who underwent TAVR in CT, each axial section of volume was presented sequentially to the 3D CNN. The model was built in Python 3.8, using PyTorch. Training and testing were performed using PyTorch 3.8 and NVIDIA Titan RTX GPU (24 GB). For maximization of speed for training and optimization of the memory in GPU, larger input tiles and the batch size of four were applied. Adam optimizer was set with an initial learning rate of 3 × 10⁻⁴ and a l2-weight decay value of 3 × 10⁻⁵. The learning rate was decreased by a factor of 0.2 if the losses did not perform after 30 epochs. The optimal model was selected during training per epoch with the tuning datasets among the training datasets. We compared our algorithms (ADPANet including a Gaussian noise layer and pAdaIN) 3D U-net with others, including origin 3D U-net16 and transformer-based 3D U-net.26

Ethics statement

The Institutional Review Board for human investigations at the Korea University Anam Hospital (2020AN0355) approved the study protocol and the informed consent was waived due to the retrospective characteristic of this study. All datasets were de-identified to preserve privacy of patients. All processes were conducted in accordance with the relevant regulations and guidelines.

RESULTS

Performance evaluation for detection of aortic annulus plane

The total dataset consisted of 72 scans (Table 1). The proposed ADPANet and other CNNs were evaluated using clinical 3D cardiac CT. The accuracy of the aortic annulus plane was determined by obtaining DSC and RMSE, which are calculated by the distance between the gold standard labels and the inferences of the deep learning in Table 1. The DSC and RMSE achieved between the results of inference and gold standard were compared for 11 cases in Table 1. These were used in our and other algorithms (Table 2).

Table 2

Dice similarity coefficient and the root mean square error for detection of the aortic annulus plane using ADPANet, original 3D U-net, and transformer-based 3D U-net for test dataset (11 cases)

Measurements	ADPANet	Transformer-based 3D U-net	Original 3D U-net
RMSE	55.078 ± 35.794	58.862 ± 39.538	69.656 ± 65.230
DSC	0.496 ± 0.217	0.417 ± 0.261	0.495 ± 0.259

Data are shown as below: First (RMSE), p = 0.316 for ADPANet and transformer-based 3D U-net and p = 0.167 for ADPANet and original 3D U-net; Second (DSC), p = 0.711 for ADPANet and transformer-based 3D U-net and p = 0.172 for ADPANet and original 3D U-net.

ADPANet = Annulus Detection Permuted AdaIN network, 3D = three-dimensional, RMSE = root mean square error, DSC = dice similarity coefficient.

The outputs are presented in Figs. 5 and 6. In test dataset after training and tuning, (a), (b), and (c) show the areas of the aortic annulus plane in the axial, sagittal, and coronal view, and 3D volume rendering in cardiac CT, and (d) shows the aortic annulus plane. The green area is the gold standard by experts, and the red area is output of deep learning, including ADPANet, original 3D U-net, and transformer-based 3D U-net. The best cases among deep-learning algorithms were shown in Fig. 5. The worst cases among deep-learning algorithms were shown in Fig. 6.

Fig. 5

The best case among the detection of the aortic annulus plane. The top row is the output from ADPANet, the middle row is the output from transformer-based 3D U-net, and the bottom row is the output from original 3D U-net (green: gold standard, red: inference).

ADPANet = Annulus Detection Permuted AdaIN network, 3D = three-dimensional.

Fig. 6

The worst case among the detection of the aortic annulus plane. The top row is the output from ADPANet, the middle row is the output from transformer-based 3D U-net, and the bottom row is the output from original 3D Unet (green: gold standard, red: inference).

ADPANet = Annulus Detection Permuted AdaIN network, 3D = three-dimensional.

We also compared our algorithm with other algorithms in the literature. Table 2 lists the DSCs and RMSEs for detection of the aortic annulus plane using cardiac CT. The average RMSE values for the aortic annulus plane using cardiac CT with ADPANet, transformer-based 3D U-net, and original 3D U-net were 55.078 ± 35.794, 58.862 ± 39.538, and 69.656 ± 65.230, respectively. The average DSC values for the aortic annulus plane using cardiac CT with ADPANet, original 3D U-net, and transformer-based 3D U-net were 0.496 ± 0.217, 0.417 ± 0.261, and 0.495 ± 0.259, respectively.

DISCUSSION

Localization of the aortic annulus plane is important because of the variation of the aortic valve shape in the patients and the leaflet thickness, which is much smaller than two pixels in 3D cardiac CT with a resolution of 0.49 × 0.49 × 1.25 mm. Our study presents deep learning-based aortic annulus detection using 3D cardiac CT for automatically localizing and segmenting the aortic annulus plane. ADPANet is a customized nnU-net based on 3D U-net including permuted AdaIN. This is important to detect and localize the aortic annulus plane using cardiac CT. This layer helps to detect the aortic annulus plane around the critical areas, including shape and texture information from specific areas on CT.

Deep learning has been proposed for inferring complex structures and specific areas using a large volume of datasets.24 25 27 Meaningful segmentation outputs for the medical imaging have been obtained using 3D U-net.20 Other researchers have developed cascaded deep learning networks involving detection algorithms using multipath networks.18 19 Tang et al.22 proposed a cascaded architecture integrating segmentation and detection using the backbone of the VGG-16 network.20 Roth et al.21 also presented a cascading method with a second-stage FCN to detect and segment objects in target boundary regions. We customized 3D U-net to obtain robust and accurate results, including the RMSE loss and pAdaIN.

To evaluate the detection of the aortic annulus plane using ADPANET, the outputs of our algorithm were compared with those of others. The average RMSE value (56.078 ± 35.794) for detecting the aortic annulus plane using ADPANet outperformed that of transformer-based 3D U-net (58.862 ± 39.538) and original 3D U-net (69.656 ± 65.230). The average DSC value for ADPANet (0.496 ± 0.217) was higher than those reported by other CNNs (0.417 ± 0.261 and 0.495 ± 0.259). Using our algorithm, we localized the 3D aortic annulus plane, which is too complex to be detected using cardiac CT without any temporal consistency.

Previous studies28 29 30 31 32 33 34 35 have investigated structural and biomechanical interactions between the origin aortic root and a deployed transcatheter valve during TAVR. One limitation of these studies is that a 3D aortic valve model developed using 3D volume datasets often needs to be manually annotated by humans for experts. These methods are time-consuming for annotation, and prevent prompt collaboration with clinicians, to provide accurate model predictions.

Currently, various studies36 37 38 39 40 41 42 have demonstrated automatic segmentation and geometric reconstruction of specific areas for the shape of the four cardiac chambers, ventricular outflow tract, and aorta in cardiac medical images. For estimating valve shape, Zheng et al.43 have visualized 3D reconstructions of specific areas of the aorta using 3D C-arm CT. Pouch et al.44 have presented registration techniques to reconstruct the shape of aortic leaflet in 3D echocardiographic images with only three landmarks delineated by the clinician. Ionasec et al.45have developed methods for reconstructing mitral-aortic complex annotated (over 600 cases) from 3D volume for learning. These techniques require real-time reconstruction and visualization in the clinical field. In particular, analysis for TAVR requires a reconstructed aortic annulus plane or landmark point detection using cardiac CT. Otherwise, we didn’t directly compare our algorithms with previous studies36 37 38 39 40 41 42 because previous algorithms weren’t different from our methodology. However, there are several limitations in this study. We need to increase the number of datasets for training and tuning to improve accuracy.9 10 Next, our study excluded patients with aortic valve calcifications, which are prevalent in 18–53% of the general population aged > 50 years,46 47 48 49 accounting for approximately 82% of aortic stenosis.50 We aimed to decrease parameters such as calcium information to improve the performance of deep learning model in detection of the aortic annulus plane. Since we have verified the feasibility of the deep learning model in patients without aortic valve calcifications, we need to check whether the deep learning model can be trained well even when including patients with aortic valve calcifications. Finally, further validation using more datasets or multi-center datasets and comparison of performances with state-of-the-art network, is important to verify our algorithm detecting aortic annulus plane.

In conclusion, our deep learning architecture is feasible to detect the 3D complex structure of the aortic annulus using cardiac CT for TAVR comparing with other algorithms. It is expected that the time devoted to reconstructing the aortic annulus will be significantly reduced by applying the deep learning model to the clinical setting. More research is needed to verify the feasibility of deep learning in patients with aortic valve calcification and validate models in other medical centers.

ACKNOWLEDGMENTS

We would like to thank the Advanced Medical Imaging Institute in the Department of Radiology, Korea University Anam Hospital in the Republic of Korea, and the researchers for providing software, datasets, and various forms of technical support.

Notes

Funding: This research was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (2020R1I1A1A01071600) (2021K1A3A1A88101097) and (2021R1F1A1055272).

Disclosure: The authors have no potential conflicts of interest to disclose.

Author Contributions:

Conceptualization: Cho Y, Park S, Hwang SH.
Data curation: Ko M, Lim D, Yu CW, Park SM, Kim MN, Oh YW, Yang G, Hwang S.
Formal analysis: Cho Y.
Funding acquisition: Cho Y, Hwang SH.
Investigation: Cho Y, Park S, Hwang SH.
Methodology: Cho Y.
Writing - original draft: Cho Y, Park S, Hwang SH.
Writing - review & editing: Cho Y, Park S, Hwang SH.

References

1. Nkomo VT, Gardin JM, Skelton TN, Gottdiener JS, Scott CG, Enriquez-Sarano M. Burden of valvular heart diseases: a population-based study. Lancet. 2006; 368(9540):1005–1011. PMID: 16980116.

2. In : Palmer RI, Xie X, Tam GKL, editors. Automatic aortic root segmentation with shape constraints and mesh regularisation. Proceedings of the British Machine Vision Conference 2015; 2015 Sep 7-10; Swansea, UK. Durham: BMVA Press;2015.

3. Liang L, Kong F, Martin C, Pham T, Wang Q, Duncan J, et al. Machine learning-based 3-D geometry reconstruction and modeling of aortic valve deformation using 3-D computed tomography images. Int J Numer Method Biomed Eng. 2017; 33(5):e2827.

4. Leng S, Zhang S, Jiang M, Zhao X, Wu R, Allen J, et al. Imaging 4D morphology and dynamics of mitral annulus in humans using cardiac cine MR feature tracking. Sci Rep. 2018; 8(1):81. PMID: 29311562.

5. Schuster A, Hor KN, Kowallick JT, Beerbaum P, Kutty S. Cardiovascular magnetic resonance myocardial feature tracking: concepts and clinical applications. Circ Cardiovasc Imaging. 2016; 9(4):e004077. PMID: 27009468.

6. LeCun Y, Bengio Y, Hinton G. Deep learning. Nature. 2015; 521(7553):436–444. PMID: 26017442.

7. Schmidhuber J. Deep learning in neural networks: an overview. Neural Netw. 2015; 61:85–117. PMID: 25462637.

8. Kerfoot E, King CE, Ismail T, Nordsletten D, Miller R. Estimation of Cardiac Valve Annuli Motion With Deep Learning. Statistical Atlases and Computational Models of the Heart. M&Ms and EMIDEC Challenges. Updated 2021. Accessed January 29, 2021. http://www.who.int/whosis/en/menu.cfm .

9. In : Chen H, Qi X, Cheng JZ, Heng PA, editors. Deep contextual networks for neuronal structure segmentation. Proceedings of the AAAI Conference on Artificial Intelligence; 2016 Feb 12-17; Phoenix, AZ, USA. Washington, D.C: AAAI Press;2016.

10. Rao M, Stough J, Chi YY, Muller K, Tracton G, Pizer SM, et al. Comparison of human and automatic segmentations of kidneys from CT images. Int J Radiat Oncol Biol Phys. 2005; 61(3):954–960. PMID: 15708280.

11. In : Ronneberger O, Fischer P, Brox T, editors. U-net: convolutional networks for biomedical image segmentation. Medical Image Computing and Computer-Assisted Intervention -- MICCAI 2015: 18th International Conference; 2015 Oct 5-9; Munich, Germany. Cham, Switzerland: Springer International Publishing;2015.

12. In : Noh H, Hong S, Han B, editors. Learning deconvolution network for semantic segmentation. Proceedings of the IEEE International Conference on Computer Vision; 2015 Dec 7-13; Santiago, Chile. Manhattan: Institute of Electrical and Electronics Engineers (IEEE);2015. p. 1520–1528.

13. Shelhamer E, Long J, Darrell T. Fully convolutional networks for semantic segmentation. IEEE Trans Pattern Anal Mach Intell. 2017; 39(4):640–651. PMID: 27244717.

14. Chen LC, Papandreou G, Kokkinos I, Murphy K, Yuille AL. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected CRFs. IEEE Trans Pattern Anal Mach Intell. 2018; 40(4):834–848. PMID: 28463186.

15. In : Çiçek Ö, Abdulkadir A, Lienkamp SS, Brox T, Ronneberger O, editors. 3D U-net: learning dense volumetric segmentation from sparse annotation. Medical Image Computing and Computer-Assisted Intervention -- MICCAI 2016: 19th International Conference International Conference; 2016 Oct 17-21; Athens, Greece. Cham, Switzerland: Springer International Publishing;2016. p. 424–432.

16. Isensee F, Petersen J, Kohl SA, Jäger PF, Maier-Hein KH. nnU-Net: a self-configuring method for deep learning-based biomedical image segmentation. Nat Methods. 2021; 18(2):203–211. PMID: 33288961.

17. Nuriel O, Benaim S, Wolf L. Permuted AdaIN: Reducing the Bias Towards Global Statistics in Image Classification, IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). 2021.

18. Christ PF, Elshaer ME, Ettlinger F, Tatavarty S, Bickel M, Bilic P, et al. Automatic liver and lesion segmentation in CT using cascaded fully convolutional neural networks and 3D conditional random fields. In : Medical Image Computing and Computer-Assisted Intervention -- MICCAI 2016: 19th International Conference International Conference; 2016 Oct 17-21; Athens, Greece. Cham, Switzerland: Springer International Publishing;2016. p. 415–423.

19. Cui S, Mao L, Jiang J, Liu C, Xiong S. Automatic semantic segmentation of brain gliomas from MRI images using a deep cascaded neural network. J Healthc Eng. 2018; 2018:4940593. PMID: 29755716.

20. He Y, Carass A, Yun Y, Zhao C, Jedynak BM, Solomon SD, et al. Towards topological correct segmentation of macular OCT from cascaded FCNs. Fetal Infant Ophthalmic Med Image Anal. 2017; 10554:202–209.

21. Roth HR, Oda H, Zhou X, Shimizu N, Yang Y, Hayashi Y, et al. An application of cascaded 3D fully convolutional networks for medical image segmentation. Comput Med Imaging Graph. 2018; 66:90–99. PMID: 29573583.

22. In : Tang M, Zhang Z, Cobzas D, Jagersand M, Jaremko JL, editors. Segmentation-by-detection: a cascade network for volumetric medical image segmentation. 2018 IEEE 15th International Symposium on Biomedical Imaging; 2018 Apr 4-7; Washington, D.C., USA. Manhattan: IEEE Publications;2018. p. 1356–1359.

23. Wang G, Li W, Zuluaga MA, Pratt R, Patel PA, Aertsen M, et al. Interactive medical image segmentation using deep learning with image-specific fine tuning. IEEE Trans Med Imaging. 2018; 37(7):1562–1573. PMID: 29969407.

24. Penso M, Moccia S, Scafuri S, Muscogiuri G, Pontone G, Pepi M, et al. Automated left and right ventricular chamber segmentation in cardiac magnetic resonance images using dense fully convolutional neural network. Comput Methods Programs Biomed. 2021; 204:106059. PMID: 33812305.

25. Zhang X, Noga M, Martin DG, Punithakumar K. Fully automated left atrium segmentation from anatomical cine long-axis MRI sequences using deep convolutional neural network with unscented Kalman filter. Med Image Anal. 2021; 68:101916. PMID: 33285484.

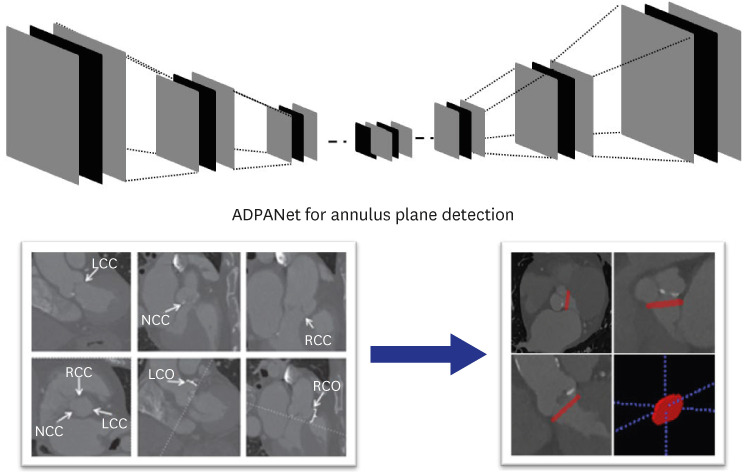
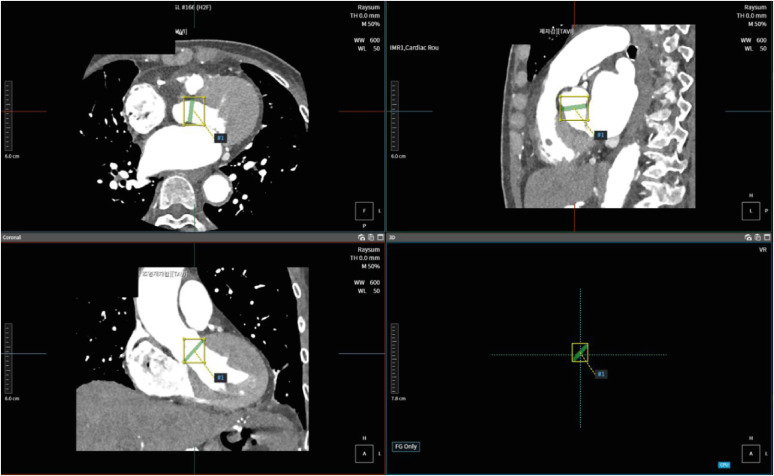
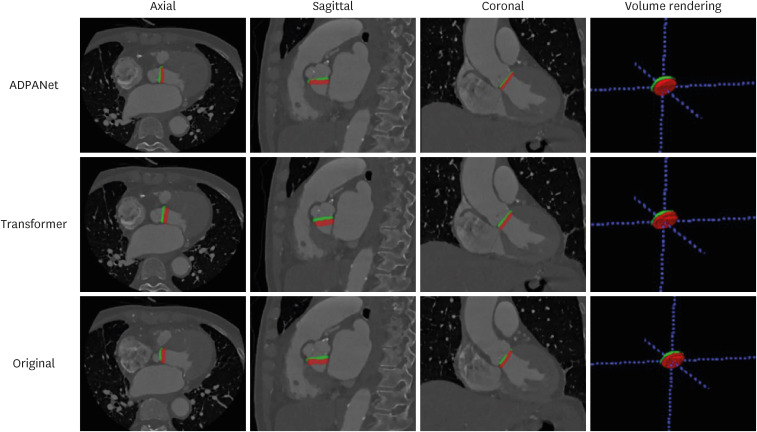
26. Astudillo P, Mortier P, Bosmans J, De Backer O, de Jaegere P, Iannaccone F, et al. Automatic detection of the aortic annular plane and coronary ostia from multidetector computed tomography. J Interv Cardiol. 2020; 2020:9843275. PMID: 32549802.

27. In : Xie Y, Zhang J, Shen C, Xia Y, editors. CoTr: efficiently bridging CNN and transformer for 3D medical image segmentation. Medical Image Computing and Computer-Assisted Intervention -- MICCAI 2021: 24th International Conference; 2021 Sep 27-Oct 1; Strasbourg, France. Cham, Switzerland: Springer International Publishing;2021. p. 171–180.

28. Auricchio F, Conti M, Morganti S, Reali A. Simulation of transcatheter aortic valve implantation: a patient-specific finite element approach. Comput Methods Biomech Biomed Engin. 2014; 17(12):1347–1357. PMID: 23402555.

29. Capelli C, Bosi GM, Cerri E, Nordmeyer J, Odenwald T, Bonhoeffer P, et al. Patient-specific simulations of transcatheter aortic valve stent implantation. Med Biol Eng Comput. 2012; 50(2):183–192. PMID: 22286953.

30. Dwyer HA, Matthews PB, Azadani A, Ge L, Guy TS, Tseng EE. Migration forces of transcatheter aortic valves in patients with noncalcific aortic insufficiency. J Thorac Cardiovasc Surg. 2009; 138(5):1227–1233. PMID: 19748632.

31. Morganti S, Conti M, Aiello M, Valentini A, Mazzola A, Reali A, et al. Simulation of transcatheter aortic valve implantation through patient-specific finite element analysis: two clinical cases. J Biomech. 2014; 47(11):2547–2555. PMID: 24998989.

32. Wang Q, Kodali S, Primiano C, Sun W. Simulations of transcatheter aortic valve implantation: implications for aortic root rupture. Biomech Model Mechanobiol. 2015; 14(1):29–38. PMID: 24736808.

33. Wang Q, Sirois E, Sun W. Patient-specific modeling of biomechanical interaction in transcatheter aortic valve deployment. J Biomech. 2012; 45(11):1965–1971. PMID: 22698832.

34. Morgan TG, Bostrom MP, van der Meulen MC. Tissue-level remodeling simulations of cancellous bone capture effects of in vivo loading in a rabbit model. J Biomech. 2015; 48(5):875–882. PMID: 25579991.

35. de Jaegere P, De Santis G, Rodriguez-Olivares R, Bosmans J, Bruining N, Dezutter T, et al. Patient-specific computer modeling to predict aortic regurgitation after transcatheter aortic valve replacement. JACC Cardiovasc Interv. 2016; 9(5):508–512. PMID: 26965945.

36. Huang X, Dione DP, Compas CB, Papademetris X, Lin BA, Bregasi A, et al. Contour tracking in echocardiographic sequences via sparse representation and dictionary learning. Med Image Anal. 2014; 18(2):253–271. PMID: 24292554.

37. Zhu Y, Papademetris X, Sinusas AJ, Duncan JS. Segmentation of the left ventricle from cardiac MR images using a subject-specific dynamical model. IEEE Trans Med Imaging. 2010; 29(3):669–687. PMID: 19789107.

38. Ecabert O, Peters J, Weese J. Modeling Shape Variability for Full Heart Segmentation in Cardiac Computed-Tomography Images. Bellingham, WA, USA: SPIE;2006.

39. Zheng Y, Barbu A, Georgescu B, Scheuering M, Comaniciu D. Four-chamber heart modeling and automatic segmentation for 3-D cardiac CT volumes using marginal space learning and steerable features. IEEE Trans Med Imaging. 2008; 27(11):1668–1681. PMID: 18955181.

40. Lorenz C, von Berg J. A comprehensive shape model of the heart. Med Image Anal. 2006; 10(4):657–670. PMID: 16709463.

41. In : Lin N, Papademetris X, Sinusas AJ, Duncan JS, editors. Analysis of left ventricular motion using a general robust point matching algorithm. Medical Image Computing and Computer-Assisted Intervention -- MICCAI 2003: 6th International Conference; 2003 Nov 15-18; Montréal, Canada. Berlin: Springer International Publishing;2003. p. 556–563.

42. Schneider RJ, Perrin DP, Vasilyev NV, Marx GR, del Nido PJ, Howe RD. Mitral annulus segmentation from four-dimensional ultrasound using a valve state predictor and constrained optical flow. Med Image Anal. 2012; 16(2):497–504. PMID: 22200622.

43. Zheng Y, John M, Liao R, Nöttling A, Boese J, Kempfert J, et al. Automatic aorta segmentation and valve landmark detection in C-arm CT for transcatheter aortic valve implantation. IEEE Trans Med Imaging. 2012; 31(12):2307–2321. PMID: 22955891.

44. Pouch AM, Wang H, Takabe M, Jackson BM, Sehgal CM, Gorman JH 3rd, et al. Automated segmentation and geometrical modeling of the tricuspid aortic valve in 3D echocardiographic images. Med Image Comput Comput Assist Interv. 2013; 16(Pt 1):485–492.

45. Ionasec RI, Voigt I, Georgescu B, Wang Y, Houle H, Vega-Higuera F, et al. Patient-specific modeling and quantification of the aortic and mitral valves from 4-D cardiac CT and TEE. IEEE Trans Med Imaging. 2010; 29(9):1636–1651. PMID: 20442044.

46. Aronow WS, Schwartz KS, Koenigsberg M. Correlation of serum lipids, calcium, and phosphorus, diabetes mellitus and history of systemic hypertension with presence or absence of calcified or thickened aortic cusps or root in elderly patients. Am J Cardiol. 1987; 59(9):998–999. PMID: 3565291.

47. Lindroos M, Kupari M, Heikkilä J, Tilvis R. Prevalence of aortic valve abnormalities in the elderly: an echocardiographic study of a random population sample. J Am Coll Cardiol. 1993; 21(5):1220–1225. PMID: 8459080.

48. Stewart BF, Siscovick D, Lind BK, Gardin JM, Gottdiener JS, Smith VE, et al. Clinical factors associated with calcific aortic valve disease. Cardiovascular Health Study. J Am Coll Cardiol. 1997; 29(3):630–634. PMID: 9060903.

49. Agmon Y, Khandheria BK, Meissner I, Sicks JR, O’Fallon WM, Wiebers DO, et al. Aortic valve sclerosis and aortic atherosclerosis: different manifestations of the same disease? Insights from a population-based study. J Am Coll Cardiol. 2001; 38(3):827–834. PMID: 11527641.

50. Ferreira-González I, Pinar-Sopena J, Ribera A, Marsal JR, Cascant P, González-Alujas T, et al. Prevalence of calcific aortic valve disease in the elderly and associated risk factors: a population-based study in a Mediterranean area. Eur J Prev Cardiol. 2013; 20(6):1022–1030. PMID: 22679252.

TOOLS

Similar articles