Abstract
Objectives
Intraoperative navigation reduces the risk of major complications and increases the likelihood of optimal surgical outcomes. This paper presents an augmented reality (AR)-based simulation technique for ventriculostomy that visualizes brain deformations caused by the movements of a surgical instrument in a three-dimensional brain model. This is achieved by utilizing a position-based dynamics (PBD) physical deformation method on a preoperative brain image.
Methods
An infrared camera-based AR surgical environment aligns the real-world space with a virtual space and tracks the surgical instruments. For a realistic representation and reduced simulation computation load, a hybrid geometric model is employed, which combines a high-resolution mesh model and a multiresolution tetrahedron model. Collision handling is executed when a collision between the brain and surgical instrument is detected. Constraints are used to preserve the properties of the soft body and ensure stable deformation.
Results
The experiment was conducted once in a phantom environment and once in an actual surgical environment. The tasks of inserting the surgical instrument into the ventricle using only the navigation information presented through the smart glasses and verifying the drainage of cerebrospinal fluid were evaluated. These tasks were successfully completed, as indicated by the drainage, and the deformation simulation speed averaged 18.78 fps.
Technologies from the Fourth Industrial Revolution, such as augmented reality (AR) and virtual reality, have been applied to various fields, with studies focusing on high value-added products. AR technology is becoming increasingly popular due to its ability to merge real-world perceptions with virtual images, providing an enhanced interactive experience and immersion [1]. These benefits also apply to the medical field, with AR being utilized in various areas such as surgical planning [2], virtual endoscopy [3], surgical training simulators [4], and AR surgical navigation systems [5]. Numerous studies have also employed AR in brain surgery [6–8].
Cabrilo et al. [6] used AR for arteriovenous malformation surgery. In their study, they augmented the segmented blood vessel information, obtained through three-dimensional (3D) digital subtraction angiography, onto the microscope lens. This enabled the surgeon to perform the surgery without needing to view a separate screen. Besharati Tabrizi et al. [7] were able to review magnetic resonance imaging (MRI), tumor boundaries, and other relevant information before performing a craniotomy by projecting the segmented lesion data onto the patient using a video projector. Watanabe et al. [8] visualized anatomical structures on images captured with a tablet PC. The tablet’s position was tracked using six cameras, and the intracranial structure was displayed at corresponding angles when viewed from different tablet directions.
The studies mentioned above employed AR to identify the location of anatomical structures in the brain. However, they did not take into account brain deformation, which can occur during surgery, and only overlaid the anatomical structures. Brain deformation takes place during surgery due to factors such as the patient’s posture, gravity, and manipulation by surgical instruments [9]. In ventriculostomy, the surgical instrument insertion path is planned using preoperative computed tomography (CT) or MRI, and the instrument is inserted along this path [10,11]. Consequently, discrepancies between the preoperative plan, which does not account for deformation, and the actual surgical situation, where anatomical deformation may occur, can impact the accuracy of the insertion route [12].
Several studies have taken brain deformation into account while investigating surgical procedures, but without AR [9,13]. In most of these studies, physical deformation models were implemented using the finite element method (FEM). Fukuhara et al. [14] created a simulator for opening the Sylvian fissure in the brain, allowing the operator to simulate the process while experiencing the reaction force from the deformed brain. During that simulation, brain deformation was modeled using FEM. Forte et al. [15] also employed FEM to simulate the brain shift phenomenon caused by cerebrospinal fluid loss during surgery. Although FEM can produce highly accurate simulations, its application during surgery is challenging due to the extensive computational requirements.
In contrast, position-based dynamics (PBD) [16] offers a physical deformation method comparable to FEM, representing brain deformation through a mass-spring system. This approach is characterized by its ability to perform rapid and robust calculations. Furthermore, simulation stability is ensured by employing an implicit method for interpretation. Flexibility errors, such as penetration phenomena, are addressed by directly controlling the mesh vertex position. Multiple studies have integrated PBD into soft-body deformation simulations. For instance, Pan et al. [17] converted 3D objects into spherical units and utilized PBD for constraint analysis between these spheres. Pan et al. [18] also reconstructed the spheres associated with the cutting plane to create a more natural soft-body cutting simulation. Romeo et al. [19] applied PBD to simulate skeletal muscle and fascia, conducting the simulation by defining a muscle fiber constraint that reflects changes caused by muscle contraction and fascia, and by assigning different strengths to each region.
This paper proposes an AR-based simulation technique for brain ventriculostomy that visualizes a 3D model of brain deformation caused by the movement of surgical instruments using a PBD physical deformation method.
The mesh and tetrahedron models are combined into a hybrid model following the semi-automatic segmentation of the preoperative brain image. Subsequently, an AR surgical environment is created to align the real world with the virtual space by registering trackable objects (e.g., smart glasses and surgical instruments) and utilizing infrared cameras. During surgery, the position of the surgical instrument is monitored in real time, and collision handling is implemented when a collision between the brain and the instrument is detected. At this stage, various constraints are applied to enable deformation that takes into account the heterogeneous nature and properties of soft bodies, such as brain tissue and ventricles. The soft-body deformation process is carried out iteratively based on units of time, facilitating the expression of natural soft-body movement (Figure 1).
The generation of each model used in AR ventriculostomy (skin, brain, and ventricle models) begins with the segmentation of the respective areas in the preoperative CT images. The skin area, where the background is removed from the preoperative image, represents the patient’s body surface and serves as the reference point for correlating the real world with the virtual space. The brain area consists of the target location for surgical instrument insertion and the simulation of deformation due to the movement of the surgical instrument. Each area is semi-automatically segmented using the livewire method [20], and a high-resolution 3D mesh model is created from each segmented area using a marching cube algorithm [21]. A continuum-based model is necessary to implement a sophisticated physical model, as the 3D mesh model only contains surface information, and the overall characteristics of the soft tissue must be considered. Therefore, the 3D mesh model is simplified using SOFA [22], and a tetrahedron model, in which each element consists of tetrahedron units, is generated. The method of Kim et al. [23], which generates a multiresolution tetrahedron model with tetrahedrons of varying sizes based on density, is employed for computational efficiency.
High-speed calculations are necessary due to the continuous brain deformation caused by surgical instruments. To address this, a hybrid geometric model, which combines a high-resolution mesh model and a multiresolution tetrahedron model, is utilized. This model offers a realistic representation while reducing the computational load of the simulation. A barycentric coordinate is employed for coordinate mapping between the adjacent vertices of the two models, allowing the deformation information of the tetrahedron model to be reflected in the high-resolution mesh model [24]. The PBD physical deformation modeling accounts for deformation information in the tetrahedron model when deformation occurs due to surgical instruments. Each vertex of the high-resolution mesh model is interpolated to the vertex position of the connected tetrahedron.
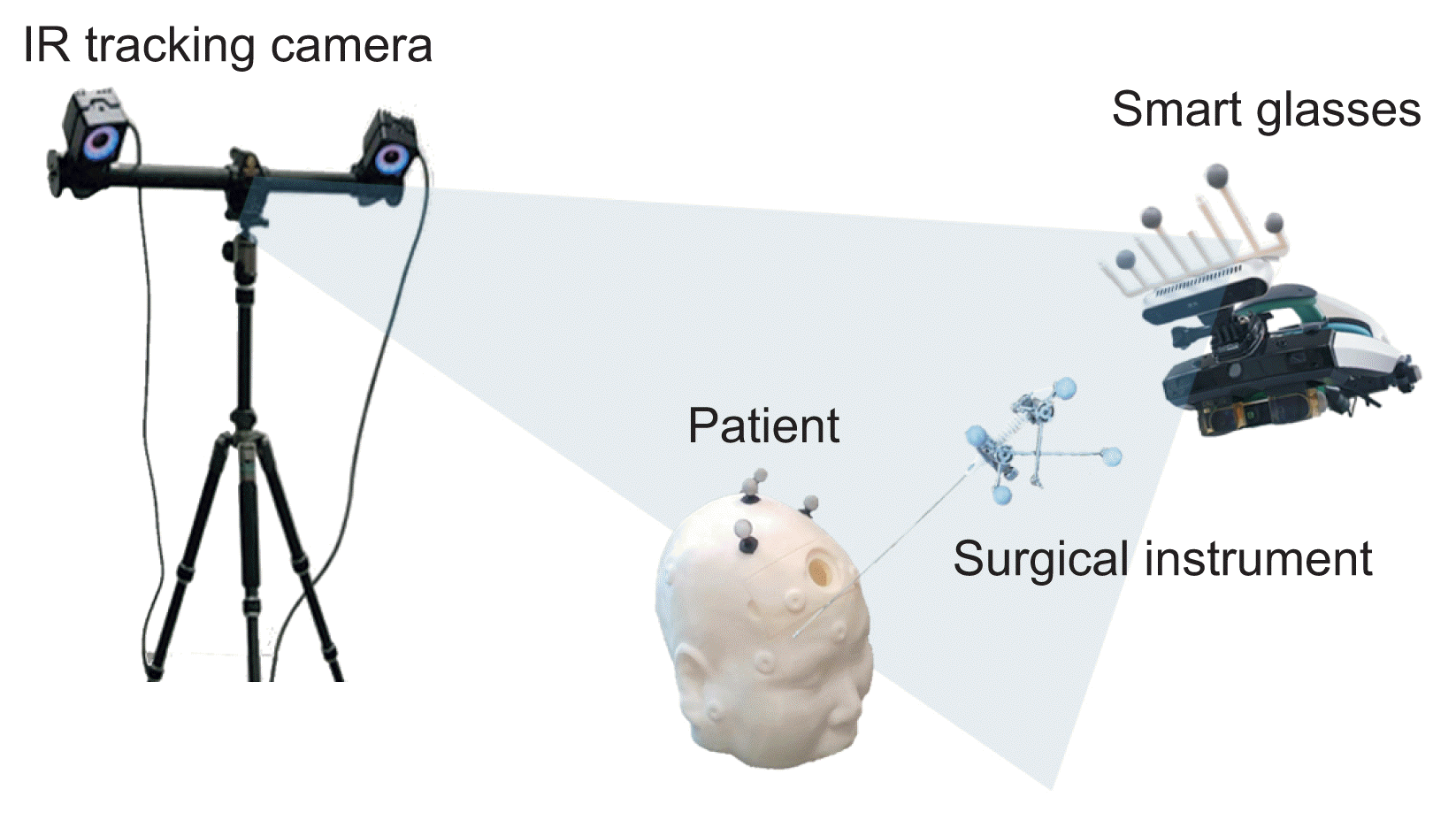
In this study, two infrared cameras (OptiTrack Prime 13) are utilized to locate the patient, smart glasses, and surgical instruments, while augmented 3D models displayed on the smart glasses provide navigational information to the clinicians. As a prerequisite, a virtual space must be modeled, and an AR surgical environment that aligns with both the virtual space and the real world should be established (Figure 2).
The virtual space is created using the Motive software [25]. The surgical area is sampled with a calibration tool that has attached infrared markers; the origin and axis are established using an alignment tool to construct the virtual space. Infrared markers affixed to the smart glasses and surgical instruments are reconstructed into rigid models within the virtual space, enabling the objects to be identified and tracked.
A calibration process for smart glasses is conducted to display a 3D model within a virtual space. The 3D coordinates of the checkerboard intersection, as indicated by the two-dimensional camera image and the checkerboard itself, are acquired with the assistance of infrared markers [26]. The camera parameter is derived from the linear relationship between the 3D coordinate and the two-dimensional coordinates on the image screen, utilizing the direct linear transform algorithm. Ultimately, the object within the virtual space is transformed into the smart glasses’ coordinate system and rendered [26].
Finally, it is necessary to align the 3D model with the patient in a supine position for surgery. In the affected area, a visually discernible feature that can also be characterized in the 3D model is designated as the matching feature point. The 3D coordinates of these corresponding feature points are acquired using a surgical instrument equipped with infrared markers. The feature points are then matched using the iterative closest point algorithm to establish a correlation between the real world and the virtual space [26] (Figure 3).
The PBD physical model is iterated to simulate soft-body deformation, taking into account external forces such as collision and gravity, as well as internal forces like elastic forces within the soft body. The geometric structure of the 3D deformation object, suitable for representing a soft body, is characterized by a vertex (p1…pn) possessing a mass of (wi = 1/mi). The deformation of the object is depicted as the displacement of the vertices obtained using:
Equation (1) represents the new speed (
) that corresponds to the external force (f) acting on the 3D soft-body model, internal damping, and mass at the current speed (vi) of the vertex; this equation is used to calculate the soft-body deformation caused by external forces. Equation (2) represents the (
) new vertex location resulting from the external forces, and it is estimated from the current location (pi) of the vertex and the velocity information (
) with respect to unit time (Δt) [16].
To obtain the deformation of a realistic 3D soft-body model, the estimated location information must be modified to an optimized location by applying a constraint that captures the soft tissue’s deformation characteristics. The Gauss-Seidel iteration technique was employed to analyze the constraint, minimizing unit time to naturally represent the deformation simulation. Moreover, the calculations for each constraint were repeated to converge the vertices to an optimal position [16]. A normalized coefficient was also utilized to adjust the strength of the constraints. The new vertex’s location (
) with the applied constraint represents a modified 3D soft-body model; the new velocity of the vertex is implicitly derived from the current location (
) and previous location (pi), as shown in Equation (5), before the next deformation [16].
The following constraint was applied to the physical deformation model to achieve stable deformation while maintaining the integrity of the soft body.
As shown in Equation (6), the stretch constraint is implemented using the difference between the initial distance (linit) and the current distance (|p1 – p2|) between the two vertices (p1, p2) to express the spring form, which is a basic element of the physical model [16]. In this scenario, rapid deformation is facilitated by approximating the variation of the projected distance of the edge connecting the vertices.
For a stable representation of bending motion in a model comprised of tetrahedrons, we apply equations that preserve both the internal angle of each tetrahedron and the angle between adjacent tetrahedrons. These equations are represented as follows [16,27]:
Assuming that the initial volume of the 3D soft-body object is conserved after deformation, any volume loss can be compensated for by considering the volume change based on the initial volume (V0) and the actual volume (V) using a previously described method [16].
To represent the heterogeneous nature of the brain and ventricle, which exhibit distinct physical properties, a virtual spring capable of applying the elastic modulus within the tetrahedron was developed. A virtual spring was established between the centroid of the tetrahedron and each vertex. By adjusting the normalized coefficients while preserving the overall deformation, various physical properties can be demonstrated [18].
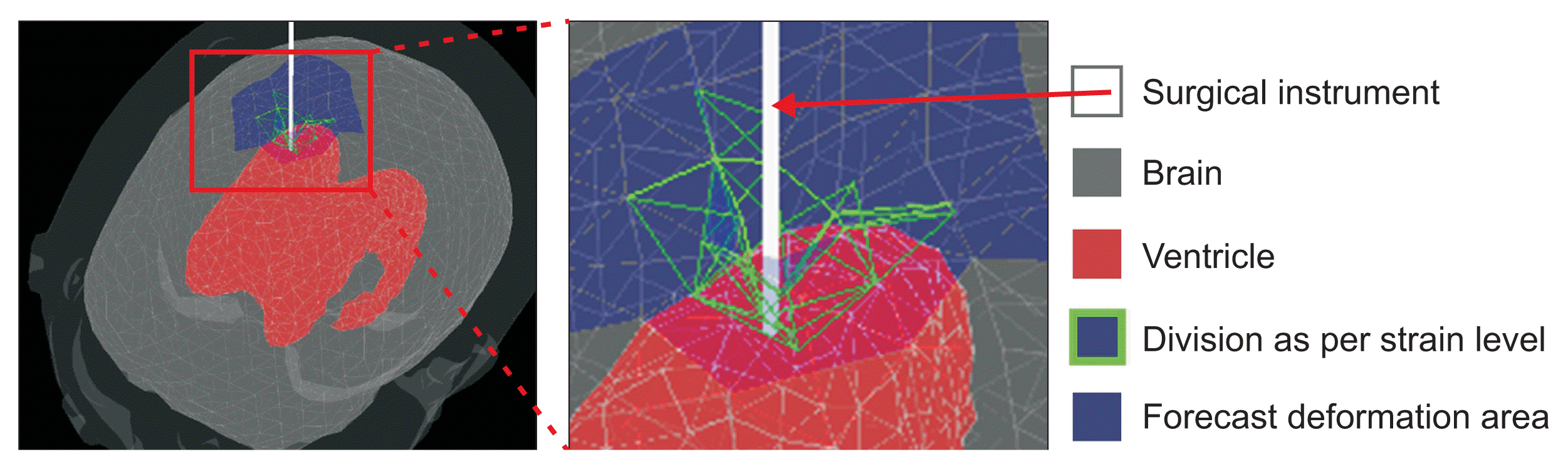
Precisely detecting a collision and the resulting deformation is necessary for modeling brain deformation during the process of inserting surgical instruments into a target ventricle. However, issues may arise due to an increase in computational load and a decrease in simulation speed when detecting detailed collision and deformation effects across the entire brain area. In this paper, we define the deformation space using a sphere tree [28] and enhance computational efficiency by utilizing the predicted deformation space based on the degree of deformation caused by the surgical instrument. The collision detection area consists of a spherical shape optimized for processing the brain’s rounded shape. This range is hierarchically narrowed down to enable rapid detection of collisions with surgical instruments.
The predicted deformation space represents the area where deformation occurs due to the surgical instrument. This region is divided by comparing the average change in the tetrahedrons of the affected area with the average change in those of the entire brain region. Collisions can be resolved more frequently than in other spaces to minimize penetration by surgical instruments. Deformation accuracy is enhanced by reducing the unit time (Δt) and adjusting the number of constraint iterations (Figure 4).
In this study, experiments were conducted using a personal computer equipped with an Intel i7-11700 processor (3.6 GHz), 16 GB of RAM, and an NVIDIA GeForce GTX 1660 graphics card. The data utilized in the experiments, which included a phantom experiment and an AR ventriculostomy in a real surgical environment, were derived from computed tomography images of two patients in need of ventriculostomy. This data was provided by Yonsei University Severance Hospital.
The model depicted in Figure 5 was created using 3D printing for the phantom experiment. The skin area functioned as a reference point for alignment and was consequently utilized in its original form. A simplified, drawer-like model was chosen for the brain and ventricle to facilitate reusability and simplify the verification of experimental results. A gelatin material with properties similar to those of brain tissue was selected for the interior of the brain.
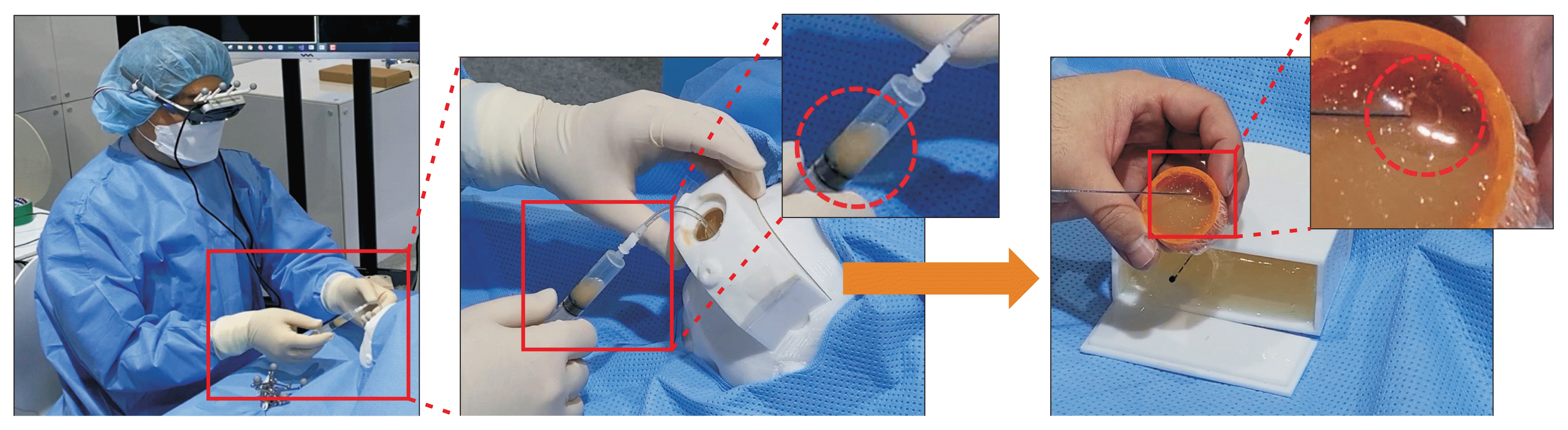
The phantom model experiment was conducted as follows. Prior to surgery, the direction and depth of the surgical instrument’s insertion were planned, the work area and insertion paths were marked on the 3D model, and an infrared marker-based AR surgical environment was established. At the beginning of the operation, the operator entered the corresponding points to align the phantom model with the 3D brain model. Once the alignment was complete, the insertion path, entry angular error relative to the current surgical instrument, and distance to the target were visualized on the smart glasses, as depicted in Figure 6. The zoom navigation feature in the bottom left corner of the screen enables the user to examine the structure near the surgical instrument and the deformation of the 3D brain model caused by the surgical instrument (Figure 6B).
The tasks evaluated involved inserting the surgical instrument into the ventricle using only the navigation information provided by the smart glasses and monitoring the drainage of cerebrospinal fluid. In Figure 7, the central image illustrates the process of cerebrospinal fluid drainage through the inserted catheter, guided by the AR system. The figure on the right displays a container of cerebrospinal fluid situated within the phantom model, and also demonstrates the process of verifying that the catheter has penetrated the upper portion of the container. These tasks were successfully completed, as evidenced by the drainage (Figure 7).
AR ventriculostomy was performed in an actual surgical environment after the Institutional Review Board approval (No. 4-2020-1034) at Yonsei University Health System, Severance Hospital. Written informed consents were obtained. While the procedure was similar to that of the phantom model experiment, a catheter was initially inserted into the ventricle according to conventional surgical guidelines using a commercial navigation system (Brainlab, Munich, Germany) to ensure patient safety. After placing the ventricular catheter, the AR system’s guidance, utilizing a navigated disposable stylet, was introduced into the ventricular catheter, and our system performed precisely as planned.
Figure 8 shows that the proposed AR system successfully reached the target point, the foramen of Monro, from Kocher’s point when inserted along the conduit path recommended by the commercial navigation system. This confirms its clinical applicability and validity.
The image processing speed was determined by averaging the simulation speeds from repeated measurements for a 3D model of the brain and surgical instrument within a virtual space. The average was calculated after 10 deformations with surgical instruments, and this set was repeated five times. The soft-body simulation speed, which included collision detection, soft-body deformation, and rendering times, was measured. The data used in this study’s experiments were taken from an actual surgical environment. A smaller number of elements in the model resulted in a faster execution time. However, in this study, we used a model with the resolution adjusted so that the average spacing between the model’s vertices was within 3 mm. This was done considering that the diameter of the catheter used for ventriculostomy was 9–10 Fr (approximately 3 mm). The brain model, including the ventricle region, consisted of 37,336 elements. The experiment demonstrated an average speed of 18.78 fps (53.24 ms).
The tracking speed of surgical instruments and the rendering of smart glasses may appear slower compared to the real-time performance of over 30 fps in AR systems, due to the rate of soft-body deformation. To counteract this, each process was calculated as an independent thread, and information was updated based on the smart glasses’ rendering cycle. The soft-body deformation information that was closest to the current rendering point was chosen for visualization, ensuring that the AR system’s speed was not affected. Two clinicians were asked to qualitatively evaluate the phantom experiment, and both reported no discomfort in terms of speed.
Table 1 shows the differences in soft-body simulation speeds between the method proposed in this paper and those found in existing studies [14,17,29,30]. Furthermore, studies employing the proposed method were compared to those simulating soft-body deformation caused by surgical instruments. There are discrepancies in the number of elements in each study’s 3D model used for speed measurement. Consequently, the data resolution was adjusted to compare the speed of the method presented in this paper with those of existing methods. Fukuhara et al. [14] utilized data with a number of elements most similar to that in this paper. However, it took the longest time (700 ms) due to the use of FEM for deformation. In the study by Yang et al. [29], the element type was different, but the execution time was lengthy considering the number of elements. Pan et al. [17] conducted PBD-based deformation and demonstrated a rapid performance of less than 10 ms. Nonetheless, comparing the results of Pan et al.’s method with the study results in this paper proved challenging due to differences in simulation procedures. The method by Pan et al. [17] involved simulating the cutting of a large area, allowing for the simulation to be conducted with a smaller number of elements. However, this study required a higher model resolution since it focused on a procedure involving the insertion of surgical instruments into a localized area.
AR technology is gaining popularity due to its ability to merge real-world perceptions with virtual images, providing an enhanced interactive experience and immersion [1]. AR has been utilized in various medical fields, including brain surgery. However, previous studies [6–8] have limited the use of AR to overlaying anatomical structures, without considering potential brain deformation during surgery. In this paper, we propose an AR-based brain ventriculostomy simulation technique that visualizes a 3D model of brain deformation caused by the movement of surgical instruments, using a PBD physical deformation method on preoperative images. To achieve a realistic representation, we employed a hybrid geometric model that combines both high-resolution mesh and multiresolution tetrahedron models, while reducing the simulation computation load. An infrared camera was used to track smart glasses and surgical instruments. We applied various constraints to the PBD model to represent brain deformation caused by surgical instruments and heterogeneous characteristics, such as the brain and ventricle.
We conducted two experiments to assess the effectiveness of the AR ventriculostomy system. In the phantom experiment, surgical instruments were inserted into the phantom model using only the navigation information displayed on the smart glasses, and the drainage of cerebrospinal fluid was examined. The clinician identified the three-dimensional structure of the ventricle as it was deformed by the surgical instrument and confirmed that the instrument was accurately guided to the target point. The soft body deformation speed was 18.78 fps. Although this speed did not reach the real-time threshold of 30 fps, it was synchronized with the rendering cycle of the smart glasses. Two clinicians were asked to provide a qualitative evaluation of the phantom experiment, and both reported that they did not experience any discomfort in terms of speed.
In the actual surgical environment, the catheter was first inserted using a commercially available navigation system (Brainlab) to ensure patient safety. Subsequently, the disposable stylet was inserted under the guidance of the AR system described in this paper. Moreover, the surgical plan created by the commercial navigation system was consistent with the plan of the developed system for clinical patients in the real surgical environment. Consequently, it was confirmed that the system could be applied to clinical practice.
The results of this study indicate that additional research is necessary to enhance the speed of soft body deformation. Moreover, a multiresolution tetrahedron model was employed to increase the speed, while a hierarchical sphere tree was utilized for rapid collision detection. Despite these efforts, real-time processing performance was not attained. By synchronizing with the smart glasses’ rendering cycle, user discomfort resulting from the slow speed was minimized. However, this synchronization could potentially impact the precision of the soft body deformation.
Acknowledgments
This work was partly supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. 2020R1A2C1102727). This research was partly supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (No. 2020R1A6A3A01099507). This research was supported by the MSIT (Ministry of Science and ICT), Korea, under the National Program for Excellence in SW (No. 2018-0-00209) supervised by the IITP (Institute of Information & communications Technology Planning & Evaluation).
References
1. Chen Y, Wang Q, Chen H, Song X, Tang H, Tian M. An overview of augmented reality technology. J Phys Conf Ser. 2019; 1237(2):022082. https://doi.org/10.1088/1742-6596/1237/2/022082.

2. Mishra R, Narayanan MD, Umana GE, Montemurro N, Chaurasia B, Deora H. Virtual reality in neurosurgery: beyond neurosurgical planning. Int J Environ Res Public Health. 2022; 19(3):1719. https://doi.org/10.3390/ijerph19031719.

3. Bhushan S, Anandasabapathy S, Shukla R. Use of augmented reality and virtual reality technologies in endoscopic training. Clin Gastroenterol Hepatol. 2018; 6(11):1688–91. https://doi.org/10.1016/j.cgh.2018.08.021.

4. Park SM, Kim HJ, Yeom JS, Shin YG. Spine surgery using augmented reality. J Korean Soc Spine Surg. 2019; 26(1):26–32. https://doi.org/10.4184/jkss.2019.26.1.26.

5. Chen Y, Wang Q, Chen H, Song X, Tang H, Tian M. An overview of augmented reality technology. J Phys Conf Ser. 2019; 1237(2):022082. https://doi.org/10.1088/1742-6596/1237/2/022082.

6. Cabrilo I, Bijlenga P, Schaller K. Augmented reality in the surgery of cerebral arteriovenous malformations: technique assessment and considerations. Acta Neurochir (Wien). 2014; 156(9):1769–74. https://doi.org/10.1007/s00701-014-2183-9.

7. Besharati Tabrizi L, Mahvash M. Augmented reality-guided neurosurgery: accuracy and intraoperative application of an image projection technique. J Neurosurg. 2015; 123(1):206–11. https://doi.org/10.3171/2014.9.JNS141001.

8. Watanabe E, Satoh M, Konno T, Hirai M, Yamaguchi T. The trans-visible navigator: a see-through neuronavigation system using augmented reality. World Neurosurg. 2016; 87:399–405. https://doi.org/10.1016/j.wneu.2015.11.084.

9. Gerard IJ, Kersten-Oertel M, Petrecca K, Sirhan D, Hall JA, Collins DL. Brain shift in neuronavigation of brain tumors: a review. Med Image Anal. 2017; 35:403–20. https://doi.org/10.1016/j.media.2016.08.007.

10. Vigo V, Tassinari A, Scerrati A, Cavallo MA, Rodriguez-Rubio R, Fernandez-Miranda JC, et al. Ideal trajectory for frontal ventriculostomy: radiological study and anatomical study. Clin Neurol Neurosurg. 2022; 217:107264. https://doi.org/10.1016/j.clineuro.2022.107264.

11. Amoo M, Henry J, Javadpour M. Common trajectories for freehand frontal ventriculostomy: a systematic review. World Neurosurg. 2021; 146:292–7. https://doi.org/10.1016/j.wneu.2020.11.065.

12. Hamze N, Peterlik I, Cotin S, Essert C. Preoperative trajectory planning for percutaneous procedures in deformable environments. Comput Med Imaging Graph. 2016; 47:16–28. https://doi.org/10.1016/j.compmedimag.2015.10.002.

13. Bayer S, Maier A, Ostermeier M, Fahrig R. Intraoperative imaging modalities and compensation for brain shift in tumor resection surgery. Int J Biomed Imaging. 2017; 2017:6028645. https://doi.org/10.1155/2017/6028645.

14. Fukuhara A, Tsujita T, Sase K, Konno A, Jiang X, Abiko S, et al. Proposition and evaluation of a collision detection method for real time surgery simulation of opening a brain fissure. ROBOMECH J. 2014; 1:6. https://doi.org/10.1186/s40648-014-0006-7.

15. Forte AE, Galvan S, Dini D. Models and tissue mimics for brain shift simulations. Biomech Model Mechanobiol. 2018; 17(1):249–61. https://doi.org/10.1007/s10237-017-0958-7.

16. Muller M, Heidelberger B, Hennix M, Ratcliff J. Position based dynamics. J Vis Commun Image Represent. 2007; 18(2):109–18. https://doi.org/10.1016/j.jvcir.2007.01.005.

17. Pan J, Yan S, Qin H, Hao A. Real-time dissection of organs via hybrid coupling of geometric metaballs and physics-centric mesh-free method. Vis Comput. 2018; 34:105–16. https://doi.org/10.1007/s00371-016-1317-x.

18. Pan J, Bai J, Zhao X, Hao A, Qin H. Real-time haptic manipulation and cutting of hybrid soft tissue models by extended position-based dynamics. Comput Anim Virtual Worlds. 2015; 26(3–4):321–35. https://doi.org/10.1002/cav.1655.

19. Romeo M, Monteagudo C, Sanchez-Quiros D. Muscle and fascia simulation with extended position based dynamics. Comput Graph Forum. 2020; 39(1):134–46. https://doi.org/10.1111/cgf.13734.

20. Mortensen EN, Barrett WA. Interactive segmentation with intelligent scissors. Graph Models Image Process. 1998; 60(5):349–84. https://doi.org/10.1006/gmip.1998.0480.

21. Lorensen WE, Cline HE. Marching cubes: a high resolution 3D surface construction algorithm. ACM SIGGRAPH Comput Graph. 1987; 21(4):163–9. https://doi.org/10.1145/37402.37422.

22. Allard J, Cotin S, Faure F, Bensoussan PJ, Poyer F, Duriez C, et al. SOFA: an open source framework for medical simulation. Stud Health Technol Inform. 2007; 125:13–8.
23. Kim J, Kwon K, Shin BS. Adaptive tetrahedral mesh generation for non-uniform soft tissue simulation. Hum Cent Comput Inf Sci. 2021; 11:29. https://doi.org/10.22967/HCIS.2021.11.029.

24. Muller M, Gross MH. Interactive virtual materials. In : Proceedings of the Graphics Interface 2004 Conference; 2004 May 17–19; London, Ontario, Canada. p. 239–46.
25. OptiTrack. Motive: optical motion capture software [Internet]. Corvallis (OR): NaturalPoint Inc;c2023. [cited at 2023 Jul 21]. Available from: https://optitrack.com/software/motive/.
26. Kim JD. Application of augmented reality for surgical guidance [thesis]. Seoul, Korea: Seoul University;2020.
27. Kelager M, Niebe S, Erleben K. A triangle bending constraint model for position-based dynamics. In : Proceedings of the Workshop on Virtual Reality Interaction and Physical Simulation; 2010 Nov 11–12; Copenhagen, Denmark. p. 31–7. https://doi.org/10.2312/PE/vriphys/vriphys10/031-037.

28. Palmer IJ, Grimsdale RL. Collision detection for animation using sphere-trees. Comput Graph Forum. 1995; 14(2):105–16. https://doi.org/10.1111/1467-8659.1420105.

29. Yang C, Li S, Wang L, Hao A, Qin H. Real-time physical deformation and cutting of heterogeneous objects via hybrid coupling of meshless approach and finite element method. Comput Anim Virtual Worlds. 2014; 25(3–4):421–33. https://doi.org/10.1002/cav.1594.

30. Xu L, Lu Y, Liu Q. Integrating viscoelastic mass spring dampers into position-based dynamics to simulate soft tissue deformation in real time. R Soc Open Sci. 2018; 5(2):171587. https://doi.org/10.1098/rsos.171587.

Figure 1
Augmented reality (AR)-based ventriculostomy simulation process. IR: infrared, 3D CT: three-dimensional computed tomography.
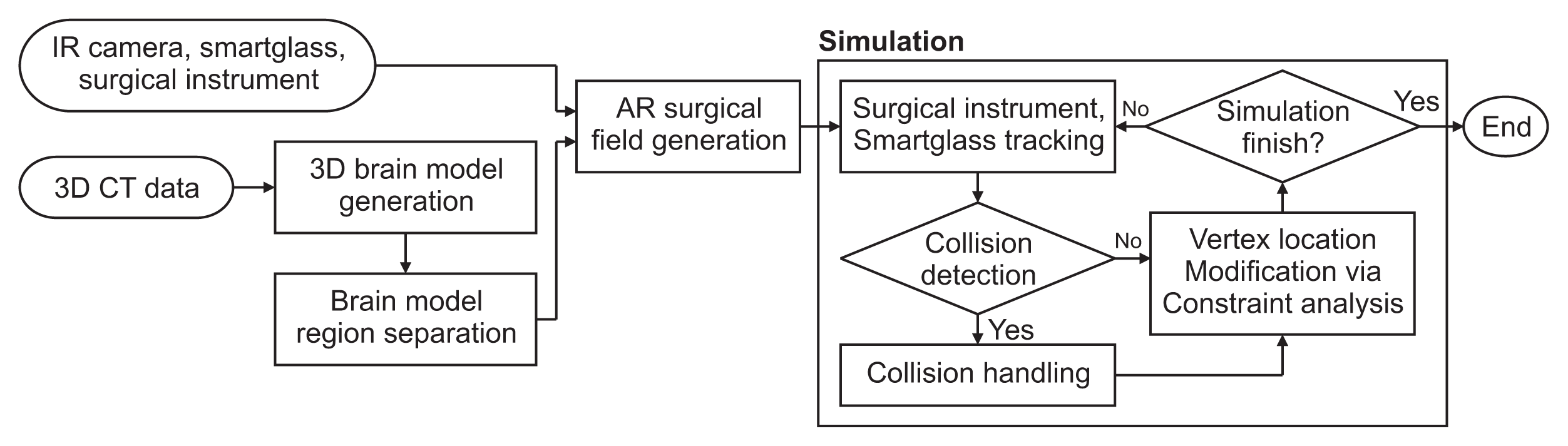
Figure 3
Setting and manual matching of response points. (A) Feature points in virtual space. (B) Feature points in real space.
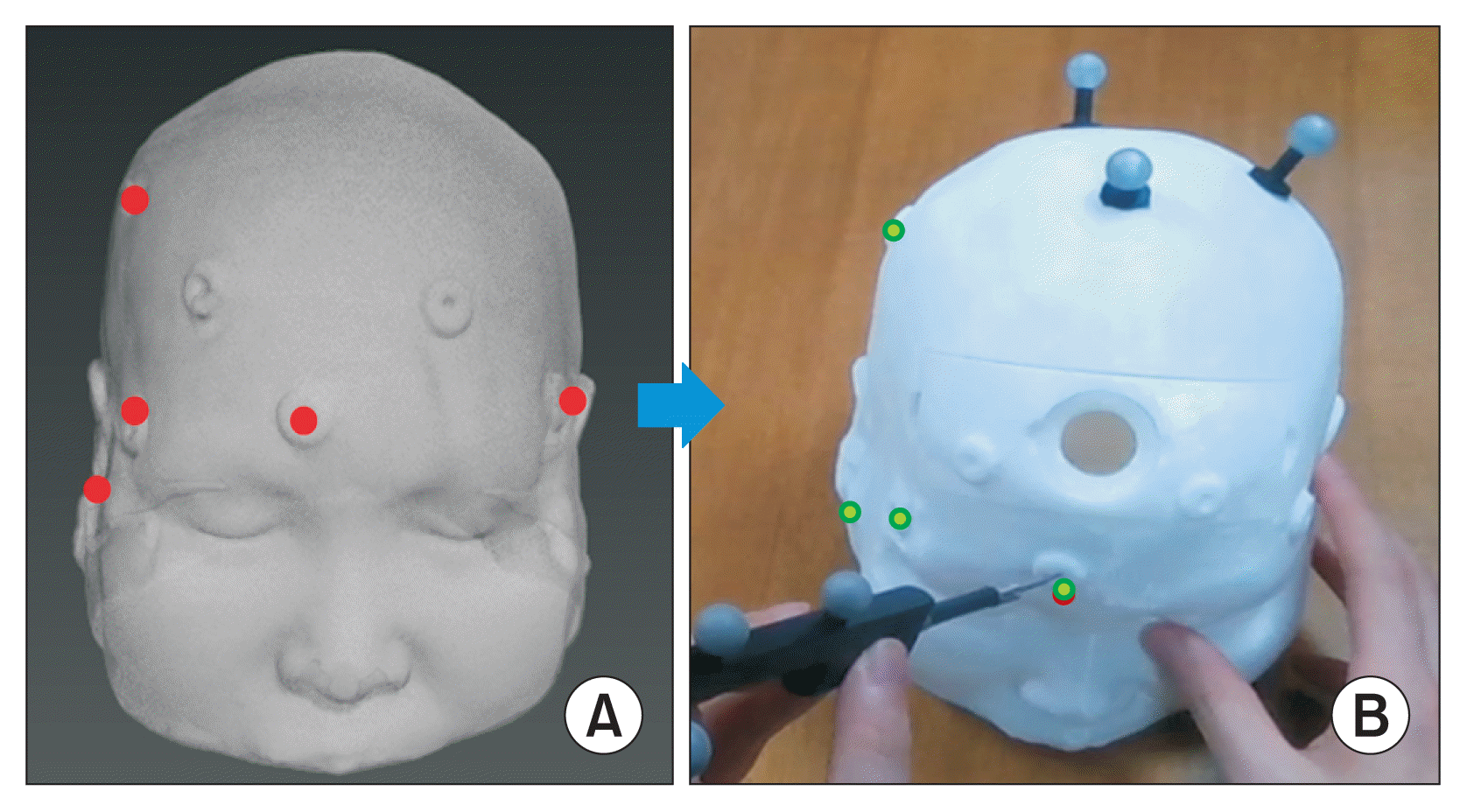
Figure 6
Smart glasses screen. (A) Multiplanar reconstruction images, (B) zoom navigation, and (C) entry angle error of the surgical instrument.
Table 1
Comparison between the proposed method and existing studies
| Study | Method | 3D model | Elements | Element type | Time (ms) |
|---|---|---|---|---|---|
| Fukuhara et al. [14] | FEM | Brain | 34,401 | Tetrahedron | 700 |
|
|
|||||
| Yang et al. [29] | FEM | Steak | 6,272 | Hexahedron | 25.2 |
|
|
|||||
| Pan et al. [17] | PBD | Liver | 570 | Particle | 6.25 |
| Spleen | 466 | Particle | 2.65 | ||
|
|
|||||
| Xu et al. [30] | PBD + mass spring | Liver, gallbladder | 650 | Particle | 24.26 |
|
|
|||||
| Proposed method | PBD | Brain, ventricle | 65,691 | Tetrahedron | 85.32 |
| Brain, ventricle | 37,336 | Tetrahedron | 53.24 | ||
| Brain, ventricle | 20,677 | Tetrahedron | 34.92 | ||
| Brain, ventricle | 5,824 | Tetrahedron | 17.51 | ||
| Brain, ventricle | 612 | Tetrahedron | 7.14 | ||




 PDF
PDF Citation
Citation Print
Print





 XML Download
XML Download