Abstract
Objective
To investigate sex-specific correlations between the dimensions of permanent canines and the anterior Bolton ratio and to construct a statistical model capable of identifying the sex of an unknown subject.
Methods
Odontometric data were collected from 121 plaster study models derived from Caucasian orthodontic patients aged 12–17 years at the pretreatment stage by measuring the dimensions of the permanent canines and Bolton's anterior ratio. Sixteen variables were collected for each subject 12 dimensions of the permanent canines, sex, age, anterior Bolton ratio, and Angle’s classification. Data were analyzed using inferential statistics, principal component analysis, and artificial neural network modeling.
Results
Sex-specific differences were identified in all odontometric variables, and an artificial neural network model was prepared that used odontometric variables for predicting the sex of the participants with an accuracy of > 80%. This model can be applied for forensic purposes, and its accuracy can be further improved by adding data collected from new subjects or adding new variables for existing subjects. The improvement in the accuracy of the model was demonstrated by an increase in the percentage of accurate predictions from 72.0–78.1% to 77.8–85.7% after the anterior Bolton ratio and age were added.
In forensic practice, the identification of human remains is common.1 Odontometric measurements represent an easy way to collect data on the morphological variations in human dentition.2 Information about age, sex, and race can be obtained based on differences in tooth dimensions. The ability of a model to determine sex depends on the expression of certain characteristics of males versus females in relation to random deviations from the mean values within individual groups.3
Different statistical models have different degrees of success in determining sex depending on the type and amount of input data. Simple odontometric variables, such as the mesiodistal (MD), vestibular-oral (VO), and cervical-incisal (CI) dimensions of the teeth, show sexual dimorphism to some extent and can be used to determine the sex of unknown subjects.4,5 The main advantage of these variables is their fast and easy collection compared with other sophisticated and expensive methods. In addition to simple tests of inferential statistics that compare arithmetic means around which the values of odontometric variables of male and female subjects are grouped, data can be processed using more advanced statistical models, such as principal component analysis (PCA) or artificial neural network models.6,7 The PCA is commonly used in models that tend to reduce the amount of data collected in a smaller number of dimensions. Such analysis seeks to reduce the number of variables by retaining the largest possible amount of information contained in them. An example of a successfully applied PCA is the development of a model for sex determination based on the spectrometric analysis of hard dental tissues.8
Artificial neural networks are an alternative to the PCA model.9 This model can identify sex-related differences in individual variables based on data from respondents of known sex and apply learning to predict the sex of unknown respondents.10 The advantage of this model over the PCA model is the targeted search for sex-specific information hidden in many variables, unlike PCA, the primary goal of which is to reduce data space by reducing them to major components that do not necessarily carry useful information on sexual dimorphism.11
In the present study, odontometric data of the permanent canines (CI, MD, and VO) and anterior Bolton ratio were analyzed to identify sex-related differences. Interferential statistical analysis initially identified sex-related differences and their expression with respect to different odontometric variables. Odontometric data were then used to develop statistical models to determine the sex of an unknown subject. For this purpose, two approaches were applied: the PCA method and the artificial neural network model. The relative advantages and disadvantages of the individual models were interpreted, and the models were further optimized to achieve the highest precision for sex determination.
This study aimed to investigate the correlation between the dimensions of the permanent canines and the anterior Bolton ratio with sex differences in tooth dimensions. Furthermore, sex-specific differences in the aforementioned variables were used to prepare a statistical model to determine the sex of an unknown subject.
This study was approved by the Ethics Committee of the School of Dental Medicine, University of Zagreb (decision number: 05-PA-30-XVIII-6/2020).
Odontometric data were collected using 121 plaster study models from the archives of the Department of Orthodontics, School of Dental Medicine, University of Zagreb. The models had been prepared between 2016 and 2021. The inclusion criteria were complete permanent dentition and no missing teeth. All participants were Caucasian and had consented to the storage and use of their study models for research purposes as part of the usual informed consent practice in the Department of Orthodontics. The researchers were blinded to the patients’ personal data at all stages of the study and statistical analysis.
The dimensions of the permanent canines (CI, MD, and VO) and Bolton front ratios were measured for each study model. Generally, orthodontic patients are more likely to have greater Bolton discrepancies than individuals with normal occlusions; for example, the maxillary lateral incisors may be small.
Measurements were performed by a resident of the Department of Orthodontics (NM) using a digital movable measuring device with an accuracy of 0.1 mm. All variables were measured three times, and the mean value of the measurements was used for the research. Sixteen variables were collected for each subject: 12 dimensions of the permanent canines (4 teeth × 3 dimensions), sex, age, anterior Bolton ratio, and Angle’s classification data.
The normality of the distribution was verified using the Kolmogorov–Smirnov test and normal Q-Q diagrams. The mean values of the odontometric variables between male and female subjects were compared using an independent observations t-test. Odontometric variables and anterior Bolton ratios were compared among different Angle malocclusion using one-way ANOVA with Bonferroni post-hoc adjustment for multiple comparisons. The overall level of significance was set at p < 0.05. PCA was performed using varimax rotation, separately for each sex and in a “joint” model accounting for both sexes. Two different PCA approaches were tested: (I) including only 12 odontometric variables (four permanent canines × three dimensions) and (II) including the anterior Bolton ratio. Principal components with eigenvalues higher than 1 were retained, resulting in a PCA model with the first two principal components for approach (I) and the first three principal components for approach (II). Sex-related differences in the first two principal components were tested using a t-test for independent observations. An artificial neural network model for sex determination was prepared using a multilayer perceptron network with a varying number of layers (one or two hidden layers) and varying activation functions of the hidden layers (hyperbolic tangent or sigmoid) and the output layer (identity, softmax, tangent, or sigmoid). Training was performed using error backpropagation. Two versions of artificial neural networks for sex determination were prepared: I) including only 12 odontometric variables, and (II) including the anterior Bolton ratio and Angle classification. The available sample of 121 participants was randomly allocated in a 70:30 ratio for training and testing. The capabilities of the individual models for correct classification were compared using receiver operating curves. All statistical analyses were performed using IBM SPSS, Statistics for Windows version 25 (IBM Corp., Armonk, NY, USA).
Normality tests showed no significant deviation from normal distribution in most groups. Although the Kolmogorov–Smirnov and Shapiro–Wilk tests showed a significant deviation from normal distribution in several groups, the deviation does not represent an obstacle to the application of parametric statistical analysis in a balanced design.
The mean values of the individual odontometric variables of the permanent canines and the results of the t-test for the comparison between male and female participants are summarized in Table 1. For each variable, a significantly lower mean value was observed for women than for men. The measured values (6.4–9.1 mm) were significantly higher among the male participants. The CI dimension was the largest, followed by the VO and MD dimensions.
There were no statistically significant differences in any odontometric variables, and the values of the partial eta squares and observed power were relatively low. The observed test power was generally < 32%. A t-test indicated no significant difference in the anterior Bolton ratio between the sexes (p = 0.585).
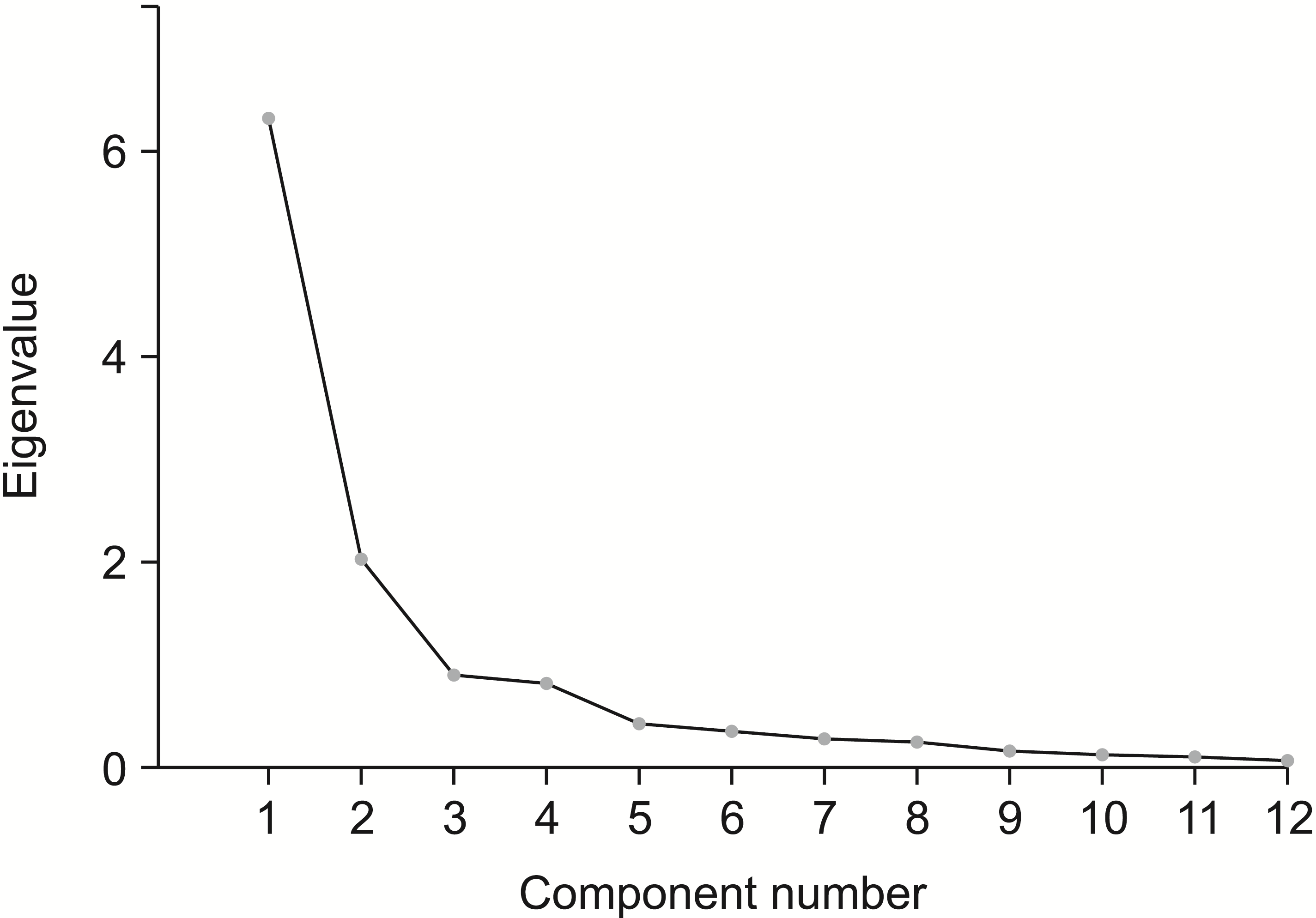
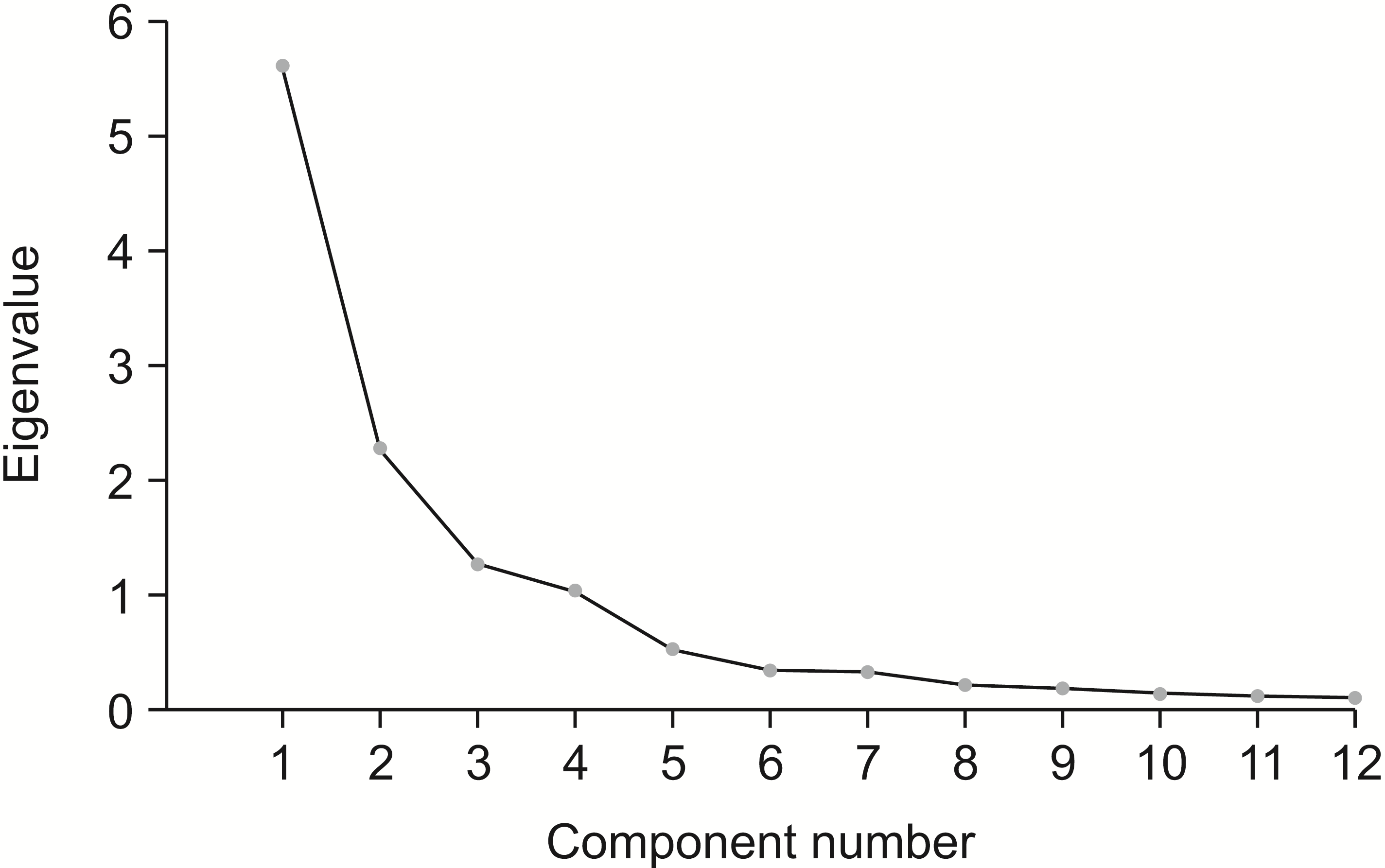
A scree diagram showing the eigenvalues for the individual components of the PCA model based on participants of both sexes is shown in Figure 1. Most of the variance was described by the first two main components, whereas the third component had an intrinsic value lesser than 1.
By visualizing the odontometric variables in the rotated space of the first two main components, a description of their interdependencies was obtained, represented by two-dimensional spatial relations. A view of the rotated spaces of the first two main components in Figure 2 shows how the CI variables for the four permanent canines are grouped into one cluster, the VO variables into the second cluster, and the MD into the third cluster. Variables grouped within a single cluster were more strongly interrelated than those belonging to other clusters. In addition, clusters that were more distant from each other (e.g., CI and MD, which were more distant from each other than CI and VO) were more independent.
Analogous to the previously shown scree diagram for the PCA model based on all subjects, an additional scree diagram for the eigenvalues of the PCA model components limited to male participants is shown in Figure 3. In this model, the majority of the variance belongs to the first two main components, whereas the third component has an intrinsic value lower than 1.
The rotated spaces of the first two main components of the male-based PCA model (Figure 4) showed similar relationships between odontometric variables as previously shown for the PCA model based on both sexes. The CI, VO, and MD variables formed separate clusters, and VO and MD were more interrelated than CI and VO.
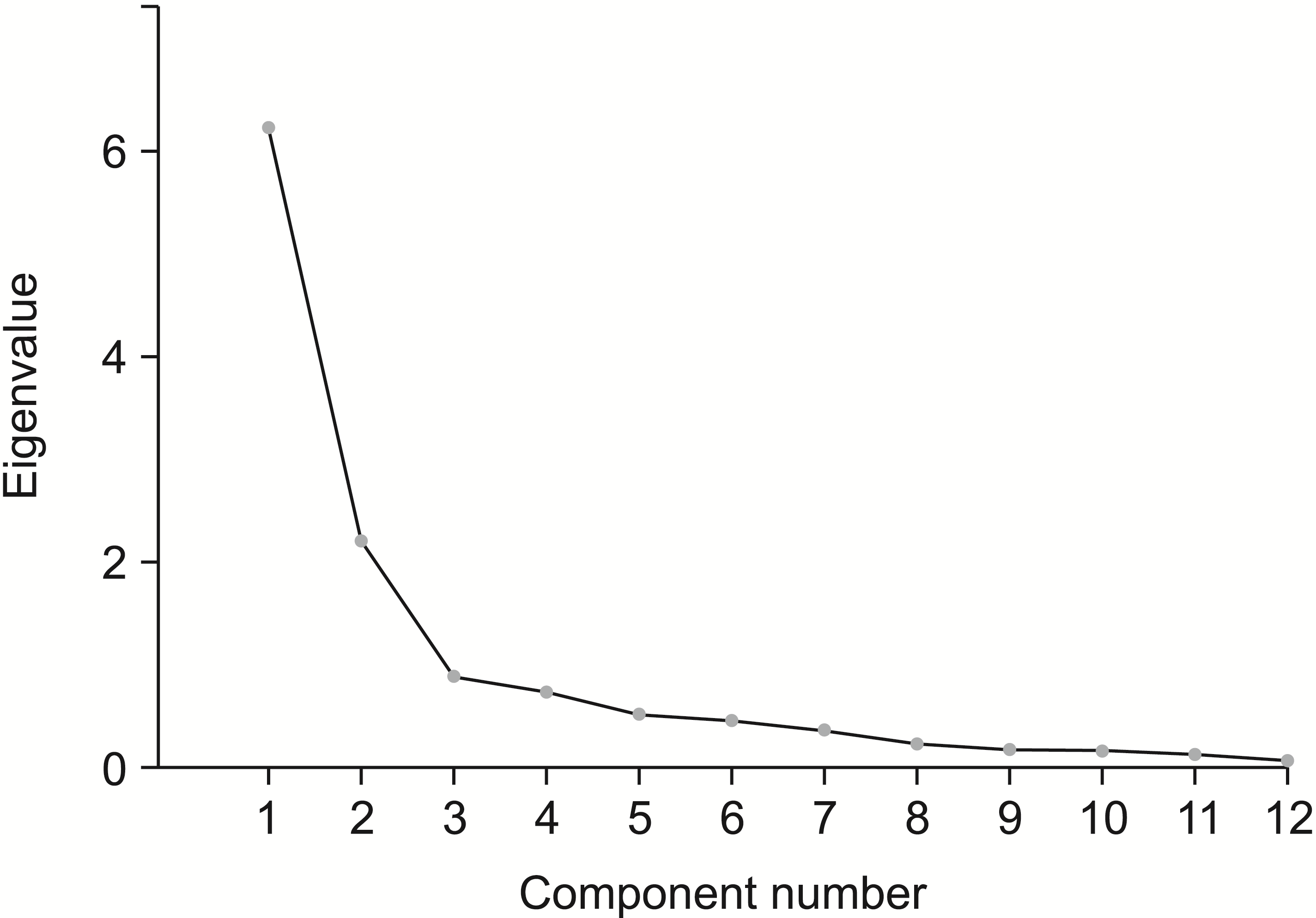
A scree diagram for the PCA model based on female participants is shown in Figure 5. The first two main components accounted for most of the variance, and although the third main component had an intrinsic value greater than 1, it was omitted from the analysis to ensure that the PCA model based on female participants was comparable with the previous two PCA models (the one for both sexes and that for males).
The relationships of odontometric variables in the rotated space of the first two main components for the PCA model based on female participants differed from those of the previous two PCA models because the clusters of the VO and CI variables were significantly closer to each other (Figure 6). Moreover, there were overlaps between the VO and CI variables, and they formed one common cluster. The VO variables were significantly further from the MD variables than in the previous two PCA models. These results indicate that there is a more pronounced association between VO and CI variables among females than among males.
Because the first three main components were retained in the PCA with the anterior Bolton ratio included, the relationships of the odontometric variables in the rotated space are shown three-dimensionally in Figure 7A. The variables CI, VO, and MD were grouped into clusters in a similar manner to the previously presented PCA analyses, whereas the anterior Bolton ratio differed according to the third main component, which is visible in the graph as a shift along the z-axis. The relationships of the odontometric variables in the PCA model with the anterior Bolton ratio observed in male subjects (Figure 7B) were similar to the relationships in the common model for both sexes. The CI, VO, and MD variables were located in the space of the first two principal components and offset from the anterior Bolton ratio in the direction of the third principal component. The grouping of CI, VO, and MD is visible as in the common model for both sexes, and the relative distances of the individual clusters are also similar; CI and MD variables are the farthest from each other, whereas VO variables are located between clusters of CI and MD variables. In contrast to the two previously presented PCA models (for both sexes together and for males), the female-based model (Figure 7C) shows less well-defined clusters of VO and CI variables with significant overlaps. However, all four MD variables were located extremely close together, indicating a stronger association in females.
To visually assess the discriminant potential of the first two main components for the classification of respondents by sex, a graphical presentation was prepared in the form of a scatter plot in which each point represented one respondent (Figure 8). In this diagram, the x–y coordinates represent the values of the first two components for each subject. It is evident that, despite the statistically significant differences in the values of the first main component between the sexes, there is a marked overlap between male and female respondents, that is, there are no clearly defined clusters that would classify respondents into a particular sex. Female respondents are represented more on the left (lower values of the first main component), while male respondents are represented more on the right (higher values of the first main component); however, there is a pronounced overlap in the middle. For the respondents in this area, the PCA model did not correctly identify participant sex.
The presentation of data of individual participants in a three-dimensional space for the first three main components of the PCA model, which included 12 odontometric variables in addition to the Bolton ratio, also showed an insufficient ability to classify participants by sex (Figure 9).
In this presentation, separation with respect to the first main component (x-axis) was still dominant, with a higher density of female subjects on the left side and males on the right side of the x-axis. The remaining two main components contributed almost nothing to sex segregation.
A model that optimally classified participants according to sex was selected. This model contained one hidden layer. The activation function of the hidden layer was a hyperbolic tangent, whereas the softmax function was applied to activate the output layer. Of the respondents, 78.1% were correctly classified, and 72.0% showed accurate classification during testing. Analogous to the testing of 16 neural network models based on odontometric variables, an additional 16 models (eight single-layer and eight multilayer models with different combinations of activation functions) were prepared, which also included the anterior Bolton ratio and age.
The inclusion of these two additional variables increased the classification capacity of the neural network, and the optimized model correctly classified 85.7% of respondents in the learning phase, whereas in the testing phase, the success rate of correct classification was 77.8%. Similar to models based only on odontometric variables, models with the anterior Bolton ratio and age included an optimized model with one hidden layer, a hyperbolic tangent as a hidden layer activation function, and a softmax function to activate the output layer. The model of the optimal neural network, which includes the anterior Bolton ratio and the age of the participants, is shown in Figure 10A and 10B.
Correlations between the dimensions of permanent canines, anterior Bolton ratio, and sex-specific differences in tooth dimensions were investigated in this study. The identified sex-specific differences in odontometric data were used to prepare the PCA models and artificial neural networks. Statistically significant differences were found in the mean values of individual odontometric variables of the permanent canines between the male and female participants. Each of the 12 odontometric variables was significantly different between sexes. This finding is consistent with previously published studies documenting sexual dimorphism in permanent human canines.12-14 Some studies found no differences between male and female participants, which in most cases can be attributed to an insufficient sample size, reducing the likelihood of detecting a significant effect through statistical analysis.15,16
No statistically significant differences were found on comparing the values of the odontometric variables based on the Angle malocclusion classification. There was also no statistically significant association between the anterior Bolton ratio and Angle malocclusion. However, differences between malocclusions based on Angle’s classification were expected.17-19 It is likely that the sample size of this study was insufficient to identify differences between Angle’s malocclusion classes. An analogous conclusion was drawn in other studies in which a small number of respondents led to low statistical power and an inability to detect sex-specific differences.20,21
The first two principal components carried the largest share of information on the variation in all 12 odontometric variables. The mean values of the first two principal components were compared between males and females; for the first principal component, a highly significant difference between the sexes was found (p < 0.001), whereas for the second principal component, there was no statistically significant difference. With significant differences in the mean values of the first major component between the sexes, the male participants had positive values and female participants had negative values, with the 95% confidence intervals not overlapping. This finding suggests that the first major component may be useful for separating respondents by sex. However, the scatter plot for the values of the first two principal components for individual subjects shows that this is not the case; that is, despite statistically significant differences between males and females, there were marked overlaps when observing individual subjects. This shows that simple hypothesis tests (t-test or ANOVA) can provide a statistically significant result in the case of a large sample, despite the existence of large overlaps between groups. Therefore, the statistically significant difference between the mean values of odontometric variables, which has often been identified in different studies,22-24 does not necessarily indicate their practical applicability for the identification of respondents by sex.
To construct an artificial neural network model that can classify individuals by sex, based on the odontometric variables of permanent canines, single-layer and multilayer perceptron networks with different activation functions were examined.25 A single-layer perceptron network comprises one input layer, one hidden layer, and one neuron output layer. Neurons communicate only between layers, and there are no interneural connections within the same layer. Similarly, a two-layer perceptron network has two hidden layers that communicate with each other. By examining the different structures of neural networks and activation functions, operational curves were obtained that showed the relationship between the sensitivity and specificity of the classification of subjects by sex for a particular neural network.26 In other words, increasing the sensitivity of the network should reduce its specificity as little as possible so that the model produces as few false-positive results as possible. This relationship between sensitivity and specificity was measured by the area under the operating characteristic curve; this area should be as large as possible for the classification to be successful.27
The anterior Bolton ratio introduced additional information into the model that was not included in the initial 12 odontometric variables; information on the age of the subjects probably addressed the changes in tooth dimensions that occur with aging due to wear.28 A similar precision of the classification of respondents by sex (86% correct) was shown by Vodanović et al.13 on using a combination of craniofacial and odontometric data. This study achieved similar precision but used only odontometric variables, indicating the high efficiency of the neural network model for extracting information on sexual dimorphism and its applicability for sex determination. To place the model of sex determination presented in this paper in the context of other research using odontometric data to predict sex, it can be mentioned that their ability to correctly classify individuals by sex ranges from 60% to 88%.12,29-31
It should be noted that the dimensions of the teeth are characteristic of the observed population, and therefore, the correlations observed in a particular sample can only be generalized to some extent outside the population on which the model was based.32 For example, odontometric dimensions differ significantly between races; hence, the extent to which a model for determining sex based on data from Caucasians is applicable to other races is limited. It is likely that the model would still show some degree of accuracy, but it would certainly be lower than if the application of the model was limited to the group of subjects on whom the artificial neural network was based. In general, the higher the accuracy of the model, the more homogeneous the group within which it is applied; that is, the less uncontrolled the variance within the group.33 By involving an ever-widening range of different respondents, the heterogeneity of the group increases, and the accuracy of the sex prediction model can be expected to decline. However, if the model is allowed to learn on a sufficiently large sample, it is possible for the neural network to isolate and recognize sex-specific differences despite the large inter-individual variability. In practice, the limitation of the model to a specific population (e.g., race) is not a significant obstacle to successful use, given that several different methods are commonly used in forensics at the same time.34,35 Therefore, there may be several racially specific models for sex determination, each of which works only on a certain subset of respondents, and the choice of the model can be made based on other forensic methods for determining race.36,37 The sample examined in this study was based on study models developed for orthodontic purposes, which means that it was a relatively homogeneous group of young subjects aged 7–18 years. Therefore, the model of an artificial neural network for sex determination does not consider the changes that occur due to tooth wear and restorations, among other age-related factors.38
This study demonstrated the possibility of identifying sexual dimorphism in permanent canines using various statistical methods. It should be noted that model learning in this study was conducted on 121 subjects, which is a relatively small sample size for neural networks that are normally able to process and conduct learning on samples with incomparably larger amounts of data. Although modern forensics have advanced methods that can determine the sex of a subject with almost 100% accuracy,39 these methods are inapplicable in cases where a sufficient amount of hard dental tissue is not available for analysis. In addition, these analyses require expensive equipment and laboratories. If these conditions are not met, simple odontometric methods, such as the neural network model presented in this paper, play an important role in forensic sex determination.40 Further studies with larger and more diverse sample sizes are necessary to confirm these results and improve the accuracy of the model.
In this study, the interdependencies of permanent canine dimensions and anterior Bolton ratio were analyzed, and a model of an artificial neural network that can predict the sex of an unknown respondent with an accuracy of over 80% based on odontometric variables was developed by applying different statistical approaches. This model of sex determination can be applied for forensic purposes, and its accuracy can be further improved by adding data collected from new respondents and/or adding new variables to existing respondents. The improvement in the accuracy of the model was demonstrated through the increase in accurate predictions from 72.0–78.1% to 77.8–85.7% after data on the anterior Bolton ratio and age of the subjects were added to the basic model. The described artificial neural network model for sex determination involves an interdisciplinary approach and combines forensic dentistry and orthodontics to improve the recognition of subjects by expanding the source space of odontometric variables to orthodontic parameters. In addition to the relatively high accuracy given the sample size analyzed in this study, an important feature of the neural network model is its learning ability, that is, the ability to become more accurate with each new subject analyzed by the model. This is an example of machine learning and the foundation of modern computer algorithms for the development of artificial intelligence.
Notes
REFERENCES
1. Dietrichkeit Pereira JG, Lima KF, Alves da Silva RH. 2020; Mandibular measurements for sex and age estimation in Brazilian sampling. Acta Stomatol Croat. 54:294–301. https://doi.org/10.15644/asc54/3/7. DOI: 10.15644/asc54/3/7. PMID: 33132392. PMCID: PMC7586899.

2. Kieser JA. 1990. Human adult odontometrics. Cambridge University Press;Cambridge: https://doi.org/10.1017/CBO9780511983610. DOI: 10.1017/CBO9780511983610. PMCID: PMC258591.

3. Machado V, Botelho J, Mascarenhas P, Mendes JJ, Delgado A. 2020; A systematic review and meta-analysis on Bolton's ratios: normal occlusion and malocclusion. J Orthod. 47:7–29. https://doi.org/10.1177/1465312519886322. DOI: 10.1177/1465312519886322. PMID: 31718451.

4. Capitaneanu C, Willems G, Jacobs R, Fieuws S, Thevissen P. 2017; Sex estimation based on tooth measurements using panoramic radiographs. Int J Legal Med. 131:813–21. https://doi.org/10.1007/s00414-016-1434-0. DOI: 10.1007/s00414-016-1434-0. PMID: 27534562.

5. Moon G, Sathawane R, Chandak R, Lanjekar A, Bhakte K, Sukhdeve V. 2021; Sex determination by odontometric diagonal measurements using discriminant function. J Indian Acad Oral Med Radiol. 33:208–14. https://doi.org/10.4103/jiaomr.jiaomr_260_20. DOI: 10.4103/jiaomr.jiaomr_260_20. PMID: 2a9ada19e9444d0daf4d7fa48f3818d9.

6. Jolliffe IT, Cadima J. 2016; Principal component analysis: a review and recent developments. Philos Trans A Math Phys Eng Sci. 374:20150202. https://doi.org/10.1098/rsta.2015.0202. DOI: 10.1098/rsta.2015.0202. PMID: 26953178. PMCID: PMC4792409.

7. Dreiseitl S, Ohno-Machado L. 2002; Logistic regression and artificial neural network classification models: a methodology review. J Biomed Inform. 35:352–9. https://doi.org/10.1016/s1532-0464(03)00034-0. DOI: 10.1016/S1532-0464(03)00034-0. PMID: 12968784.

8. Gamulin O, Škrabić M, Serec K, Par M, Baković M, Krajačić M, et al. 2021; Possibility of human gender recognition using Raman spectra of teeth. Molecules. 26:3983. https://doi.org/10.3390/molecules26133983. DOI: 10.3390/molecules26133983. PMID: 34210090. PMCID: PMC8271900. PMID: b6d86555e27f4afe8ec569be1f126caf.

9. Shanmuganathan S. Shanmuganathan S, Samarasinghe S, editors. 2016. Artificial neural network modelling: an introduction. Artificial neural network modelling. Springer;Cham: p. 1–14. https://link.springer.com/chapter/10.1007/978-3-319-28495-8_1. DOI: 10.1007/978-3-319-28495-8_1.

10. Bewes J, Low A, Morphett A, Pate FD, Henneberg M. 2019; Artificial intelligence for sex determination of skeletal remains: application of a deep learning artificial neural network to human skulls. J Forensic Leg Med. 62:40–3. https://doi.org/10.1016/j.jflm.2019.01.004. DOI: 10.1016/j.jflm.2019.01.004. PMID: 30639854.

11. Karamizadeh S, Abdullah SM, Manaf AA, Zamani M, Hooman A. 2013; An overview of principal component analysis. J Signal Inf Process. 4:173–5. https://doi.org/10.4236/jsip.2013.43B031. DOI: 10.4236/jsip.2013.43B031.

12. Adams D, Pilloud M. 2019; Sex estimation from dental crown and cervical metrics in a contemporary Japanese sample. Forensic Anthropol. 2:222–32. https://doi.org/10.5744/fa.2019.1008. DOI: 10.5744/fa.2019.1008.

13. Vodanović M, Demo Ž, Njemirovskij V, Keros J, Brkić H. 2007; Odontometrics: a useful method for sex determination in an archaeological skeletal population? J Archaeol Sci. 34:905–13. https://doi.org/10.1016/j.jas.2006.09.004. DOI: 10.1016/j.jas.2006.09.004.

14. Agrawal A, Manjunatha BS, Dholia B, Althomali Y. 2015; Comparison of sexual dimorphism of permanent mandibular canine with mandibular first molar by odontometrics. J Forensic Dent Sci. 7:238–43. https://pubmed.ncbi.nlm.nih.gov/26816466/. DOI: 10.4103/0975-1475.172449. PMID: 26816466. PMCID: PMC4714414.

15. Al Rifaiy MQ, Abdullah MA, Ashraf I. 1997; Dimorphism of mandibular and maxillary canine teeth in establishing sex identity. Saudi Dent J. 9:17–20. https://faculty.ksu.edu.sa/en/malrifaiy/publication/130693.
16. Alam MK, Alzarea BK, Ganji KK, Kundi I, Patil S. 2019; 3D CBCT human adult odontometrics: comparative assessment in Saudi, Jordan and Egypt population. Saudi Dent J. 31:336–42. https://doi.org/10.1016/j.sdentj.2019.03.007. DOI: 10.1016/j.sdentj.2019.03.007. PMID: 31337937. PMCID: PMC6626302.

17. Kuntz TR, Staley RN, Bigelow HF, Kremenak CR, Kohout FJ, Jakobsen JR. 2008; Arch widths in adults with Class I crowded and Class III malocclusions compared with normal occlusions. Angle Orthod. 78:597–603. https://doi.org/10.2319/0003-3219(2008)078[0597:AWIAWC]2.0.CO;2. DOI: 10.2319/0003-3219(2008)078[0597:AWIAWC]2.0.CO;2. PMID: 18302456.

18. Strujić M, Anić-Milosević S, Mestrović S, Slaj M. 2009; Tooth size discrepancy in orthodontic patients among different malocclusion groups. Eur J Orthod. 31:584–9. https://doi.org/10.1093/ejo/cjp013. DOI: 10.1093/ejo/cjp013. PMID: 19339673.

19. Hashim H, Dweik YG, Al-Hussain H. 2018; An odontometric study of arch dimensions among Qatari population sample with different malocclusions. Int J Orthod Rehabili. 9:93–100. https://doi.org/10.4103/ijor.ijor_12_18. DOI: 10.4103/ijor.ijor_12_18.

20. Hashim HA, Al-Sayed N, Al-Hussain H. 2017; Bolton tooth size ratio among Qatari population sample: an odontometric study. J Orthod Sci. 6:22–7. https://doi.org/10.4103/2278-0203.197395. DOI: 10.4103/2278-0203.197395. PMID: 28197399. PMCID: PMC5278581. PMID: 014549fa1e9341c7ab90e8f0cec83cc0.

21. Alshahrani AA, Alshahrani I, Addas MK, Shaik S, Binhomran FM, AlQahtani J. 2020; The tooth size discrepancy among orthodontic patients and normal occlusion individuals from Saudi Arabia: a three-dimensional scan analysis of diagnostic casts. Contemp Clin Dent. 11:141–9. https://doi.org/10.4103/ccd.ccd_455_19. DOI: 10.4103/ccd.ccd_455_19. PMID: 33110327. PMCID: PMC7583543. PMID: 890f1a0968dd436c8b0d28e00b255518.

22. Sravya T, Dumpala RK, Guttikonda VR, Manchikatla PK, Narasimha VC. 2016; Mesiodistal odontometrics as a distinguishing trait: a comparative preliminary study. J Forensic Dent Sci. 8:99–102. https://pubmed.ncbi.nlm.nih.gov/27555727/. DOI: 10.4103/0975-1475.186368. PMID: 27555727. PMCID: PMC4970422.

23. Salam E, Khalifa A, Hassouna D. 2021; Odontometric analysis using CBCT for sexual dimorphism in Egyptian-Fayoum population in case of normal occlusion. Egypt Dent J. 67:1319–32. https://www.researchgate.net/publication/350802113_Odontometric_analysis_using_CBCT_for_sexual_dimorphism_in_Egyptian-Fayoum_population_in_case_of_normal_occlusion. DOI: 10.21608/edj.2021.66478.1542.

24. Gopakumar M, Hegde AM, Janardhanan L. 2013; Gender determination by odontometric parameters-a preliminary study. Indian J Contemp Dent. 1:1–4. https://www.researchgate.net/publication/271350078_Gender_Determination_by_Odontometric_Parameters-A_Preliminary_Study. DOI: 10.5958/j.2320-5962.1.1.001.

25. Sharma S, Sharma S, Athaiya A. 2020; Activation functions in neural networks. Int J Eng Appl Sci Technol. 4:310–6. https://doi.org/10.33564/IJEAST.2020.v04i12.054. DOI: 10.33564/IJEAST.2020.v04i12.054.

26. Obuchowski NA, Bullen JA. 2018; Receiver operating characteristic (ROC) curves: review of methods with applications in diagnostic medicine. Phys Med Biol. 63:07TR01. https://doi.org/10.1088/1361-6560/aab4b1. DOI: 10.1088/1361-6560/aab4b1. PMID: 29512515.

27. Centor RM. 1991; Signal detectability: the use of ROC curves and their analyses. Med Decis Making. 11:102–6. https://doi.org/10.1177/0272989X9101100205. DOI: 10.1177/0272989X9101100205. PMID: 1865776.

28. Murray PE, Stanley HR, Matthews JB, Sloan AJ, Smith AJ. 2002; Age-related odontometric changes of human teeth. Oral Surg Oral Med Oral Pathol Oral Radiol Endod. 93:474–82. https://doi.org/10.1067/moe.2002.120974. DOI: 10.1067/moe.2002.120974. PMID: 12029288.

29. Khamis MF, Taylor JA, Malik SN, Townsend GC. 2014; Odontometric sex variation in Malaysians with application to sex prediction. Forensic Sci Int. 234:183.e1–7. https://doi.org/10.1016/j.forsciint.2013.09.019. DOI: 10.1016/j.forsciint.2013.09.019. PMID: 24128748.

30. Narang RS, Manchanda AS, Singh B. 2015; Sex assessment by molar odontometrics in North Indian population. J Forensic Dent Sci. 7:54–8. https://pubmed.ncbi.nlm.nih.gov/25709321/. DOI: 10.4103/0975-1475.150318. PMID: 25709321. PMCID: PMC4330620.

31. Viciano J, Alemán I, D'Anastasio R, Capasso L, Botella MC. 2011; Odontometric sex discrimination in the Herculaneum sample (79 AD, Naples, Italy), with application to juveniles. Am J Phys Anthropol. 145:97–106. https://doi.org/10.1002/ajpa.21471. DOI: 10.1002/ajpa.21471. PMID: 21312179.

32. Grewal DS, Khangura RK, Sircar K, Tyagi KK, Kaur G, David S. 2017; Morphometric analysis of odontometric parameters for gender determination. J Clin Diagn Res. 11:ZC09–13. https://doi.org/10.7860/JCDR/2017/26680.10341. DOI: 10.7860/JCDR/2017/26680.10341. PMID: 28969265. PMCID: PMC5620906. PMID: 9ff9f9c4b4de4e61b9581de265267f6f.

33. Sawyer SF. 2009; Analysis of variance: the fundamental concepts. J Man Manip Ther. 17:27E–38E. https://doi.org/10.1179/jmt.2009.17.2.27E. DOI: 10.1179/jmt.2009.17.2.27E.

34. Adserias-Garriga J, Thomas C, Ubelaker DH, C Zapico S. 2018; When forensic odontology met biochemistry: multidisciplinary approach in forensic human identification. Arch Oral Biol. 87:7–14. https://doi.org/10.1016/j.archoralbio.2017.12.001. DOI: 10.1016/j.archoralbio.2017.12.001. PMID: 29241027.

35. Pretty IA, Sweet D. 2001; A look at forensic dentistry--part 1: the role of teeth in the determination of human identity. Br Dent J. 190:359–66. https://doi.org/10.1038/sj.bdj.4800972. DOI: 10.1038/sj.bdj.4800972. PMID: 11338039.

36. Senn DR, Stimson PG. 2010. Forensic dentistry. 2nd ed. CRC Press;Boca Raton: p. 437. https://www.routledge.com/Forensic-Dentistry/Senn-Stimson/p/book/9781420078367. DOI: 10.4324/9780429292767.
37. Senn DR, Weems RA. 2013. Manual of forensic odontology. 5th ed. Taylor & Francis;Boca Raton: p. 445. https://www.routledge.com/Manual-of-Forensic-Odontology/Senn-Weems/p/book/9780367778514. DOI: 10.1201/b13744.
38. Nagaratnam N, Nagaratnam K, Cheuk G. Nagaratnam N, Nagaratnam K, Cheuk G, editors. 2017. Oral issues in the elderly. Geriatric diseases. Springer;Cham: p. 1–8. https://link.springer.com/referenceworkentry/10.1007/978-3-319-32700-6_92-1. DOI: 10.1007/978-3-319-32700-6_92-1.

39. Rai B, Kaur J. 2012. Evidence-based forensic dentistry. Springer International Publishing;New York: https://link.springer.com/book/10.1007/978-3-642-28994-1.
40. Franklin D. 2010; Forensic age estimation in human skeletal remains: current concepts and future directions. Leg Med (Tokyo). 12:1–7. https://doi.org/10.1016/j.legalmed.2009.09.001. DOI: 10.1016/j.legalmed.2009.09.001. PMID: 19853490.

Figure 2
Odontometric variables in the rotated space of the first two main components for the principal component analysis model for both sexes.
CI, cervical-incisal; MD, mesiodistal; VO, vestibular-oral.
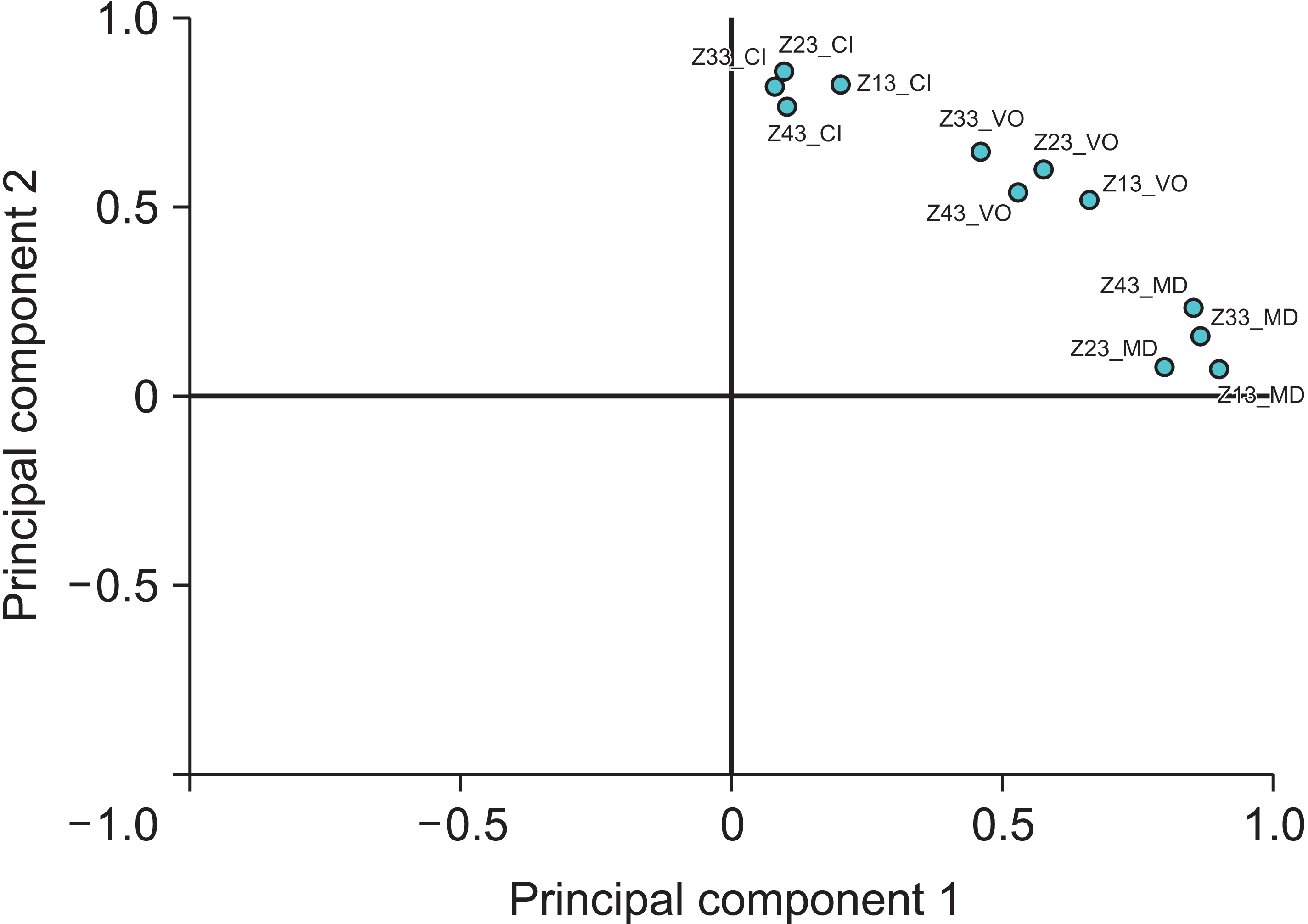
Figure 4
Representation of odontometric variables in the rotated space of the first two main components of the principal component analysis model for male participants.
CI, cervical-incisal; MD, mesiodistal; VO, vestibular-oral.
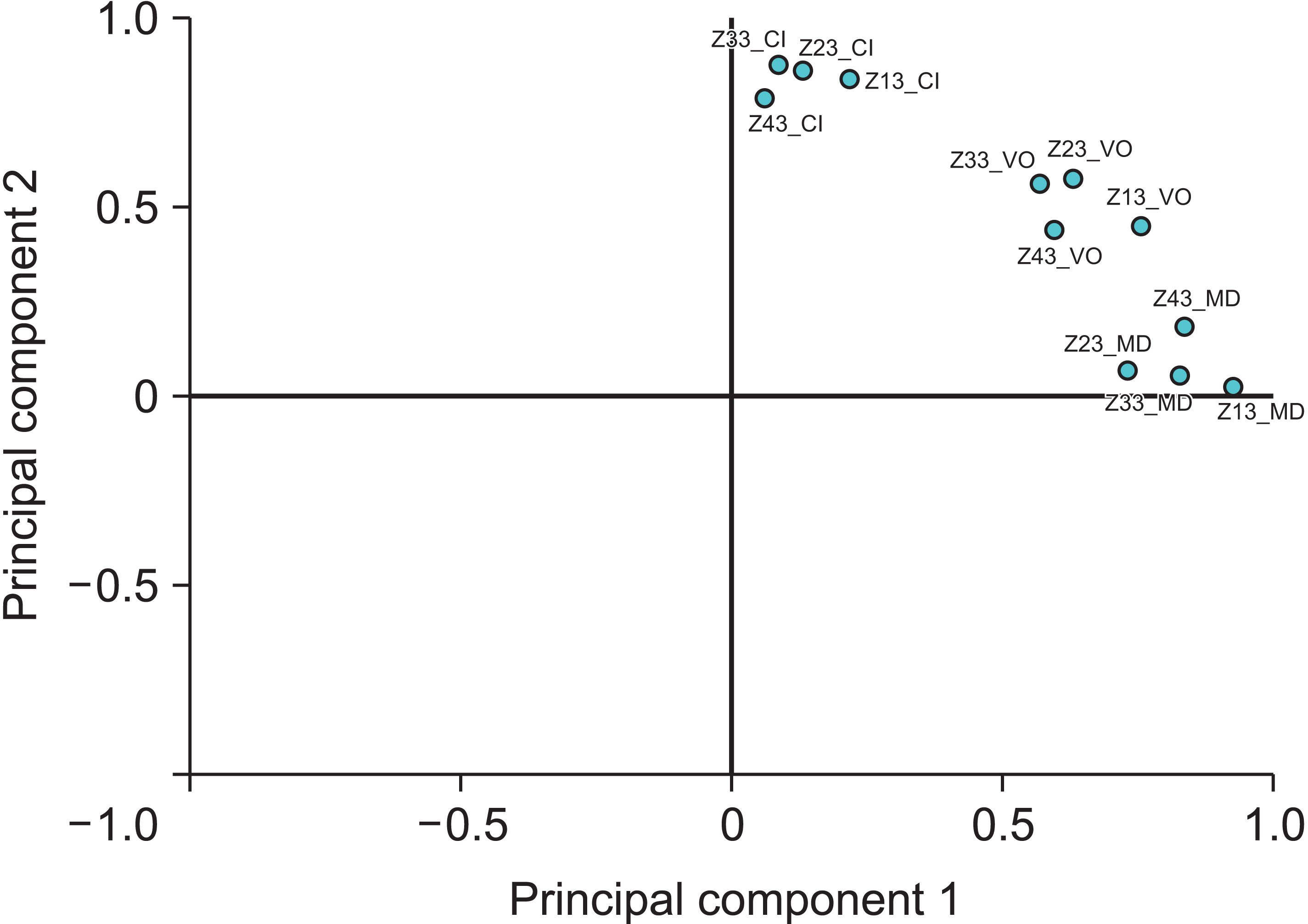
Figure 6
Representation of odontometric variables in the rotated space of the first two main components of the principal component analysis model for female participants.
CI, cervical-incisal; MD, mesiodistal; VO, vestibular-oral.
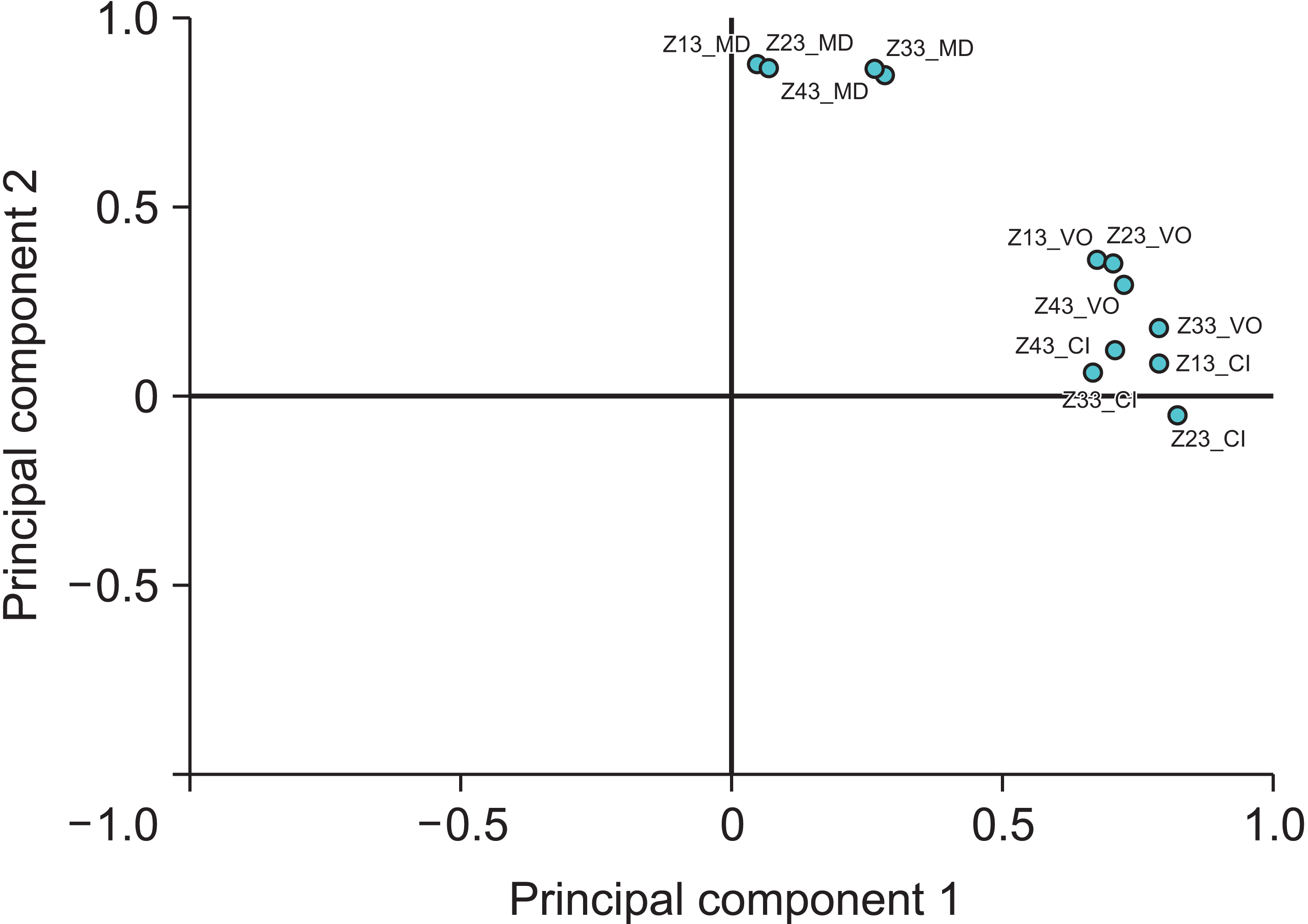
Figure 7
Odontometric variables and the anterior Bolton ratio in the rotated space of the first three main components of the principal component analysis models for participants of A, both sexes, B, male, and C, female participants.
CI, cervical-incisal; MD, mesiodistal; VO, vestibular-oral.
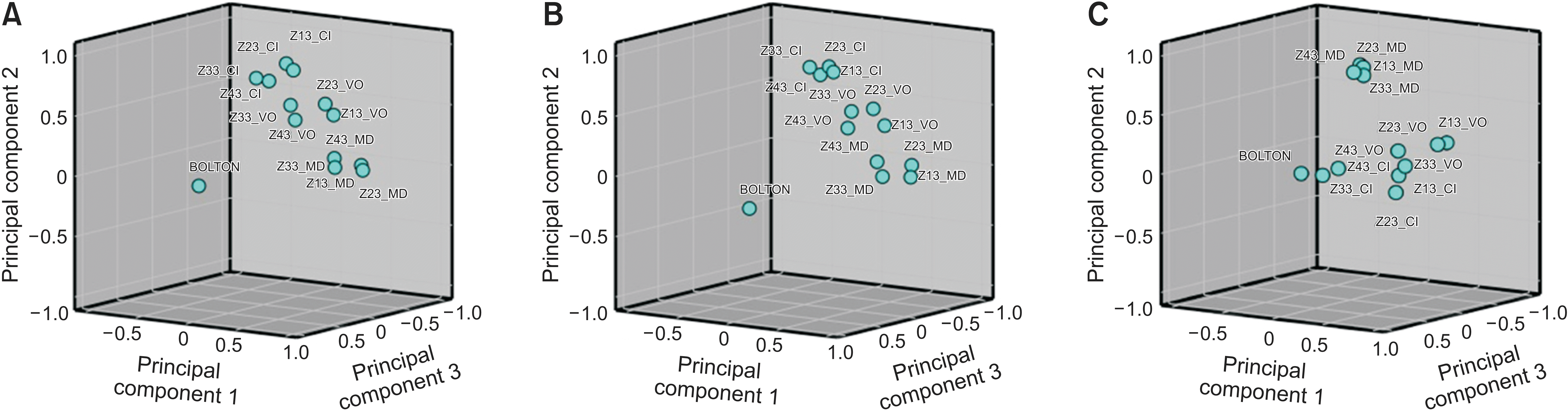
Figure 8
Scattering diagram of the values of the first two main components. One dot indicates one respondent.
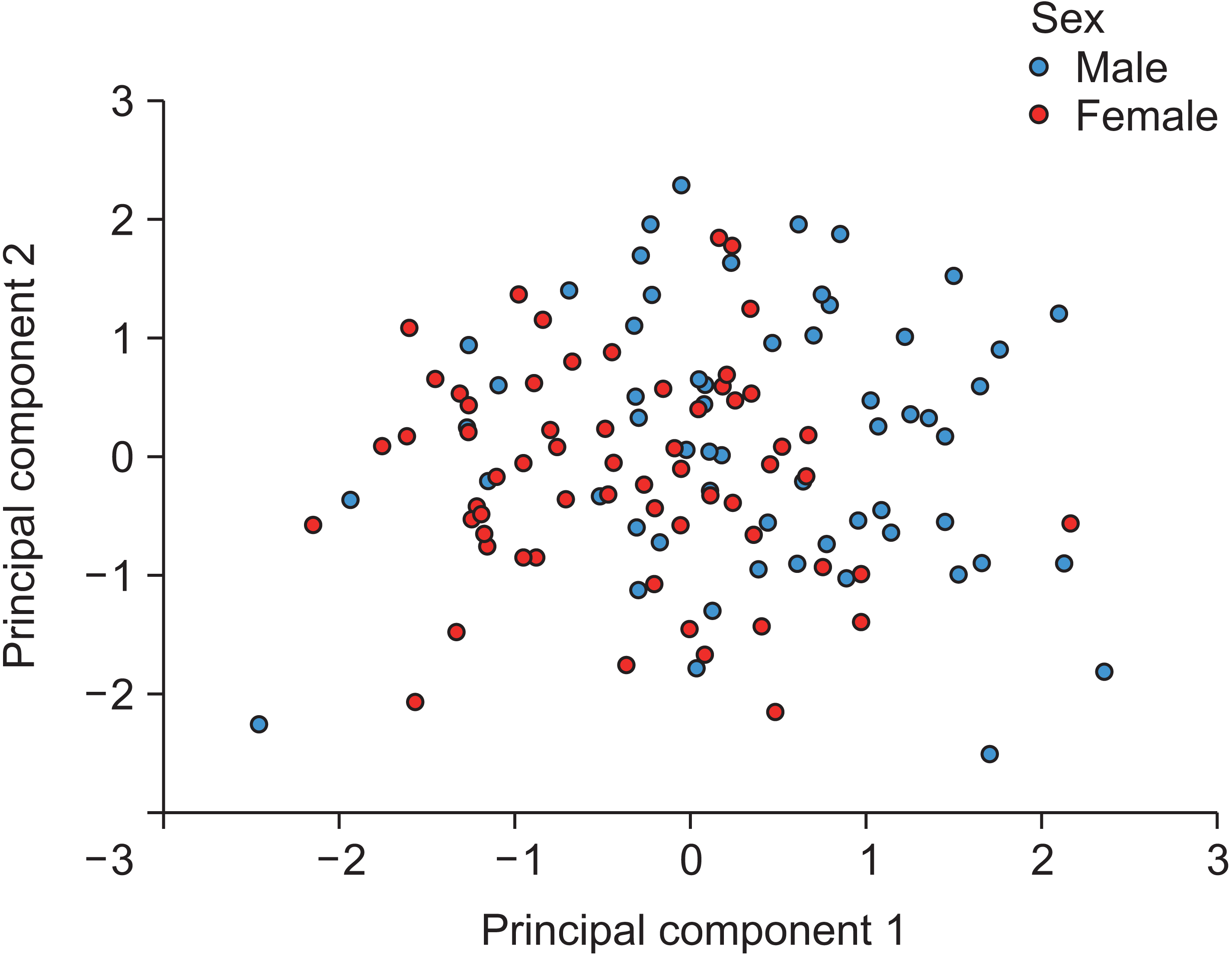
Figure 9
Scattering diagram of the values of the first three main components of the principal component analysis model that included odontometric variables and the anterior Bolton ratio. One dot indicates one respondent.
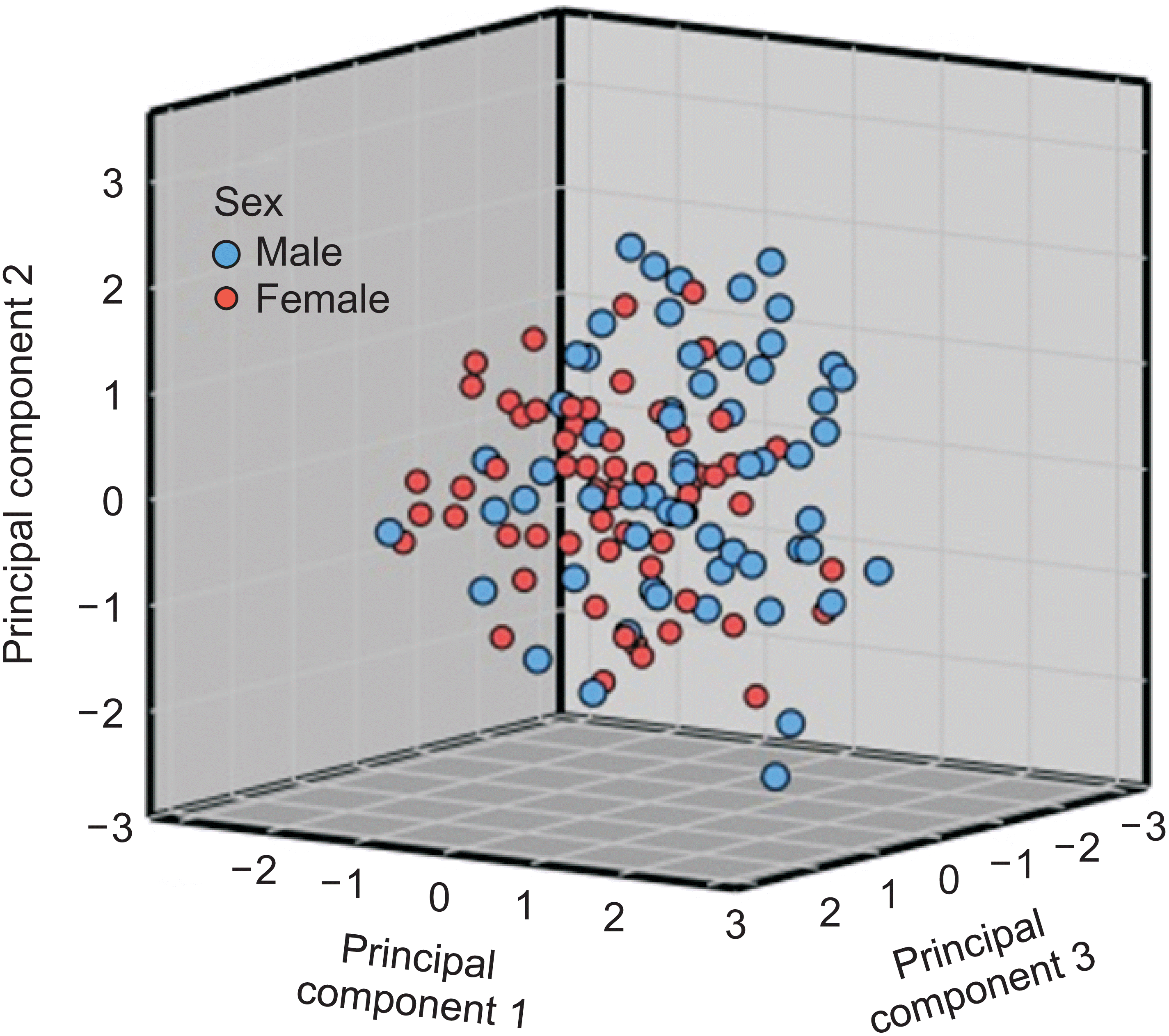
Figure 10
A, Schematic illustration of the optimized neural network and B, the corresponding operational characteristics curve.
CI, cervical-incisal; MD, mesiodistal; VO, vestibular-oral; M, male; F, female.

Table 1
Odontometric variables and comparison between sexes




 PDF
PDF Citation
Citation Print
Print



 XML Download
XML Download