I. Introduction
Hemorrhage is a serious clinical event that can result in organ failure, coma, and death. Massive bleeding requires blood transfusion, causes low perfusion-related damage to major tissues and organs, and increases morbidity and mortality [
1–
3]. Specifically, patients who bleed severely in intensive care units (ICUs) are often at an elevated risk of mortality and extended hospital stay [
4]. In many cases, hemorrhage causes loss of blood volume, and patients with potentially fatal bleeding are a critical issue for both medical teams and blood banks [
5]. Blood supplies could be delayed in life-threatening situations for various reasons, and such delays during emergencies could have irreversible adverse outcomes for patients. Therefore, it is essential to promptly recognize and treat bleeding to avoid adverse outcomes and complications. The early prediction of hemorrhage in the ICU could improve patient safety by ensuring sufficient blood management. Furthermore, since it is expensive to store unnecessarily large amounts of blood, the ability to predict hemorrhage might help in properly maintaining the blood supply chain, thereby reducing costs [
6].
Electronic medical record systems have recently been established at many hospitals. These systems facilitate the management and secondary analyses of big clinical data generated in hospitals [
7]. Patients with the most severe conditions are admitted to the ICU, which uses more medical resources and equipment than general wards and generates large amounts of data [
8]. Machine learning, which is a branch of artificial intelligence, is instrumental in healthcare because it can be used to generate and interpret information faster than an individual medical professional. The ICU is an optimal environment for applying machine learning techniques in clinical decision-making [
9,
10].
Several studies have attempted to identify patient variables and biomarkers associated with bleeding, but no clear single factor or predictor has been identified that can predict hemorrhage in individual patients [
11]. Hemoglobin, hematocrit, systolic blood pressure, and heart rate are known to be closely correlated with hypovolemia, and several studies have reported clinically significant parameters for the early recognition of the occurrence of bleeding [
12–
14]. Coagulation tests are also used to diagnose problems in the hemostatic system and can help assess the risk of excessive bleeding or thrombosis. Before surgery, coagulation tests are recommended to predict potential bleeding and blood clotting disorders [
15,
16]. The blood urea nitrogen test is used to measure the amount of urea nitrogen in the blood, which represents a waste product of protein metabolism [
17,
18]. The excessive accumulation of nitrogen-containing compounds, such as uric acid and creatinine, in the blood is associated with gastrointestinal bleeding [
19]. Additionally, some studies have identified age, sex, cardiovascular disease, and kidney disease as risk factors for bleeding [
11]. There are several complex predictors of bleeding, and it is necessary to integrate various factors to predict bleeding.
Several studies have been conducted on the early detection of bleeding among patients in ICUs. However, most of those studies mainly focused on patients experiencing gastrointestinal bleeding or bleeding as a complication following specific surgical procedures [
20–
22]. In this study, we attempted to consider all types of bleeding requiring emergency blood transfusion in the ICU setting.
We aimed to develop a machine learning model for predicting hemorrhage. Our proposed model learns the patterns of continuously changing real-world clinical data. We expected to identify groups at a high risk of hemorrhage during ICU admission in a manner that would allow pre-emptive interventions.
II. Methods
1. Data Source
In this retrospective study, we used data obtained from the Medical Information Mart for Intensive Care (MIMIC) databases. The MIMIC databases are sizeable, freely available databases comprising de-identified health-related data of patients admitted to the ICU at the Beth Israel Deacons Medical Center, which is a tertiary medical institution located in Boston, USA. The data include demographics, vital signs, laboratory results, prescriptions, and notes, among other data concerning critical patients [
23]. We analyzed the most recent versions of the MIMIC databases: MIMIC-III v1.4 and MIMIC-IV v1.0. The MIMIC-III clinical database contains data obtained between 2001 and 2012. The data were collected using MetaVision (iMDSoft, Wakefield, MA, USA) and CareVue (Philips Healthcare, Cambridge, MA, USA) systems. The original Philips CareVue system (archived data from 2001 to 2008) was replaced with the new MetaVision data management system, which continues to be used today. The MIMIC-IV database contains data obtained between 2008 and 2019. The data were collected using the MetaVision system. We used CareVue data obtained from the MIMIC-III database (2001–2008) as the training dataset, except for the overlapping collection period, and we used data from the MIMIC-IV database (2008–2019) as the internal test dataset.
2. Ethics and Data Use Agreement
We completed the online human research ethics training required by PhysioNet Clinical Databases and were granted access to the data according to the procedures presented. The Ajou University Hospital Institutional Review Board approved the study protocol (No. AJIRB-MED-EXP-21-526).
3. Definition of the Outcome of Interest
We studied patients aged 18 years and above who were admitted to the ICU, as recorded in the MIMIC databases. Hemorrhage was defined as follows. First, we considered hemorrhage as occurring in patients who received transfusions of more than 1 unit of packed red blood cells (PRBCs) after admission to the ICU, based on 53 International Classification of Diseases (ICD) procedure codes (ICD-9 and ICD-10), including “control of hemorrhage” or “control of bleeding” (
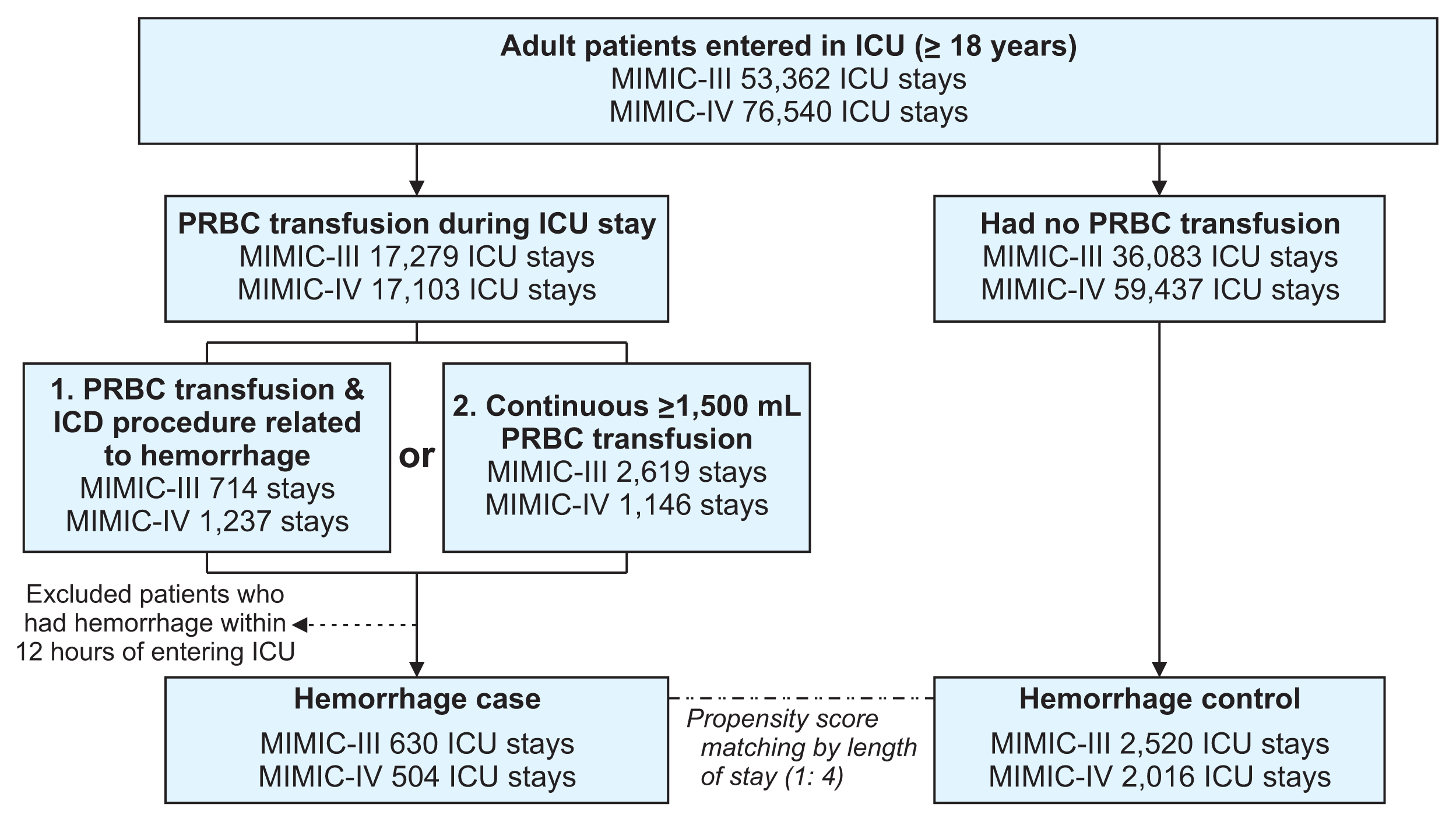
Supplementary Table S1). Second, we defined hemorrhage as occurring in patients who were continuously transfused with more than 1,500 mL of PRBCs within 3 hours after the start of transfusion. Among the patients satisfying either condition, we excluded those who experienced hemorrhage within 12 hours of ICU admission owing to insufficient input length. As the control group, we selected patients who did not receive blood transfusions during their stay in the ICU. Controls were matched to cases based on the length of stay at a ratio of 1:4 using propensity score-matching. Finally, we labeled the data as hemorrhage cases (n = 1,134) or controls (n = 4,536). A flowchart of the patient selection process is presented in
Figure 1.
Figure 1
Flowchart of the patient selection process. A detailed flow chart of the patient selection process by dataset. We selected 5,670 intensive care admissions including hemorrhage cases (n = 1,134) and hemorrhage controls (n = 4,536). MIMIC: Medical Information Mart for Intensive Care, ICU: intensive care unit, PRBC: packed red blood cells.

4. Input Variables
We extracted the patient information that provided the most relevant clinical features on ICU stays from the databases. The candidate features comprised static and dynamic feature information. Patient information included patient status, vital signs, the Glasgow Coma Scale (GCS) score, complete blood count (CBC), chemistry measurements, coagulation measurements, and urine output. Patient status included four features: age, sex, weight, and the Elixhauser comorbidity index. The vital signs included seven features: systolic, mean, and diastolic blood pressure, heart rate, respiratory rate, body temperature, and oxygen saturation (SpO
2). The GCS included three features: GCS eye, GCS verbal, and GCS motor. The CBC included four features: hematocrit, hemoglobin, white blood cells, and platelet count. The chemistry measurements included five features: potassium, sodium, blood urea nitrogen, creatinine, and glucose levels. The coagulation measurements included three features: partial thromboplastin time, international normalized ratio, and prothrombin time. Urine output was a single feature. We developed three machine models that included increasingly larger amounts of information (i.e., higher numbers of input features) and evaluated their performance. Model 1 was developed based only on patient status (four features) and vital signs (seven features). Model 2 used additional input information from the GCS (three features) and CBC (four features), along with the input for model 1. Model 3 used additional input information on chemistry (five features), coagulation (three features), and urine output (one feature) along with the input from model 2. The input features used for each of the three models are summarized in
Table 1.
Table 1
|
Category |
Features |
|
11 features for Model 1 |
|
Patient status (4 features) |
Age, gender, weight, Elixhauser comorbidity score |
|
Vital signs (7 features) |
Systolic, mean, and diastolic blood pressure, heart rate, respiratory rate, body temperature, SpO2
|
|
|
Additional 7 features for Model 2 (total of 18 features) |
|
GCS (3 features) |
GCS eye, GCS verbal, GCS motor |
|
CBC (4 features) |
Hematocrit, hemoglobin, WBC, platelet count |
|
|
Additional 9 features for Model 3 (total of 27 features) |
|
Chemistry (5 features) |
Potassium, sodium, BUN, creatinine, glucose |
|
Coagulation (3 features) |
PTT, INR, PT |
|
Output value (1 feature) |
Urine output |

5. Data Preprocessing
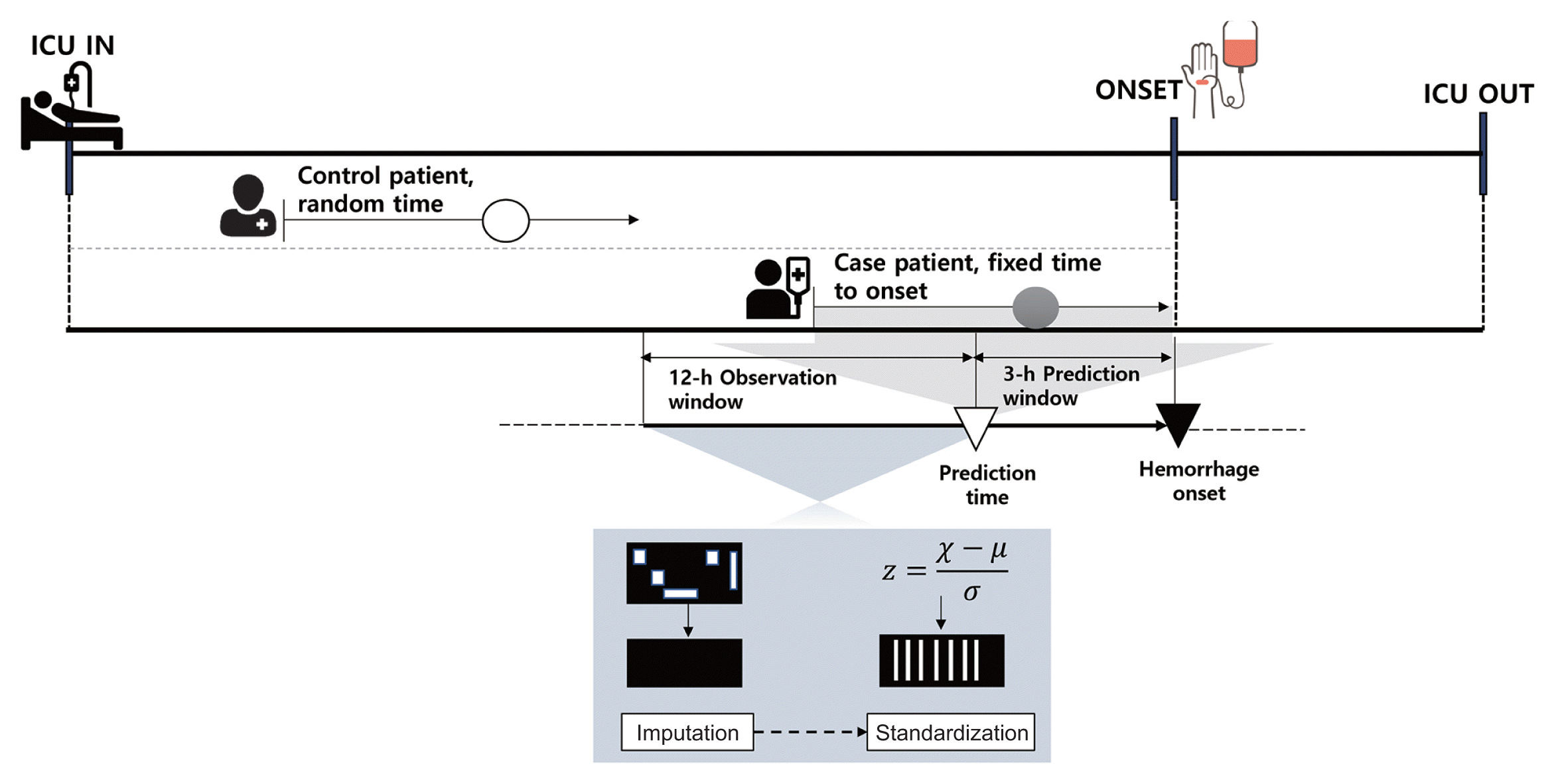
For time-varying features, such as vital signs, we considered a 12-hour observation window before the time at which hemorrhage was predicted. The average time interval for all feature measurements within the observation window was 32 minutes for the MIMIC-III dataset and 22 minutes for the MIMIC-IV dataset. Considering the average intervals and those that can be used to divide the 12-hour observation window into the same sequence, a 30-minute interval sequence of all the features was used as the input for our proposed model. For static features, we replicated the values for each input window. Logically contradictory outliers were removed, and extreme values above the 99th percentile were replaced with values in the 99th percentile. The continuous features were then normalized to z-scores by subtracting the mean and scaling each feature into unit variance. Missing values within the observation window were replaced by linear interpolation, and the data at each point in time were sorted sequentially. The overall architecture of data preprocessing is illustrated in
Figure 2.
Figure 2
Overall architecture of data preprocessing. For patients with hemorrhage, prediction results were obtained 3 hours prior to the point of onset during the period of ICU stays, and patient data for the previous 12 hours were used as input. Control patients’ input data were extracted at random times during ICU stays. All input data were preprocessed through missing-data imputation and a standardization process. ICU: intensive care unit.

6. Model Development
In this study, to predict hemorrhage in the ICU, we used the gated recurrent unit (GRU) model, which is a modified structure of a recurrent neural network (RNN) for solving the vanishing or exploding gradient problem [
24]. The GRU model is used widely for time series forecasting along with a long short-term memory network [
25]. The model was designed to present predictive results for hemorrhage 3 hours before it occurs. We first designed the GRU layers, followed by sigmoid activation. We performed hyperparameter tuning for the three models. Subsequently, we found that the optimal architecture was five-layer GRUs with 20 hidden layers and Xavier initialization, followed by sigmoid activation for the three models.
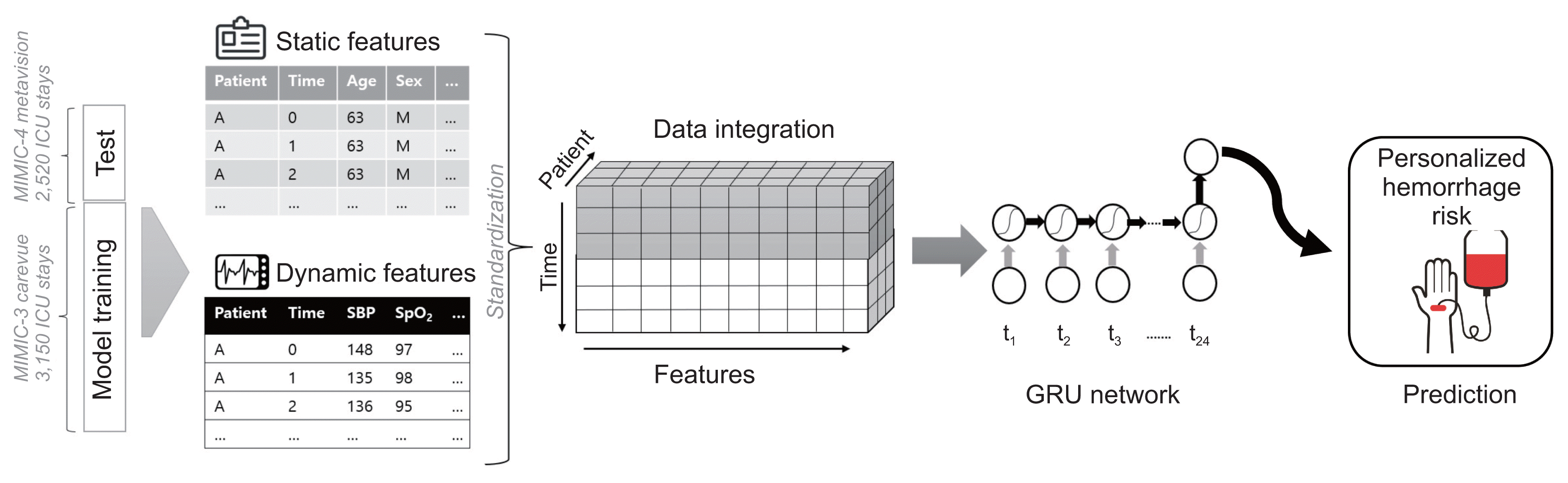
Figure 3 shows an architectural overview of our hemorrhage prediction models. We used a binary cross-entropy loss of over 300 training epochs using the Adam optimizer, with a learning rate of 0.001. Hyperparameter tuning was performed empirically.
Figure 3
Architectural overview of the hemorrhage prediction model. Dynamic features are extracted as time series, whereas static features are replicated over time. These values are integrated as a matrix of all features and labels for each patient. At each time step, the model receives current slice data as input, and features are captured in a truly sequential structure. GRU: gated recurrent unit.

7. Performance Evaluation
The hemorrhage prediction model was trained using the MIMIC-III dataset and evaluated using the MIMIC-IV dataset. The performance of the model was assessed by comparing the actual label with the label predicted using the model. True positives represent correctly classified samples belonging to a specific class. True negatives correspond to samples that do not belong to a specific class and are classified as not belonging to the class. False positives represent the samples that do not belong to a specific class but are classified as belonging to the class. False negatives are misclassified samples belonging to a specific class. We evaluated the predictive performance of our proposed model using general performance metrics: positive predictive value, negative predictive value, sensitivity, specificity, and area under the receiver operating characteristic (AUROC) curve. We also included the F1-score to compute the harmonic mean of the two scores and reflect the trade-off between precision and sensitivity. The AUROC curve has a range of between 0.5 and 1; the closer it is to 1, the better the performance. The area under the precision-recall curve (AUPRC) is the area under the curve drawn with the x-axis as the recall and the y-axis as the precision, and it is useful when there is an imbalance between labels.
8. External Validation
The eICU Collaborative Research Database (eICU) was used for external verification of model 3, which demonstrated the best performance. The eICU is an open database created through collaboration with Philips Healthcare in the United States and the MIT Laboratory for Computational Physics [
26]. It comprises data collected from ICUs at more than 300 hospitals across the United States and covers patients admitted between 2014 and 2015. The eICU database does not contain information regarding the ICD procedures. Therefore, only patients who had a continuous transfusion of more than 1,500 mL of PRBC were defined as having hemorrhage, corresponding to the second condition of the outcome definition. Additionally, the data obtained from the eICU showed a lower time resolution of laboratory test results and more missing values than the data from the MIMIC database. All input features were limited to patients with values measured more than once. The measured features were used to process the 30-minute interval sequence similar to the main model. Missing values were imputed based on the patient’s last measurement. Therefore, each time step represented a recent measurement. This is the most realistic approach because doctors also observe the last measurement when evaluating a patient’s status. Forty-four patients were selected as hemorrhage cases, and 176 controls were selected through the same propensity score-matching process.
For patient selection, data preprocessing, group matching, and the imputationentry of missing values, we used Microsoft SQL server (MSSQL; v15.0, R v4.0.3) with the tidyverse (v1.3.1), comorbidity (v0.5.3), MatchIt (v4.2.0), ggplot2 (v3.3.4), and Python v3.8.5 packages, and with the pyodbc (v4.0.0), pandas (v1.1.3), scipy (v1.5.2), and numpy (v1.19.2) modules. For model development, we used Python v3.8.5 with the sklearn (v0.24.1), pytorch (v1.9.1), matplotlib (v3.3.2), pandas (v1.1.3), and numpy (v1.19.2) modules. The model was trained using an NVIDIA GeForce RTX 2080 Ti graphics processing unit (GPU).
III. Results
The complete training set from the MIMIC-III database comprised 3,150 ICU stays, corresponding to 2,996 patients, and the test set from the MIMIC-IV database included 2,520 ICU stays, corresponding to 2,440 patients. The general characteristics of the patients are expressed as numbers (%) or as mean ± standard deviation. For each numeric characteristic, the
t-test was performed to compare the hemorrhage cases with the control group. The chi-square test was used to evaluate categorical characteristics. Differences were considered statistically significant if the
p-value was less than 0.05 (
Table 2).
Table 2
Baseline characteristics in the training and test sets
|
MIMIC-III |
MIMIC-IV |
|
|
|
Hemorrhage case |
Control |
p-value |
Hemorrhage case |
Control |
p-value |
|
Number of ICU admissions |
630 |
2,520 |
|
504 |
2,016 |
|
|
|
Number of patients |
618 |
2,378 |
|
475 |
1,965 |
|
|
|
Age (yr) |
63.0 ± 16.1 |
63.1 ± 17.0 |
0.90 |
63.4 ± 16.0 |
62.8 ± 16.5 |
0.47 |
|
|
Sex |
|
Male |
395 (62.7) |
1,476 (58.6) |
0.47 |
320 (63.5) |
1,203 (59.7) |
0.65 |
|
Female |
235 (37.3) |
1,044 (41.4) |
|
184 (36.5) |
813 (40.3) |
|
|
|
Care unit |
|
MICU |
278 (44.1) |
1,042 (41.3) |
<0.001 |
109 (21.6) |
410 (20.3) |
<0.001 |
|
SICU |
78 (12.4) |
506 (20.1) |
|
110 (21.8) |
409 (20.3) |
|
|
CCU |
127 (20.2) |
389 (15.4) |
|
50 (9.9) |
237 (11.8) |
|
|
TSICU |
59 (9.4) |
343 (13.6) |
|
55 (10.9) |
276 (13.7) |
|
|
CSRU |
88 (14.0) |
240 (9.5) |
|
- |
- |
|
|
MICU/SICU |
- |
- |
|
66 (13.1) |
312 (15.5) |
|
|
CVICU |
- |
- |
|
104 (20.6) |
174 (8.6) |
|
|
NSICU |
- |
- |
|
10 (2.0) |
198 (9.8) |
|
|
|
Length of stay (day) |
19.6 ± 18.9 |
8.5 ± 5.6 |
<0.001 |
14.3 ± 16.4 |
10.9 ± 9.0 |
<0.001 |

Table 3 shows the distribution of the mean and standard deviation of the input features for each model. The mean value of the Elixhauser comorbidity index was higher in the hemorrhage group than in the control group. Patients in the hemorrhage group tended to have high initial severity. In the MIMIC-III dataset, the mean blood pressure in the hemorrhage group was lower, and the heart and respiratory rates were faster, but this trend was not consistent in the MIMIC-IV dataset. Hemoglobin, hematocrit, platelets, and complete blood count indicators had lower mean values in the hemorrhage group than in the control group in all datasets, and the difference was statistically significant. The measured mean differences of 18 variables in the MIMIC-III dataset and 20 variables in the MIMIC-IV dataset were statistically significant.
Table 3
Statistics of input features for all three models in the training and test sets
|
MIMIC-III |
MIMIC-IV |
|
|
|
Hemorrhage case |
Control |
p-value |
Hemorrhage case |
Control |
p-value |
|
Model 1 |
|
Elixhauser comorbidity |
14.2 ± 11.0 |
11.9 ± 11.0 |
<0.001 |
21.4 ± 13.1 |
17.9 ± 12.3 |
<0.001 |
|
Weight |
83.2 ± 24.1 |
83.0 ± 25.0 |
0.86 |
84.1 ± 24.2 |
87.4 ± 34.6 |
0.04 |
|
Systolic BP |
113.7 ± 22.1 |
126.5 ± 30.3 |
<0.001 |
117.8 ± 31.2 |
144.6 ± 49.7 |
<0.001 |
|
Diastolic BP |
55.6 ±14.6 |
63.6 ± 17.2 |
<0.001 |
62.1 ± 15.5 |
75.8 ± 18.2 |
<0.001 |
|
Mean BP |
74.2 ± 14.9 |
84.0 ± 23.2 |
<0.001 |
77.7 ± 25.0 |
102.8 ± 44.3 |
<0.001 |
|
Heart rate |
91.9 ± 19.8 |
90.8 ± 21.1 |
0.25 |
88.3 ± 17.7 |
90.4 ± 23.1 |
0.05 |
|
Respiratory rate |
19.8 ± 6.2 |
19.1 ± 7.0 |
0.03 |
19.7 ± 6.0 |
20.2 ± 6.7 |
0.13 |
|
Temperature |
37.0 ± 1.0 |
36.7 ± 1.1 |
<0.001 |
36.9 ± 0.8 |
36.9 ± 1.0 |
0.09 |
|
SpO2
|
97.0 ± 4.7 |
96.9 ± 5.2 |
0.70 |
97.5 ± 2.7 |
96.7 ± 4.3 |
<0.001 |
|
|
Model 2 |
|
GCS eye |
2.9 ± 1.2 |
2.8 ± 1.3 |
0.12 |
2.9 ± 1.2 |
2.8 ± 1.3 |
0.03 |
|
GCS verbal |
2.5 ± 1.8 |
2.8 ± 1.9 |
<0.001 |
2.9 ± 1.9 |
2.8 ± 1.9 |
0.35 |
|
GCS motor |
4.8 ± 1.7 |
4.7 ± 1.9 |
0.23 |
4.7 ± 1.9 |
4.7 ± 1.9 |
0.94 |
|
Hematocrit |
27.8 ± 4.2 |
34.8 ± 5.8 |
<0.001 |
26.7 ± 4.6 |
37.9 ± 8.1 |
<0.001 |
|
Hemoglobin |
9.3 ± 1.4 |
11.7 ± 2.0 |
<0.001 |
8.9 ± 1.7 |
13.2 ± 3.8 |
<0.001 |
|
WBC |
13.2 ± 7.6 |
13.3 ± 8.6 |
0.74 |
14.2 ± 9.1 |
29.8 ± 34.9 |
<0.001 |
|
Platelets |
206.3 ± 132.5 |
240.3 ± 123.4 |
<0.001 |
180.9 ± 117.6 |
386.3 ± 320.0 |
<0.001 |
|
|
Model 3 |
|
Potassium |
4.1 ± 0.6 |
4.1 ± 0.7 |
0.84 |
4.2 ± 0.7 |
4.9 ± 2.0 |
<0.001 |
|
Sodium |
138.5 ± 4.4 |
139.0 ± 4.5 |
0.02 |
138.8 ± 5.6 |
148.9 ± 23.3 |
<0.001 |
|
BUN |
35.6 ± 26.6 |
63.6 ± 73.2 |
<0.001 |
37.9 ± 30.2 |
50.5 ± 64.2 |
<0.001 |
|
Creatinine |
1.8 ± 1.5 |
3.2 ± 3.7 |
<0.001 |
1.8 ± 1.6 |
2.6 ± 3.3 |
<0.001 |
|
Glucose |
142.2 ± 57.5 |
147.5 ± 57.4 |
0.04 |
141.5 ± 51.5 |
171.1 ± 76.8 |
<0.001 |
|
PTT |
46.0 ± 26.7 |
38.6 ± 21.7 |
<0.001 |
45.0 ± 21.8 |
54.9 ± 33.0 |
<0.001 |
|
PT |
16.3 ± 7.5 |
20.1 ± 20.0 |
<0.001 |
19.1 ± 12.7 |
41.2 ± 39.2 |
<0.001 |
|
INR |
1.7 ± 1.2 |
2.0 ± 2.1 |
<0.001 |
1.8 ± 1.3 |
4.0 ± 4.0 |
<0.001 |
|
Urine output |
119.8 ± 145.9 |
286.6 ± 294.5 |
<0.001 |
154.7 ± 209.0 |
296.2 ± 323.6 |
<0.001 |

The performance of each model with the internal test set is presented in
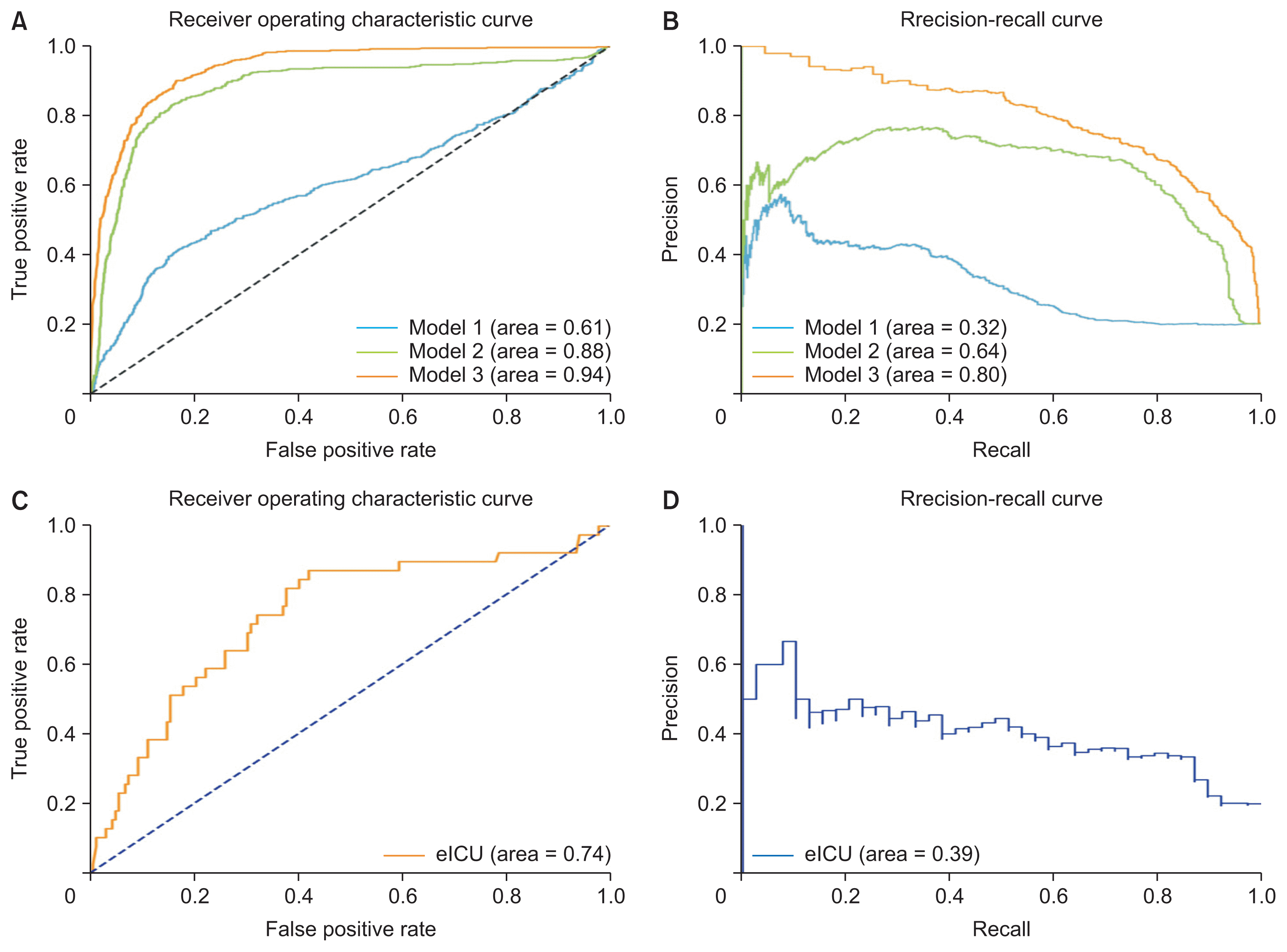
Table 4. Model 1 used 11 input variables, including only the patient’s basic information and vital signs, and it showed an accuracy of 0.76, a sensitivity of 0.39, a specificity of 0.85, and an AUROC of 0.61. Model 2, which used a total of 18 input variables with the addition of GCS and CBC, showed improved performance compared to model 1, with an accuracy of 0.87, sensitivity of 0.75, specificity of 0.90, and an AUROC of 0.88. Using the final 27 input variables, including blood coagulation tests, electrolytes, other blood chemistry tests, and urine output, model 3 achieved an accuracy of 0.88, a sensitivity of 0.81, a specificity of 0.90, and an AUROC of 0.94.
Table 4
Predictive model performance in the MIMIC-IV test set
|
Accuracy |
PPV |
NPV |
Sensitivity |
Specificity |
F1-score |
AUROC |
AUPRC |
|
Model 1 |
0.76 |
0.39 |
0.85 |
0.39 |
0.85 |
0.39 |
0.61 |
0.32 |
|
Model 2 |
0.87 |
0.66 |
0.94 |
0.75 |
0.90 |
0.70 |
0.88 |
0.64 |
|
Model 3 |
0.88 |
0.67 |
0.95 |
0.81 |
0.90 |
0.73 |
0.94 |
0.80 |

Figure 4 shows the AUROC and AUPRC curves for each model in which the number of input features was increased step by step. The AUROC and AUPRC values from model 2 were higher than those from model 1. The AUROC and AUPRC values from model 3 were higher than those from model 2. Model 3, which used data for all the input variables, showed the highest performance. These findings indicate that hemorrhage can be predicted more accurately as the number of inputs increases.
Figure 4
AUROC and AUPRC curves in the MIMIC-IV test and validation sets. (A) ROC curves for the different models depending on the number of input variables. (B) Precision-recall curves for the different models depending on the number of input variables. Model 3, which achieved the highest performance, was evaluated with an external dataset. (C) ROC curves for the eICU validation set. (D) Precision-recall curves for the eICU validation set. AUROC: area under the receiver operating characteristic curve, AUPRC: area under the precision-recall curve, MIMIC: Medical Information Mart for Intensive Care, ROC: receiver operating characteristic.

A subgroup of cases from the eICU database was selected by limiting the cases to those in which sufficient input variables were present, and 220 ICU admissions (44 cases of bleeding, 176 cases with no bleeding) were used for external validation. The general characteristics of the patients in the eICU database are listed in
Table 5.
Table 5
Baseline characteristics in the eICU dataset
|
eICU |
|
|
Hemorrhage case |
Control |
p-value |
|
Number of ICU admissions |
44 |
176 |
|
|
|
Age (yr) |
59.0 ± 14.0 |
61.2 ± 17.0 |
0.43 |
|
|
Sex |
|
Male |
24 (54.5) |
90 (51.1) |
0.16 |
|
Female |
20 (45.5) |
86 (48.9) |
|
|
|
Care unit |
|
MICU |
5 (11.4) |
17 (9.7) |
0.80 |
|
SICU |
8 (18.2) |
11 (6.2) |
|
|
Med-Surg ICU |
17 (38.6) |
96 (54.5) |
|
|
CCU-CTICU |
8 (18.2) |
39 (22.2) |
|
|
CSICU |
5 (11.4) |
8 (4.5) |
|
|
NICU |
1 (2.3) |
5 (2.8) |
|
|
|
Length of stay (day) |
8.6 ± 6.3 |
8.7 ± 6.4 |
0.94 |

We externally evaluated model 3, which showed the highest performance, using a subgroup of the eICU database. In the external validation analysis, model 3 obtained an accuracy of 0.79, a sensitivity of 0.38, a specificity of 0.88, and an AUROC of 0.74 (
Table 6). This performance was somewhat lower than was observed for the test set.
Figure 4 shows the AUROC and AUPRC curves for the eICU dataset.
Table 6
Predictive model performance in the eICU validation set
|
Accuracy |
PPV |
NPV |
Sensitivity |
Specificity |
F1-score |
AUROC |
AUPRC |
|
eICU |
0.79 |
0.44 |
0.86 |
0.38 |
0.88 |
0.41 |
0.74 |
0.39 |

IV. Discussion
In this study, we developed a machine learning model that uses structured electronic healthcare data to predict the risk of hemorrhage among patients admitted to the ICU. The model was designed to predict hemorrhage 3 hours before occurrence using sequential input of 12 hours of clinical observation data. We evaluated three models with an increasing number of input features. Model 3, which used the most input variables, showed the best performance, with a sensitivity of 0.81, specificity of 0.90, and AUROC of 0.94. Of note, the MIMIC-III and MIMIC-IV databases used different data collection periods, enabling the verification of retrospectively collected data using prospective data.
Model 1 used basic patient status and the most frequently measured vital sign parameters. In model 2, the CBC indicators had close correlations with bleeding and patient consciousness. In model 3, all the extracted and available variables were used as inputs. The best performance was observed for model 3, suggesting that performance could be improved by constructing models that learn the complexity of increasing amounts of data and by having models learn sequentially changing patient data while increasing the input variables. Additionally, we can estimate variables’ contributions to the prediction of bleeding by comparing the performance of the model depending on the added features.
Our model shows the potential to derive predictive output by monitoring individual patients in clinical settings. However, when a model is generally intended to be applied in actual clinical practice, there may be conflicts between increasing complexity and achieving stable generalization. Model 1 had the highest measurement frequencies, but did not show good predictive performance. It seems that the amount of information in model 1 alone was insufficient to predict bleeding. Model 2 showed better performance than model 1 because a sufficient data measurement frequency was ensured and a variable related to bleeding was added. All available additional variables were used in model 3, which showed the highest performance. In practice, it is rare for all patient data, including laboratory results, to be available on time, without missing values. Depending on the situation, model 2 or model 3 (or, potentially, an even more detailed model) could be used. There remains a need for attempts to determine the optimal balance, in a flexible and situation-specific manner, between the advancement of the model and its practical applicability in clinical practice.
Several tools have been developed to predict the risk of bleeding, but most are limited to patients with cardiovascular disease or those taking antithrombotic drugs [
27–
29]. An RNN-based model for predicting bleeding complications within 24 hours among patients after cardiac surgery showed an AUROC of 0.87 [
20]. An ensemble machine learning model that predicted blood transfusion among patients with gastrointestinal bleeding in the ICU using the MIMIC-III and eICU databases showed an AUROC of 0.8035 [
22]. In a study aiming to predict hemorrhage within 24 hours among surgical intensive care unit patients using several machine learning methods, a machine learning model based on least absolute shrinkage and selection operator (LASSO) regression showed an AUROC of 0.921, one based on random forests showed an AUROC value of 0.922, one based on a support vector machine (SVM) showed an AUROC value of 0.827, and an artificial neural network (ANN)-based machine learning model showed an AUROC of 0.894 [
30]. Overall, studies on the development of machine learning models for predicting bleeding as an overall emergency clinical event, without limiting such models based on the patient’s history, are rare. In this study, we constructed a model for predicting all emergency bleeding events requiring blood transfusion for all patients admitted to the ICU, and our proposed model achieved performance levels comparable to those of other machine learning models proposed in previous studies.
Our proposed model demonstrated the possibility of the early detection of severe bleeding in clinical settings, and it can be used to ensure timely follow-up measures, such as massive transfusion, surgery, or vascular embolization. Specifically, when bleeding occurs among patients with severe conditions that require intensive care, if early intervention is not performed immediately, delays could threaten patient safety, thereby resulting in a significant deterioration of their health. Additionally, because blood banks are used to store and transport blood products among various hospitals, there exists an inevitable turnaround time between entering orders and the actual transfusions. Further, the supply of blood products may not always be stable. Therefore, detecting severe blood loss in advance could substantially improve the efficiency of blood supply management strategies.
This study has several limitations. First, this study used open relational databases specialized for ICUs, thereby making it difficult to obtain data pertinent to patients’ history before entering the ICU. Therefore, patients who experienced bleeding during the early stage of admission did not have sufficient data to use as input for the model. As a result, such patients were excluded from the model training process, reducing the sample size. Another limitation is that the resolution of the data over time was different for each input variable, and we collected information only from structured data. However, many recent studies have collected and actively used various types of unstructured medical data, such as high-resolution images, videos, and biosignals. In future studies, we must expand the model structure applied in this study to follow-up datasets from the time patients are admitted to hospitals and obtain various types of data containing additional information regarding patients to improve the performance of our proposed prediction model.
External verification was performed using data obtained from the eICU database to confirm the robustness and generalizability of the model. However, the results were somewhat poorer than the initial performance of this model. Because the eICU database comprises data obtained from various ICUs across the United States, the clinical data were more heterogeneous than those obtained from the MIMIC databases. There were missing blood test results, and the frequency of data measurements was low. Therefore, we performed external validation in limited subgroups, whereby the patients had measurements of all the input features more than once during the observation window. Despite these limitations, given an AUROC of 0.74, we suggest that our proposed model is worth further external verification in multiple institutions. Additionally, to enhance the effectiveness of prediction in clinical environments, it is imperative to present changing predictive results in various windows depending on the patient. In clinical practice, critical patients’ status is monitored in real time, and predictive models require continuous input data updates from admission and prediction results according to changes in patients’ status to ensure efficiency in real-world environments. In our future studies, we plan to construct our proposed model using a sliding window to support clinical decision-making.
In conclusion, our proposed machine learning model has potential for utilization as a tool for monitoring patients, with the main aim of identifying ICU patients at a high risk of bleeding in advance.








 PDF
PDF Citation
Citation Print
Print



 XML Download
XML Download