Abstract
Background
The direct method for reference interval (RI) estimating is limited due to the requirement of resources, difficulties in defining a non-diseased population, or ethical problems in obtaining samples. We estimated the RI for inflammatory biomarkers using an indirect method (RII).
Methods
C-reactive protein (CRP), erythrocyte sedimentation rate (ESR) and presepsin (PSEP) data of patients visiting a single hospital were retrieved from April 2009 to April 2021. Right-skewed data were transformed using the Box-Cox transformation method. A mixed population of non-diseased and diseased distributions was assumed, followed by latent profile analysis for the two classes. The intersection point of the distribution curve was estimated as the RI. The influence of measurement size was evaluated as the ratio of abnormal values and adjustment (n×bandwidth) of the distribution curve.
Results
The RIs estimated by the proposed RII method (existing method) were as follows CRP, 0–4.1 (0–4.7) mg/L; ESR, 0–10.2 (0–15) mm/hr and PSEP, 0–411 (0–300) pg/mL. Measurement sizes ≥2,500 showed stable results. An abnormal-to-normal value ratio of 0.5 showed the most accurate result for CRP. Adjustment values ≤5 or >5 were applicable for a measurement size <25,000 or ≥25,000, respectively.
Interpretation of laboratory datasets requires comparison to a reference interval (RI), which focuses on optimizing specificity. The RI should be determined by maximum intervals that could cover a non-diseased population and exclude a diseased population. Determination of the RI is a prerequisite for clinical decision-making or evidence-based medicine. Grasbeck and Saris [1] proposed the concept of an RI, which has been widely adopted for medical decision-making [2]. A direct method for estimating the RI (RID) involves a unimodal approach, in which the RI is defined by measuring the analytes of a non-diseased group and taking the central 95% or 95th percentile of the selected non-diseased population [1-3]. The bimodal approach for estimating the RID includes measurements from both non-diseased and diseased populations, followed by receiver operating characteristic curve analysis, applying the maximal efficiency concept, maximal-likelihood concept, the intersection of the distribution curve, or the inflection point of the discriminant curve [2]. However, this prospective RID estimation method requires extensive resources and time, and defining a non-diseased (reference) population requires rigorous and strict criteria based on questionnaires [1, 4]. Samples from neonates and children can provoke ethical problems or are often insufficient in number, whereas those from elderly groups are often complicated as a reference owing to the higher rates of comorbidities or medical problems in this population.
RI estimation by an indirect method (RII) is an area of active research, which involves statistical analyses of accumulated laboratory data [4, 5]. Although a method for RII estimation is yet to be validated, the availability of large datasets along with increasing computation power and research tools have increased the feasibility of indirect RI determination [6-10]. A unimodal approach could be used as an RII method by collecting data from non-diseased populations and discarding data or extreme values from the non-diseased populations. Alternatively, a bimodal approach assumes the presence of a non-diseased group and diseased group within a dataset. This approach enables using data with mixed populations without necessarily discarding extreme values and determining a cut-off value at the upper end of one side. The reference limit could then be defined by the same method used in RID along with the intersection of the distribution curve [1, 11, 12].
This study was approved by the Institutional Review Board of Seoul St. Mary’s Hospital, The Catholic University of Korea, Seoul, Korea (KC21WASI0638). De-identified inflammatory marker (C-reactive protein [CRP], erythrocyte sedimentation rate [ESR], presepsin [PSEP]) data were retrieved from the hospital laboratory information system of the Clinical Data Warehouse of the Catholic Information Convergence Institute, The Catholic University of Korea. CRP (1,392,356 measurements, N=353,340 patients), ESR (951,497 measurements, N=206,894 patients), and PSEP (4,219 measurements, N=1,086 patients) data were retrieved from April 2009 to April 2021. CRP was measured using a Hitachi 7,600 system (Hitachi, Tokyo, Japan), ESR was measured using the TEST-1 system (Alifax, Padova, Italy), and PSEP was measured by PATHFAST (LSI Medience Corporation, Tokyo, Japan).
A histogram of the data was plotted and analyzed. To determine the distribution curve of the histogram, kernel density estimation was performed, which is a nonparametric approach to estimate the probability density function of a variable. These estimates are determined from a histogram of a total measurand using the R package kdensity [1, 17-19]. Box-Cox transformation was performed to normalize the distribution of skewed data. The maximum-likelihood method was applied to obtain the lambda parameter for Box-Cox transformation, which was calculated by the R package MASS [18, 19].
Latent profile analysis (LPA) is an analytical method that provides a categorical latent variable from continuous data. LPA tries to identify latent or unknown subpopulations within a population and assigns a measurand to a latent group with a certain degree of probability. We used LPA with the R package tidyLPA [20-27] to assign certain values to the non-diseased group and other values to diseased groups. For LPA, variances are regarded as equal variables between two profiles, whereas covariance is regarded as zero because there is only one measured biomarker applied for analysis at a time. Since we hypothesized that there are two profiles, a bimodal approach was used and two-model analyses were selected for LPA. Multiple profiles among biomarkers are possible to obtain an analytical result based on Akaike’s information criterion, the Bayesian information criterion, entropy, or other parameters. As the focus of this study was to distinguish non-diseased and diseased groups, we assumed only two profiles among the tested variables. Mean values with two standard deviations are denoted followed by two distribution curves over Box-Cox–transformed data based on the LPA results. The distribution curves of the non-diseased and diseased groups are then plotted.
The intersection of the distribution curve was regarded as the reference limit for the non-diseased and diseased populations. These intersection values maximize the accuracy of RIs. Determination of the intersection point was associated with the bandwidth or adjustment (n×bandwidth) of the distribution curve. Smaller adjustment resulted in an overfitting distribution curve, whereas larger adjustment resulted in a smoothed distribution curve. The value of the intersection point was directly influenced by the adjustment value. The intersection point was determined at the point with the smallest adjustment showing a non-overfitting graph, which was selected based on the feature of a smoothed distribution plot showing one mode [20]. Factors that influenced the estimated RI were searched, and the measurement size and ratio of abnormal CRP values among total measurements and adjustment value were analyzed based on CRP data. Abnormal CRP values (>4.7) or normal CRP values (0–4.7 mg/L) were based on the established institutional RI. Abnormal CRP values were extracted from a 10% to 90% ratio among 10,000 measurements to analyze the effect of an abnormal value ratio on the cut-off line.
For PSEP, the data were stratified according to age based on 5-year intervals and age group of ≥50 years or <50 years, as well as sex. Monthly means were plotted to visualize the drift effect, and the F-test and cumulative sums of standardized residuals (cusum) test were performed using the R package strucchange [17]. PSEP values are known to be affected by renal clearance or hemoglobin levels, which could affect the RI estimates; therefore, additional analysis was performed for PSEP [28, 29] in which the data were also stratified by hospital ward.
Measurements were grouped by age categories in a 10-year age groups. Mean, SD, median, and interquartile range were noted for each age group by sex difference. Kernel density estimate was performed to investigate statistical skewness, bimodality or polymodality, and other factors. The lambda parameter for Box-Cox transformation was calculated using the maximum-likelihood method. R software version 3.4.4 (Free Software Foundation, Inc., Boston, MA, USA) was used for all analyses.
Normal or abnormal CRP values along with extreme values were included, as these values would be part of real-world data (Table 1).
The histogram of CRP showed a right-skewed pattern (Fig. 1A). Kernel density estimation (Fig. 1B) and Box-Cox transformation were performed (Fig. 1C, D). We hypothesized that there are two profiles of the non-diseased or diseased populations within these datasets for LPA (Fig. 1E). The histogram was converted to a distribution curve, and the intersection value from the non-diseased and diseased density curves was calculated to find the intersection value (Fig. 1F) of −0.91195, which was converted to 4.11 mg/L. Conversion of the Box-Cox–transformed value (BC) was performed using the exponential of BC if lambda (λ) was zero or exponential of log(λ×BC+1)×(1/λ), if λ was not zero. Therefore, the RI cut-off value was determined as 4.1 mg/L, which was equivalent to the institutional RI (0–4.7 mg/L) (Table 2).
The influence of measurement size, ratio of abnormal values, and adjustment (n×bandwidth) on RI estimates was analyzed using the CRP dataset (Fig. 2). The measurement size was evaluated using two adjustment values of 5 or 10. Because the distribution curve showed an overfitting pattern among higher measurements, an adjustment of ≥6 or ≤5 was evaluated, respectively. A measurement size ≥25,000 showed stable results for an adjustment of 10 (Fig. 2A), whereas an adjustment value of 5 showed stable results for a measurement size of ≤25,000. A measurement size <1,000 showed a large SD, which was inappropriate for analysis. Measurement sizes ≥2,500 are suggested and an adjustment value ≤5 is suggested for a measurement size ≤25,000, whereas adjustment values >5 are suggested for measurement sizes >25,000.
Abnormal-to-normal values of CRP were defined according to the institutional RI (CRP ≤4.7 mg/L). Abnormal or normal values were extracted without replacement, and the abnormal value ratio was extracted from the 10% to 90% among 10,000 measurements. Abnormal CRP values from 45% to 55% showed an estimated RI near the expected value of 4.7 mg/L (Fig. 2B).
The adjustment value was also evaluated for determination of the CRP cut-off. As CRP had >25,000 measurements, adjustment values of ≤5 were used (Fig. 2A, C). Estimation of the adjustment value was selected by a visual graphical method.
The RII method based on CRP measurements was then applied to ESR and other inflammatory markers. For ESR RI analysis, the same analytical method was applied (Table 1, Supplemental Data Table S1). The histogram of ESR showed a right-skewed pattern (Supplemental Data Fig. S1A). Kernel density estimation (Supplemental Data Fig. S1B) followed by Box-Cox transformation was performed (Supplemental Data Fig. S1C) using the λ parameter 0.02020202. LPA showed a mean (2SD) of 1.24 (−0.375 to 2.855) and 3.20 (1.584 to 4.815) for the non-diseased and diseased population, respectively (Supplemental Data Fig. S1D, E). The intersection of distribution curves resulted in a value of 2.3872 (10.2 mm/hr), which was slightly lower or equivalent to that of the institutional RI of 0–14 mm/hr (males) or 0–20 mm/hr (females) (Supplemental Data Fig. S1F).
There were 3,485 and 708 PSEP measurements from patients aged ≥50 years and <50 years, respectively, and both histograms showed right-skewed patterns (Supplemental Data Fig. S2A). Mean (SD) values for patients aged ≥50 years and <50 years were 1,514 pg/mL (2,944) and 1,355 pg/mL (3,370), respectively (Supplemental Data Table S2). There were 2,560 and 1,633 measurements from males and females, respectively, showing similar right-skewed patterns (Supplemental Data Fig. S2B), and the mean (SD) values were 1,715 pg/mL (3,543) and 1,130 pg/mL (1,879), respectively (Supplemental Data Table S2).
PSEP values were plotted by month over a 1-year period, exhibiting drift or structural change by the F-test (P=0.0000105) but not by the cusum test (P=0.05767) (Supplemental Data Fig. S2C). The test stratified for each ward showed higher mean values in medical intensive care units compared with that in other wards, but with a large mean SD (Supplemental Data Fig. S2D). The histogram of PSEP measurement showed a right-skewed pattern (Supplemental Data Fig. S3A). Kernel density estimation was performed (Supplemental Data Fig. S3B), followed by Box-Cox transformation (Supplemental Data Fig. S3C and S3D) using the λ parameter −0.3030303. Normality was rejected by the Kolmogorov-Smirnov test (P<0.0001) for Box-Cox–transformed data. Instead of the percentile method, LPA was applied for determination of the RI.
LPA showed a mean (2SD) of 2.73 (2.51–2.94) and 2.91 (2.68–3.13) for the non-diseased and diseased population, respectively (Supplemental Data Fig. S3E). The mean (2SD) of class one and two is plotted as the green and red line (dotted line), respectively, representing the non-diseased and diseased group, respectively. The intersection value of the distribution curve resulted in a value of 2.891, which could be converted to 411 pg/mL (Supplemental Data Fig. S3F). Based on these analyses, the RI cut-off value for PSEP using the indirect method was determined to be 411 pg/mL.
The RI estimated by the indirect method (institutional RIs in parentheses) were as follows: CRP, 0–4.1 (0–4.7) mg/L; ESR, 0– 10.2 (0–15) mm/hr; PSEP, 0–411 (0–300) pg/mL.
The RI is a fundamental concept for the interpretation of laboratory data. Determination of the RI could provide a value for diagnosis, prognosis, or clinical decision-making. In the case of sepsis, inflammatory markers such as CRP, ESR, cytokines, chemokines, PSEP, or procalcitonin are used for diagnosis or prognosis [13-16, 29, 30].
The RID has been regarded as the standard method for RI estimation. Reference data could be obtained from a minimum of 120 healthy individuals. Age, sex, comorbidities, social habits, and other characteristics could be used to stratify a population or as enrollment criteria for analysis. High costs and ethical problems hinder the establishment of RIs for laboratories [1, 2, 31]. Defining a non-diseased condition requires consensus for studied biomarkers. Biological variation among individuals or analytical methodology of measurements should be considered when interpreting the RID.
RII methods have also been studied and applied to various biomarkers. However, the criteria for the number of measurements, partitioning, or inclusion and exclusion should be defined or studied. Optimal statistical methods are required for determination of the RIs of biomarkers. The Bhattacharya or Hoffmann method assumes a Gaussian distribution of measurements. An alternative method is thus needed for biomarkers with a skewed distribution, as found in this study [4-12, 32].
In this study, the data were regarded to come from a mixed population of non-diseased and diseased groups; accordingly, all values were included for analysis, including extreme values. Defining a healthy or non-diseased state was unnecessary in this statistical process. Decomposition of the mixture distribution was performed using LPA, which applies an expectation maximization algorithm [25, 33]. LPA assumes unobserved population heterogeneity, which suits the purpose of finding mixed populations using continuous variables. The accuracy of LPA could be improved by including patient data along with extreme values that might result in the clear identification of classes. LPA could be applied for the determination of hidden classes within a large number of datasets. Although LPA is robust to outliers and data from diseased populations [21-25], this method is sensitive to starting values that might lead to local rather than global optimization. There could be more than two populations among the whole distribution, which was not considered in our analysis.
Multiple measurements from individual patients were included for analysis since measurements of inflammatory markers are assumed to represent a patient state that would fluctuate over time. As the patient state could change, each data point is still assumed to be independent. Although some measurements were derived from the same patient, the measurements from a diseased state or non-diseased state would still be different. Further studies are required to determine whether these multiple repeated measurements influence the distribution of the population that could in turn influence RI estimates.
The determination of RIs for inflammatory markers, especially for cytokines, is hindered by high costs and various test methods. The proposed RII approach might support the current RI or institutional RI with low evidence levels compared to other frequently tested biomarkers. Inflammatory markers showed a wide measurement range from 1 to 20,000 pg/mL for PSEP. We estimated RI by the indirect method for three inflammatory markers including all the data. The number of abnormal values influences the reference limit and the inclusion of more abnormal values tended to increase the RI [23]. For ESR, the normal-to-abnormal result ratio might have lowered the RI estimate. These distributions with higher normal measurements might reflect the actual population distribution.
We minimized selection bias by including all the measured values obtained during the defined period. Since the adjustment value or bandwidth was determined according to the research purpose or by the subjective decision of the researcher, further studies are required to optimize the adjustment value or bandwidth for a large dataset. Further studies are also required to establish sophisticated mathematical equations that could determine bandwidth or adjustment values for large populations along with feasible computation methods.
The frequency of RII verification is unknown. We considered that changes in patient characteristics such as age, sex, diagnosis, or ratio of non-diseased or diseased individuals might have influenced the distribution. These factors could be considered for determining the verification frequency in further studies. This study showed that simulation of a measurement size below 10,000 had higher variance; we suggest performing frequent RI verification with additional accumulated data.
The RI for PSEP estimated with our RII method was 0–411 pg/mL, which is higher than previous results with a mean value ranging from 21.8 to 382 pg/mL [33] or that of the institutional RI. This difference might have been caused by the inclusion of higher values rather than lower values from non-diseased populations, which would have shifted the cut-off value toward the higher side. As the PSEP level is influenced by renal function and hemoglobin, a population with these comorbidities might have shifted cut-off values to the higher side [29].
Based on these data, RI estimation could be performed using an indirect method. This method requires the following assumptions: (1) the analysis procedure could be performed for right-skewed data; (2) the measurement size should be more than 2,500; and (3) two classes of the latent variable are of similar size, which is unknown. Box-Cox transformation followed by LPA for two classes was performed. If the measurement size was larger than 25,000, an adjustment value greater than 5 could be applied. Visual graphical evaluation is possible to obtain an adequate adjustment value. Intersection values of the non-diseased and diseased population distributions could be obtained. If the measurement size is smaller than 10,000, RI should be verified until sufficient data are collected for analysis. If the measurement size is large, RI verification could be performed when necessary (Supplemental Data Fig. S4). Revision or verification of the RI is required when the reagents or analyzer are replaced or changed. Changes in the characteristics of patients, such as diagnosis, age, and sex, may also require revision.
The main limitation of this study is that LPA was performed on the assumption that there are non-diseased and diseased classes within a mixed population. However, there could be multiple classes within non-diseased or diseased classes. The distribution intersection values were determined by a visual graphical method along with adjustment (n×bandwidth). The proportion of normal or abnormal results and the sample sizes affected RI estimates. RI values were influenced by the given distribution, and we did not obtain 95% confidence intervals in our statistical procedure. The statistical process was applied to right-skewed data, and thus, additional studies are required for two-sided data.
In conclusion, RI estimated by an indirect method could provide additional information for verification or determination of the RI in clinical laboratories. RII estimates of CRP, ESR, and PSEP showed comparable results with the institutional RIs.
ACKNOWLEDGMENTS
We thank Sujung Kim and Grace Cha (Sysmex Korea Inc.) for the technical assistance, and Ae Ran Choi, Eui Sik Lee, Jeong-Jong Lee, and Kyong-Ho Cha (Laboratory Medicine, Seoul St. Mary’s Hospital) for technical advice. We also thank Min Kyung Jung and Yeonheee Seo (Catholic Information Convergence Institute, The Catholic University of Korea) for data retrieval and coordination.
Notes
AUTHOR CONTRIBUTIONS
Kang T and Yoo J analyzed the data and drafted the manuscript. Jekarl DW designed the study, analyzed the data, and drafted the manuscript. Kim Y designed and supervised the study and drafted the manuscript. Chae H and Oh E-J performed data curation and validated the study. Kim M and Park Y-J secured resources for this study. All authors accept responsibility for the entire content of this manuscript and approve its submission.
REFERENCES
1. Grasbeck R, Saris NE. 1969; Establishment and use of normal values. Scand J Clin Lab Investig Suppl. 110:62–3.
2. Haeckel R, Wosniok W, Arzideh F. 2007; A plea for intra-laboratory reference limits. Part 1. General considerations and concept for determination. Clin Chem Lab Med. 45:1033–42. DOI: 10.1515/CCLM.2007.249. PMID: 17867993.
3. CLSI. 2008. Defining, establishing, and verifying reference intervals in the clinical laboratory. Approved guideline. 3rd ed. CLSI document c28-A3. Clinical and Laboratory Standards Institute;Wayne, PA:
4. Ozarda Y, Higgins V, Adeli K. 2018; Verification of reference intervals in routine clinical laboratories: practical challenges and recommendations. Clin Chem Lab Med. 57:30–7. DOI: 10.1515/cclm-2018-0059. PMID: 29729142.

5. Zierk J, Arzideh F, Kapsner LA, Prokosch HU, Metzler M, Rauh M. 2020; Reference interval estimation from mixed distributions using truncation points and the Kolmogorov-Smirnov distance (kosmic). Sci Rep. 10:1704. DOI: 10.1038/s41598-020-58749-2. PMID: 32015476. PMCID: PMC6997422.

6. Ozarda Y, Sikaris K, Streichert T, Macri J. IFCC Committee on Reference Intervals and Decision Limits (C-RIDL). 2018; Distinguishing reference intervals and clinical decision limits-a review by the IFCC Committee on Reference Intervals and Decision Limits. Crit Rev Clin Lab Sci. 55:420–31. DOI: 10.1080/10408363.2018.1482256. PMID: 30047297.
7. Martinez-Sanchez L, Marques-Garcia F, Ozarda Y, Blanco A, Brouwer N, Canalias F, et al. 2021; Big data and reference intervals: rationale, current practices, harmonization and standardization prerequisites and future perspectives of indirect determination of reference intervals using routine data. Adv Lab Med. 2:9–16. DOI: 10.1515/almed-2020-0034.

8. Holmes DT, Buhr KA. 2019; Widespread incorrect implementation of the Hoffmann method, the correct approach, and modern alternatives. Am J Clin Pathol. 151:328–36. DOI: 10.1093/ajcp/aqy149. PMID: 30475946.

9. Manrai AK, Patel CJ, Ioannidis JPA. 2018; In the era of precision medicine and big data, who is normal? JAMA. 319:1981–2. DOI: 10.1001/jama.2018.2009. PMID: 29710130. PMCID: PMC7572221.

10. Obstfeld AE, Patel K, Boyd JC, Drees J, Holmes DT, Ioannidis JPA, et al. 2021; Data mining approaches to reference interval studies. Clin Chem. 67:1175–81. DOI: 10.1093/clinchem/hvab137. PMID: 34402506.

11. Lahti A, Hyltoft Petersen P, Boyd JC. 2002; Impact of subgroup prevalences on partitioning of Gaussian-distributed reference values. Clin Chem. 48:1987–99. DOI: 10.1093/clinchem/48.11.1987. PMID: 12406985.

12. Arzideh F, Wosniok W, Gurr E, Hinsch W, Schumann G, Weinstock N, et al. 2007; A plea for intra-laboratory reference limits. Part 2. A bimodal retrospective concept for determining reference limits from intra-laboratory databases demonstrated by catalytic activity concentrations of enzymes. Clin Chem Lab Med. 45:1043–57. DOI: 10.1515/CCLM.2007.250. PMID: 17867994.

13. Jekarl DW, Kim JY, Lee S, Kim M, Kim Y, Han K, et al. 2015; Diagnosis and evaluation of severity of sepsis via the use of biomarkers and profiles of 13 cytokines: a multiplex analysis. Clin Chem Lab Med. 53:575–81. DOI: 10.1515/cclm-2014-0607. PMID: 25274957.

14. Jekarl DW, Kim JY, Ha JH, Lee S, Yoo J, Kim M, et al. 2019; Diagnosis and prognosis of sepsis based on use of cytokines, chemokines, and growth factors. Dis Markers. 2019:1089107. DOI: 10.1155/2019/1089107. PMID: 31583025. PMCID: PMC6754872.

15. Jekarl DW, Lee S, Kim M, Kim Y, Woo SH, Lee WJ. 2019; Procalcitonin as a prognostic marker for sepsis based on SEPSIS-3. J Clin Lab Anal. 33:e22996. DOI: 10.1002/jcla.22996. PMID: 31420921. PMCID: PMC6868407.

16. Kim KS, Jekarl DW, Yoo J, Lee S, Kim M, Kim Y. 2021; Immune gene expression networks in sepsis: a network biology approach. PLoS Oone. 16:e0247669. DOI: 10.1371/journal.pone.0247669. PMID: 33667236. PMCID: PMC7935325.

17. Farrell CL, Nguyen L. 2019; Indirect reference intervals: harnessing the power of stored laboratory data. Clin Biochem Rev. 40:99–111. DOI: 10.33176/AACB-19-00022. PMID: 31205377. PMCID: PMC6544248.

18. Zeileis A, Leisch F, Hornik K, Kleiber C. 2002; strucchange: an R package for testing for structural change in linear regression models. J Stat Softw. 7:1–38. DOI: 10.18637/jss.v007.i02.
19. Moss J, Tveten M. 2019; kdensity: an R package for kernel density estimation with parametric starts and asymmetric kernels. J Open Source Softw. 4:1566–9. DOI: 10.21105/joss.01566.

20. Ripley B, Venables B, Bates D, Hornik K, Gebhardt A, Firth D. 2002. Modern applied statistics with S. 4th ed. Springer;Switzerland: DOI: 10.1007/978-0-387-21706-2.
21. Bauer DJ, Curran PJ. 2004; The integration of continuous and discrete latent variable models: potential problems and promising opportunities. Psychol Methods. 9:3–29. DOI: 10.1037/1082-989X.9.1.3. PMID: 15053717.

22. Ekblom-Bak E, Stenling A, Eriksson SJ, Hemmingsson E, Kallings LV, Andersson G, et al. 2020; Latent profile analysis pattern of exercise, sitting and fitness in adults-association with metabolic risk factors, perceived health, and perceived symptoms. PLoS One. 15:e0232210. DOI: 10.1371/journal.pone.0232210. PMID: 32330191. PMCID: PMC7182226.
23. Rosenberg JM, Beymer PN, Anderson DJ, van Lissa CJ, Schmidt JA. 2018; tidyLPA: an R package to easily carry out latent profile analysis (LPA) using open-source or commercial software. J Open Source Softw. 3:978–81. DOI: 10.21105/joss.00978.

24. Morgan GB, Hodge KJ, Baggett AR. 2016; Latent profile analysis with nonnormal mixtures: a Monte Carlo examination of model selection using fit indices. Comput Stat Data Anal. 93:146–61. DOI: 10.1016/j.csda.2015.02.019.

25. Tein JY, Coxe S, Cham H. 2013; Statistical power to detect the correct number of classes in latent profile analysis. Struct Equ Modeling. 20:640–57. DOI: 10.1080/10705511.2013.824781. PMID: 24489457. PMCID: PMC3904803.

26. Robertson J, Kaptein M. 2016. Modern statistical methods for HCL. Springer;Switzerland: DOI: 10.1007/978-3-319-26633-6.
27. Spurk D, Hirschi A, Wang M, Valero D, Kauffeld S. 2020; Latent profile analysis: a review and "how to" guide of its application within vocational behavior research. J Vocat Behav. 120:103455. DOI: 10.1016/j.jvb.2020.103445.

28. Hyohdoh Y, Hatakeyama Y, Okuhara Y. 2021; A simple method to identify real-world clinical decision intervals of laboratory tests from clinical data. Inform Med Unlocked. 23:100512. DOI: 10.1016/j.imu.2021.100512.

29. Kang T, Yoo J, Choi H, Lee S, Jekarl DW, Kim Y. Performance evaluation of presepsin using a Sysmex HISCL-5000 analyzer and determination of reference interval. J Clin Lab Anal. 2022; e24618. DOI: 10.1002/jcla.24618. PMID: 35870180.
30. Jekarl DW, Lee SY, Lee J, Park YJ, Kim Y, Park JH, et al. 2013; Procalcitonin as a diagnostic marker and IL-6 as a prognostic marker for sepsis. Diagn Microbiol Infect Dis. 75:342–7. DOI: 10.1016/j.diagmicrobio.2012.12.011. PMID: 23391607.

31. Sung JY, Seo JD, Ko DH, Park M, Hwang SM, Oh S, et al. 2021; Establishment of pediatric reference intervals for routine laboratory tests in Korean population: a retrospective multicenter analysis. Ann Lab Med. 41:155–70. DOI: 10.3343/alm.2021.41.2.155. PMID: 33063677. PMCID: PMC7591287.

32. Jones GRD, Haeckel R, Loh TP, Sikaris K, Streichert T, Katayev A, et al. 2018; Indirect methods for reference interval determination- review and recommendations. Clin Chem Lab Med. 57:20–9. DOI: 10.1515/cclm-2018-0073. PMID: 29672266.
33. Kim CH, Kim EY. 2021; Prediction of postoperative sepsis based on changes in presepsin levels of critically ill patients with acute kidney injury after abdominal surgery. Diagnostics. 11:2321. DOI: 10.3390/diagnostics11122321. PMID: 34943556. PMCID: PMC8700401.

Fig. 1
Estimation of CRP reference interval by the indirect method (N=353,340 measurements; N=1,392,356 individuals). The non-diseased population is denoted as mean (2SD) as a green line (dotted line), and the diseased population is denoted as mean (2SD) as a red line (dotted line). The mean (2SD) resulted from latent profile analysis. (A) Histogram of data. (B) Kernel density plot. (C) Box-Cox transformation. (D) Distribution of Box-Cox–transformed data. (E) Latent profile analysis defined two classes with the mean value (straight line) and 2SD (dotted line). (F) Density plot for the two classes with the intersecting point shown as the dotted line.
Abbreviation: CRP, C-reactive protein.
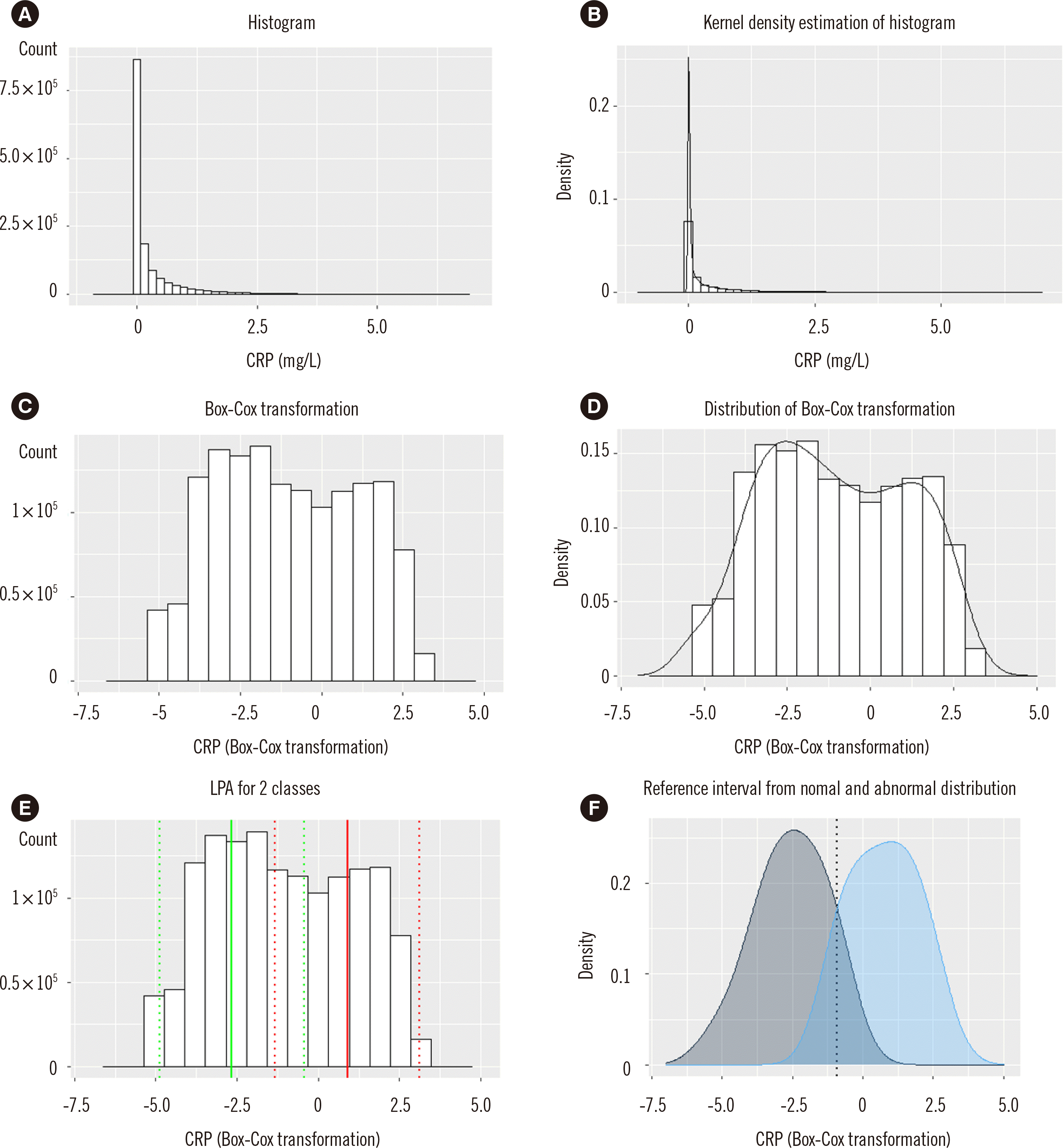
Fig. 2
Influence of various factors on reference interval (RI) estimation for CRP: (A) sample size, (B) CRP ratio among 10,000 samples, and (C) adjustment values.
Abbreviations: CRP, C-reactive protein.
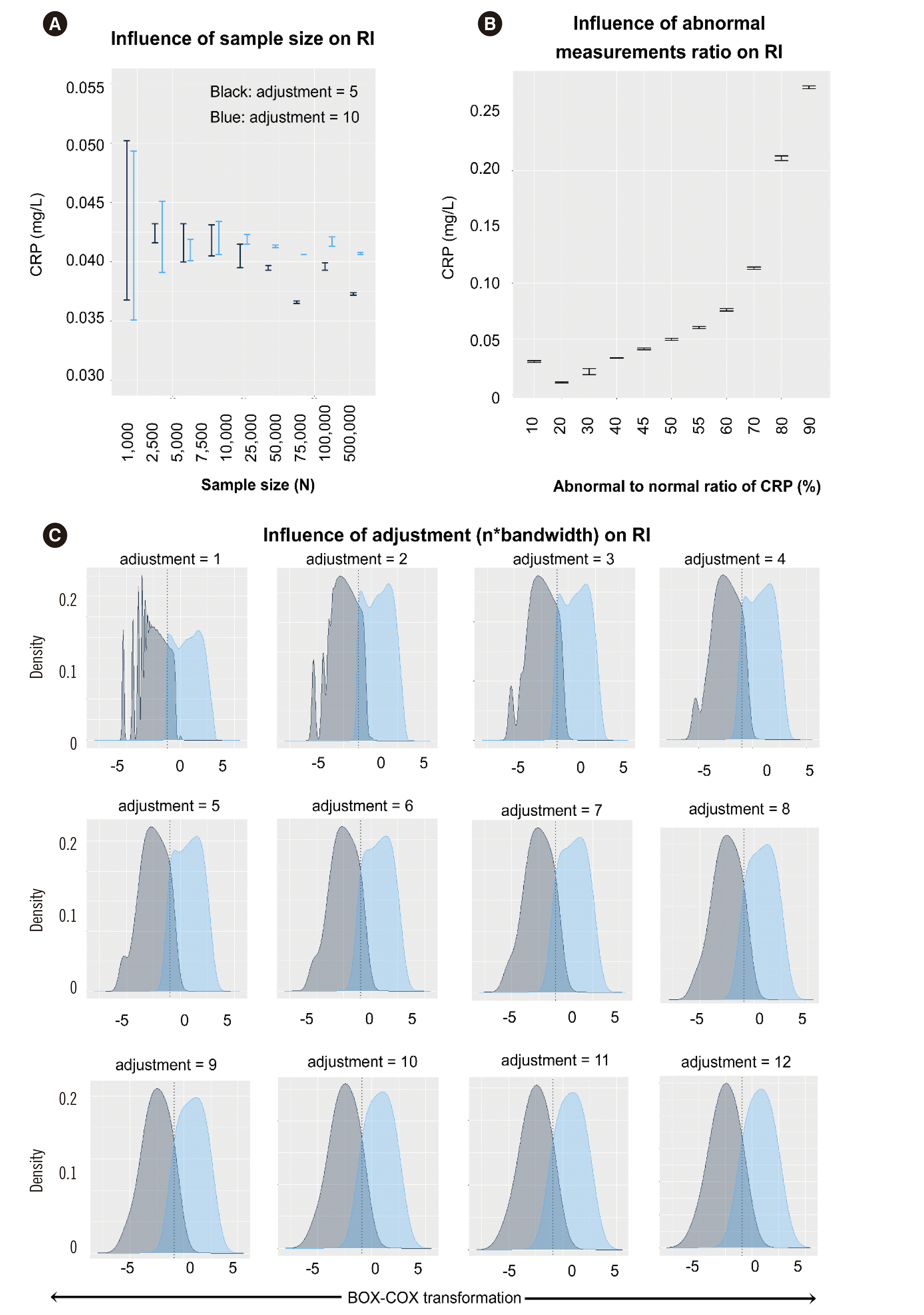
Table 1
Reference intervals for inflammatory biomarkers estimated by the indirect method
| Markers* | Measurements (N) | Individuals (N) | Box-Cox λ | LPA class 1 (μH, SD) | LPA class 2 (μD, SD) | Adjusted (n×bw) | Estimated RI | Institutional RI |
|---|---|---|---|---|---|---|---|---|
| CRP | 1,392,356 | 353,340 | −0.0606 | 0.008, 0.487 | 0.252, 0.487 | 10 | 0–4.1 | 0–4.7 |
| ESR | 951,497 | 206,894 | 0.0202 | 3.40, 0.64 | 21.81, 0.64 | 7 | 0–10.2 | 0–15 |
| PSEP | 4,219 | 1,086 | −0.3030 | 328, 1.11 | 1,149, 1.11 | 2 | 0–411 | 0–300 |
Table 2
Data of C-reactive protein (mg/L) from the database based on 1,392,356 measurements (N=353,340 individuals)




 PDF
PDF Citation
Citation Print
Print



 XML Download
XML Download