In clinical studies comparing 2 groups, researchers must show that the effect of an explanatory variable on a response variable is due only to the studied intervention. To do so, all subjects in the study should have the same characteristics. In a randomized control study, random treatment allocation ensures that the treatment status is not confounded with either measured or unmeasured baseline characteristics.1) However, in observational studies, limited control of confounding variables makes it difficult to explain causality and uncover clear medical evidence. Improving causal inference in observational studies requires statistical methods that are able to guarantee comparability between 2 comparison groups; propensity score matching (PSM) is one of these methods. For example, in their study of aspirin use and all-cause mortality among patients being evaluated for known or suspected coronary artery diseases, Gum et al.2) used PSM to match patients between the aspirin group and no aspirin group. Seung et al.3) applied PSM in their study of stents versus coronaryartery bypass grafting (CABG) for left main coronary artery disease, matching patients between the stent group and CABG group. Yao et al.4) used PSM in their study comparing surgical left atrial appendage occlusion (LAAO) with no surgical LAAO.

PSM is based on a “counterfactual” framework derived from Rubin's causal model.5) The counterfactual condition assumes that an individual in an experiment group did not participate in the experiment. Therein, the causal effect of interest to researchers would be the difference between the effect on a subject from participating in a clinical study (factual) and the effect on the subject if he/she did not participate in the study (counterfactual). For example, in a study of the effects of a new drug, the effects derived from taking the drug are factual, and those derived from not taking the drug are counterfactual. In general experimental studies, it is difficult to compare treatment effects in the same person. Since the experimental group cannot observe the situation where they do not participate in the study, a control group is established as a counterfactual to estimate the potential effect of the intervention.6)

PSM divides all subjects into 2 groups with the matching covariates as much as possible. This matching is based on propensity scores (PSs), which reflect the conditional probabilities that individuals will be included in the experimental group when covariates are controlled for all subjects. That is, the counterfactuals for the experimental group are matched between groups with close to homogeneous characteristics.

In this article, we introduce the concept of PSM, PSM methods, limitations, and statistical tools for conducting PSM.

PS is defined as the “conditional probability” that a patient i will be in the treatment group given his/her measured covariates.7) In other words, the PS is a balancing score that summarizes the covariates. If X is a dummy variable that takes on value 1 for treatment and 0 for control, and assuming that the covariate to be matched is c, the PS can be expressed as Equation 1.

Matching the same covariates, as much as possible, across two groups using the PS values from Equation 1 enables the treatment and control groups to be reconstructed with reduced selection bias. The PS corresponds to the predicted probability of the logistic regression model. In this case, the predictive probability should be obtained by using a full nonparsimonious model that includes all possible covariates investigated. Moreover, some interaction terms or squared terms should also be included. In addition, the c-statistic and suitability (Hosmer–Lemeshow statistic) of the predictive model should be examined.8 Once estimated, PS can be used to reduce bias through matching, stratification (subclassification), regression adjustment, or some combination of all 3.8)

Three assumptions are needed to apply PSM (Figure 1).9)

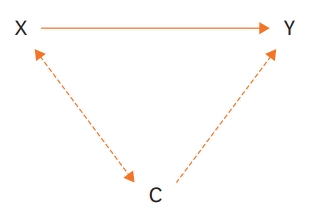
When X represents a treatment, C denotes covariates, and Y is the outcome, the following 3 assumptions can be drawn.

First, the treatment is related to the covariates:

Second, with the given covariates, the treatment is independent of the outcome:

Third, with the given covariates, the treatment is still related to the outcome because of hidden selection bias:

After PSM, a check is needed to verify that it has been performed properly. One way to check whether the PSM is appropriate is to calculate standardized mean differences. Recently, L1 statistics12) and D2 statistics13) have been proposed as alternatives. Based on these statistics, a researcher can plan PSM again.

The standardized mean difference reflects the difference in covariates between two groups using mean, variance, and proportion values, and can be assessed using the equations below. A standardized mean difference greater than 10 percent represents meaningful imbalance.14) Equations 2 and 3 reflect the case of continuous variables and categorical variables, respectively.

L112) is a multivariate imbalance measure for matching balance. Values of L1 are easily interpretable. If the distributions of two groups are completely different, then L1=1, indicating that the PSM results are imbalanced. Conversely, if the 2 distributions overlap exactly, then L1=0, indicating good balance.

D213) is a test statistic for determining the overall imbalance between treatment and control groups, that is, to evaluate whether the linear combination of covariates and covariates are unbalanced after matching. If the null hypothesis is not rejected, the structure of the 2 groups is similar, and hence, the matching is considered good. As this statistic is sensitive to the number of subjects (N), researchers should apply it with caution if N is too small.

While PSM can minimize selection bias, its limitations in practical applications should also be considered. PSM analysis requires large cohorts; an insufficient number, depending on the number of observed covariates, can make it difficult to use. It is also inappropriate to use PSs to estimate covariates that lack observations. Next, PSM relies on unverifiable assumptions (e.g., a strongly ignorable treatment assignment given the observed covariates or unobserved confounders), and therefore necessitates a sensitivity analysis. In addition, PSM requires substantial overlap between the treatment and control groups. If there are only a few overlapping regions, it can be difficult to select subjects with similar characteristics, thereby potentially leading to a significant loss of data. Moreover, in longitudinal studies, PS application requires the construction of time-dependent PSs (sequential matching) and inverse probability of treatment weighted estimator methods.15)

PSM can be implemented using statistical programs in SAS (SAS Institute, Cary, NC, USA), R (R Foundation, Vienna, Austria), SPSS (IBM Corp., Armonk, NY, USA), and STATA (StataCorp, College Station, TX, USA). After PS values are obtained using the PROC LOGISTIC function, matching is possible through the %PSmatching macro in SAS,16) MatchIt package in R,17) PSMATCH2 algorithm in STATA,18) or by integrating the R package in SPSS.19) If researchers find using SAS and R challenging, SPSS is recommended. To do so, R should be installed according to the SPSS version being used; this is possible after executing a program (SPSS® Statistics-Essentials for R) that links SPSS and R.

PSM is a useful approach for researchers to improve causal inference in observational studies. However, there are some limitations and precautions that warrant consideration.20) Accordingly, researchers ought to proceed in a manner that is appropriate for their given data.