Abstract
Purpose
Precise estimation of the standard liver volume (SLV) is crucial in decision making regarding major hepatectomy and living donor liver transplantation. This study aimed to propose an accurate and efficient formula for estimating the SLV in the Korean population.
Methods
We created a regression model for SLV estimation using a data set of 230 Korean patients with healthy livers. The proposed model was cross validated using a different data set of 37 patients with healthy livers. The total liver volume (TLV), except for the volume of liver blood vessels, was measured through computed tomography volumetry as the dependent variable. Various anthropometric variables, liver height (LH), thoracic width (TW), age, and sex (0, female and 1, male) were considered as candidates for independent variables. We conducted stepwise regression analysis to identify variables to be included in the proposed model.
Precise estimation of the standard liver volume (SLV) is crucial in decision making regarding major hepatectomy and living donor liver transplantation. A small-for-size graft with the ratio of graft weight to SLV <30%–40% [123] can cause small-for-size syndrome [4567891011]. Most SLV estimation formulas [121314151617181920] were developed based on anthropometric parameters, including body weight (BW), body height (BH), and body surface area (BSA), as well as age and sex. We previously evaluated these formulas and found that the mean percentage absolute differences of SLV estimation ranged from 12.9% to 28.3% [21]. Therefore, there is a need for more accurate SLV estimation formulas.
Recent studies have explored several new variables for SLV estimation formulas. Kokudo et al. [22] introduced thoracic width (TW) together with age and race (1, Asian and 0, Caucasian) to estimate SLV without using the BW. We previously proposed SLV estimation using body composition parameters, including body fat percentage (BFP) and abdominal fat percentage (AFP), as well as abdominal geometry parameters such as waist circumference (WC) and subcutaneous fat area (SFA), together with age, sex, and BW [21]. The mean percentage absolute differences of SLV estimation using our formula and that proposed by Kokudo et al. [22] were 9.6% and 13.0%, respectively. Although this formula achieved better accuracy, measurement of WC and SFA is cumbersome. Therefore, there is a need for a more efficient and accurate formula. Accordingly, this study aimed to develop an accurate and efficient formula for SLV estimation.
The present study protocol was approved by the Institutional Review Board at Jeonbuk National University Hospital (No. 2021-11-048). The informed consents from patients have been exempted.
We included 267 patients, including 88 female and 179 male patients (age, 51.9 ± 10.5 years [range, 30–79 years]), with healthy livers at Jeonbuk National University Hospital from January 2009 to December 2013. Among them, 230 patients (74 female and 156 male patients; mean age, 52.0 ± 10.8 years [range, 30–79 years]) were randomly selected for regression model creation and 37 patients (14 female and 23 male patients; mean age, 51.5 ± 8.9 years [range, 39–77 years]) for cross validation. The total liver volume (TLV) of each case was calculated from abdominal CT scans. TW (cm) was calculated as the distance between the left and right costophrenic angle using a scout image obtained during a CT scan [22], as shown in Fig. 1. We calculated the BSA using Du Bois et al.’s equation [23] which is BSA (m2) = BW (kg)0.425 × BH (cm)0.725 × 0.007184 [23] and body mass index (BMI) as BW divided by height squared (m2). Liver height (LH, mm) was defined as the absolute difference between the z-coordinates of the top and bottom CT slices containing the liver region, which was measured using the Medical Imaging Interaction Toolkit [24], as shown in Fig. 2.
CT images were obtained using a 128-row multidetector CT scanner SOMATOM Definition AS+ (Siemens, Forchheim, Germany). Potential liver donors fasted for >6 hours before CT scanning. CT scanning was performed with the donors holding their breath at the end of inspiration. After obtaining CT images without a contrast medium, 120–130 mL of iopromide (Ultravist 370, Schering, Berlin, Germany) was administered at a flow rate of 3 mL/s using a mechanical injector, followed by triphasic CT scanning during the arterial, portal, and delayed phases. We used an automatic bolus-tracking system CARE Bolus (Siemens) to trigger data acquisition after the descending aorta enhancement reached a threshold of 100 Hounsfield units. The scanning and reconstitution parameters were as follows: detector collimation = 128 × 1.5 mm for unenhanced scanning and 128 × 0.75 mm for enhanced scanning; pitch value (table feed per gantry rotation divided by collimated beam width) = 0.6; gantry rotation time = 0.5 sec; and slice thickness = 3 mm.
The TLV was calculated from abdominal CT scans in the delayed phase using the liver segmentation and volumetry functions of Dr. Liver (Humanopia, Inc., Pohang, Korea). The liver was semiautomatically segmented (Fig. 3) by picking up a set of seed points from different CT slides in Dr. Liver. Liver blood vessels, including the portal and hepatic veins, were excluded while calculating the TLV. The TLV was calculated using the summation-of-area method [25].
TLV was used as dependent variable to create a regression model for SLV prediction. We explored the following independent variables: age, sex (0, female and 1, male), BW, BH, BSA, BMI, TW, and LH. Stepwise regression was performed to determine the variables to be included in the regression model. The adequacy of fit of the regression model was assessed through residual analysis. Statistical analyses were conducted using Minitab ver. 18 (Minitab, Inc., State College, PA, USA) at a significance level of 0.05.
The created regression model was compared to the existing SLV estimation formulas. To compare with Yang et al.’s model [21], we measured the BFP, AFP, WC, and SFA of each case. The measures for evaluation included adjusted R2, absolute error (AE, mL) between the estimated SLV and actual TLV, percentage of AE (PAE), and percentage of cases with PAE of >20%. The paired t-test was conducted to identify significant differences between the estimated SLV calculated using different SLV estimation formulas and the actual TLV in Minitab at a significance level of 0.05.
We developed the following regression equation for SLV estimation: SLV = −1,275 + 9.85 × BW (kg) + 19.95 × TW (cm) + 7.401 × LH (mm). The model achieved 0.76 for adjusted R2, 141.3 mL for root mean square error (RMSE), 105.9 ± 72.6 mL for AE, 10.2% ± 7.5% for PAE, and 10.8% (4 out of 37 cases) for percentage of cases with PAE of >20%.
The created SLV estimation formula showed the best performance among existing formulas on the cross-validation data set. As shown in Table 1, the performance of the created formula (adjusted R2 = 0.76, RMSE = 141.3 mL, mean AE = 105.9 mL, mean PAE = 10.2%, percentage of PAE >20% = 10.8%) was highest among existing formulas (adjusted R2 = 0.30–0.96, RMSE = 171.8–367.3 mL, mean AE = 135.2–401.2 mL, mean PAE = 13.0%–40.0%, percentage of PAE >20% = 21.6%–81.1%).
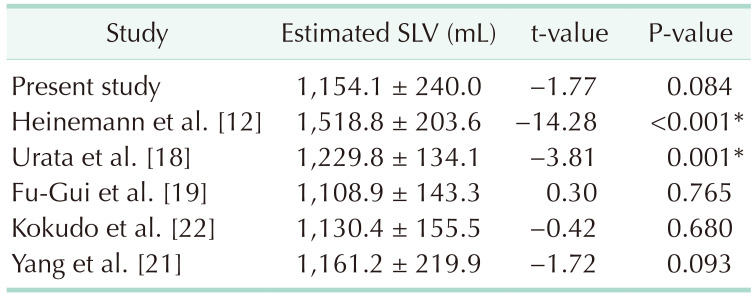
As shown in Table 2, the paired t-test showed that the estimated SLV calculated using our proposed formula or those described by Fu-Gui et al. [19], Kokudo et al. [22], or our previous study [21] did not significantly differ from the actual TLV on the cross-validation data set. The SLV estimated by the remaining formulas significantly differed from the actual TLV.
We created a formula for SLV estimation using demographic and anthropometric variables (age, sex, BW, BH, BSA, and BMI), TW, and LH for Korean healthy adults with normal livers. BW, TW, and LH were included in the created formula using stepwise regression analysis. This is the first report to include LH as a variable for SLV estimation. Our findings demonstrated that applying LH as a variable greatly improved the precision of the SLV estimation formula. Specifically, it improved the accuracy by 30–296 mL for AE, 2.8%–29.8% for PAE, and 10.8%–70.3% for percentage of PAE >20% compared with existing formulas.
Our proposed formula outperformed previously published formulas. It was developed based on CT volumetry, Korean population, and TLV excluding the liver blood volume. Furthermore, LH was introduced into the formula for the first time. Among the existing formulas, the formulas developed by Heinemann et al. [12] and Yu et al. [13] showed the largest error. This is because, in these studies, TLV was measured based on autopsy study without excluding structures attached to the liver, including the gallbladder, ligaments, and vessels [1521]. The remaining studies were based on CT volumetry. Among the remaining formulas, the formulas developed by Vauthey et al. [14] and Poovathumkadavil et al. [15] tended to have larger errors. This could be attributed to the race factor. Specifically, Vauthey et al.’s formula [14] was based on the North American and European populations while Poovathumkadavil et al.’s formula [15] was based on the Saudi Arabian population. The remaining formulas were based on the Asian population (Japan, Korean, or Chinese). Among the remaining formulas, formulas created based on the TLV, including the liver blood volume (Yuan et al.’s [16], Hashimoto and Makuuchi’s [17], and Urata et al.’s [18], except Um et al.’s [20]), had larger error than those developed based on TLV excluding the liver blood volume. Kokudo et al. [22] were the first to introduce the TW to the SLV estimation formula. Cross validation in our study showed that their formula was ranked third, which indicated that the TW is a good variable for SLV estimation. TW was also selected in our study based on stepwise regression analysis. Yang et al.’s formula [21] showed the closest performance to our proposed formula. However, their formula included 7 variables, which is cumbersome for clinical application. Contrastingly, our formula only included 3 variables. Further, TW and LH measurement are quite simple. Therefore, our formula is more efficient than Yang et al.’s formula [21].
We did not include age in our proposed formula. Most existing formulas did not contain age; further, these previous studies mainly included young people [2122]. The formulas developed by Kokudo et al. [22] and Yang et al. [21] included age. Kokudo et al. [22] reported that the difference in the SLV between healthy adults in their 20s and 80s can be as large as 200 mL. However, we observed no association between age and the TLV. Pearson correlation analysis revealed a weak correlation of age and the TLV (r [228] = −0.269, P < 0.001). Yang et al.’s formula [21] also included sex. Our findings demonstrated a moderate correlation of sex with TLV (r [228] = 0.478, P < 0.001).
In Table 2, some formulas including Fu-Gui et al.’s [19], Kokudo et al.’s [22], and Yang et al.’s [21] seem to be more accurate to estimate SLV than the proposed formula, but not statistically significant. However, in terms of AE, the new formula is mostly preferred. The results in Table 1 have shown that the proposed new formula outperformed other formulas in terms of adjusted R2, RMSE, AE, PAE, and percentage of PAE >20%. The present study was limited by the relatively small size of the cross-validation set. In the future study, we will include more cases to generalize the findings of the present study.
The present study does have another limitation. In clinical practice of living donor liver transplantation, most recipients have cirrhotic liver, in which case their liver sizes and therefore LHs tend to be relatively small at the time of diagnosis compared to the time when they were healthy. The more severe the degree of cirrhosis, the more the LH decreases. Since our formula uses the height of healthy liver to estimate SLV, the clinical application of our formula is limited to the cases with nearly normal-sized liver, such as mild cirrhosis. For the cases with significant decrease of liver size that is visible to the naked eye, such as severe cirrhosis, the proposed formula is likely to be inapplicable due to the decrease of LH. To overcome the limitation of our formula, we need to analyze the effect of cirrhosis on LH, find an adjustment factor to LH based on the severity level of cirrhosis, and apply that adjustment factor to our formula in future work.
In conclusion, this study proposed a new formula for SLV estimation based on BW, TW, and LH. The new formula predicted the TLV on the cross-validation data set more precisely than existing formulas. Our formula can be used in the Asian population for SLV estimation.
Notes
References
1. Lo CM, Fan ST, Liu CL, Chan JK, Lam BK, Lau GK, et al. Minimum graft size for successful living donor liver transplantation. Transplantation. 1999; 68:1112–1116. PMID: 10551638.

2. Chen CL, Fan ST, Lee SG, Makuuchi M, Tanaka K. Living-donor liver transplantation: 12 years of experience in Asia. Transplantation. 2003; 75(3 Suppl):S6–S11. PMID: 12589130.

3. Kawasaki S, Makuuchi M, Matsunami H, Hashikura Y, Ikegami T, Nakazawa Y, et al. Living related liver transplantation in adults. Ann Surg. 1998; 227:269–274. PMID: 9488526.

4. Kiuchi T, Kasahara M, Uryuhara K, Inomata Y, Uemoto S, Asonuma K, et al. Impact of graft size mismatching on graft prognosis in liver transplantation from living donors. Transplantation. 1999; 67:321–327. PMID: 10075602.

5. Sugawara Y, Makuuchi M, Takayama T, Imamura H, Dowaki S, Mizuta K, et al. Small-for-size grafts in living-related liver transplantation. J Am Coll Surg. 2001; 192:510–513. PMID: 11294408.

6. Inomata Y, Kiuchi T, Kim I, Uemoto S, Egawa H, Asonuma K, et al. Auxiliary partial orthotopic living donor liver transplantation as an aid for small-for-size grafts in larger recipients. Transplantation. 1999; 67:1314–1319. PMID: 10360583.

7. Ben-Haim M, Emre S, Fishbein TM, Sheiner PA, Bodian CA, Kim-Schluger L, et al. Critical graft size in adult-to-adult living donor liver transplantation: impact of the recipient’s disease. Liver Transpl. 2001; 7:948–953. PMID: 11699030.

8. Heaton N. Small-for-size liver syndrome after auxiliary and split liver transplantation: donor selection. Liver Transpl. 2003; 9:S26–S28. PMID: 12942475.

9. Sakamoto S, Uemoto S, Uryuhara K, Kim Id, Kiuchi T, Egawa H, et al. Graft size assessment and analysis of donors for living donor liver transplantation using right lobe. Transplantation. 2001; 71:1407–1413. PMID: 11391227.

10. Nishizaki T, Ikegami T, Hiroshige S, Hashimoto K, Uchiyama H, Yoshizumi T, et al. Small graft for living donor liver transplantation. Ann Surg. 2001; 233:575–580. PMID: 11303141.

11. Kiuchi T, Tanaka K, Ito T, Oike F, Ogura Y, Fujimoto Y, et al. Small-for-size graft in living donor liver transplantation: how far should we go? Liver Transpl. 2003; 9:S29–S35.

12. Heinemann A, Wischhusen F, Püschel K, Rogiers X. Standard liver volume in the Caucasian population. Liver Transpl Surg. 1999; 5:366–368. PMID: 10477836.

13. Yu HC, You H, Lee H, Jin ZW, Moon JI, Cho BH. Estimation of standard liver volume for liver transplantation in the Korean population. Liver Transpl. 2004; 10:779–783. PMID: 15162473.

14. Vauthey JN, Abdalla EK, Doherty DA, Gertsch P, Fenstermacher MJ, Loyer EM, et al. Body surface area and body weight predict total liver volume in Western adults. Liver Transpl. 2002; 8:233–240. PMID: 11910568.

15. Poovathumkadavil A, Leung KF, Al Ghamdi HM, Othman Iel H, Meshikhes AW. Standard formula for liver volume in Middle Eastern Arabic adults. Transplant Proc. 2010; 42:3600–3605. PMID: 21094823.

16. Yuan D, Lu T, Wei YG, Li B, Yan LN, Zeng Y, et al. Estimation of standard liver volume for liver transplantation in the Chinese population. Transplant Proc. 2008; 40:3536–3540. PMID: 19100432.

17. Hashimoto T, Makuuchi M. Transplantation: Liver steatosis and errors in estimation of standard liver volume. Nat Rev Gastroenterol Hepatol. 2011; 8:667–668. PMID: 22083115.

18. Urata K, Kawasaki S, Matsunami H, Hashikura Y, Ikegami T, Ishizone S, et al. Calculation of child and adult standard liver volume for liver transplantation. Hepatology. 1995; 21:1317–1321. PMID: 7737637.

19. Fu-Gui L, Lu-Nan Y, Bo L, Yong Z, Tian-Fu W, Ming-Qing X, et al. Estimation of standard liver volume in Chinese adult living donors. Transplant Proc. 2009; 41:4052–4056. PMID: 20005340.

20. Um EH, Hwang S, Song GW, Jung DH, Ahn CS, Kim KH, et al. Calculation of standard liver volume in Korean adults with analysis of confounding variables. Korean J Hepatobiliary Pancreat Surg. 2015; 19:133–138. PMID: 26693231.

21. Yang X, Yang JD, Lee S, Hwang HP, Ahn S, Yu HC, et al. Estimation of standard liver volume using CT volume, body composition, and abdominal geometry measurements. Yonsei Med J. 2018; 59:546–553. PMID: 29749138.

22. Kokudo T, Hasegawa K, Uldry E, Matsuyama Y, Kaneko J, Akamatsu N, et al. A new formula for calculating standard liver volume for living donor liver transplantation without using body weight. J Hepatol. 2015; 63:848–854. PMID: 26057995.

23. Du Bois D, Du Bois EF. A formula to estimate the approximate surface area if height and weight be known. 1916. Nutrition. 1989; 5:303–313. PMID: 2520314.
24. Nolden M, Zelzer S, Seitel A, Wald D, Müller M, Franz AM, et al. The Medical Imaging Interaction Toolkit: challenges and advances: 10 years of open-source development. Int J Comput Assist Radiol Surg. 2013; 8:607–620. PMID: 23588509.
25. Heymsfield SB, Fulenwider T, Nordlinger B, Barlow R, Sones P, Kutner M. Accurate measurement of liver, kidney, and spleen volume and mass by computerized axial tomography. Ann Intern Med. 1979; 90:185–187. PMID: 443650.

Fig. 1
Measurement of thoracic width (arrow) as the distance between the left and right costophrenic angle using a scout image obtained during a CT scan.
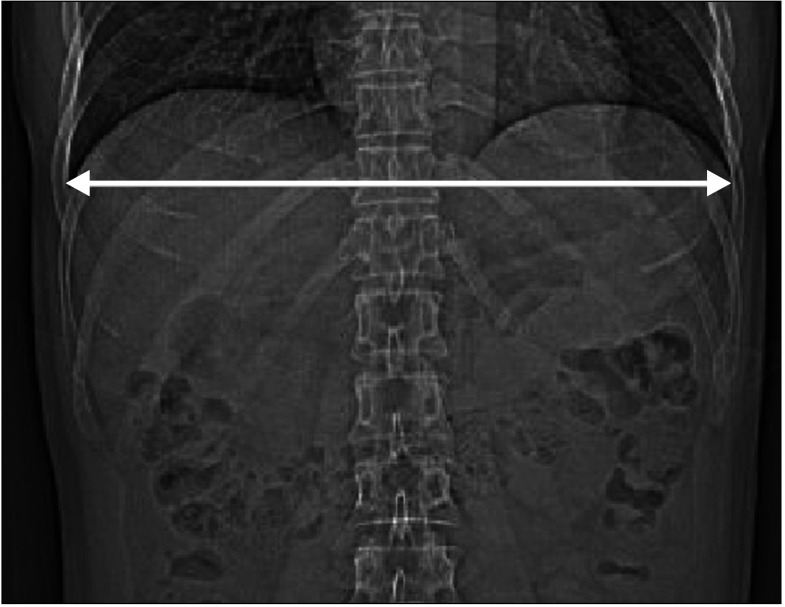
Fig. 2
Measurement of liver height as the absolute difference between the z-coordinates of the top (A) and bottom (B) CT slices containing the liver region using the Medical Imaging Interaction Toolkit [24]. 3D, 3 dimensional.
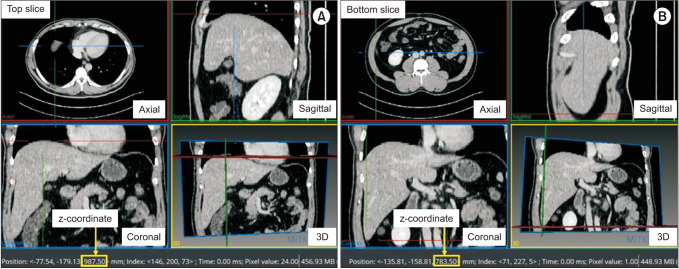
Fig. 3
Liver segmentation for liver volumetry by Dr. Liver (Humanopia, Inc., Pohang, Korea). 3D, 3 dimensional.
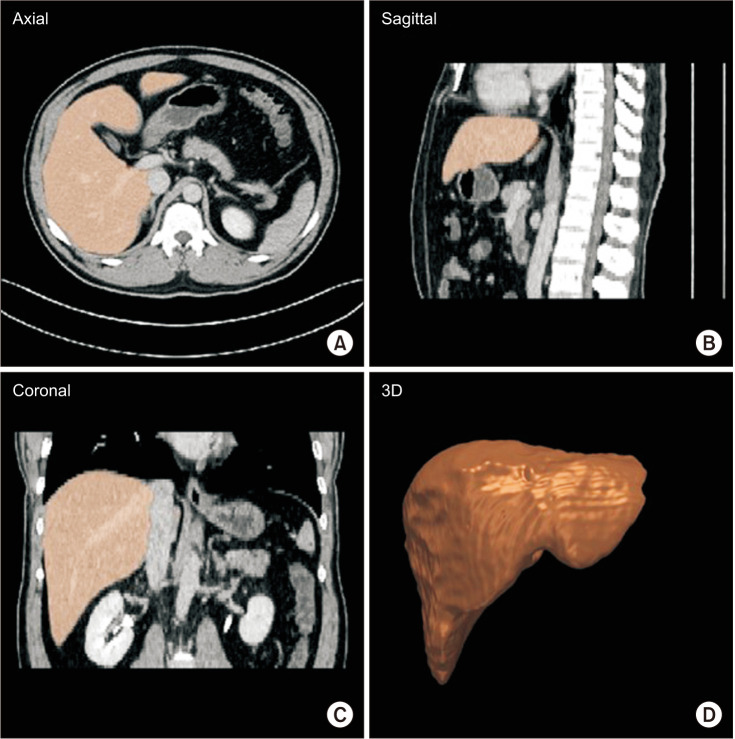
Table 1
Comparison of the existing formulas and new formulas for SLV estimation using a cross-validation data set of n = 37
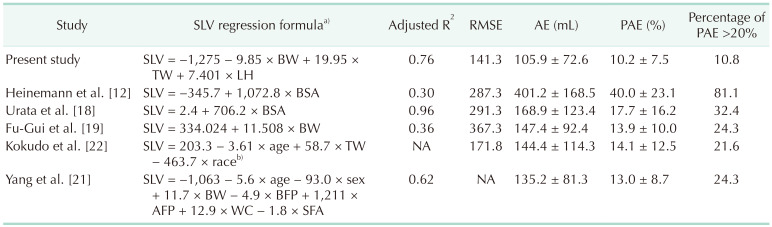
Values are presented as data only or mean ± standard deviation.
SLV, standard liver volume; RMSE, root mean square error; AE, absolute error; PAE, percentage of AE; BW, body weight; TW, thoracic width; LH, liver height; BSA, body surface area; BFP, body fat percentage; AFP, abdominal fat percentage; WC, waist circumference; SFA, subcutaneous fat area; NA, not available.
a)Sex: female, 0 and male, 1. b)Race: 1, Asian and 0, Caucasian.




 PDF
PDF Citation
Citation Print
Print



 XML Download
XML Download