Abstract
Stature estimation is an important process of biological profile analysis for the identification of skeletal remains. In forensic practice, non-long bones might be needed for estimating stature, in case long bones were not recovered or well preserved. This study developed the stature estimation model from dry sterna in a Thai population. The combined length of manubrium and mesosternum (CMM) was the best single stature estimation indicator for males and combined sex samples, whereas the sternal area (SA) was the best stature estimation indicator for females in our study. The best multiple regression analysis models of our study were stature equal 122.685+0.182 (CMM)+0.592 (intercostal length between the third and fourth ribs [ICL34]) with a standard error of estimation (SEE) of 6.134 cm for males, stature equal 130.676+0.005 (SA) with SEE of 5.370 cm for females, and stature equal 79.412+0.342 (CMM)+0.506 (corpus sterni width at first sternebra [CSWS1])+0.794 (ICL34) with SEE of 6.222 cm for unknown sex samples. The results indicated that a sternum can be used for estimating the stature of skeletal remains in a Thai population. However, these models might not be suitable for other populations, especially, in case the suspected stature is over the stature range in our study.
Personal identification is an important process of a legal proceeding. Without definite personal identification, the criminal and civil proceedings related to the deceased will be delayed. According to disaster victim identification guidelines of Interpol, DNA, fingerprints, and dental profiles are the primary criteria of victims’ identification and only one matching method is enough for definite identification [1]. However, these methods need the antemortem data of possible missing persons before matching with the unknown deceased.
Biological profiles of the deceased, which consist of ancestry, age, sex, and stature, are valuable data that assist to narrow down the number of possible missing persons. Stature is a valuable piece of biological profile information, that may provide a valuable clue of the personal identification process when the unknown deceased or missing person is tall or short in their population [2]. The method of stature estimation from skeletal remains can be classified into two categories. The first is an anatomical method which uses the summation lengths of the bones that are the main composite of body height to calculate the stature. The second is a mathematical method which calculates the stature from the length of the one or more pieces of bones. The anatomical method indicates the higher accuracy of stature estimation than those of the mathematical method, but requires the complete skeletal remains to estimate the stature [3]. By the limitations of the anatomical method, the mathematical method might be more suitable for forensic cases, in which the complete skeletal remains are not usually recovered.
The long bones were recommended for estimating the stature of the skeletal remains. Previous reports indicated femur, tibia, fibular, humerus, radius, or ulnar could predict the stature of the skeletal remains with a high rate of accuracy [4-8]. However, variations of bone length and stature, and stature estimation models exist between populations. A stature estimation model generated from one population might not be proper to use with another population [2, 3]. Thus, a specific stature estimation of each population is required.
In 2011, Mahakkanukrauh et al. [5], reported a highly accurate stature estimation model in a Thai population by using the long bone lengths. The correlation coefficient of bone length and height ranged from 0.660 to 0.769, and the stature estimation model using fibular length provided the lowest standard error of estimation (SEE) as 4.59 cm in male samples. In the female samples, the femur provided the lowest SEE as 5.21 cm among the stature estimation model, and the correlation coefficient bone length and height ranged from 0.552 to 0.762. However, in situations such as mass disasters, terrorist attacks, and plane crashes, long bones might not be recovered or may be damaged, and cannot be used for estimating heights. Therefore, stature estimation using other bones instead of long bones is still needed. In addition, in the cases of dismemberment with only the thorax recovered, stature estimation of the remains using the sternum might be necessary.
Previous studies reported a significant correlation between sternal dimension and height. Saraf et al. [9] reported a high correlation between sternal dimension with height with a SEE of fewer than three centimeters in Mysore India (South India) population. However, discrepancies in the results of studies in Portuguese, Spanish, Central, and Northern Indian samples indicated a low correlation between sternal dimension and height [10-13]. These demonstrated variations of the relationship between sternal dimension and height among populations.
To our knowledge, no report of stature estimation model using sternal dimension is reported in the Thai population. This piece of information might be necessary in case the long bone of the skeletal remains was not recovered. Therefore, this study aimed to generate a stature estimation model using the sternal dimension in a Thai population.
The 219 sterna were divided into 199 sterna (male 104, female 95), for the training sample and 20 sterna for the test sample (male 10, female 10), were derived from the Osteology Research and Training Center, Faculty of Medicine, Chiang Mai University, Thailand. The samples were derived from donated bodies, which are Thai who lived in the Northern Thai area and died between 2006 and 2019. The mean age of training samples was 66.5 years and a standard deviation of 14.4 years (males, 66.47±14.20 years; females, 66.59±14.78 years). The age range was from 26 to 94 years because the epiphyseal closure process occurs between 16 and 25 years old affecting the bone-lengthening process. Therefore the ages of samples lower than 25 years were not included in this study. In addition, the samples that demonstrated anomalies, congenital or acquired deformities affecting measurements were also excluded. The mean age of the test samples was 66.80 years with 14.54 years of standard deviation (males, 62.10±5.82 years; females, 71.50±3.43 years), and the age range was from 45 to 94 years.
The length of the cadaver was measured from the vertex of the head to the heel of the foot with the cadaver in a supine position before skeletal processing then all of the sternums were macerated and allowed to dry. The range of cadaver length of training samples was between 140 to 180 cm. with the mean and the standard deviation of cadaver length of 159.51±9.518 cm (males, 166.19±116.7 cm; females, 152.2±10.87 cm). The range of cadaver length of the test sample was between 145 to 175 cm with the mean and the standard deviation of cadaver length of 159.7±7.83 cm (males, 166.19±6.83 cm; females, 152.2±6.017 cm).
The study was approved by the ethical committee of the Faculty of medicine, Chiang Mai University (FOR-2564-08394). The informed consent was waived.
The sternal dimensions were measured by using digital vernier calipers in millimeters by one of the researchers (VJ), and 20 sterna were randomly chosen from the training sample to repeat measurements by VJ and WK to test the intra and inter-observer agreement. The details of the measurements were demonstrated in Table 1 and Fig. 1 [14, 15].
The data were analyzed using IBM SPSS software version 22 (IBM Corp., Armonk, NY, USA). The observer agreement was tested by the technical error of measurement, and an independent t-test was performed to compare the difference in height, age, and sternal dimensions between the sexes. Karl Pearson’s correlation was analyzed to observe the correlation between stature and sternal dimension. Regression analysis was performed to generate the stature estimation model, and the constant of the model will be subtracted 2 cm to refer to the living stature, in which 2 cm is generally accepted to subtract from cadaver length to approximate living stature [4, 5, 16]. To test the accuracy of stature estimation equations, the equations were applied to test samples, and the mean percent error to the corrected stature and percent of accuracy within the first SEE and 95% confident interval (CI) were calculated. The P-value of less than 0.05 was considered statistically significant.
There was no significant statistical difference of age between male and female samples (P=0.94), however, the average cadaver length of male samples was significantly higher than those of female samples at 12.4 cm (P<0.01). The relative technical error of measurement of all measurements was less than 1.5 for intra-observation error and less than 2 for inter observation error, which was the acceptable range [17], and the R-value of all measurements was more than 0.9. These results indicated the measurements in this study were reliable.
Sternal dimension and index of males were significantly larger than those of females, except sternal index (Table 2), and the correlation between stature and all sternal measurements were shown in Table 3. The majority of sternal measurements indicated a significant positive correlation with stature, except sternal index in the combined sex samples. The combined length of manubrium and mesosternum (CMM) indicated the highest correlation with stature, followed by sternal area (SA) and mesosternum length (MSL). In the male samples, CMM also demonstrated the highest correlation with stature, and intercostal 3rd–4th (ICL34) and MSL were second and third, respectively. Intercostal 2nd–3rd (ICL23) and SA also statistically correlated with stature, but other parameters were not correlated in male samples. For the female samples, SA was the best stature correlated parameter, and CMM and MSL were in the second and third place, respectively. Manubrium length (MBL), manubrium width (MBW), ICL23, and corpus sterni width at the third sternebra (CSWS3) were also significantly correlated with stature (Table 3).
The simple regression analysis model for male, female, and combined samples was shown in Table 4 and Fig. 2. The stature estimation model of the male sample demonstrated a higher correlation and lower SEE than those of the male sample. The coefficient of determination (R2) and SEE of female’s stature estimation model ranged from 0.060 to 0.204 and 5.370 to 5.829 cm, respectively, whereas the R2 male samples were ranged from 0.062 to 0.167 and 6.240 to 6.618 cm. for SEE. The stature estimation model generated from combined male and female samples increased the R2 value (0.072–0.514) but did not improve the SEE of the model (6.636–9.169 cm).
The stepwise multiple regression models acquired for stature estimation from sternal measurements provided superior correlation than those of simple linear regression in unknown sex and males but did not improve the accuracy for females (Table 5). The CMM, CSWS1, and ICL34 were selected for the stature estimation model for unknown sex samples, and CMM and ICL34 were also selected for the male’s stature estimation model. On the other hand, SA was the only variable that was selected for the female stature estimation model.
The multiple regression equations were applied to the test samples (Table 6). The female-specific equation demonstrated the highest mean percent error to the corrected stature than those of males and the combined sex’s equation. The mean percent error to the corrected stature of the female-specific equation was 3.81%, whereas the mean percent error to the corrected stature of the male and combined sex’s equation ranged from 2.58% to 3.46%. However, the predicted stature using multiple regression equations of all test samples were in the range of first SEE and 95% CI.
Stature estimation is an important process of biological profile analysis to identification of the skeletal remain. Long bones have proved to be a useful indicator for estimating stature, however, in routine forensic practice, the long bone might not be recovered or well-preserved enough to use as stature estimation tools. Therefore, stature estimation using non-long bones is still necessary. The results of our study indicated the sternum can be used for estimating the stature of skeletal remains in a Thai population. The stature estimation models of our study can estimate the stature with SEE of 6.134 cm for males, 5.370 cm for females, and 6.222 cm for unknown sex samples.
Previous studies of stature estimation using sternum dimension indicated different levels of accuracy results. In 2018, Saraf et al. [9] reported the stature estimation models using sternal dimensions can estimate the stature with the coefficient of determination (R2) was more than 0.75 and the SEE was less than 2 cm, in Mysore India (south India) population. The study of stature estimation in Turkish and other South Indian populations indicated the sternal dimension can estimate the stature with the highest R2 of 0.640 and 0.408, and the lowest SEE of 3.1 cm and 4.11 cm, respectively [18-20]. However, the highest R2 of stature estimation model using sternal dimensions in Central Indian, Portuguese, Spanish and Western Chinese were not more than 0.302 and the lowest SEE was not less than 4.76 cm [10, 11, 13, 21]. The results of the latter studies were consistent with our results that the highest R2 was 0.204 and the lowest SEE was 5.37 cm (Table 7). The discrepancy of the results of our study and others might be from the difference in, population, genetics, nutrition, demographics, and so on. These factors affect the bone dimension and the stature of each population [22, 23]. Moreover, the difference between the type of sample such as fresh or dry skeleton, and the age and height distribution of the samples might also affect the accuracy of the results.
The CMM was the best predictive measurement for stature estimation of male and combined sex samples in our study. This result was according to previous studies [9, 12, 13, 20], however, the accuracy of the stature estimation model was different between populations. The correlation coefficient and determination of stature estimation model of males in our study were higher than those of Spanish and Northern Indian population but lower than those of South Indian, Central Indian, Turkish, and Western Chinese populations [9-13, 18, 20, 21]. The R and R2 of the male’s stature estimation model, the R and R2 of the combined sex estimation model were also better than those of the Northern Indian population but lower than those of the South Indian and Turkish populations [9, 12, 20]. Although CMM was not the predictive measurement for stature estimation of the female sample in our study the R and R2 of the female’s stature estimation model was close to those of our male sample and also better than those of the Northern Indian population [12].
Interestingly, the SA indicated the best measurement for stature estimation of female samples and was in the second place for combined sex samples, however, the SA did not demonstrate superior results in male samples. This might be explained by the significant difference between male and female SA [15]. However, the reason that the female stature estimation model was better than those of males was unknown. In addition, no previous reports were found for using the SA to estimate the stature for comparing the results.
Not only CMM and SA but also MSL could be used for stature estimation in the Thai population. The R and R2 of stature estimation model was the third range in male, female, and combined sex samples . In addition, the R and R2 of stature estimation model using MSL of our study was greater than those of Northern and Central Indian populations but inferior to those of South Indian and Turkish populations [9, 12, 13, 20].
The R and R2 of the combined sex samples in this study were greater than those of the sex-specific model but the SEE was higher than those of the sex-specific model. This might be the effect of statistical artifacts, which combine sex samples increased the stature and measurement range. Increasing the range of variables can lead to a “range enhancement” effect, with a possiblity to increase the mean [5, 24]. Thus, the result of the combined sex sample should not indicate greater accuracy than those of sex-specific samples.
Even though the accuracy of stature estimation using sternal dimension in a Thai population of our study was inferior to those of long bones which can be estimated the stature with highest R of 0.783 and 0.785, and lowest SEE was 4.95 cm and 5.10 cm, for males and females respectively [5]. However, when comparing with the stature estimation model using non-long bones in the Thai population, stature estimation using the sternum was better than those of the skull and mandible but inferior to those of vertebral columns, calcaneus, and talus [25-27]. The stature estimation using vertebral column showed best R was 0.725 and lowest SEE was 5.796 cm [25], the calcaneus and talus showed highest R in male and female was 0.63 and 0.54 and lowest SEE was 5.95 and 3.06 cm, respectively [26], whereas the stature estimation using the skull and mandible dimension indicated the highest R was 0.403 and 0.709 and the lowest SEE was 7.319 cm and 6.216 cm, for males and females, respectively.
Despite limitations of using sternum as stature estimation tools, in situations such as dismemberment remains with only the thorax recovered, the sternum might be a valuable tool for stature estimation or used as adjuvant to estimate stature with another bone. In addition, the recovery rate of the sternum was higher than those of the calcaneus and talus [28]. Thus, the sternum can be used for stature estimation in a situation where the long bone was not recovered, damaged, or used as an adjuvant tool for stature estimation of skeletal remains.
The limitations of our study were the range of cadaver lengths in males and females of our samples of 150–180 cm, 140–167 cm, respectively. That means stature estimation in a different population or different range of height could be used with consideration. For this reason, further study was suggested in different populations in the future.
Acknowledgements
The authors sincerely appreciate and pay great respect to the individuals and families who donated bodies and skeletons to the Faculty of Medicine for medical research. Moreover, the authors would like to thank the support from the Forensic Osteology Research Center, Faculty of Medicine, Chiang Mai University, and partial support from Chiang Mai University. This study was supported by the Faculty of Medicine, Chiang Mai University.
Notes
References
1. INTERPOL. 2018. INTERPOL disaster victim identification guide [Internet]. INTERPOL;Lyon: Available from: https://www.interpol.int/content/download/589/file/18Y1344%20E%20DVI_Guide.pdf. cited 2021 Dec 15.
2. Christensen AM, Passalacqua NV, Bartelink EJ. 2019. Forensic anthropology current methods and practice. 2nd ed. Academic Press;London: DOI: 10.1016/B978-0-12-815734-3.00001-4.
3. DiGangi EA, Moore MK. 2012. Research methods in human skeletal biology. Academic Press;London: DOI: 10.1016/B978-0-12-385189-5.00018-2.
4. De Mendonça MC. 2000; Estimation of height from the length of long bones in a Portuguese adult population. Am J Phys Anthropol. 112:39–48. DOI: 10.1002/(SICI)1096-8644(200005)112:1<39::AID-AJPA5>3.0.CO;2-#. PMID: 10766942.

5. Mahakkanukrauh P, Khanpetch P, Prasitwattanseree S, Vichairat K, Troy Case D. 2011; Stature estimation from long bone lengths in a Thai population. Forensic Sci Int. 210:279.e1–7. DOI: 10.1016/j.forsciint.2011.04.025. PMID: 21616616.

6. Muñoz JI, Liñares-Iglesias M, Suárez-Peñaranda JM, Mayo M, Miguéns X, Rodríguez-Calvo MS, Concheiro L. 2001; Stature estimation from radiographically determined long bone length in a Spanish population sample. J Forensic Sci. 46:363–6. DOI: 10.1520/JFS14973J. PMID: 11305442.

7. Radoinova D, Tenekedjiev K, Yordanov Y. 2002; Stature estimation from long bone lengths in Bulgarians. Homo. 52:221–32. DOI: 10.1078/0018-442X-00030. PMID: 12018118.

8. Nath S, Badkur P. 2002; Reconstruction of stature from long bone lengths. Anthropologist. 4:109–14. DOI: 10.1080/09720073.2002.11890736.

9. Saraf A, Kanchan T, Krishan K, Ateriya N, Setia P. 2018; Estimation of stature from sternum - exploring the quadratic models. J Forensic Leg Med. 58:9–13. DOI: 10.1016/j.jflm.2018.04.004. PMID: 29679840.

10. Macaluso PJ Jr, Lucena J. 2014; Stature estimation from radiographic sternum length in a contemporary Spanish population. Int J Legal Med. 128:845–51. DOI: 10.1007/s00414-014-0975-3. PMID: 24526040.

11. Marinho L, Almeida D, Santos A, Cardoso HF. 2012; Is the length of the sternum reliable for estimating adult stature? A pilot study using fresh sterna and a test of two methods using dry sterna. Forensic Sci Int. 220:292.e1–4. DOI: 10.1016/j.forsciint.2012.02.012. PMID: 22421326.

12. Singh J, Pathak RK, Chavali KH. 2011; Skeletal height estimation from regression analysis of sternal lengths in a Northwest Indian population of Chandigarh region: a postmortem study. Forensic Sci Int. 206:211.e1–8. DOI: 10.1016/j.forsciint.2010.08.023. PMID: 20869826.

13. Tumram NK, Parchake SB, Bardale RV, Dixit PG. 2016; Estimation of height from the length of the sternum in an adult Indian population. Med Sci Law. 56:46–52. DOI: 10.1177/0025802415595057. PMID: 26209632.

14. Ashley GT. 1956; The human sternum: the influence of sex and age on its measurements. J Forensic Med. 3:27–43.
15. Macaluso PJ Jr. 2010; The efficacy of sternal measurements for sex estimation in South African blacks. Forensic Sci Int. 202:111.e1–7. DOI: 10.1016/j.forsciint.2010.07.019. PMID: 20696541.

16. Meadows L, Jantz RL. 1992; Estimation of stature from metacarpal lengths. J Forensic Sci. 37:147–54. DOI: 10.1520/JFS13222J. PMID: 1545195.

17. Perini TA, de Oliveira GL, Ornellas JdS, de Oliveira FP. 2005; Technical error of measurement in anthropometry. Rev Bras Med Esporte. 11:87–90. DOI: 10.1590/S1517-86922005000100009.
18. Menezes RG, Kanchan T, Kumar GP, Rao PP, Lobo SW, Uysal S, Krishan K, Kalthur SG, Nagesh KR, Shettigar S. 2009; Stature estimation from the length of the sternum in South Indian males: a preliminary study. J Forensic Leg Med. 16:441–3. DOI: 10.1016/j.jflm.2009.05.001. PMID: 19782312.

19. Menezes RG, Nagesh KR, Monteiro FN, Kumar GP, Kanchan T, Uysal S, Rao PP, Rastogi P, Lobo SW, Kalthur SG. 2011; Estimation of stature from the length of the sternum in South Indian females. J Forensic Leg Med. 18:242–5. DOI: 10.1016/j.jflm.2011.04.004. PMID: 21771553.

20. Yonguc GN, Kurtulus A, Bayazit O, Adiguzel E, Unal I, Demir S, Acar K. 2015; Estimation of stature and sex from sternal lengths: an autopsy study. Anat Sci Int. 90:89–96. DOI: 10.1007/s12565-014-0235-0. PMID: 24748542.

21. Zhang K, Luo YZ, Fan F, Zheng JQ, Yang M, Li T, Pang T, Zhang J, Deng ZH. 2015; Stature estimation from sternum length using computed tomography-volume rendering technique images of western Chinese. J Forensic Leg Med. 35:40–4. DOI: 10.1016/j.jflm.2015.07.003. PMID: 26344458.

22. Moro C, Covino J. 2018; Nutrition and growth: assessing the impact of regional nutritional intake on childhood development and metacarpal parameters. Anat Cell Biol. 51:31–40. DOI: 10.5115/acb.2018.51.1.31. PMID: 29644108. PMCID: PMC5890015.

23. Jelenkovic A, Sund R, Hur YM, Yokoyama Y, Hjelmborg JV, Möller S, Honda C, Magnusson PK, Pedersen NL, Ooki S, Aaltonen S, Stazi MA, Fagnani C, D'Ippolito C, Freitas DL, Maia JA, Ji F, Ning F, Pang Z, Rebato E, Busjahn A, Kandler C, Saudino KJ, Jang KL, Cozen W, Hwang AE, Mack TM, Gao W, Yu C, Li L, Corley RP, Huibregtse BM, Derom CA, Vlietinck RF, Loos RJ, Heikkilä K, Wardle J, Llewellyn CH, Fisher A, McAdams TA, Eley TC, Gregory AM, He M, Ding X, Bjerregaard-Andersen M, Beck-Nielsen H, Sodemann M, Tarnoki AD, Tarnoki DL, Knafo-Noam A, Mankuta D, Abramson L, Burt SA, Klump KL, Silberg JL, Eaves LJ, Maes HH, Krueger RF, McGue M, Pahlen S, Gatz M, Butler DA, Bartels M, van Beijsterveldt TC, Craig JM, Saffery R, Dubois L, Boivin M, Brendgen M, Dionne G, Vitaro F, Martin NG, Medland SE, Montgomery GW, Swan GE, Krasnow R, Tynelius P, Lichtenstein P, Haworth CM, Plomin R, Bayasgalan G, Narandalai D, Harden KP, Tucker-Drob EM, Spector T, Mangino M, Lachance G, Baker LA, Tuvblad C, Duncan GE, Buchwald D, Willemsen G, Skytthe A, Kyvik KO, Christensen K, Öncel SY, Aliev F, Rasmussen F, Goldberg JH, Sørensen TI, Boomsma DI, Kaprio J, Silventoinen K. 2016; Genetic and environmental influences on height from infancy to early adulthood: an individual-based pooled analysis of 45 twin cohorts. Sci Rep. 6:28496. DOI: 10.1038/srep28496. PMID: 27333805. PMCID: PMC4917845.

24. Alexander RA. 1988; Group homogeneity, range restriction, and range enhancement effects on correlations. Pers Psychol. 41:773–7. DOI: 10.1111/j.1744-6570.1988.tb00653.x.

25. Inchai C. 2016. Stature estimation from skull using craniometric method in a Thai population [thesis]. Chiang Mai University;Chiangmai: DOI: 10.1111/j.1744-6570.1988.tb00653.x.
26. Inchai C, Sinthubua A, Mahakkanukrauh P, Ruengdit S, Singsuwan P. 2019; Stature estimation from vertebral column in a Thai population. Int Med J. 26:213–5.
27. Scott S, Peckmann TR, Patriquin ML, Varas CG, Meek S. 2019; The estimation of stature from the tarsals: enhancing the disaster victim identification process in Thailand using the calcaneus and the talus. Forensic Anthropol. 2:332–46. DOI: 10.5744/fa.2019.1026.

28. Sorg MH, Haglund WD, Marden K. 2017. Forensic taphonomy: the postmortem fate of human remains. 2nd ed. CRC Press;Boca Raton: DOI: 10.5744/fa.2019.1026.
Fig. 1
Measurement on the sternum. MBL, manubrium length; MBW, manubrium width; MSL, mesosternum length; CMM, combined length of manubrium and mesosternum; ICL23, intercostal length between 2nd rib and 3rd rib; ICL34, intercostal length between 3rd rib and 4th rib; ICL45, intercostal length between 4th rib and 5th rib; CSWS1, corpus sterni width at first sternebra; CSWS3, corpus sterni width at third sternebra.
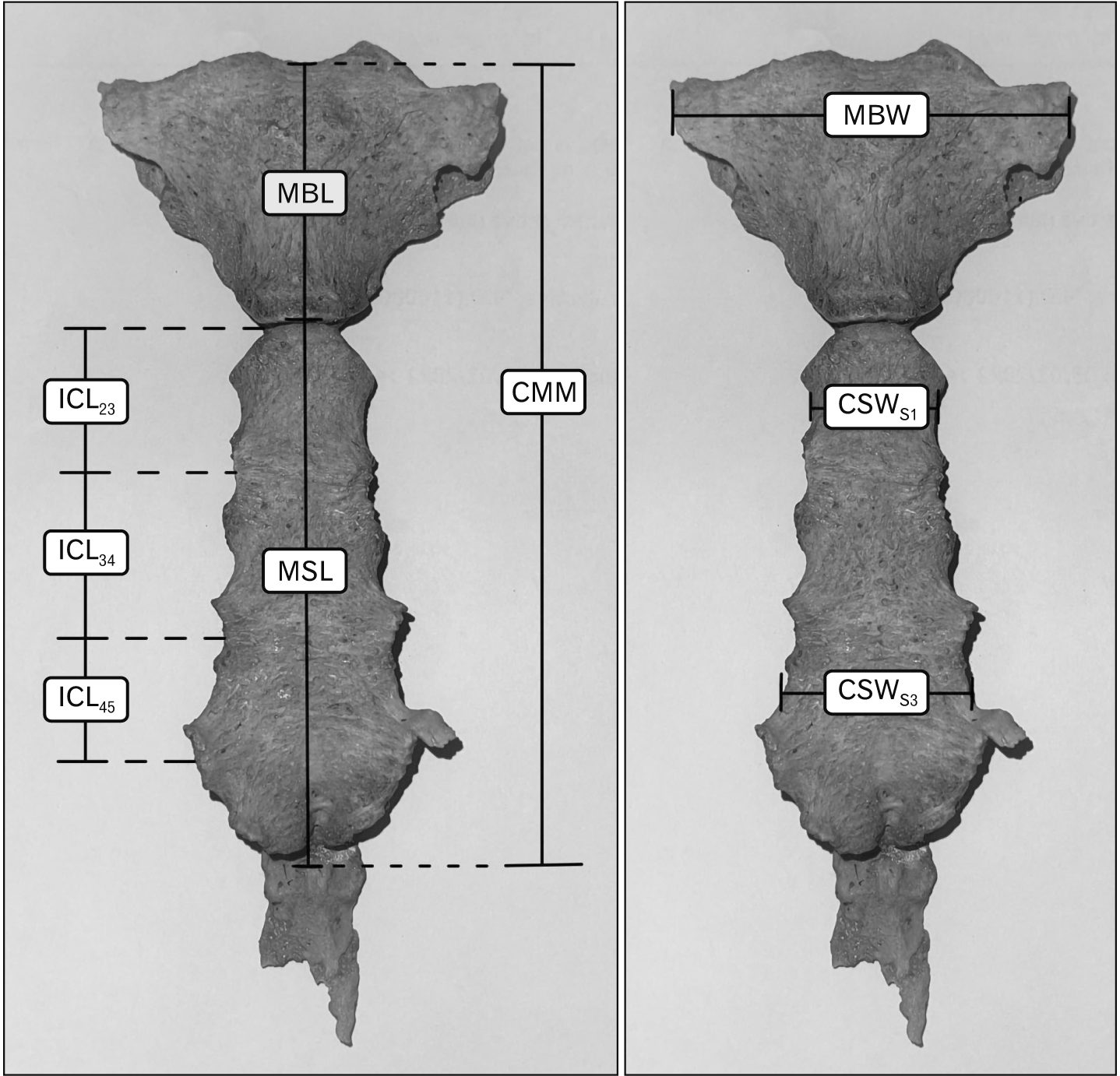
Table 1
Description of the sternal measurements
| Measurement | Abbreviation | Description |
|---|---|---|
| Manubrium length | MBL | The distance from the center of the jugular notch of the manubrium and the manubriosternal junction [12, 14]. |
| Manubrium width | MBW | The midpoint of the first costal cartilage facet on each side [14, 15]. |
| Mesosternum length | MSL | The distance from the manubriosternal junction to the mesoxiphoidal junction [12, 14]. |
| Combined length of manubrium and mesosternum | CMM | The straight distance from the center of the jugular notch of the manubrium and the mesoxiphoidal junction [12, 14]. |
| Intercostal 2nd–3rd | ICL23 | The distance from the center of costal cartilage of 2nd rib and the center cartilage of 3rd rib [12]. |
| Intercostal 3rd–4th | ICL34 | The distance from the center of costal cartilage of 3rd rib and the center cartilage of 4th rib [12]. |
| Intercostal 4th–5th | ICL45 | The distance from the center of costal cartilage of the 4th rib and the center cartilage of the 5th rib [12]. |
| Corpus sterni width at 1st sternebra | CSWS1 | The distance at the midpoint between the costal cartilage of 2nd rib and the costal cartilage 3rd rib on each side [15]. |
| Corpus sterni width at 3rd sternebra | CSWS3 | The distance at the midpoint between the costal cartilage of 4th rib and the costal cartilage 5th rib on each side [15]. |
| Sternal index | SI | Calculated by the division of Manubrium length by Mesosternum length and multiplied by 100 ([MBL/MSL]×100) [15]. |
| Sternal area | SA | Calculated by multiplying the sum of Manubrium Length and Mesosternum Length with the sum of Manubrium Width, Corpus sterni width at first sternebra, and Corpus sterni width at third sternebra divided by three ([MBL+MSL]×[MBW+CSWS1+CSWS3]/3) [15]. |
Table 2
Descriptive statistics of the measurements
Table 3
Correlation between stature and sternal measurements
Table 4
Linear regression of stature estimation model for males, females, and combined samples
MBL, manubrium length; MBW, manubrium width; MSL, mesosternum length; CMM, combined length of manubrium and mesosternum; ICL23, intercostal length between 2nd rib and 3rd rib; ICL34, intercostal length between 3rd rib and 4th rib; ICL45, intercostal length between 4th rib and 5th rib; CSWS1, corpus sterni width at first sternebra; CSWS3, corpus sterni width at third sternebra; SA, sternal area; R, correlation coefficient; R2, coefficient of determination; SEE, standard error of estimation.
Table 5
Stepwise multiple regression of stature estimation model for males, females, and combined samples
Table 6
Mean percent to the corrected stature and percent of accuracy of the test samples
Table 7
Comparing results of stature estimation using sternum with previous studies
| Study | Population | Sex | Regression | R | R2 | SEE (cm) |
|---|---|---|---|---|---|---|
| Saraf et al. [9] | Mysore Indian | Total | Simple linear | 0.891 | 0.794 | 1.620 |
| Male | Quadratic | 0.932 | 0.869 | 1.180 | ||
| Female | Quadratic | 0.904 | 0.817 | 1.530 | ||
| Macaluso and Lucena [10] | Spanish | Male | Simple linear | 0.391 | - | 6.200 |
| Female | Simple linear | 0.461 | - | 5.560 | ||
| Marinho et al. [11] | Portuguese | Male | Simple linear | 0.329 | 0.110 | 6.590 |
| Singh et al. [12] | Northwest Indian | Male | Multiple linear | - | 0.160 | 6.660 |
| Female | Simple linear | 0.318 | 0.100 | 6.650 | ||
| Tumram et al. [13] | Central Indian | Male | Simple linear | 0.550 | 0.302 | 7.400 |
| Menezes et al. [18] | South Indian | Male | Simple linear | 0.638 | - | 5.640 |
| Menezes et al. [19] | South Indian | Female | Simple linear | 0.639 | 0.408 | 4.110 |
| Yonguc et al. [20] | Turkish | Male | Simple linear | 0.721 | 0.521 | 0.045 |
| Female | Simple linear | 0.740 | 0.547 | 0.077 | ||
| Zhang et al. [21] | Western Chinese | Male | Simple linear | 0.459 | - | 4.760 |
| Female | Simple linear | 0.541 | - | 6.730 | ||
| Our study | Thai | Total | Simple linear | 0.761 | 0.573 | 6.222 |
| Male | Simple linear | 0.458 | 0.195 | 6.134 | ||
| Female | Simple linear | 0.460 | 0.204 | 5.370 |




 PDF
PDF Citation
Citation Print
Print




 XML Download
XML Download