Abstract
Determining blood loss [100% – RBV (%)] is challenging in the management of haemorrhagic shock. We derived an equation estimating RBV (%) via serial haematocrits (Hct1, Hct2) by fixing infused crystalloid fluid volume (N) as [0.015 × body weight (g)]. Then, we validated it in vivo. Mathematically, the following estimation equation was derived: RBV (%) = 24k / [(Hct1 / Hct2) – 1]. For validation, non-ongoing haemorrhagic shock was induced in Sprague–Dawley rats by withdrawing 20.0%–60.0% of their total blood volume (TBV) in 5.0% intervals (n = 9). Hct1 was checked after 10 min and normal saline N cc was infused over 10 min. Hct2 was checked five minutes later. We applied a linear equation to explain RBV (%) with 1 / [(Hct1 / Hct2) – 1]. Seven rats losing 30.0%–60.0% of their TBV suffered shock persistently. For them, RBV (%) was updated as 5.67 / [(Hct1 / Hct2) – 1] + 32.8 (95% confidence interval [CI] of the slope: 3.14–8.21, p = 0.002, R2 = 0.87). On a Bland-Altman plot, the difference between the estimated and actual RBV was 0.00 ± 4.03%; the 95% CIs of the limits of agreements were included within the pre-determined criterion of validation (< 20%). For rats suffering from persistent, non-ongoing haemorrhagic shock, we derived and validated a simple equation estimating RBV (%). This enables the calculation of blood loss via information on serial haematocrits under a fixed N. Clinical validation is required before utilisation for emergency care of haemorrhagic shock.
Haemorrhagic shock has various etiologies, including trauma, maternal haemorrhage, peptic ulcers, perioperative haemorrhage, and ruptured aortic aneurysms [1]. This medical condition causes 1.9 million deaths annually (with trauma as the leading cause; there are 1.5 million trauma-induced haemorrhagic shock deaths annually worldwide) and affects the young disproportionately raising a socioeconomic issue [2]. When trauma-related haemorrhage deteriorates, death occurs at a median of approximately 2.6 h after initial presentation addressing the importance of initial management [3,4]. Initial management is also critical for reducing delayed mortality and repaying oxygen debt before shock becomes irreversible [5]. For clinicians, prompt and correct determination of the degree of blood loss (%) is critical.
The blood loss (%) is calculated as ‘100% – residual blood volume (RBV) (%)’. For example, when RBV (%) is 65%, blood loss (%) is 35%. RBV (%) is defined as RBV/total blood volume (TBV). TBV, the denominator, is easily estimable via body weight [6]. Therefore, once RBV, the numerator, is also known, RBV (%) and thus blood loss (%) can be estimated.
The gold standard to determine RBV is a dilution method using radioactive chromium (51Cr); briefly after transfusing a small, fixed quantity of 51Cr-labelled red blood cells, the radioactivity of the blood is measured to calculate RBV [7]. The carbon monoxide rebreathing technique, which shows high reproducibility without using radioactive materials, is based on a fixed amount of an inspired oxygen-carbon monoxide gas mixture and traces the carboxyhaemoglobin (HbCO) difference to estimate RBV [8,9]. However, neither method is applicable to real-world haemorrhagic shock patients. Clinicians estimate RBV (%) or blood loss (%) considering multiple factors such as vital signs, haemoglobin/haematocrit, central venous or pulmonary capillary wedge pressure (CVP/PCWP), ultrasonography, and visual estimation [10-16]. However, these methods provide only rough estimations.
Previously, we mathematically derived an equation to estimate RBV for acute, non-ongoing haemorrhagic shock patients [17]. In mathematics class, middle school students are asked the following question: “There is a cup of sugar water with a concentration of 45%; 0.5 kg of water is poured into this mixture. The concentration of the sugar water changed to 40%. Can you calculate the initial mass of the sugar water?”. Once the initial and final concentration of sugar water and the mass of water poured into the mixture is known, it is possible to calculate the initial mass of the sugar water through a linear equation (Fig. 1A; see Supplementary Text 1A for a detailed mathematical explanation). We paid attention to the fact that this sugar water scenario is similar to that of initial management of haemorrhagic shock patients.
For patients presenting at the emergency department (ED) with haemorrhagic shock, clinicians control bleeding, request laboratory tests, infuse crystalloid fluid restrictively, and start transfusion as soon as materials are available [1,13,18]. Along with blood type, arterial blood gas analysis (ABGA), lactate, electrolytes, coagulation profiles, thromboelastography/thromboelastometry, and complete blood counts should be checked initially as point-of-care tests (POCT) [1]. With this standard management of haemorrhagic shock, the initial and final concentration of the blood, that is, the serial haematocrits (Hct1 and Hct2), become available immediately. In addition, clinicians themselves determine the volume of crystalloid fluid (N), which is infused as an initial resuscitative effort. As with the sugar water story solved by a linear equation, we derived the following equation to determine the initial blood volume (RBV) at the time of ED arrival using the information on Hct1, Hct2, and N, which are the key elements of standard management [1,13] (Fig. 1B; see Supplementary Text 1B for a detailed mathematical explanation):
The only difference between this approach and the sugar water example is k, which is approximately 0.25 for men; only a fraction of crystalloid fluid is distributed in the intravascular volume, leaving the remnant within the interstitial compartment [19].
Clinicians prefer to know blood loss (%) or RBV (%) rather than RBV itself. In this study, we mathematically derived an equation to determine the RBV (%) (and thus the blood loss [%]) by modifying the above equation and then validated it in vivo. Additionally, we also validated the original equation estimating RBV in vivo.
This study was approved by the Institutional Animal Care and Use Committee (approval number: IACUC210053) and we observed the Animal Research: Reporting of In vivo Experiments (ARRIVE) guideline in conducting this study [20].
By definition, RBV (%) is calculated as ‘RBV/TBV’. Incorporating this relationship into the original equation estimating RBV, we derive that:
Among the components, N / TBV can be substituted with a constant as follows.
In this study, we fixed N as 0.015 × body weight (g) (cc) [13,21]. We calculated TBV as 0.06 × body weight (g) + 0.77 (cc) as reported by Lee and Blaufox (r = 0.99, n = 70, p < 0.001) [22].
Incorporating this information, the equation to estimate the RBV (%) becomes far simpler:
This indicates that the RBV (%) can be determined solely by information on serial haematocrits when N is fixed.
The above equation we aimed to evaluate is a type of linear equation explaining RBV (%), the dependent variable, with 1 / [(Hct1 / Hct2) – 1] as the independent variable and 24k as the slope. To validate it, we induced varying degrees of haemorrhagic shock in a rat model. Then, we performed a linear regression analysis to obtain a regression equation in the following form: RBV (%) = 24k / [(Hct1 / Hct2) – 1] + α. As is common during updates and validations, we expected that a y-intercept, α, would be added to the original equation [23].
Using this updated equation, we estimated the RBV (%) for each rat and compared it with the ‘actual’ RBV (%). We could determine the ‘actual’ RBV (%) by pre-determining the blood loss (%), which is 100% – RBV (%), in each experiment.
We performed a correlation analysis between the actual and estimated RBVs (%) by drawing a calibration plot. Finally, drawing a Bland-Altman plot, we compared the estimated RBV (%) with the actual RBV (%) [24,25]. We expected the mean and standard deviation of their difference to be 0.0% of the TBV (0.0 cc) and 4.0% of the TBV (around 1.6 cc), respectively. In this preliminary, concept-validation study with a small sample size, we set the absolute maximum allowed difference as 20.0% of the TBV (4.0 cc). When the 95% confidence interval (CI) of the upper and lower limits of agreement were included in these maximum-allowed differences, the equation was considered validated.
We validated the original equation, RBV = k × N / [(Hct1 / Hct2) – 1], in the same way as for the RBV (%) equation. Trying to explain the RBV in terms of N / [(Hct1 / Hct2) – 1], we generated a regression equation with a slope of k and with the addition of a y-intercept. Using this updated equation, we estimated the RBV for each experiment and compared it with the actual value. After checking the degree of correlation on a calibration plot, a Bland-Altman plot was drawn to validate the equation.
Male Sprague-Dawley rats weighing 280–350 g were used in this study. They were housed in a controlled environment with free access to food and water for one week prior to the experiments.
A very strong correlation was defined as r ≥ 0.80 [26]. To accommodate an α error < 0.05, a β error < 0.20 and r ≥ 0.80, ≥ 9 rats were required. This is similar to the minimum sample size, 8, required for a Bland-Altman plot with a difference of 0.0 ± 4.0% and an absolute maximum allowed difference < 20.0%.
Considering the sample size, we simulated a 30.0% loss of TBV as well as increased blood loss in 5.0% increments (35.0%, 40.0%, and so on) within each experiment. When a rat died at a certain degree of blood loss (for example, 65.0% of TBV), we performed the same experiment again with another rat. If the next rat died, we designated the previous degree of blood loss (60.0% of TBV) as the upper limit of blood loss. We then decreased blood loss by 5.0% (25.0%, 20.0%, and so on). Similarly, when two consecutive rats failed to show signs of shock (mean arterial pressure ≤ 65 mmHg or lactate ≥ 2 mmol/L) given a certain degree of haemorrhage (e.g., 15.0% of the TBV), we designated the previous degree (e.g., 20.0% of the TBV) as the lower limit of blood loss. We expected that rats bleeding at the level of 20.0%–60.0% of TBV would be included in the current investigation, fulfilling the minimum sample size of n = 9 [11,27].
We divided the experiments into five sections, modifying a previously published model [28]. These study components were (1) preparation (baseline), (2) induction of haemorrhagic shock, (3) observation without further treatment, (4) restricted crystalloid fluid resuscitation, and (5) follow-up testing (Fig. 2). We used the subscripts 0, 1, and 2 to denote baseline before bleeding, initial ED presentation after bleeding and before fluid resuscitation, and post-fluid resuscitation status, respectively, throughout the study description.
During the study preparation phase (baseline), we injected intramuscular anesthesia into the Sprague-Dawley rats: zoletil (50 mg/kg; Virbac, Carros, France) and xylazine (10 mg/kg; Bayer, Seoul, Korea). Endotracheal intubation was performed with a 14-gauge catheter (BD Insyte, Autoguard, NJ, USA) [29]. To avoid hypoxemia and maintain normo-ventilation [13], a mechanical ventilator (Harvard rodent ventilator model 645; Harvard Apparatus, Holliston, MA, USA) was applied with a tidal volume of 2.5 ml, a respiratory rate of 50 breaths/min, and 0.21 as the fraction of inspired oxygen. A 24-gauge catheter (BD Insyte) was introduced into the left femoral artery after sterile cut-down procedure to withdraw blood, replace/infuse fluid, and monitor heart rate (HR) and systolic, diastolic, and mean arterial blood pressure (SBP, DBP, and MAP). After administering anesthesia, the procedure itself took ≤ 5 min. After the disposal of 0.2 cc within the arterial line, we performed a baseline POCT0 (ABL90 FLEX PLUS; Radiometer Medical, Copenhagen, Denmark) with the next 0.2 cc of blood to check ABGA0, lactate0, haemoglobin0, and Hct0 levels. Following this, 0.2 cc of normal saline was replaced to avoid intra-catheter clotting. Guided by ABGA0, tidal volume was adjusted to a target pH level of 7.35–7.45 and a PaCO2 level of 35–45 mmHg. Vital signs0 (SBP0, DBP0, MAP0, and HR0) were recorded throughout the procedure.
For the second phase of the study, we induced haemorrhagic shock after pre-determining the target blood loss volume as TBV × target blood loss (%). We split this target volume to lose into three. Each third was shed slowly every 2.5 min; 0.6 cc of blood had already been shed during the preparation phase (specifically, 0.2 cc of blood was used for filling the catheter hub during initial catheterisation and subsequently discarded, and 0.4 cc was used to check POCT0 levels). We compensated for this loss by subtracting 0.6 cc from the first third of blood loss volume. After each blood withdrawal, 0.1 cc of normal saline was replaced to prevent intra-catheter clotting.
Phase (3) of the study comprised observation without further treatment over the course of 10 min, simulating the prehospital situation in which a ‘scoop-and-run’ treatment approach is preferred to a ‘stay-and-play’ approach in order to prevent unnecessary delays of definitive care [1,13,30]. Haemorrhage control, which is strongly recommended within medical guidelines, was accomplished per this protocol (i.e., we did not allow further bleeding).
We recorded vital signs1 immediately before phase (4) of the study, which comprised restricting crystalloid fluid resuscitation. After discarding 0.2 cc of blood within the line, 0.2 cc of blood was sampled to check POCT1 levels (especially Hct1). We determined the volume of normal saline necessary to infuse N as 0.015 × body weight (g) (cc), which corresponds to approximately 1 L for a 70 kg adult [21,30-32]. We split N into three groups and infused fluid slowly every 5 min; The first bolus was subtracted by 0.5 cc: 0.2 cc had already been replaced after sampling for POCT0 during the preparation phase and 0.3 cc was replaced during blood loss induction.
Five minutes after completing fluid resuscitation, we initiated component (5) of the study (i.e., study follow-up). We checked POCT2 levels (including Hct2) along with vital signs2. The rats were then euthanised via cervical dislocation.
At this point, except for k, all variables for estimating the RBV became available for inclusion in the linear equations (specifically, Hct1, Hct2, and N).
Due to a calculation mistake, we withdrew 33.4% of the TBV from a rat assigned to lose 35.0% of its TBV. We analyzed this erroneous observation as though it was purposeful (i.e., we did not perform any statistical corrections and did not remove the rat from the study).
Results for body weight, V/S, and POCT were calculated as means ± standard deviations.
Linear regression analysis was performed to generate a regression equation explaining RBV in terms of k × N / [(Hct1 / Hct2) – 1] as well as with the addition of a y-intercept. Using this updated equation, we estimated the RBV for each experiment, drew a calibration plot to compare the estimated values with the actual observed values, and calculated r. Following this, a Bland-Altman plot was drawn as the final step of validation. The same procedure was used to update and validate the equations for RBV (%).
Among the nine rats that experienced haemorrhagic shock, two recovered from shock after fluid resuscitation. We performed the main analysis with seven rats showing persistent shock despite fluid resuscitation.
As a supplementary analysis, we re-conducted the analysis including all the rats regardless of persistent shock. Additionally, we performed linear regression analyses to explain RBV (%) with the following potential predictive covariates: initial and final values and interval changes for vital signs, haematocrit, and lactate.
All statistical analyses were performed using IBM SPSS statistical software, version 26 (IBM Co., Armonk, NY, USA) and MedCalc Statistical Software, version 19.2.6 (MedCalc Software Ltd., Ostend, Belgium). Statistical significance was set at a threshold of p < 0.05.
The rats suffered shock when losing ≥ 20.0% of their TBV. However, those shedding 20.0%–25.0% of their TBV recovered from shock via fluid resuscitation (Figs. 3 and 4C). Rats bleeding out 60.0% of their TBV barely survived the study protocol. A total of seven rats shedding 30.0%–60.0% of their TBV were ultimately included in the main analysis.
The rats included in the analysis weighed between 285 and 334 g and their TBV ranged from 17.87 to 20.81 cc; N spanned 4.27–5.01 cc. The mean SBP0, DBP0, and MAP0 levels were 110 ± 11, 71 ± 7, and 84 ± 8 mmHg, respectively and the mean HR0 was 215 ± 18 beats/min. Mean haemoglobin0, haematocrit0, and lactate0 levels were 13.2 ± 0.8 g/dl, 40.6 ± 2.5%, and 0.9 ± 0.3 mM, respectively. Changes in vital signs and POCT findings according to the study timeline are shown in Figs. 3 and 4, respectively.
Within a linear regression analysis among the rats shedding 30.0%–60.0% of their TBV, the equation to estimate RBV was updated as 0.272 N / [(Hct1 / Hct2) – 1] + 5.64 (95% CI of k: 0.164–0.380, p = 0.001, R2 = 0.89). In the correlation analysis between the actual and estimated RBV, r was 0.945 (p = 0.001) (Fig. 5A). On a Bland-Altman plot, the difference was 0.00 ± 0.84 cc (95% CI: –0.77, 0.78) with lower and upper limits of agreement of –1.64 (95% CI: –3.04, –0.24) cc and 1.65 (95% CI: 0.25, 3.05) cc, respectively (Fig. 5B). The pre-determined value of ± 4.0 cc included the 95% CI of these limits, thereby validating the equation.
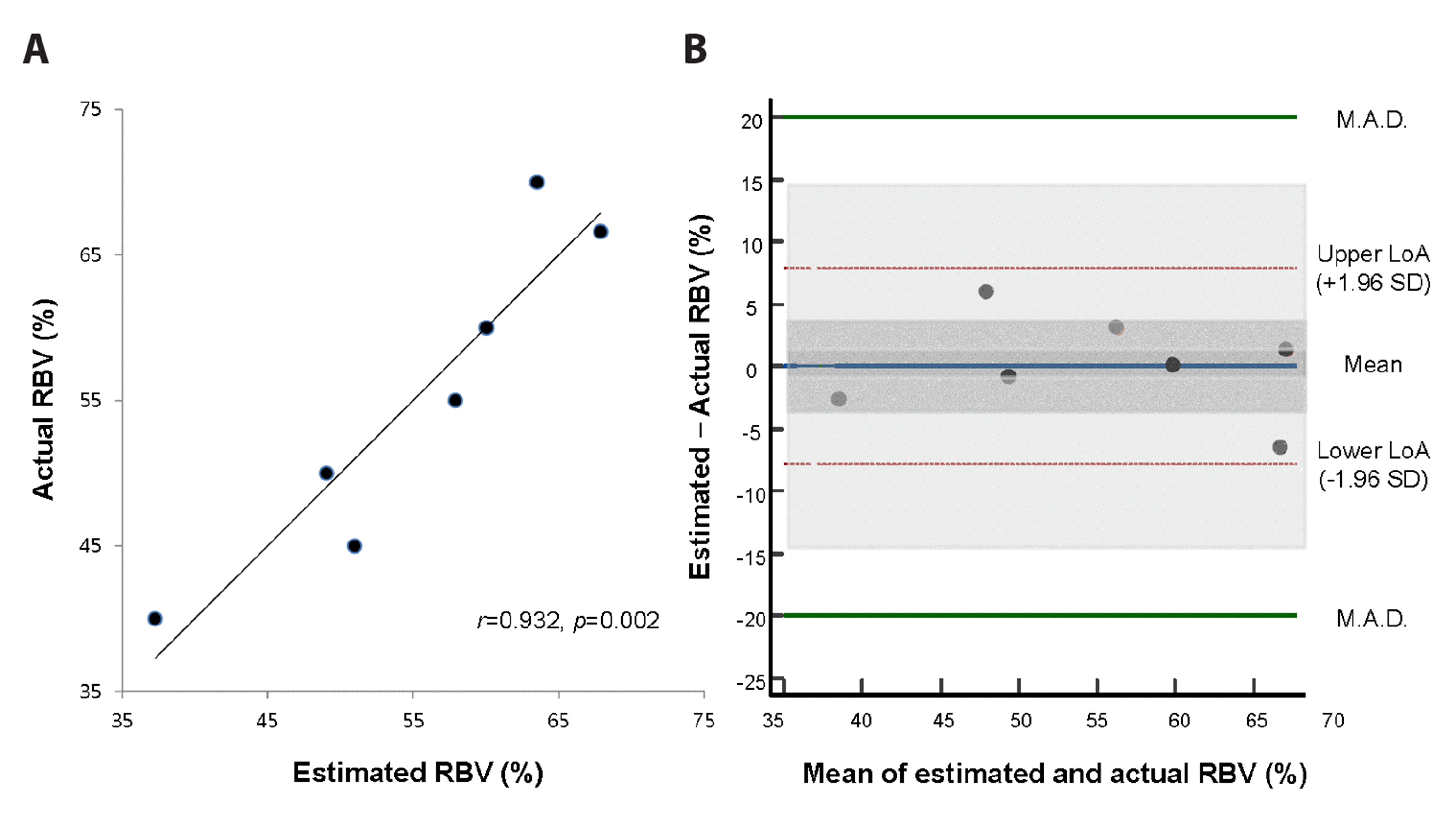
The actual RBV (%) was expressed as 5.67 / [(Hct1 / Hct2) – 1] + 32.8% (95% CI of the slope: 3.14–8.21, p = 0.002, R2 = 0.87). A calibration plot revealed that the r between the two RBV (%) was 0.932 (p = 0.002) (Fig. 6A). On a Bland-Altman plot, the difference was 0.00 ± 4.03% (95% CI: –3.71, 3.71), with lower and upper limits of agreement of –7.85% (95% CI: –14.5%, –1.18%) and 7.85% (95% CI: 1.18%, 14.5%), respectively (Fig. 6B). The 95% CIs of these limits were included within ± 20.0%, thereby validating this equation as well.
As supplementary analyses, we performed the same analyses including all nine rats that initially suffered haemorrhagic shock after bleeding. RBV was estimated as 0.302 N / [(Hct1 / Hct2) –1] + 5.72 (95% CI of the slope: 0.138–0.466, p = 0.003, R2 = 0.73). On calibration, the r between the actual and estimated RBV was 0.854 (p = 0.003) (Supplementary Fig. 1A). A Bland-Altman plot revealed a difference of 0.00 (95% CI: –1.12, 1.14) ± 1.48 cc with lower and upper limits of agreement of –2.88 (95% CI: –4.89, –0.87) cc and 2.89 (95% CI: 0.88, 4.90) cc, respectively (Supplementary Fig. 1B). Actual RBV (%) was expressed as 6.74 / [(Hct1 / Hct2) – 1] + 32.3% (95% CI of the slope: 2.29–11.2, p = 0.009, R2 = 0.65). A calibration plot revealed that the r between the actual and estimated RBV (%) was 0.804 (p = 0.009) (Supplementary Fig. 2A). On a Bland-Altman plot, the difference was 0.02 ± 8.21% (95% CI: –6.28, 6.32), with lower and upper limits of agreement of –16.0% (95% CI: –27.2%, –4.83%) and 16.1% (95% CI: 4.88%, 27.30%), respectively (Supplementary Fig. 2B). As the 95% CIs of the limits of agreement exceeded ± 4.0 cc and ± 20.0% (the pre-determined values of validation), neither equation was validated.
The results of the regression analyses examining factors associated with RBV (%) are shown in Supplementary Figs. 3–5, respectively. These figures present initial and final values and interval changes for vital signs, haematocrit, and lactate. The relevant statistics are summarised in Supplementary Table 1.
This preliminary study aimed to mathematically derive a simple equation estimating RBV (%) mathematically via serial haematocrit measurements and volumes of infused crystalloids and to validate it in vivo. For the rats that shed 30.0%–60.0% of their TBV and suffered persistent shock despite fluid resuscitation, the equation was updated and subsequently validated: RBV (%) = 6.74 / [(Hct1 / Hct2) – 1] + 32.3%. In addition, the original equation was also updated and validated: RBV = 0.272 N / [(Hct1 / Hct2) – 1] + 5.64
To our knowledge, this is the first study to suggest an equation to estimate RBV (%) mathematically in order to promptly and correctly calculate blood loss (%) [= 100% – RBV (%)] and to update and validate this equation in vivo. In addition, this is the first in vivo study to validate a mathematically derived equation estimating RBV. As all the involved variables are established components of standard haemorrhagic shock management, these equations do not require an additional apparatus or specialised testing and thus have maximal clinical applicability. If validated in human studies, these equations may help clinicians design an optimal treatment plan for patients suffering from acute, non-ongoing haemorrhagic shock at the earliest possible phase.
We conducted a regression analysis to explain RBV as a function of N / [(Hct1 / Hct2) – 1], generating a y-intercepts of 5.64. Modification of a prediction rule with the addition of a y-intercept is commonly implemented to fit a new target population during external validation [23,33]. The original equation to estimate RBV included k (the fraction of crystalloid fluid distributed in the intravascular volume) as a slope. A k of 0.272 (95% CI: 0.164, 0.380) for rats shedding 30.0%–60.0% of their TBV was observed for this experimental group. This seems to match the k values reported for humans, which is reported to be approximately 0.25 [19].
Supplementary analyses revealed that the regression equations implemented for rats suffering from persistent shock despite fluid resuscitation were superior to those implemented among all the rats regardless of persistent shock shedding (i.e., 20.0%–60.0% TBV). In estimating RBV (%), the former showed greater a R2 (0.87 vs. 0.65) and a narrower 95% CI of the slope (5.67 [3.14–8.21] vs. 6.74 [2.29–11.2]). By excluding the two rats shedding 20.0%–25.0% of their TBV, the equation provided a superior explanation of RBV (%) via the equation 24k / [(Hct1 / Hct2) – 1] and specified the slope more precisely. Though we are unsure why the rats that lost 20.0%–25.0% of their TBV distorted the equations, the following observations as well as knowledge of the relevant literature provide important context for interpreting these findings. Just before crystalloid fluid resuscitation, their MAP1 levels were 63 and 65 mmHg, respectively (Fig. 3C). After fluid resuscitation, their MAP2 levels increased to 117 and 84 mmHg, respectively, exceeding 65 mmHg (the criterion of shock). Their lactate levels were persistently < 2.0 mM, failing to fulfill another criterion of shock (Fig. 4C). The more MAP out-ranges above shock level, the more urine is excreted [34,35]. This leakage of the circulatory system via the urinary system violates the basic assumptions of the current equations and may have isolated these two rats as outliers [17].
Clinicians have estimated RBV (%) or blood loss (%) using vital signs, haemoglobin/haematocrit measurements, CVP/PCWP, ultrasonography, and visual estimation. Although useful, these methods provide only rough estimations. Tachycardia and hypotension, occurring within class I, II (mild), III (moderate), and IV (severe) haemorrhagic shock, are less reliable indicators for patients receiving antihypertensive medications (especially beta or calcium channel blocking medications) and their sensitivities are unsatisfactory [11,16]. Haematocrit does not reflect acute haemorrhage adequately as the plasma volume fails to increase sufficiently for achieving an euvolemic state [36]. Neither CVP nor PCWP predicts ventricular preload (which correlates with RBV) [37]. Although ultrasonography provides some hints regarding preload with respect to the diameter and collapsibility of the inferior vena cava as well as fluid responsiveness, these indicate RBV (%) indirectly; fluid challenge is less applicable for haemorrhagic shock patients whose fluid resuscitation should be restricted [18,38]. Meanwhile, visual estimation of blood loss is inaccurate and unreliable even in the operating room [14]. Due to these limitations, researchers combined these variables to enhance diagnostic accuracy [10,12]. For example, Callcut and colleagues suggested that massive transfusion is indicated when two of following factors are present: an international normalised ratio (INR) > 1.5, SBP < 90 mmHg, haemoglobin < 11 g/dl, a base deficit of ≥ 6 mM, and fluid revealed on focused assessment with sonography for trauma (sensitivity 85%, specificity 41%) [10]. However, these rules are relatively non-specific and cannot differentiate RBV (%) quantitatively.
Some researchers previously investigated the volume of infused crystalloid fluid or serial haematocrits (the key variables of the current study) as tools for RBV (%) estimation. The response to initial fluid resuscitation is suggested to help estimate blood loss (%), with rapid, transient, and minimal/no response correspond to minimal (< 15%), moderate and ongoing (15%–40%), and severe (> 40%) loss of TBV, respectively [11]. However, this approach cannot estimate RBV (%) quantitatively in order to guide fluid/blood resuscitation delicately, as required for successful haemorrhagic shock management.
Thorson and colleagues reported that Hct1–Hct2 > 6% reliably indicate ongoing bleeding [39]. However, only 3.9% (9/232) of their study participants suffered shock and the interval to check the serial haematocrits was 120 ± 63 min even for patients with ongoing bleeding. These rendered their results less applicable for haemorrhagic shock, which required much faster fluid resuscitation followed by a repeat haematocrit measurement; 60% of patients die within 3 h after ED presentation for haemorrhagic shock [4]. Meanwhile, the current study (that dealt with the earliest phase of haemorrhagic shock) showed some correlation between Hct1–Hct2 and RBV (%) (Supplementary Fig. 5F, Supplementary Table 1). This association may be explained mathematically using our equation:
As mentioned above, the equation to estimate RBV (%) contains Hct1–Hct2 as a denominator. However, considering the effect of the numerator (Hct2) on the whole equation, the equation including both the numerator and denominator is more robust than Hct1–Hct2 alone. The R2 of our regression equation (0.87) is greater than that including Hct1–Hct2 alone (0.59), supporting its superiority in terms of explaining RBV (%).
By replacing N/TBV with 0.24 in rats, we simplified the equation to estimate RBV (%) from k × N / TBV / [(Hct1 / Hct2) – 1] × 100 (%) to 24k / [(Hct1 / Hct2) – 1] (%). The only condition was pre-determination of N in terms of body weight (0.015 cc/g in this study). This suggests that RBV (%), and thus blood loss (%) (100%–RBV [%]) can be determined by Hct1 and Hct2 when a fixed N is infused. For a human, TBV (L/kg) is approximately 0.075 × (body weight) for men and 0.065 × (body weight) for women [6]. When N is fixed as 0.015 L/kg, which corresponds to 1 L for 70 kg adults (in line with standard management of haemorrhagic shock), N/TBV is 0.20 for men and 0.23 for women. If k is 0.25, as reported previously [19], the following equations may be applicable for non-ongoing haemorrhagic shock patients:
Of course, further clinical studies are required to modify these equations, including adjustment of the slope and the addition of a y-intercept [23].
In supplementary analyses, RBV (%) was closely associated with both initial and final values of SBP, DBP, MAP, lactate, and haematocrit (R2: 0.50–0.91, with all p < 0.05; Supplementary Table 1 and Supplementary Figs. 1, 2). However, we regarded these results as inapplicable in practice. For instance, we strictly controlled the time of bleeding, observation, and fluid resuscitation in this animal study. However, haemorrhagic shock patients arrive at the ED at various times following the time of initial bleeding. Because blood pressure, lactate, and haematocrit changes over time even in the same patient [28], these variables measured at strict timelines in a laboratory setting are not applicable to real haemorrhagic shock patients.
This study had several limitations. First, this study dealt with ‘non-ongoing’ haemorrhagic shock. This confines the indication of this work to patients for whom instant haemostasis is achievable (for example, patients with penetrating extremity wounds, peptic ulcers, or perioperative bleeding). For most blunt trauma, maternal haemorrhage, and ruptured aortic aneurysm cases (i.e., the other major causes of mortality due to haemorrhagic shock), instant haemostasis may be difficult to achieve, thus rendering our study results less applicable [1,3]. However, the current equations may have some value even for ongoing haemorrhagic shock patients; for example, Hct2 would be lower among ongoing haemorrhagic shock patients than among non-ongoing haemorrhagic shock patients (e.g., 30.0% vs. 32.0%). Incorporating this lowered Hct2 into the equation as 6.74 / [(Hct1 / Hct2) – 1] + 32.3 (%), while assuming Hct1 = 40.0% in this example, would cause RBV (%) to be underestimated (52.5% vs. 59.3%). Therefore, for patients with ongoing haemorrhagic shock, the actual initial RBV (%) must be larger than the value estimated by the equation (52.5% in this example). Clinicians may not know whether bleeding is ongoing. Even in this situation, they may guess that the initial RBV (%) would be at least equal to the estimated value (52.5% in case of a non-ongoing haemorrhage) or larger (in case of an ongoing haemorrhage). Second, bleeding was induced simply by puncturing the left femoral artery. With this low energy injury, we could assume that k would not vary significantly. However, in severe trauma, broken endothelial glycocalyx layers and coagulopathy caused by oxygen debt lead to increased vascular permeability and extravasation of intravascular fluid into the interstitial space (especially under lower oncotic pressure), thus lowering k [40-42]. In this situation, k might fluctuate according to the type and severity of the injury, thus making the equations less applicable in their current forms. Third, in this preliminary, concept-validating study, we set the absolute maximum allowed difference between the estimated and actual residual blood as < 20.0%, assuming a mean difference of 0.0 ± 4.0%. For rats shedding 30.0%–60.0% of their TBV, the actual maximum difference in this study was –6.5%, far smaller than the pre-determined value of ± 20%. However, considering the small sample size in this current study, we had to compensate for the wide 95% CIs of the upper and lower limits of agreement. The issue of sample size needs to be considered carefully within further clinical studies conducted to validate the concept of this study.
Considering these limitations, we believe that this preliminary concept-validation study is a starting point for further investigations. First, the equation to estimate the RBV (%) needs to be established clinically in non-ongoing, haemorrhagic shock patients and in studies with a larger sample size. Although we proposed 5.0 / [(Hct1 / Hct2) – 1] (%) for men and 5.8 / [(Hct1 / Hct2) – 1] (%) for women (assuming a k of 0.25), these equations would need clinical validation, including adjustment of the k value and assignment of a y-intercept [23]. Second, preclinical or clinical studies aiming to broaden the indications of the current equations are required, including those for ongoing haemorrhage and high-energy blunt injury. In contrast to animal studies wherein researchers can freely pre-determine the degree of bleeding, it may be difficult to determine the ‘actual’ RBV (or blood loss), which is the reference value to compare the ‘estimated’ RBV with, among the actual haemorrhagic shock patients. We propose that, among the patients undergoing major surgery that tends to cause profuse bleeding, our concept can be validated while the anaesthesiologists monitor input/output of fluid, vital signs, and POCT on a real time basis. More practically, the ability to predict the need for massive transfusion among haemorrhagic shock patienta may be compared using the equation we suggest in this study and the current indexes composed of several variables at ED [10,12]. Meanwhile, whether our equation is associated with the clinical indexes such as SOFA (sequential organ failure assessment) and SAPS (simplified acute physiologic score) II may be also investigated. These indexes are expected to be worse in patients with more blood loss because of the hypoperfusion secondary to multiple organ injuries [43-45]. Furthermore, if our equation shows a direct relationship with the occurrence of multiple organ failure and mortality, it can potentially be easily adopted by clinicians considering its immediate availability and simplicity.
In summary, this concept-derivation and preliminary in vivo validation study demonstrates that RBV (%) and thus blood loss (%) may be calculable via information on serial haematocrits and the volume of crystalloid fluid infused for rats suffering from acute, non-going haemorrhagic shock. The equations we suggest in the study seem to apply best for rats suffering from persistent haemorrhagic shock despite crystalloid fluid resuscitation. Further studies are required to validate the clinical applicability of these equations and to widen their indications, regardless of ongoing haemorrhage, injury mechanism, and severity.
Supplementary data including one text, five figures, and one table can be found with this article online at https://doi.org/10.4196/kjpp.2022.26.3.195.
ACKNOWLEDGEMENTS
The authors express their cordial gratitude to Prof. Sang Do Shin for his insightful mentoring in this study. We also appreciate Miss Ha Eun Lee, BS, and Ye-Hee Chon for their help in performing the experiment and drafting figures, respectively. We thank Editage.com for English language editing.
REFERENCES
1. Cannon JW. 2018; Hemorrhagic Shock. N Engl J Med. 378:370–379. DOI: 10.1056/NEJMra1705649. PMID: 29365303.

2. Lozano R, Naghavi M, Foreman K, Lim S, Shibuya K, Aboyans V, Abraham J, Adair T, Aggarwal R, Ahn SY, Alvarado M, Anderson HR, Anderson LM, Andrews KG, Atkinson C, Baddour LM, Barker-Collo S, Bartels DH, Bell ML, Benjamin EJ, et al. 2012; Global and regional mortality from 235 causes of death for 20 age groups in 1990 and 2010: a systematic analysis for the Global Burden of Disease Study 2010. Lancet. 380:2095–2128. Erratum in: Lancet. 2013;381:628. DOI: 10.1016/S0140-6736(12)61728-0. PMID: 23245604.
3. Tien HC, Spencer F, Tremblay LN, Rizoli SB, Brenneman FD. 2007; Preventable deaths from hemorrhage at a level I Canadian trauma center. J Trauma. 62:142–146. DOI: 10.1097/01.ta.0000251558.38388.47. PMID: 17215745.

4. Holcomb JB, del Junco DJ, Fox EE, Wade CE, Cohen MJ, Schreiber MA, Alarcon LH, Bai Y, Brasel KJ, Bulger EM, Cotton BA, Matijevic N, Muskat P, Myers JG, Phelan HA, White CE, Zhang J, Rahbar MH. 2013; The prospective, observational, multicenter, major trauma transfusion (PROMMTT) study: comparative effectiveness of a time-varying treatment with competing risks. JAMA Surg. 148:127–136. DOI: 10.1001/2013.jamasurg.387. PMID: 23560283. PMCID: PMC3740072.

5. Barbee RW, Reynolds PS, Ward KR. 2010; Assessing shock resuscitation strategies by oxygen debt repayment. Shock. 33:113–122. DOI: 10.1097/SHK.0b013e3181b8569d. PMID: 20081495.

6. Butterworth JF, Mackey DC, Wasnick JD. 2018. Morgan and Mikhail's clinical anesthesiology. 6th ed. McGraw-Hill Education LLC.;New York: DOI: 10.1097/shk.0b013e3181b8569d.
7. 1980; Recommended methods for measurement of red-cell and plasma volume: International Committee for Standardization in Haematology. J Nucl Med. 21:793–800. PMID: 7400838.
8. Falz R, Busse M. 2018; Determination of hemoglobin mass in humans by measurement of CO uptake during inhalation of a CO-air mixture: a proof of concept study. Physiol Rep. 6:e13849. DOI: 10.14814/phy2.13849. PMID: 30178548. PMCID: PMC6121115.

9. Plumb JOM, Kumar S, Otto J, Schmidt W, Richards T, Montgomery HE, Grocott MPW. 2018; Replicating measurements of total hemoglobin mass (tHb-mass) within a single day: precision of measurement; feasibility and safety of using oxygen to expedite carbon monoxide clearance. Physiol Rep. 6:e13829. DOI: 10.14814/phy2.13829. PMID: 30203465. PMCID: PMC6131726.

10. Callcut RA, Cotton BA, Muskat P, Fox EE, Wade CE, Holcomb JB, Schreiber MA, Rahbar MH, Cohen MJ, Knudson MM, Brasel KJ, Bulger EM, Del Junco DJ, Myers JG, Alarcon LH, Robinson BR. 2013; Defining when to initiate massive transfusion: a validation study of individual massive transfusion triggers in PROMMTT patients. J Trauma Acute Care Surg. 74:59–65. 67–68. discussion 66–67. DOI: 10.1097/TA.0b013e3182788b34. PMID: 23271078. PMCID: PMC3771339.
11. American College of Surgeons, Committee on Trauma. 2018. Advanced trauma life support: student course manual. 8th ed. American College of Surgeons;Chicago:
12. Cotton BA, Dossett LA, Haut ER, Shafi S, Nunez TC, Au BK, Zaydfudim V, Johnston M, Arbogast P, Young PP. 2010; Multicenter validation of a simplified score to predict massive transfusion in trauma. J Trauma. 69 Suppl 1:S33–S39. DOI: 10.1097/TA.0b013e3181e42411. PMID: 20622617.

13. Rossaint R, Bouillon B, Cerny V, Coats TJ, Duranteau J, Fernández-Mondéjar E, Filipescu D, Hunt BJ, Komadina R, Nardi G, Neugebauer EA, Ozier Y, Riddez L, Schultz A, Vincent JL, Spahn DR. 2016; The European guideline on management of major bleeding and coagulopathy following trauma: fourth edition. Crit Care. 20:100. DOI: 10.1186/s13054-016-1265-x. PMID: 27072503. PMCID: PMC4828865.

14. Rothermel LD, Lipman JM. 2016; Estimation of blood loss is inaccurate and unreliable. Surgery. 160:946–953. DOI: 10.1016/j.surg.2016.06.006. PMID: 27544540.

15. Dipti A, Soucy Z, Surana A, Chandra S. 2012; Role of inferior vena cava diameter in assessment of volume status: a meta-analysis. Am J Emerg Med. 30:1414–1419.e1. DOI: 10.1016/j.ajem.2011.10.017. PMID: 22221934.

16. Newgard CD, Cheney TP, Chou R, Fu R, Daya MR, O'Neil ME, Wasson N, Hart EL, Totten AM. 2020; Out-of-hospital circulatory measures to identify patients with serious injury: a systematic review. Acad Emerg Med. 27:1323–1339. DOI: 10.1111/acem.14056. PMID: 32558073.

17. Oh WS, Chon SB. 2016; Calculation of the residual blood volume after acute, non-ongoing hemorrhage using serial hematocrit measurements and the volume of isotonic fluid infused: theoretical hypothesis generating study. J Korean Med Sci. 31:814–816. DOI: 10.3346/jkms.2016.31.5.814. PMID: 27134507. PMCID: PMC4835611.

18. Chang R, Holcomb JB. 2017; Optimal fluid therapy for traumatic hemorrhagic shock. Crit Care Clin. 33:15–36. DOI: 10.1016/j.ccc.2016.08.007. PMID: 27894494. PMCID: PMC5131713.

19. Imm A, Carlson RW. 1993; Fluid resuscitation in circulatory shock. Crit Care Clin. 9:313–333. DOI: 10.1016/S0749-0704(18)30198-2. PMID: 8490765.

20. Percie du Sert N, Ahluwalia A, Alam S, Avey MT, Baker M, Browne WJ, Clark A, Cuthill IC, Dirnagl U, Emerson M, Garner P, Holgate ST, Howells DW, Hurst V, Karp NA, Lazic SE, Lidster K, MacCallum CJ, Macleod M, Pearl EJ, et al. 2020; Reporting animal research: explanation and elaboration for the ARRIVE guidelines 2.0. PLoS Biol. 18:e3000411. DOI: 10.1371/journal.pbio.3000411. PMID: 32663221. PMCID: PMC7360025. PMID: 0cdc6121568245e7b56bd1cca7b31653.

21. Ley EJ, Clond MA, Srour MK, Barnajian M, Mirocha J, Margulies DR, Salim A. 2011; Emergency department crystalloid resuscitation of 1.5 L or more is associated with increased mortality in elderly and nonelderly trauma patients. J Trauma. 70:398–400. DOI: 10.1097/TA.0b013e318208f99b. PMID: 21307740.

22. Lee HB, Blaufox MD. 1985; Blood volume in the rat. J Nucl Med. 26:72–76. PMID: 3965655.
23. Moons KG, Kengne AP, Grobbee DE, Royston P, Vergouwe Y, Altman DG, Woodward M. 2012; Risk prediction models: II. External validation, model updating, and impact assessment. Heart. 98:691–698. DOI: 10.1136/heartjnl-2011-301247. PMID: 22397946.

24. Bland JM, Altman DG. 1986; Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1:307–310. DOI: 10.1016/S0140-6736(86)90837-8. PMID: 2868172.

25. Giavarina D. 2015; Understanding Bland Altman analysis. Biochem Med (Zagreb). 25:141–151. DOI: 10.11613/BM.2015.015. PMID: 26110027. PMCID: PMC4470095.

26. Chan YH. 2003; Biostatistics 104: correlational analysis. Singapore Med J. 44:614–619. PMID: 14770254.
27. Fülöp A, Turóczi Z, Garbaisz D, Harsányi L, Szijártó A. 2013; Experimental models of hemorrhagic shock: a review. Eur Surg Res. 50:57–70. DOI: 10.1159/000348808. PMID: 23615606.

28. Lee JH, Kim K, Jo YH, Kim MA, Lee KB, Rhee JE, Doo AR, Lee MJ, Park CJ, Kim J, Chung H. 2014; Blood pressure-targeted stepwise resuscitation for hemorrhagic shock in rats. J Trauma Acute Care Surg. 76:771–778. DOI: 10.1097/TA.0000000000000106. PMID: 24553547.

29. Mayglothling J, Duane TM, Gibbs M, McCunn M, Legome E, Eastman AL, Whelan J, Shah KH. 2012; Emergency tracheal intubation immediately following traumatic injury: an Eastern Association for the Surgery of Trauma practice management guideline. J Trauma Acute Care Surg. 73(5 Suppl 4):S333–S340. DOI: 10.1097/TA.0b013e31827018a5. PMID: 23114490.
30. Cotton BA, Jerome R, Collier BR, Khetarpal S, Holevar M, Tucker B, Kurek S, Mowery NT, Shah K, Bromberg W, Gunter OL, Riordan WP Jr. 2009; Guidelines for prehospital fluid resuscitation in the injured patient. J Trauma. 67:389–402. DOI: 10.1097/TA.0b013e3181a8b26f. PMID: 19667896.

31. Kwan I, Bunn F, Roberts I. 2003; Timing and volume of fluid administration for patients with bleeding. Cochrane Database Syst Rev. (3):CD002245. DOI: 10.1002/14651858.CD002245. PMID: 24599652. PMCID: PMC7133544.

32. Shafi S, Collinsworth AW, Richter KM, Alam HB, Becker LB, Bullock MR, Ecklund JM, Gallagher J, Gandhi R, Haut ER, Hickman ZL, Hotz H, McCarthy J, Valadka AB, Weigelt J, Holcomb JB. 2016; Bundles of care for resuscitation from hemorrhagic shock and severe brain injury in trauma patients-Translating knowledge into practice. J Trauma Acute Care Surg. 81:780–794. DOI: 10.1097/TA.0000000000001161. PMID: 27389129.

33. Toll DB, Janssen KJ, Vergouwe Y, Moons KG. 2008; Validation, updating and impact of clinical prediction rules: a review. J Clin Epidemiol. 61:1085–1094. DOI: 10.1016/j.jclinepi.2008.04.008. PMID: 19208371.

34. Hahn RG. 2017; Arterial pressure and the rate of elimination of crystalloid fluid. Anesth Analg. 124:1824–1833. DOI: 10.1213/ANE.0000000000002075. PMID: 28452823.

35. Hultström M. 2013; Neurohormonal interactions on the renal oxygen delivery and consumption in haemorrhagic shock-induced acute kidney injury. Acta Physiol (Oxf). 209:11–25. DOI: 10.1111/apha.12147. PMID: 23837642.

36. Valeri CR, Dennis RC, Ragno G, Macgregor H, Menzoian JO, Khuri SF. 2006; Limitations of the hematocrit level to assess the need for red blood cell transfusion in hypovolemic anemic patients. Transfusion. 46:365–371. DOI: 10.1111/j.1537-2995.2006.00730.x. PMID: 16533277.

37. Kumar A, Anel R, Bunnell E, Habet K, Zanotti S, Marshall S, Neumann A, Ali A, Cheang M, Kavinsky C, Parrillo JE. 2004; Pulmonary artery occlusion pressure and central venous pressure fail to predict ventricular filling volume, cardiac performance, or the response to volume infusion in normal subjects. Crit Care Med. 32:691–699. DOI: 10.1097/01.CCM.0000114996.68110.C9. PMID: 15090949.

38. McLean AS. 2016; Echocardiography in shock management. Crit Care. 20:275. DOI: 10.1186/s13054-016-1401-7. PMID: 27543137. PMCID: PMC4992302.

39. Thorson CM, Ryan ML, Van Haren RM, Pereira R, Olloqui J, Otero CA, Schulman CI, Livingstone AS, Proctor KG. 2013; Change in hematocrit during trauma assessment predicts bleeding even with ongoing fluid resuscitation. Am Surg. 79:398–406. DOI: 10.1177/000313481307900430. PMID: 23574851.

40. Kleinveld DJB, Botros L, Maas MAW, Kers J, Aman J, Hollmann MW, Juffermans NP. 2021; Bosutinib reduces endothelial permeability and organ failure in a rat polytrauma transfusion model. Br J Anaesth. 126:958–966. DOI: 10.1016/j.bja.2021.01.032. PMID: 33685634. PMCID: PMC8258973.

41. Rahbar E, Cardenas JC, Baimukanova G, Usadi B, Bruhn R, Pati S, Ostrowski SR, Johansson PI, Holcomb JB, Wade CE. 2015; Endothelial glycocalyx shedding and vascular permeability in severely injured trauma patients. J Transl Med. 13:117. DOI: 10.1186/s12967-015-0481-5. PMID: 25889764. PMCID: PMC4397670.

42. White NJ, Ward KR, Pati S, Strandenes G, Cap AP. 2017; Hemorrhagic blood failure: oxygen debt, coagulopathy, and endothelial damage. J Trauma Acute Care Surg. 82(6S Suppl 1):S41–S49. DOI: 10.1097/TA.0000000000001436. PMID: 28328671. PMCID: PMC5488798.
43. Hamon A, Mokart D, Pouliquen C, Guibert JM, Cambon S, Duong LN, Lambaudie E, Sannini A, Chow-Chine L, Bisbal M, Ewald J, Turrini O, Faucher M. 2020; Intraoperative hemorrhagic shock in cancer surgical patients: short and long-term mortality and associated factors. Shock. 54:659–666. DOI: 10.1097/SHK.0000000000001537. PMID: 32205792.

44. Ferreira FL, Bota DP, Bross A, Mélot C, Vincent JL. 2001; Serial evaluation of the SOFA score to predict outcome in critically ill patients. JAMA. 286:1754–1758. DOI: 10.1001/jama.286.14.1754. PMID: 11594901.

45. Minne L, Abu-Hanna A, de Jonge E. 2008; Evaluation of SOFA-based models for predicting mortality in the ICU: a systematic review. Crit Care. 12:R161. DOI: 10.1186/cc7160. PMID: 19091120. PMCID: PMC2646326.

Fig. 1
Analogy between the change of concentration of sugar water after adding some water and that of haematocrit of blood after crystalloid fluid infusion.
(A) Change of concentration of sugar water after adding some water. Once you know the initial and final concentration of sugar water and the mass of water poured into it, you can tell the initial mass of the sugar water by building a linear equation (see Supplementary Text 1A for detailed explanation). (B) Change of haematocrit of blood after crystalloid fluid infusion. Likewise, if there is no blood or fluid loss via the circulation system, residual blood volume (RBV) would be calculable with serial haematocrits (Hct1 and Hct2) and the volume of crystalloid fluid infused in-between (N). The only difference from (A) is that only a certain fraction (k, which is approximately 0.25 for men) would be distributed into the intravascular volume (See Supplementary Text 1B for detailed explanation).
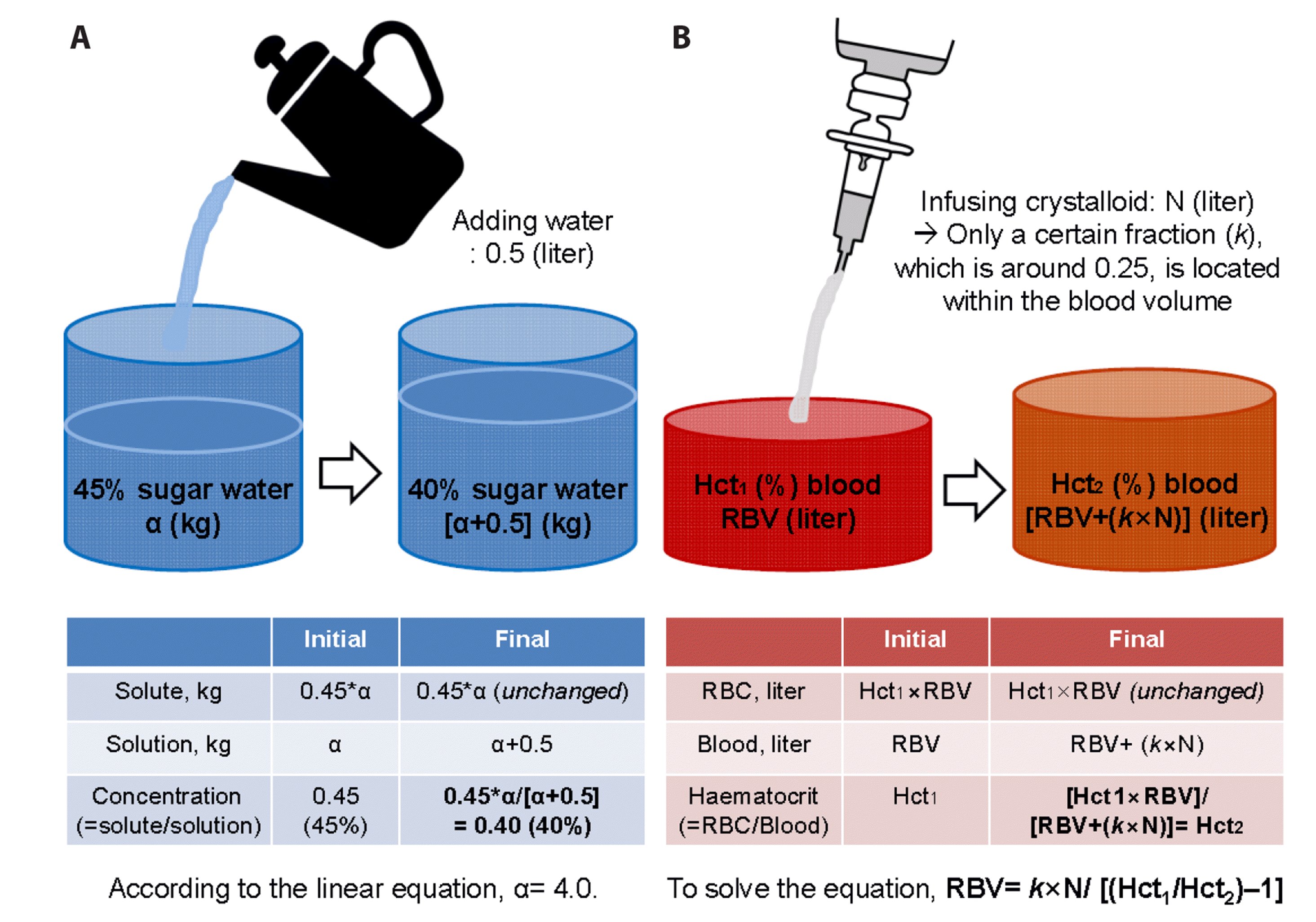
Fig. 2
Study protocol.
POCT, point-of-care test including arterial blood gas analysis, haematocrit, and lactate; V/S, vital signs including systolic, diastolic, and mean arterial blood pressure and heart rate. Subscripts 0, 1, and 2 denote baseline before bleeding, status just before fluid resuscitation, and status after fluid resuscitation, respectively.
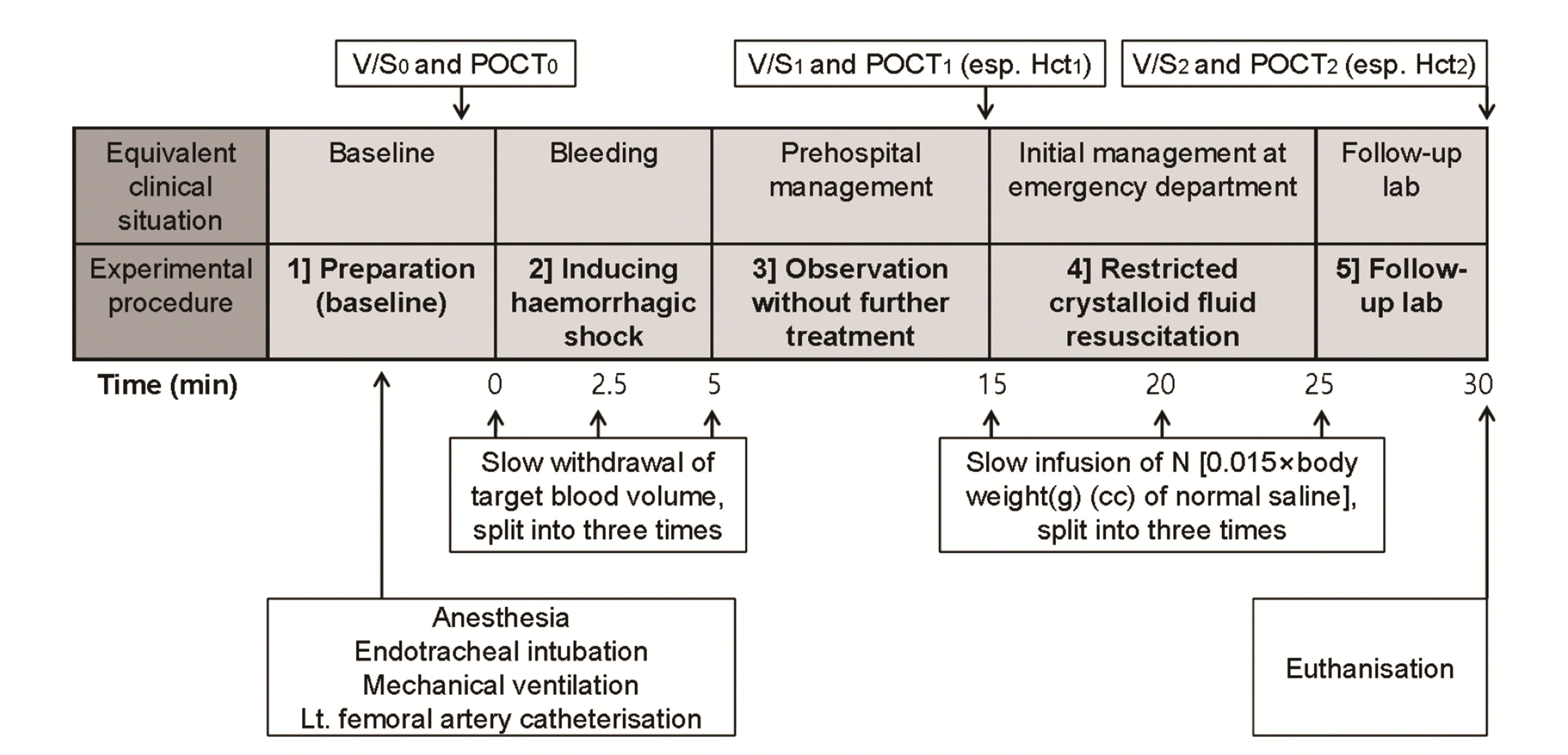
Fig. 3
Vital signs at the time of baseline (time 0), before (time 1), and after (time 2) crystalloid fluid resuscitation.
(A) Systolic blood pressure. (B) Diastolic blood pressure. (C) Mean arterial pressure. (D) Heart rate.
Fig. 4
Laboratory findings at the time of baseline (time 0), before (time 1), and after (time 2) crystalloid fluid resuscitation.
(A) pH. (B) Partial oxygen pressure (PO2). (C) Lactate. (D) Haematocrit.
Fig. 5
Relation between actual and estimated residual blood volume (RBV) among the seven rats that showed persistent shock despite fluid resuscitation.
(A) Relation between actual RBV and estimated RBV calculated as 0.272N / [(Hct1 / Hct2) – 1] + 5.64. (B) Bland-Altman plot with shades showing 95% CI of mean, upper and lower limits of agreement. Hct1, initial haematocrit; Hct2, subsequent haematocrit; LoA, limit of agreement; M.A.D., maximum allowed difference (pre-determined); N, volume of crystalloid fluid infused in-between; SD, standard deviation; CI, confidence interval.
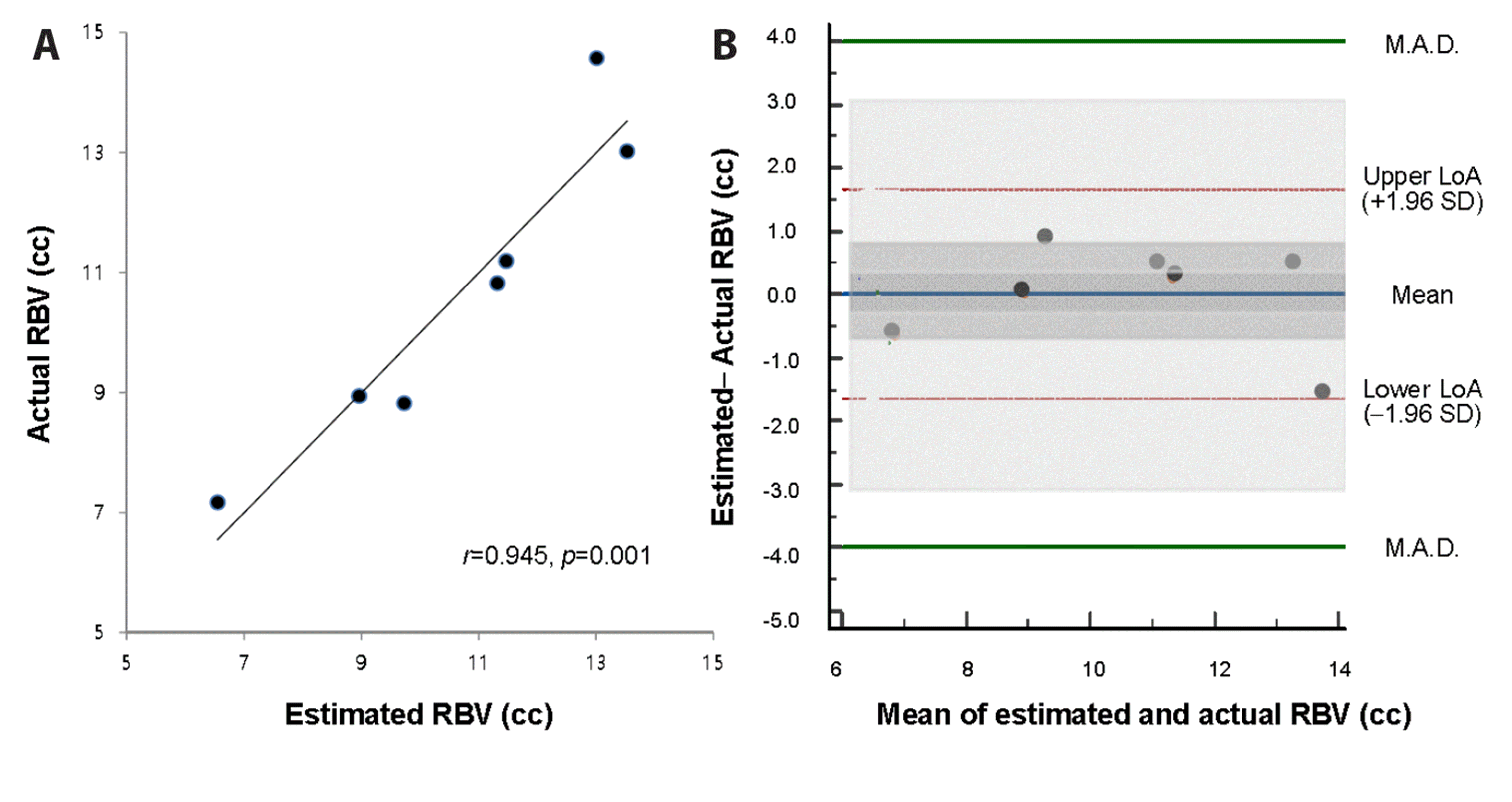
Fig. 6
Relation between actual and estimated residual blood volume (RBV) (%) among the seven rats that showed persistent shock despite fluid resuscitation.
(A) Relation between actual RBV (%) and estimated RBV (%) calculated as 6.74 / [(Hct1 / Hct2) – 1] + 32.3. (B) Bland-Altman plot with shades showing 95% CI of mean, upper and lower limits of agreement. Hct1, initial haematocrit; Hct2, subsequent haematocrit; LoA, limit of agreement; M.A.D., maximum allowed difference (pre-determined); RBV, residual blood volume; SD, standard deviation; CI, confidence interval.




 PDF
PDF Citation
Citation Print
Print


 XML Download
XML Download