This article has been
cited by other articles in ScienceCentral.
Abstract
Purpose
To evaluate the effects of load direction, number of implants, and alignment of implant position on stress distribution in implant, prosthesis, and bone tissue.
Materials and Methods
Four 3D models were made to simulate posterior mandible bone block: two implants and 3-unit fixed dental prosthesis (FDP) with a pontic in the center (model M1), two implants and 3-unit FDP with a cantilever pontic at one end (model M2), FDP supported by three implants with straight line placement (model M3) and FDP supported by three implants with staggered implant configuration (model M4). The applied force was 120 N axially or 120 N obliquely.
Results
Peak von Mises stresses caused by oblique occlusal force were 3.4 to 5.1 times higher in the implant and 3.5 to 8.3 times higher in the alveolar bone than those stresses caused by axial occlusal force. In model M2, the connector area of the distal cantilever in the prosthesis generated the highest von Mises stresses among all models. With the design of a large number of implants, low stresses were generated. When three implants were placed, there were no significant differences in the magnitude of stress between staggered arrangement and straight arrangement.
Conclusion
The effect of staggering alignment on implant stress was negligible. However, the number of implants had a significant effect on stress magnitude.
Go to :

초록
목적
수복물에 교합력을 가할때 식립된 임플란트의 개수, 배열 및 위치에 따른 임플란트, 보철물 및 지지 골에 발생하는 응력의 차이를 분석하고자 한다.
연구 재료 및 방법
하악에 임플란트가 식립되어 고정성 보철물을 지지하는 4 종류의 3D 유한요소 모형을 제작하였다. 모델 M1은 2개의 임플란트 가운데에 가공치를 배열하였고, 모델 M2는 2개의 임플란트 외측에 캔티레버 가공치를 배열하였다. 모델 M3과 M4는 3개의 임플란트를 각각 일렬로 배열되거나, 엇갈리게 배열하였다. 총 120 N 크기의 수직력과 45도 측방력을 가하였고, 유한요소 응력 분석을 시행하였다
결과
측방력 하중에 의해 발생한 최대 응력은 수직력 하중에 의한 것 보다 임플란트 부위에서 3.4 - 5.1배 더 컸고, 지지골 내에서는 3.5 - 8.3배 더 컸다. 모델 M2 의 고정성 보철물의 캔티레버 연결부에서 가장 큰 응력이 집중되었다. 임플란트 개수가 3개인 모델들이 2개인 경우보다 더 낮은 응력이 발생하였으나 M3과 M4에서 일렬 배열과 엇갈린 배열간의 응력 발생 차이는 작았다.
결론
임플란트 배열의 엇갈림 정도는 응력 크기에 별 차이를 발생하지 않았으나, 캔티래버의 존재나 임플란트의 개수의 차이는 큰 영향을 주었다.
Go to :

Keywords: finite element analysis, dental restoration failure, dental stress analysis, implant supported prosthesis, occlusal force
색인어: 유한요소법, 보철 실패, 응력 분석, 임플란트지지 보철, 교합력
Introduction
Because of the absence of periodontal ligaments, osseointegrated implants, unlike natural teeth, react biomechanically in a manner different from occlusal loading. Therefore, dental implants are considered to be prone to occlusal overload. This is considered to be one of the potential causes of bone loss around implant and fracture of implant/implant prosthesis.
1
It has been argued that giving a slight offset to the central implant in a 3-unit implant prosthesis is biomechanically advantageous.
2-4 Marginal bone resorption for implant-supported prostheses with cantilever arms has been reported, and there is concern over excessive stress concentration.
5-7
The purpose of this study was to evaluate effects of loading direction and number of implants in a 3-unit implant support prosthesis with different implant positions on stress distribution in the implant, prosthesis, and the supporting bone based on 3D
finite element analysis.
Go to :

Materials and Methods
Virtual 3D models were geometrically created using CAD (SolidWorks 2018, Dassault Systems, SolidWorks Corporation, Waltham, USA). The CAD model reproduced all characteristics of implant-abutment-prosthesis components of external hexagon connection (USIII CA Ø 4.5 × 13 mm, #AUS3R4513C, cement abutment Ø 5.0/5.5 mm, #CAR525, Osstem Implant, Seoul, Korea) and mandibular edentulous alveolar bone. The alveolar bone was composed of cancellous bone in the center, surrounded by a 1.5 mm-thick cortical bone layer (
Fig. 1).
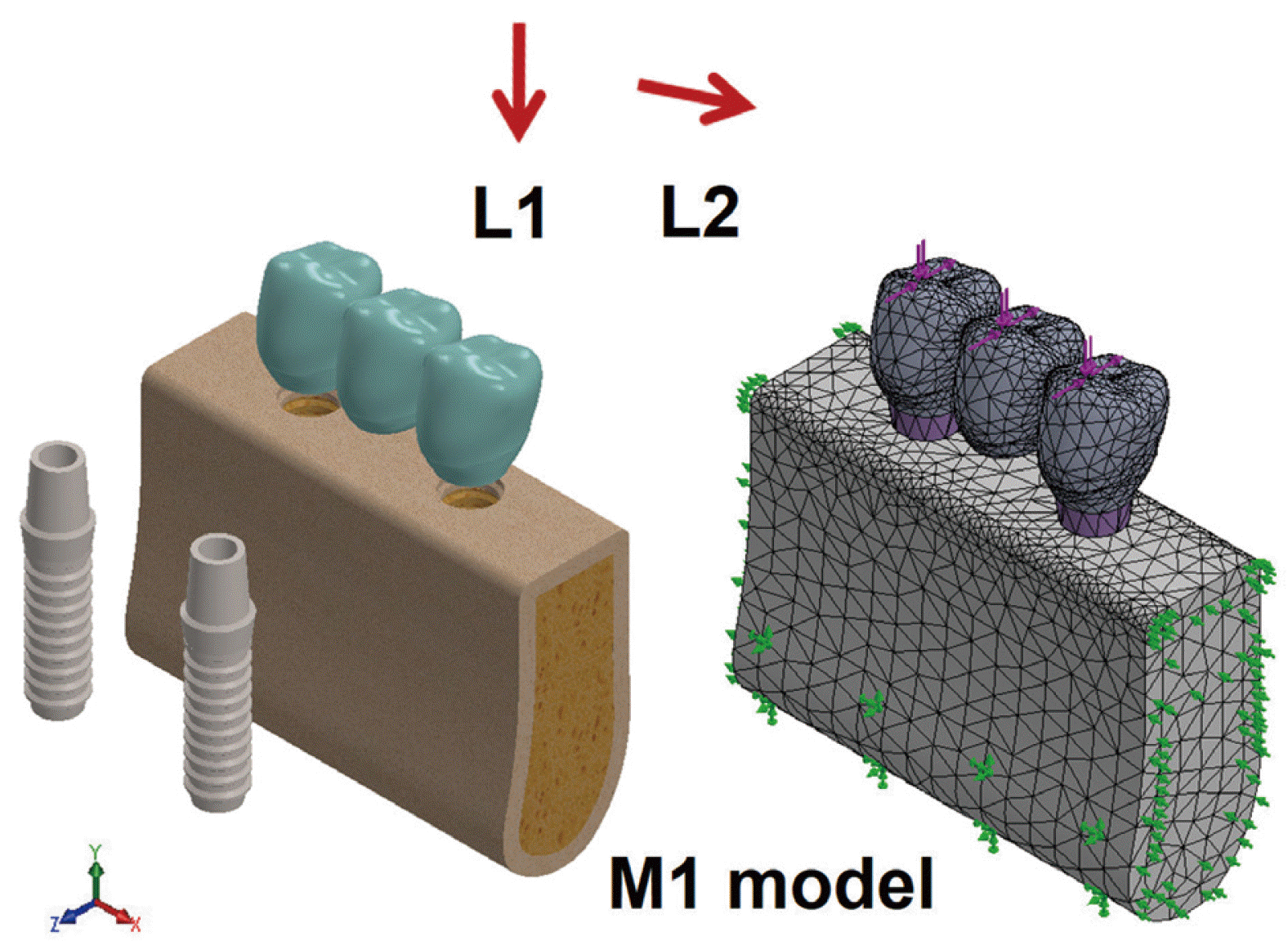 | Fig. 1The M1 model reproduced all characteristics of implant-abutment-prosthesis components and mandibular alveolar bone. Model has meshed with tetrahedral elements. All nodes on the lower surface of the tooth were constrained in all directions (X, Y, and Z), as a boundary condition. Static axial (L1) and 45o lingual directed oblique (L2) force of 120 Newton was applied to the tooth at occlusal contact points respectively. 
|
Four 3D models were used to simulate a posterior mandible bone block: two implants and fixed dental prosthesis (FDP) with a pontic in the center (model M1), two implants and FDP with a cantilever pontic at distal end (model M2), FDP supported by three implants with straight line arrangement (model M3), and FDP supported by three implants with staggered implant configuration (model M4) (
Fig. 2).
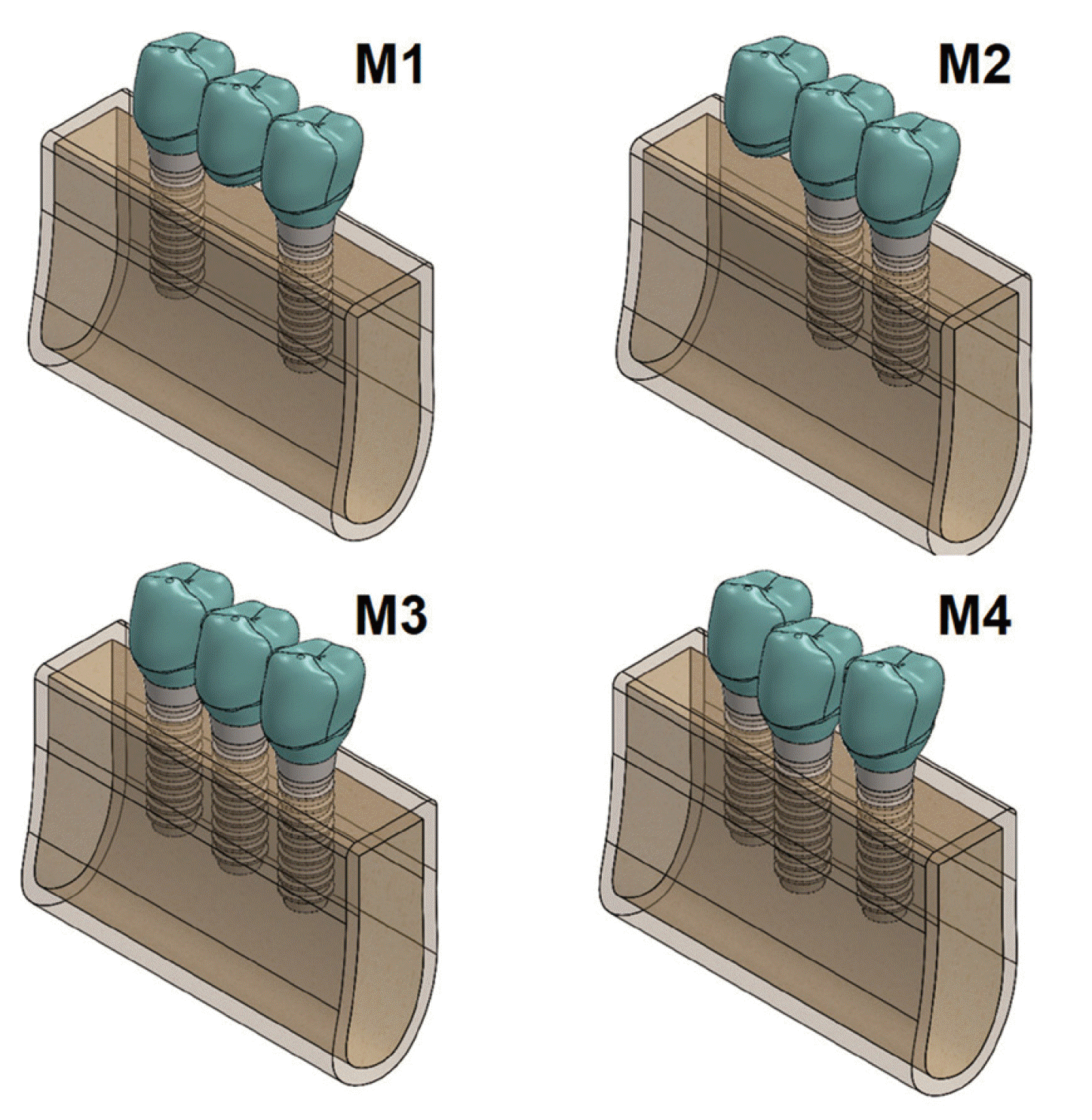 | Fig. 2M1, M2, M3, and M4 models of implant-supported FDPs with various alignments and configurations. 
|
Elastic modulus and Poisson’s ratio of the Y-TZP zirconia and bone were quoted in previous studies.
2,8 Material properties of titanium are obtained from the material database of Solidworks (Dassault Systems, SolidWorks Corporation). Material properties used in this study are listed in
Table 1. All materials were assumed to be linear, elastic, homogeneous, and isotropic. Three-dimensional solid model of M1 has meshed with a tetrahedral solid element (30,539 elements and 47,473 nodes). In order to prevent displacement of the rigid body, fixed boundary conditions of 0-displacement and 0-rotation in all directions (X, Y, and Z) were assigned to the lower mandibular node. We did not allow mesial or distal deformation by assigning 0-displacement boundary conditions to nodes in mesial and distal surfaces of the mandible in the X direction. Contact interfaces between components of the implant were given sliding contact conditions by friction. The friction coefficient of the contact interface between the abut- ment lower part and the upper part of the fixture and that of the contact interface between the screw and the fixture were set to 0.05. In this condition, the contact area carried compressive and friction but not tension. All other contact surfaces of the implant components were considered to be bonded together. Applied forces were 120 N axially (L1), or 120 N obliquely(L2) (
Fig. 1).
Table 1
Materials used in models of fixed dental restoration supported by implant and alveolar bone
|
Young’s modulus |
Poison’s ratio |
|
Y-TZP zirconia |
2.10E + 11 Pa |
0.32 |
|
Ti-6Al-4V |
1.05E + 11 Pa |
0.31 |
|
cp Ti grade |
4 1.05E + 11 Pa |
0.37 |
|
Cortical bone |
1.00E + 10 Pa |
0.30 |
|
Cancellous bone |
1.37E + 09 Pa |
0.30 |

Maximum von Mises and principal stresses on the fixture, abutment, screws, fixed prosthesis, and supporting alveolar bone were calculated and analyzed.
Go to :

Results
Peak von Mises stresses produced by oblique occlusal force were 3.4 - 5.1 times greater in implant and 3.5 - 8.3 times higher in alveolar bone than those produced by axial occlusal force. In the cantilever design of model M2, maximum stress values in the fixed prosthesis caused by vertical and oblique forces were 738.3 and 751.6 MPa, respectively, which were 4.4 and 1.5 times higher than those of model M1, respectively. Stress concentration was observed around the connector region between cantilever pontic and crown. When vertical load was applied, the maximum von Mises stress value in model M4 was 14.7 MPa at the bone. At all parts of the implant, prosthesis, and bone, maximum von Mises stress values in model M4 were lower than those in M1 and M2 models. Stress concentration pattern demonstrated that von Mises stress was maximal around the outer surface of the abutment and a contact interface between abutment and screw. In components of implant, when the maximum stress value generated by oblique force in model M1 was converted to 100%, it increased to 122% in M2, but decreased to 71% and 69% in M3 and M4, respectively (
Table 2,
Fig. 3,
4).
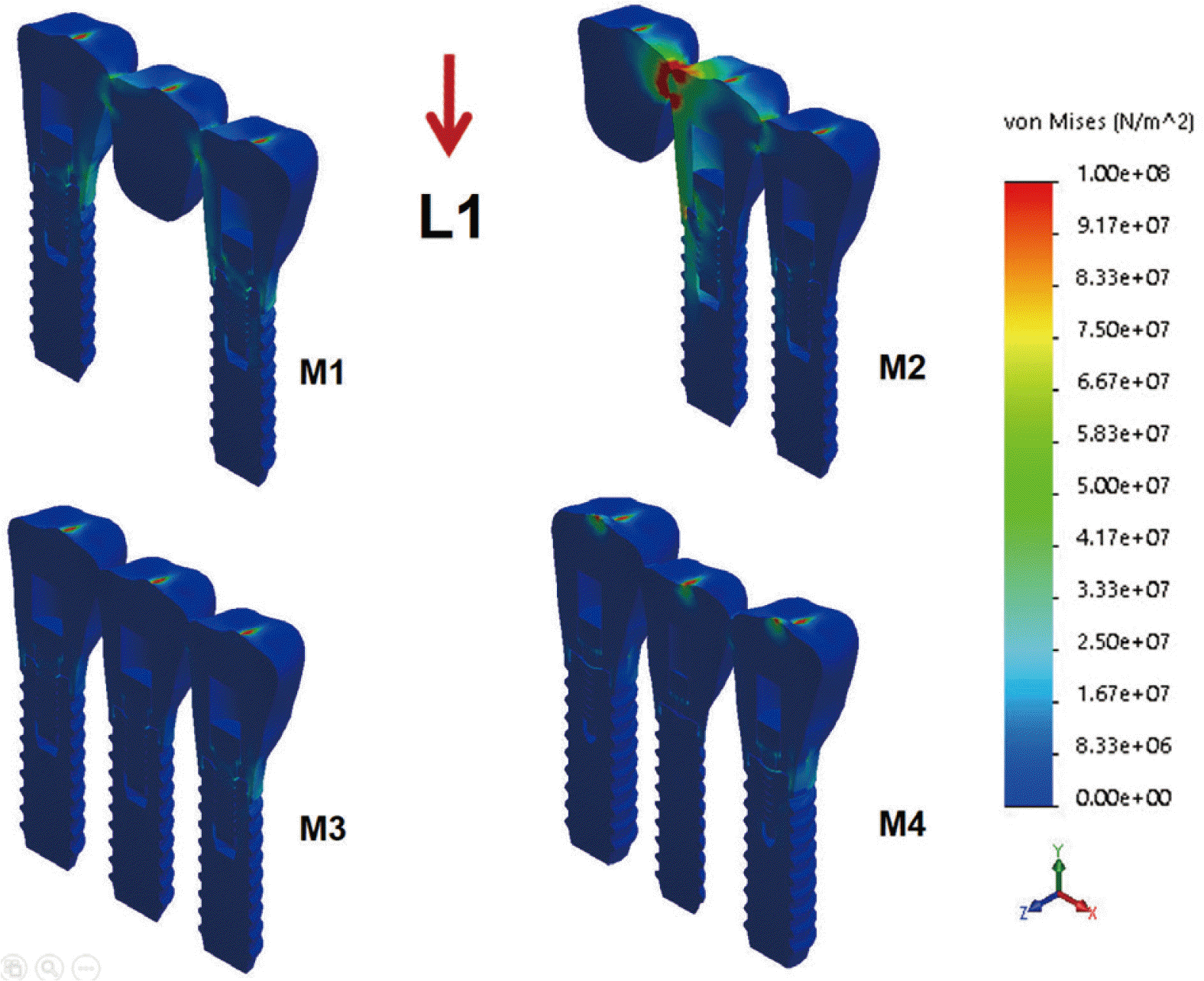 | Fig. 3Maximum von Mises stresses generated in the implant fixture, screw, and abutment of hex external butt connection type by L1 load. Note the peak von Mises stress at the connector region of the cantilever pontic (M2). 
|
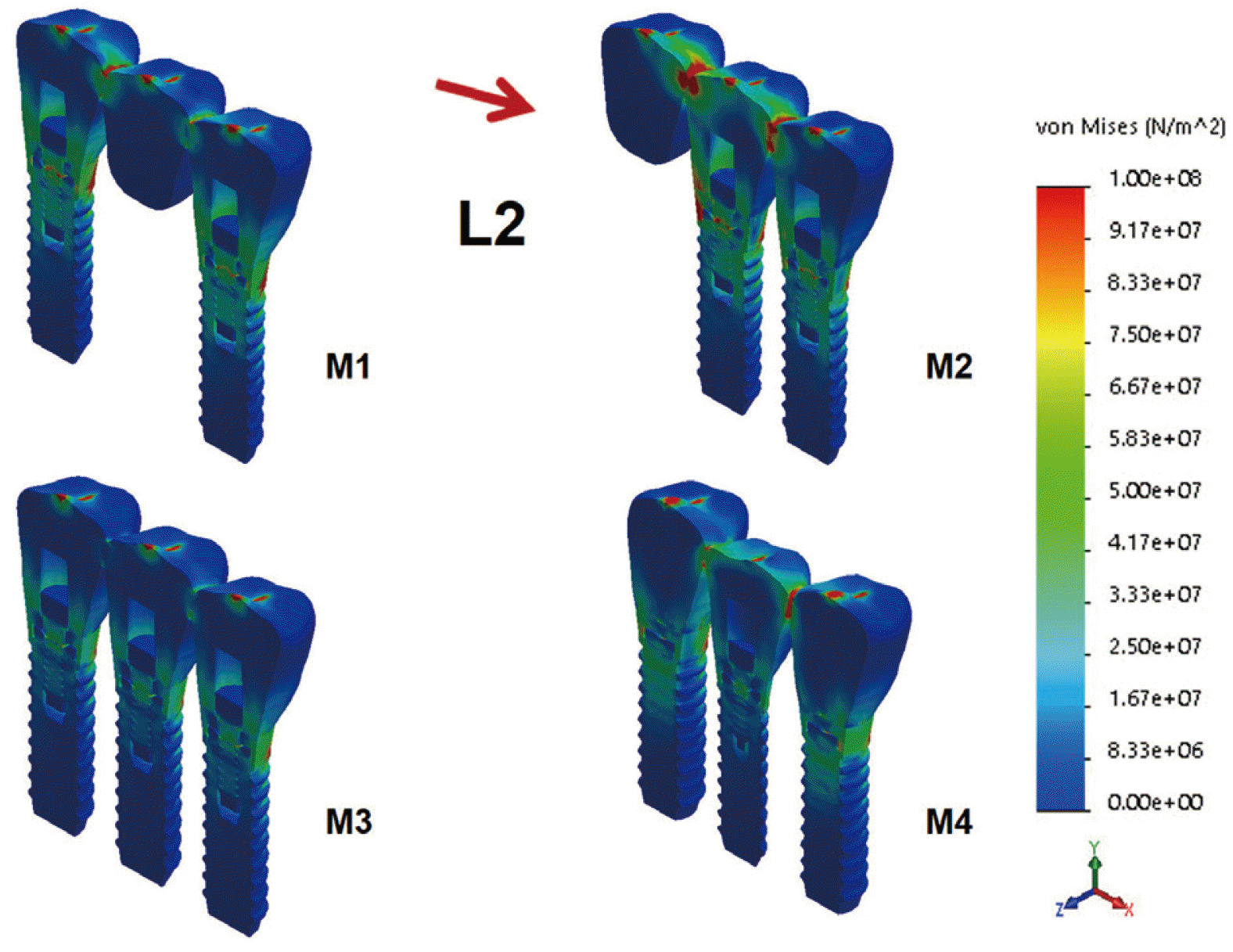 | Fig. 4Maximum von Mises stresses generated in the implant fixture, screw, and abutment by L2 load. Note the peak von Mises stress at the abutment screw by L2. Stress concentration area in the implant was observed at the outer surface of the abutment and a contact interface between abutment and screw. 
|
Table 2
Maximum von Mises stresses generated in implant, FDP and supporting bone by vertical and oblique loadings
|
Model |
Load direction |
Implant |
FDP |
Bone |
|
M1 |
Vertical |
63.6 |
169.2 |
21.3 |
|
Oblique |
327.2 |
516.7 |
165.1 |
|
M2 |
Vertical |
119.3 |
738.3 |
53.0 |
|
Oblique |
399.8 |
751.6 |
187.5 |
|
M3 |
Vertical |
49.1 |
144.2 |
16.9 |
|
Oblique |
231.5 |
373.7 |
123.5 |
|
M4 |
Vertical |
47.9 |
148.6 |
14.7 |
|
Oblique |
227.4 |
315.1 |
121.4 |

In the supporting bone, if the magnitude of principal stress value generated by the oblique load in model M1 was converted to 100%, it increased to 106% in M2, but decreased to 74% and 66% in M3 and M4, respectively. The stress was the highest in the cortical bone at the neck of the implant but the lowest in the cancellous bone. Stress distribution of maximum principal stresses suggested that overloading of the cancellous bone might occur in tension and compression due to the lateral components of an occlusal force. However, a relatively small magnitude of compressive stress was produced at cortical and cancellous bone by vertical loading (
Figs 5 and
6).
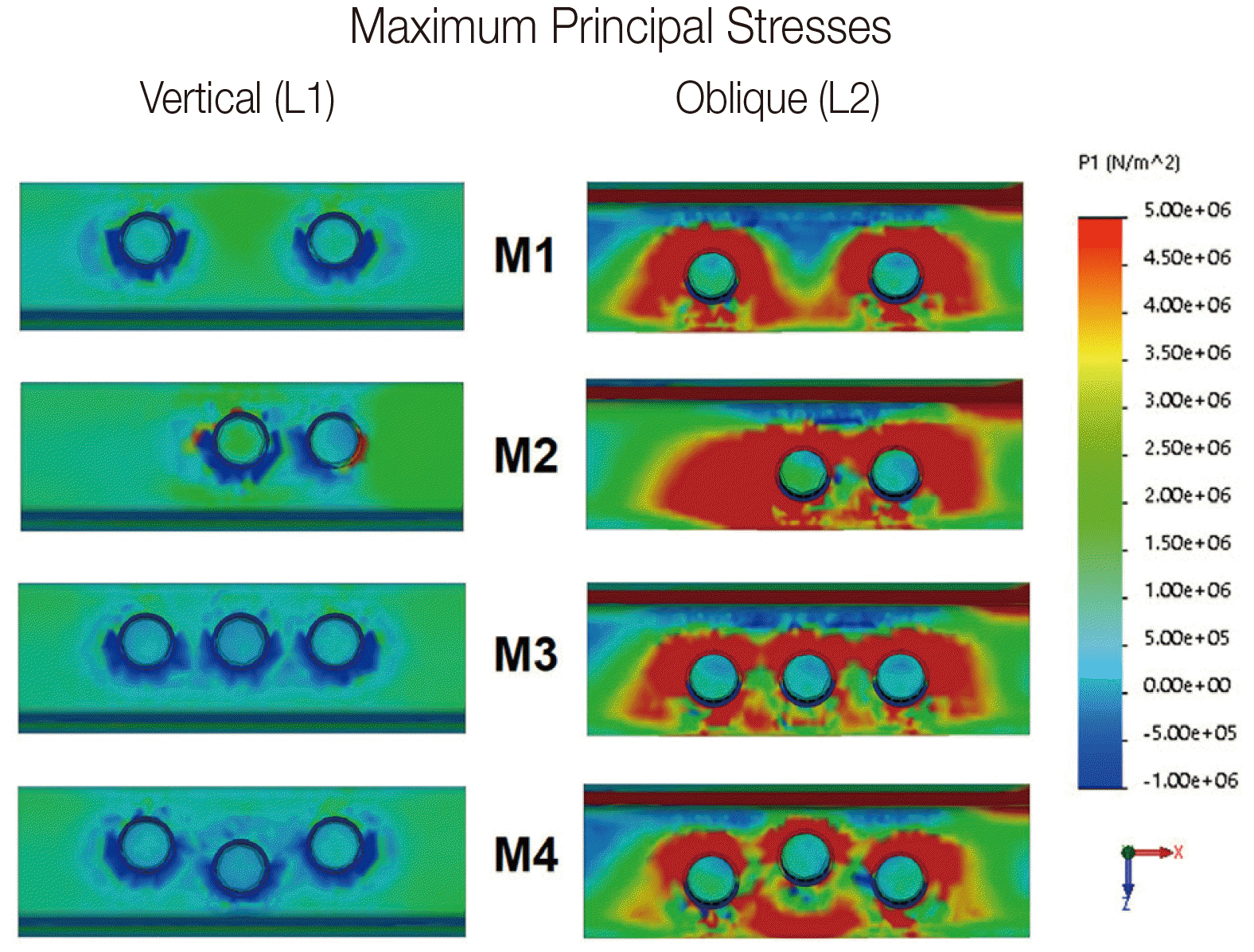 | Fig. 5The magnitude of maximum principal stresses generated in the supporting bone is shown in various colors. The blue color indicates where the compressive force has occurred, and the red color indicates where the tensile force has occurred. 
|
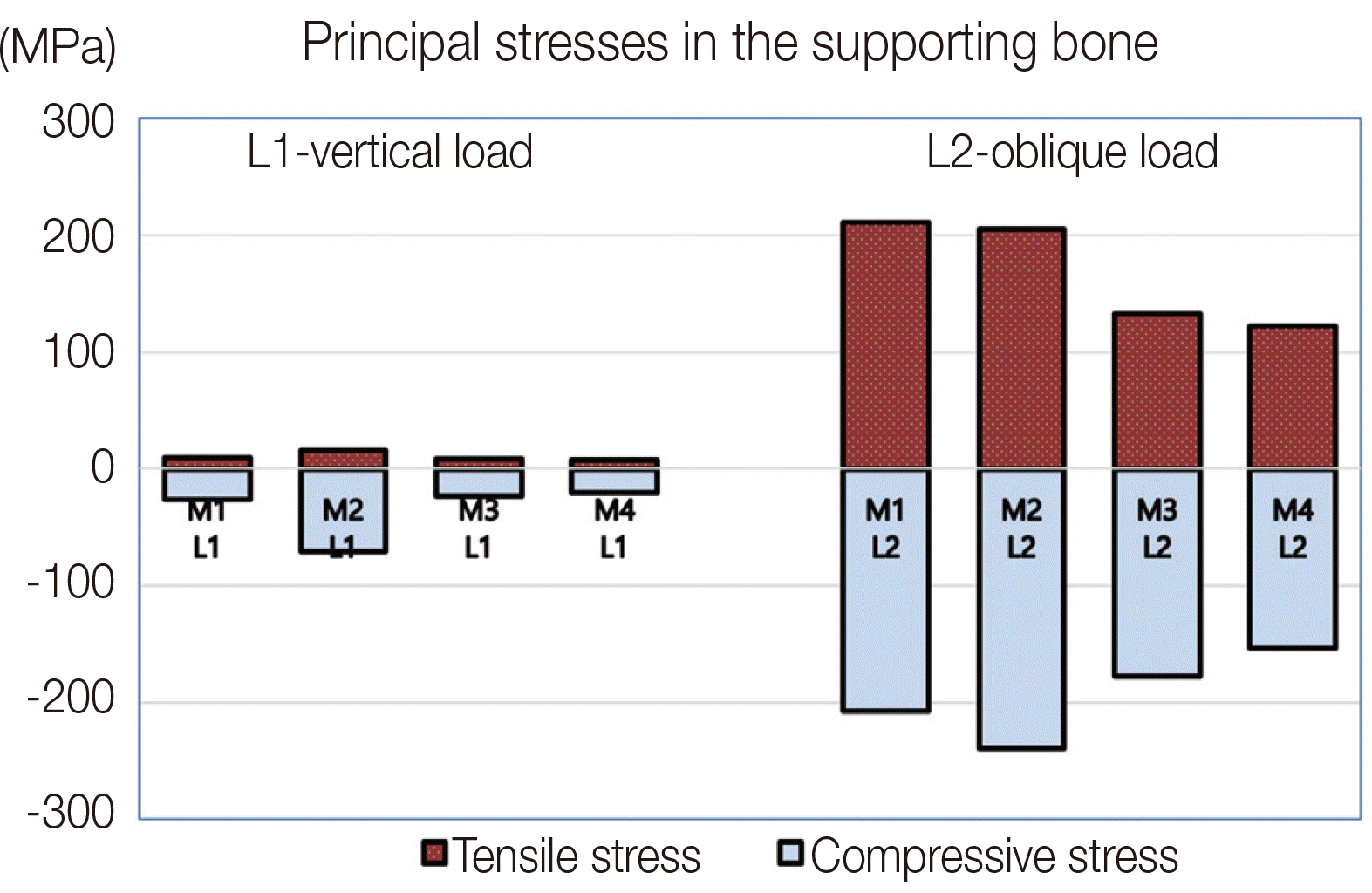 | Fig. 6Model M2 shows the highest principal stress value, while model M4 shows the lowest stress value. Difference in the stress values between the M3 and M4 models was negligible. However, difference between stress values due to vertical load and lateral load was prominent. 
|
Go to :

Discussion
Loosening and fracture of the implant-supported prosthesis are usually associated with overloading on components, especially lateral loading. Peak von Mises stresses produced by oblique occlusal force were 3.4 - 5.1 times greater in implant and 3.5 - 8.3 times higher in alveolar bone than those produced by axial occlusal force. Oblique load increased stress on implants, prosthesis, and bone tissue in our study. This is consistent with findings of recent studies
5,9 showing increased stress in implant and supporting bone under oblique loads. The general concept of ideal occlusion, which requires the application of biting force in the long axis of the tooth, was also confirmed by finite element analysis of implant-supported fixed prostheses in this study.
There have been many conflicting claims and research reports
2-4,10 on biomechanical implications of staggering implant arrangement. Only one offset distance from the straight alignment (1.8 mm) was analyzed in the present study. When oblique occlusal force was applied, offset arranfement of model M4 generated 227.4, 315.1 and 121.4 MPa maximum von Mises stresses in implant, prosthesis and alveolar bone, respectively, which were almost same as those of straight arrangement of model M3 (
Table 2). The effect of staggering alignment on implant stress was negligible when compare to the effect of load direction. Sato et al.
3 suggested that offset implants were loaded with 59 - 65% compared to controls from geometric analysis. In 1997, Langert et al.,
10 based on theoretical assumptions, proposed the biomechanical benefit of staggered placement to reduce stresses of implant. The previous literature’s
3,10 assumption, which were not performed the laboratory analysis, that offset implant configuration is advantageous, was not validated by the results of this finite element analysis. Our results were consistent with the other FEA results of Huang et al.,
4 who demonstrate the maximum stress in the alveolar bone around each implant did not show a difference between the straight- line and offset implant configurations. According to our research results, placing the multiple implants along the line of the dental arch is more advantageous than the staggered placement of the implant, considering the esthetic and oral hygiene care aspects. The maximum stress generated by the M1 model, which was supported by two implants was 152% higher than the M4 model, which was supported by three implants. The difference in maximum stress generated by the alignment of the implant placement (between M3 and M4) was negligible. The number of implants installed (between M1 and M4) had a greater impact than implant alignment (
Table 2,
Fig. 5).
Many systematic reviews
11,12 have shown that short span FDPs with cantilever extensions represent a predictable treatment. Results of the present study showed that the cantilever design associated with implant support FDP slightly increased the stress in the alveolar bone. However, by showing a high stress concentration in the connector part of the FPD, fracture of the FPD may occur (
Fig. 4,
5). The load should be avoided on cantilever portion to decrease the risk of fracture.
Results of the present study confirmed that the risk of bone overload essentially affected regions around the implant neck. Clinically, it has been reported that loss of marginal bone mainly starts around the im- plant neck and progresses to the deep bone at a later stage (
Fig. 5).
6
Finite element analysis is based on mathematical calculations. Living tissues are beyond confines of set parameters and values since biology is not a comput- able entity.
9 Therefore, finite element analysis should not be considered as the only means to understand the behavior of geometric structures in a given value. Clinical trials should be performed after finite element analysis for final validation with biological systems.
Go to :

Conclusion
Peak von Mises stresses observed in implants pro- duced by oblique occlusal force were 3.4 - 5.1 times higher in implant and 3.5 - 8.3 times higher in alveo- lar bone than such stresses produced by axial occlusal force.
When the peak von Mises stress value of the im- plant generated by oblique force in model M1 was converted to 100%, it increased to 122% in M2, but decreased to 71% and 69% in M3 and M4, respec- tively.
In the supporting bone, when the maximum value of principal stress produced by oblique force in model M1 was converted to 100%, it increased to 106% in M2, but decreased to 74% and 66% in M3 and M4, respectively.
The effect of staggering alignment on implant stress was negligible. However, the number of im- plants installed had a more significant impact on
stress.
Go to :








 PDF
PDF Citation
Citation Print
Print






 XML Download
XML Download