Abstract
Purpose
The purpose of this study was to compare the biomechanical outcome in the mandibular posterior region between two different loading conditions by finite element analysis.
Materials and Methods
The mandibular posterior teeth model and the implant model were generated for the study. And 2 different types of loading conditions were provided: Arbitrary occlusion and natural occlusion obtained from the digital occlusal analyzer, Accura (Accura, Dmetec Co. Ltd., Seoul, Korea). Total load of 100 N was evenly distributed over arbitrary occlusion points, and 100 N load was differentially distributed over natural occlusion points according to Accura data. The biomechanical outcome was evaluated by the finite element analysis software.
Finite element analysis method has been adopted as a useful tool to analyze the biomechanical characteristics of oral system. This method provides in-depth, three-dimensional pattern of the stress distribution which would have been otherwise difficult to implement and observe.1-4 As such, the stress generated by occlusal load in various experimental modalities has been studied. However, some studies5-13 have pointed out that occlusion may have significant effect on the result of finite element analysis which means that the three-dimensional location and direction of the occlusion itself could be a variable that can change the stress distribution.
Benazzi et al.7 compared the stress distribution of a premolar under different loading conditions. Arbitrary occlusal points on buccal cusp tip, center point of mesio-distal groove, and buccal cusp tip with 45-degree angle from the tooth axis were given to each three identical premolar model. The occlusal area from the early time frame during mastication that was projected by software was chosen and given to another identical premolar model. In addition, the occlusal area during maximum intercuspation was used. The result of those 5 models showed different stress distribution patterns. The authors stated that the loading direction and position can affect the result of finite element analysis and nevertheless, there is a tendency to simplify the force parameter in most of the studies. Brune et al.8 investigated the stress distribution of a single implant crown buried in a bone block simulating the bone-implant osseointegration. Different occlusal setups were prepared as three occlusal contact areas and five occlusal areas. In addition, different cuspal angles were given as another variable. Load was applied in the same direction of the implant longitudinal axis with the magnitude of 100 N. The authors observed the difference in the pattern and intensity of the stress distribution under the same load. Röehrle et al.9 questioned the validity of the finite element analysis that adopted arbitrary point loads as force parameter since point loads are not the physiologic conditions.
However, upon review of the literatures, it seems that the occlusal load configuration has not been dealt as an important factor. Rather, many studies have implied arbitrary or simplified occlusal points on their study.14-19 A newly developed digital occlusal analyzer, Accura, is capable of providing the geographic information of the occlusal area imprinted during mastication.20 The Accura is a piezoelectric sensor that converts the occlusal load into varying degree of electrical charge which then can be calibrated to identify the magnitude of occlusal load. The Accura is capable of recording the masticatory force in 256 levels. The accura film sensor consists of 1,172 to 1,390 piezoelectric sensels and the location of the activated sensels can be used to determine the position of the occlusal contacts.
The purpose of this study was to compare the results of the finite element analyses under two different loading conditions; arbitrary occlusion and the realistic occlusion obtained from Accura.
A left side mandibular hemisectioned mandibular model with teeth and bone (Fig. 1) was obtained from the subject’s cone-beam computed tomography record with informed consent and was used as a template to create the mesh model for finite element analysis. Different layers of the model such as the cortical bone, cancellous bone, enamel, dentin, and periodontal ligament were segmented using the three-dimensional design software (Mimics, Materialise NV, Leuven, Belgium). Those layers were converted into mesh models using the mesh generation software (Visual-Mesh, ESI Group, Paris, France). The thickness of the periodontal ligament was evenly provided as 0.2 mm according to previous studies21-23 and assembled with the rest of the layers.
The second model was identical to the first model except that posterior teeth were replaced with implants. The implants were embedded in the model at the height of the alveolar bone crest, and positioned as the center long axis of the implants to aim the central fossa of the occlusal surface. The geometry of occlusal table remained identical compared to the first model. The geometry of the implant system (Osstem GS, Osstem Implant Co., Ltd., Seoul, Korea) was provided by the manufacturer. The meshes for crowns were created and assembled together with other restorative components such as the abutment and screw.
Two types of occlusions were used for the experiment. For the arbitrary occlusion, multiple arbitrary points were designated at the functional cusps and fossae (Fig. 2), whereas for the natural occlusion, the occlusal data obtained from Accura digital occlusal analyzer (Accura, Dmetec Co. Ltd., Seoul, Korea) during maximum intercuspal position was used by superimposition of the Accura data and model geometry (Fig. 3). The Accura occlusion data was obtained from the same subject who provided the mandibular model. In total, four experimental setups were planned as listed in Table 1. Natural teeth model with arbitrary occlusion (NA), natural teeth model with natural occlusion (NN), implant model with arbitrary occlusion (IA), and implant model with natural occlusion (IN).
The parameters of material properties used in this study were acquired from other studies23-33 as described in Table 2. The material conditions were assumed to be homogeneous, isotropic, and linear. The friction contact was applied as the interface condition between implant components and the friction coefficient was 0.3.34,35 It was assumed that the bone-to-implant contact ratio was 100%.1,36,37
The magnitude of 100 N load was provided according to the occlusion setup. The directions of applied load were oblique to the long axis of natural teeth or implants by ratio of horizontal axis versus vertical axis as 1:5. For the arbitrary occlusion setup, 100 N load was equally distributed to every occlusal point whereas for the natural occlusion setup, the 100 N load was differentially distributed according to the Accura bite force information. Preload of gold screw was set as 664 N.38.39 All those properties and restrictions were defined using the pre-processor software (Visual-Crash for PAM, ESI Group). The finite element analysis was performed using the solver software (Solver Launcher, ESI Group). The outcome value of maximum von Mises stress and the amount of displacement was observed for the evaluation.
The maximum von Mises stress values measured from experimental models are listed in Table 3. There was considerable difference in stress value within natural teeth model with different occlusion setup (NA, NN). The location of the maximum von Mises stress was similarly at the apex of 2nd premolar area in both occlusion setups. Unlike natural teeth models, implant models (IA, IN) showed relatively small difference in maximum von Mises stress value between the arbitrary and natural occlusion. Both occlusion setups showed similar location of maximum von Mises stress which was at the fixture screw of 2nd premolar implant.
The maximum von Mises stress values measured at each of the components are listed in Table 4. In natural teeth models, the maximum stress values of individual components were quite different between both occlusion setups. However, implant models showed relatively small difference in terms of maximum stress values on individual components between arbitrary and natural occlusion setups. The differences in values did not exceed 10% of greater values. The graphic demonstration of von Mises stress distribution pattern of different models are shown in Fig. 4.
The maximum displacement values and locations are listed in Table 5. The displacement value of natural teeth models differed according to occlusal setups. The location where maximum displacement occurred was also different. In arbitrary occlusion, 1st premolar buccal surface was most vulnerable to displacement while in natural occlusion, it was 2nd molar buccal surface. In implant models, the maximum displacement values differed considerably as well as their location of maximum displacement. It was 1st premolar fixture screw area where maximum displacement occurred in the pearbitrary occlusion setup model (IA) whereas it was 1st molar fixture screw area for the natural occlusion setup model (IN).
It was shown that different occlusal patterns lead to different results in terms of the stress distribution and displacement. This result was in agreement with other studies that indicated different loading pattern to have significant influence on the stress distribution and subsequent outcome analysis.5-13 Therefore, providing an arbitrary loading condition for finite element analysis will have to be avoided as its result may not be close to real situation, especially when the study is aiming for a quantitative analysis of individual structure.
There was a tendency that natural occlusion setup models (NN, IN) showed greater maximum von Mises stress and maximum displacement than arbitrary occlusion setup models (NA, IA) despite the greater numbers in occlusal points in arbitrary occlusion setup. It could be attributed to the differential load distribution in natural occlusion setup models. The concentrated load resulted in greater stress and distribution. In addition, the locations of maximum von Mises stress of each models remained constant throughout different occlusion setups. However, different occlusion setups lead to change in the locations of maximum displacement.
Accura is developed as a digitalized occlusion measurement device with the capability of real-time measurement and data record.20 Its capability includes not only recording the occlusal point and force, but also the timing of the occlusion. Therefore, it can provide accurate individual occlusion data for the computer simulation such as finite element analysis or occlusal measurement related quantitative study. Further development of this device into a necessary equipment in various dynamic analysis including computer simulation is expected.
The results of the present study showed that the variations in outcome were considerable and could not be considered as negligible. It can be assumed that the result of a single experimental modality may only represent a single situation and cannot be applied as a universal interpretation of biomechanical behavior. The biomechanics of a treatment protocol can be affected by various factors, especially occlusal pattern, and therefore, its clinical performance prediction via finite element study may only deserve for limited validity. Based on the result of this study, it would be highly desirable in finite element analysis that various loading conditions both in terms of magnitude and distribution to be provided for realistic prediction of the results. Yet, there is little information regarding the sufficient range of various loading conditions to cover the real clinical situations. Further studies would be required to decide the sufficient range of various loading conditions and occlusion in order to raise the predictability of finite element analysis in dentistry.
Different occlusal loading conditions lead to different stress distribution pattern. The Arbitrary occlusion and realistic occlusion that was acquired from Accura showed considerably different result in terms of maximum von Mises stress and maximum displacement level.
In finite element analysis, it is recommended to simulate with occlusal contact point and force that are based on accurate measurement.
Acknowledgements
This work was supported by SNU Brain Fusion Program of the Seoul National University in 2016. This work was supported by the Seoul National University Research Grant in 2016.
References
1. Geng JP, Tan KB, Liu GR. 2001; Application of finite element analysis in implant dentistry: a review of the literature. J Prosthet Dent. 85:585–98. DOI: 10.1067/mpr.2001.115251. PMID: 11404759.
2. DeTolla DH, Andreana S, Patra A, Buhite R, Comella B. 2000; Role of the finite element model in dental implants. J Oral Implantol. 26:77–81. DOI: 10.1563/1548-1336(2000)026<0077:TROTFE>2.3.CO;2.
3. Trivedi S. 2014; Finite element analysis: a boon to dentistry. J Oral Biol Craniofac Res. 4:200–3. DOI: 10.1016/j.jobcr.2014.11.008. PMID: 25737944. PMCID: PMC4306993.
4. Shetty P, Hegde AM, Rai K. 2010; Finite element method-an effective research tool for dentistry. J Clin Pediatr Dent. 34:281–5. DOI: 10.17796/jcpd.34.3.yu44334815546435. PMID: 20578669.
5. Eskitascioglu G, Usumez A, Sevimay M, Soykan E, Unsal E. 2004; The influence of occlusal loading location on stresses transferred to implant-supported prostheses and supporting bone: a three-dimensional finite element study. J Prosthet Dent. 91:144–50. DOI: 10.1016/j.prosdent.2003.10.018. PMID: 14970760.
6. Hernández-Vázquez RA, Romero-Ángeles B, Urriolagoitia-Sosa G, Vázquez-Feijoo JA, Vázquez-López ÁJ, Urriolagoitia-Calderón G. 2018; Numerical analysis of masticatory forces on a lower first molar considering the contact between dental tissues. Appl Bionic Biomech. 2018:4196343. DOI: 10.1155/2018/4196343. PMID: 29849758. PMCID: PMC5914157.
7. Benazzi S, Grosse IR, Gruppioni G, Weber GW, Kullmer O. 2014; Comparison of occlusal loading conditions in a lower second premolar using three-dimensional finite element analysis. Clin Oral Investig. 18:369–75. DOI: 10.1007/s00784-013-0973-8. PMID: 23504207.
8. Brune A, Stiesch M, Eisenburger M, Greuling A. 2019; The effect of different occlusal contact situations on peri-implant bone stress - a contact finite element analysis of indirect axial loading. Mater Sci Eng C Mater Biol Appl. 99:367–73. DOI: 10.1016/j.msec.2019.01.104. PMID: 30889710.
9. Röehrle O, Saini H, Ackland DC. 2018; Occlusal loading during biting from an experimental and simulation point of view. Dent Mater. 34:58–68. DOI: 10.1016/j.dental.2017.09.005. PMID: 29017762.
10. Chang Y, Tambe AA, Maeda Y, Wada M, Gonda T. 2018; Finite element analysis of dental implants with validation: to what extent can we expect the model to predict biological phenomena? A literature review and proposal for classification of a validation process. Int J Implant Dent. 4:7. DOI: 10.1186/s40729-018-0119-5. PMID: 29516219. PMCID: PMC5842167.
11. De Jager N, de Kler M, van der Zel JM. 2006; The influence of different core material on the FEA-determined stress distribution in dental crowns. Dent Mater. 22:234–42. DOI: 10.1016/j.dental.2005.04.034. PMID: 16099031.
12. Kondo T, Wakabayashi N. 2009; Influence of molar support loss on stress and strain in premolar periodontium: a patient-specific FEM study. J Dent. 37:541–8. DOI: 10.1016/j.jdent.2009.03.015. PMID: 19380187.
13. Rand A, Stiesch M, Eisenburger M, Greuling A. 2017; The effect of direct and indirect force transmission on peri-implant bone stress - a contact finite element analysis. Comput Methods Biomech Biomed Engin. 20:1132–9. DOI: 10.1080/10255842.2017.1338691. PMID: 28622020.
14. Cailleteau JG, Rieger MR, Akin JE. 1992; A comparison of intracanal stresses in a post-restored tooth utilizing the finite element method. J Endodont. 18:540–4. DOI: 10.1016/S0099-2399(06)81210-0.
15. Papavasiliou G, Kamposiora P, Bayne SC, Felton DA. 1996; Three-dimensional finite element analysis of stress-distribution around single tooth implants as a function of bony support prosthesis type and loading during function. J Prosthet Dent. 76:633–40. DOI: 10.1016/S0022-3913(96)90442-4.
16. Ausiello P, Apicella A, Davidson CL. 2002; Effect of adhesive layer properties on stress distribution in composite restorations - a 3D finite element analysis. Dent Mater. 18:295–303. DOI: 10.1016/S0109-5641(01)00042-2.
17. Eskitascioglu G, Usumez A, Sevimay M, Soykan E, Unsal E. 2004; The influence of occlusal loading location on stresses transferred to implant-supported prostheses and supporting bone: a three-dimensional finite element study. J Prosthet Dent. 91:144–50. DOI: 10.1016/j.prosdent.2003.10.018. PMID: 14970760.
18. Lanza A, Aversa R, Rengo S, Apicella D, Apicella A. 2005; 3D FEA of cemented steel glass and carbon posts in a maxillary incisor. Dent Mater. 21:709–15. DOI: 10.1016/j.dental.2004.09.010. PMID: 16026666.
19. Mozayek RS, Allaf M, Abuharb MB. 2016; Efficacy of adding a supporting implant in stress distribution of long-span fixed partial dentures: a 3D finite element analysis. J Dent Res Dent Clin Dent Prospects. 10:81–6. DOI: 10.15171/joddd.2016.013. PMID: 27429723. PMCID: PMC4946000.
20. Jeong MY, Lim YJ, Kim MJ, Kwon HB. 2020; Comparison of two computerized occlusal analysis systems for indicating occlusal contacts. J Adv Prosthodont. 12:49–54. DOI: 10.4047/jap.2020.12.2.49. PMID: 32377316. PMCID: PMC7183850.
21. Coolidge ED. 1937; The thickness of the human periodontal membrane. J Am Dent Assoc. 24:1260–70. DOI: 10.14219/jada.archive.1937.0229.
22. Yoshida N, Koga Y, Peng CL, Tanaka E, Kobayashi K. 2001; In vivo measurement of the elastic modulus of the human periodontal ligament. Med Eng Phy. 23:567–72. DOI: 10.1016/S1350-4533(01)00073-X.
23. Cattaneo PM, Dalstra M, Melsen B. 2005; The finite element method: a tool to study orthodontic tooth movement. J Dent Res. 84:428–33. DOI: 10.1177/154405910508400506. PMID: 15840778.
24. Moroi HH, Okimoto K, Moroi R, Terada Y. 1993; Numeric approach to the biomechanical analysis of thermal effects in coated implants. Int J Prosthodont. 6:564–72.
25. Sano H, Ciucchi B, Matthews WG, Pashley DH. 1994; Tensile properties of mineralized and demineralized human and bovine dentin. J Dent Res. 73:1205–11. DOI: 10.1177/00220345940730061201. PMID: 8046110.
26. Farah JW, Craig RG, Meroueh KA. 1989; Finite element analysis of three- and four-unit bridges. J Oral Rehabil. 16:603–11. DOI: 10.1111/j.1365-2842.1989.tb01384.x. PMID: 2689617.
27. Jones ML, Hickman J, Middleton J, Knox J, Volp C. 2001; A validated finite element method study of orthodontic tooth movement in the human subject. J Orthod. 28:29–38. DOI: 10.1093/ortho/28.1.29. PMID: 11254801.
28. Tanne K, Yoshida S, Kawata T, Sasaki A, Knox J, Jones ML. 1998; An evaluation of the biomechanical response of the tooth and periodontium to orthodontic forces in adolescent and adult subjects. Br J Orthod. 25:109–15. DOI: 10.1093/ortho/25.2.109. PMID: 9668993.
29. Toms SR, Eberhardt AW. 2003; A nonlinear finite element analysis of the periodontal ligament under orthodontic tooth loading. Am J Orthod Dentofacial Orthop. 123:657–65. DOI: 10.1016/S0889-5406(03)00164-1.
30. Jung WK, Lee WS, Kwon HB. 2019; Effects of abutment screw preload in two implant connection systems: a 3D finite element study. J Prosthet Dent. 122:474.e1–e8. DOI: 10.1016/j.prosdent.2019.04.025. PMID: 31590980.
31. Silva GC, Cornacchia TM, de Magalhães CS, Bueno AC, Moreira AN. 2014; Biomechanical evaluation of screw-and cement-retained implant-supported prostheses: a nonlinear finite element analysis. J Prosthet Dent. 112:1479–88. DOI: 10.1016/j.prosdent.2014.06.010. PMID: 25062583.
32. Quaresma SET, Cury PR, Sendyk WR, Sendyk C. 2008; A finite element analysis of two different dental implants: stress distribution in the prosthesis, abutment, implant, and supporting bone. J Oral Implantol. 34:1–6. DOI: 10.1563/1548-1336(2008)34[1:AFEAOT]2.0.CO;2.
33. Wataha JC. 2002; Alloys for prosthodontic restorations. J Prosthet Dent. 87:351–63. DOI: 10.1067/mpr.2002.123817. PMID: 12011845.
34. Jörn D, Kohorst P, Besdo S, Rücker M, Stiesch M, Borchers L. 2014; Influence of lubricant on screw preload and stresses in a finite element model for a dental implant. J Prosthet Dent. 112:340–8. DOI: 10.1016/j.prosdent.2013.10.016. PMID: 24529658.
35. Inzana JA, Varga P, Windolf M. 2016; Implicit modeling of screw threads for efficient finite element analysis of complex bone-implant systems. J Biomech. 49:1836–44. DOI: 10.1016/j.jbiomech.2016.04.021. PMID: 27157243.
36. Hsu ML, Chen FC, Kao HC, Cheng CK. 2007; Influence of off-axis loading of an anterior maxillary implant: a 3-dimensional finite element analysis. Int J Oral Maxillofac Implants. 22:301–9. DOI: 10.1016/S0021-9290(06)85337-6. PMID: 17465356.
37. Chang CL, Chen CS, Huang CH, Hsu ML. 2012; Finite element analysis of the dental implant using a topology optimization method. Med Eng Phys. 34:999–1008. DOI: 10.1016/j.medengphy.2012.06.004. PMID: 22770748.
38. Martin WC, Woody RD, Miller BH, Miller AW. 2011; Implant abutment screw rotations and preloads for four different screw materials and surfaces. J Prosthet Dent. 86:24–32. DOI: 10.1067/mpr.2001.116230. PMID: 11458261.
39. Lang LA, Kang B, Wang RF, Lang BR. 2003; Finite element analysis to determine implant preload. J Prosthet Dent. 90:539–46. DOI: 10.1016/j.prosdent.2003.09.012. PMID: 14668754.
Fig. 1
Mesh models generated for finite element analysis. (A) Natural teeth model which consist of the mandibular cortical bone, cancellous bone, periodontal ligament, and teeth, (B) Implant model which consist of the mandibular cortical bone, cancellous bone, implant, abutment screw, abutment, and crown.
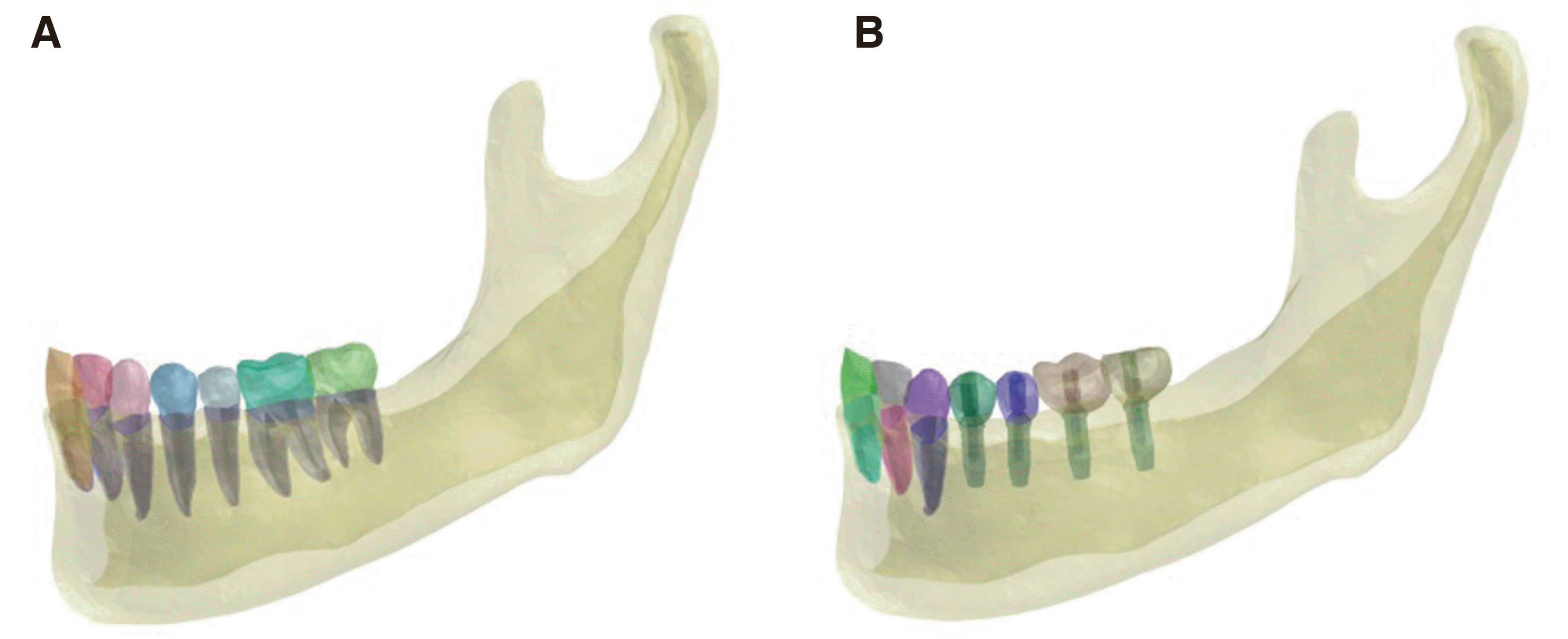
Fig. 2
Arbitrary occlusion setup. Yellow points are arbitrary occlusal points designated on premolar and molar region.
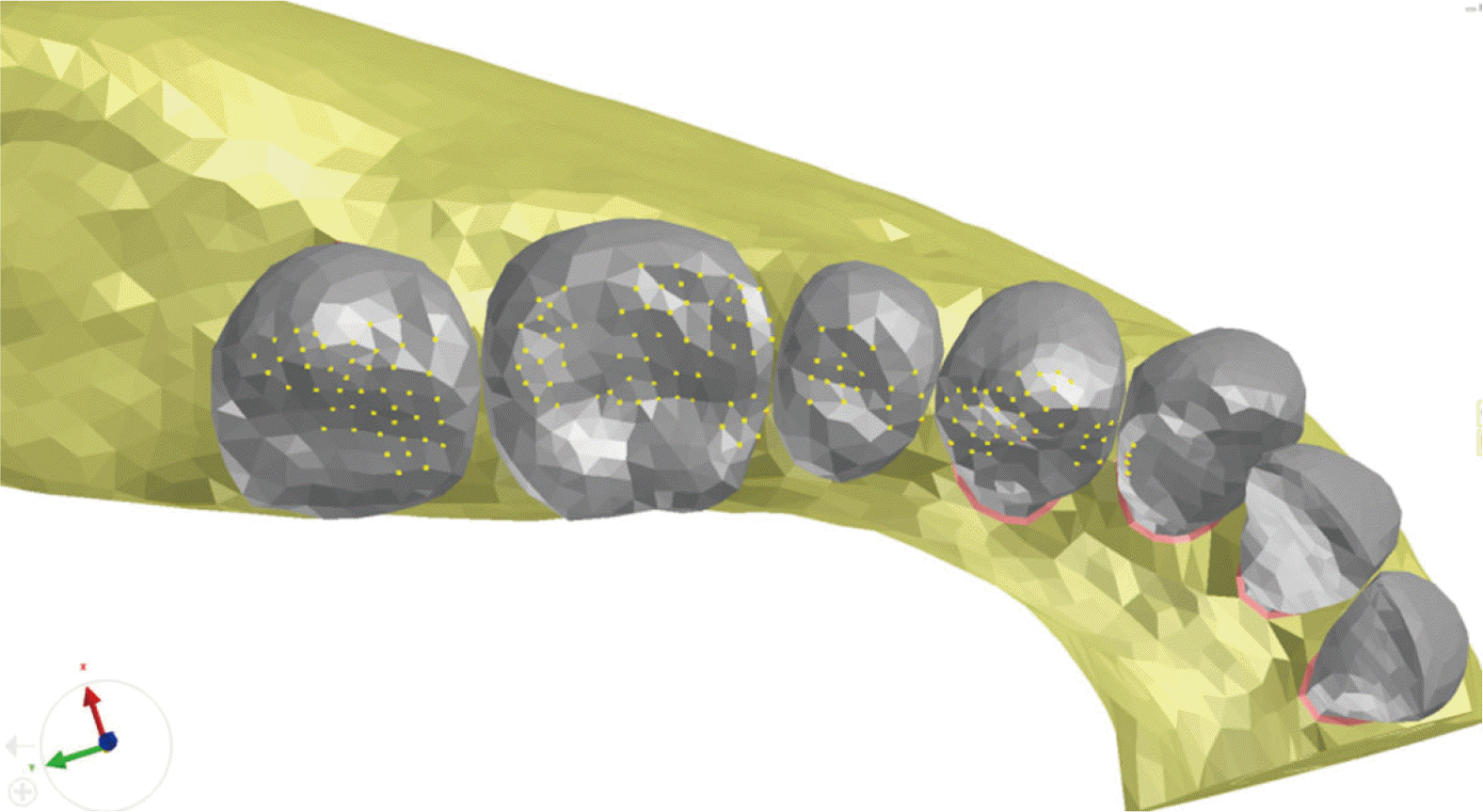
Fig. 3
Natural occlusion setup. (A) Natural occlusion data acquisition by Accura, (B) Based on natural occlusion data, occlusal points were determined by superimposition of Accura data and model geometry.
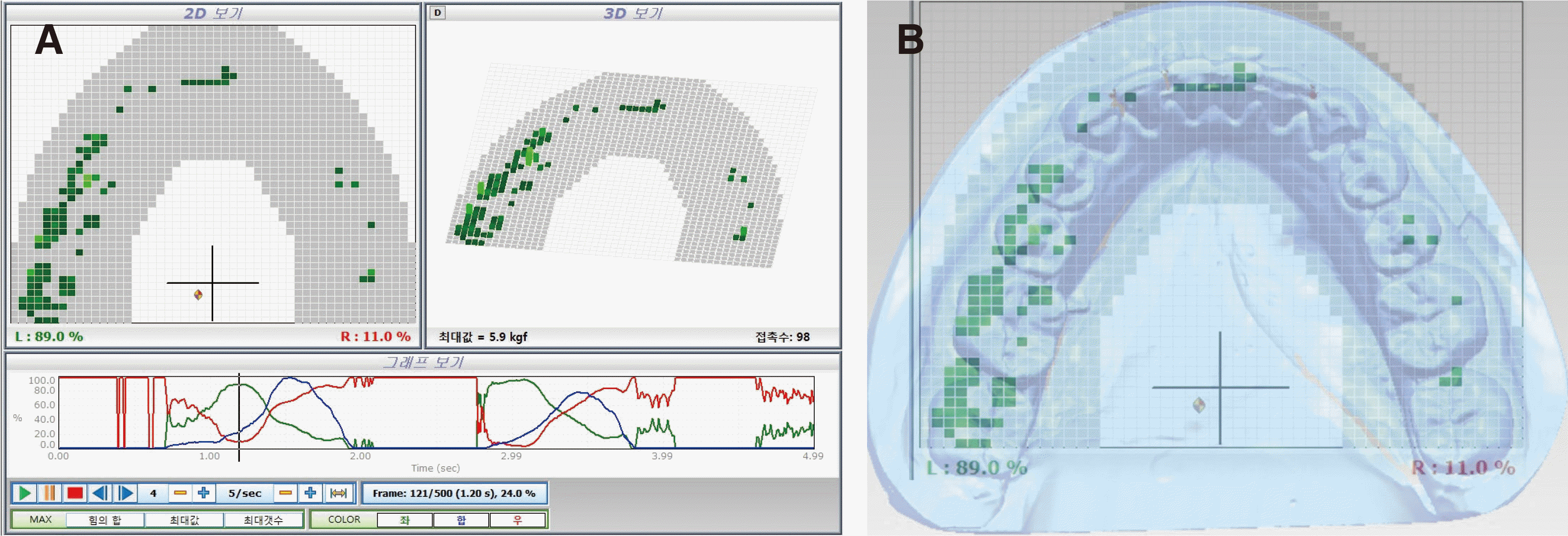
Fig. 4
Von Mises stress distribution pattern. (A) NA model, (B) NN model, (C) IA model, (D) IN model.
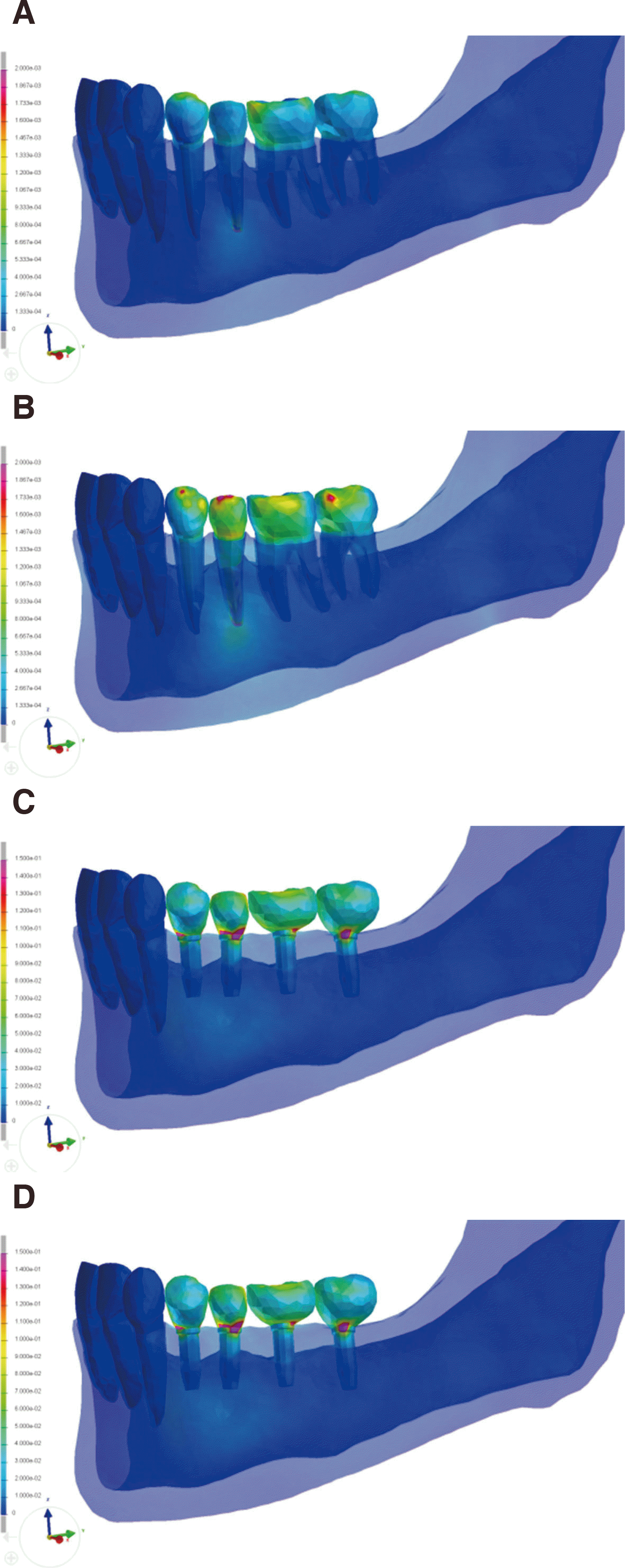
Table 1
Experimental models setup
Table 2
Material properties
Table 3
Maximum von Mises stress value (MPa) and location of each model
| Maximum von Mises stress | Location | |
|---|---|---|
| NA | 28.41 | 2nd premolar apex |
| NN | 51.57 | 2nd premolar apex |
| IA | 882.40 | 2nd premolar fixture screw |
| IN | 888.28 | 2nd premolar fixture screw |




 PDF
PDF Citation
Citation Print
Print



 XML Download
XML Download