This article has been
cited by other articles in ScienceCentral.
Abstract
Pain is subjective, while statistics related to pain research are objective. This review was written to help researchers involved in pain research make statistical decisions. The main issues are related with the level of scales that are often used in pain research, the choice of statistical methods between parametric or nonparametric statistics, and problems which arise from repeated measurements. In the field of pain research, parametric statistics used to be applied in an erroneous way. This is closely related with the scales of data and repeated measurements. The level of scales includes nominal, ordinal, interval, and ratio scales. The level of scales affects the choice of statistics between parametric or non-parametric methods. In the field of pain research, the most frequently used pain assessment scale is the ordinal scale, which would include the visual analogue scale (VAS). There used to be another view, however, which considered the VAS to be an interval or ratio scale, so that the usage of parametric statistics would be accepted practically in some cases. Repeated measurements of the same subjects always complicates statistics. It means that measurements inevitably have correlations between each other, and would preclude the application of one-way ANOVA in which independence between the measurements is necessary. Repeated measures of ANOVA (RMANOVA), however, would permit the comparison between the correlated measurements as long as the condition of sphericity assumption is satisfied. Conclusively, parametric statistical methods should be used only when the assumptions of parametric statistics, such as normality and sphericity, are established.
Go to :

Keywords: Analysis of variance, Biostatistics, Nonparametric, Normal distribution, Pain measurement, Visual analog scale
INTRODUCTION
Parametric statistics usually start from some kind of assumptions such as normal distribution of data, independence of data, identical variance and so on. The main reason that many researchers get in trouble with parametric statistics would be ignoring the process of confirming the assumptions which precedes the application of parametric statistics. The data which is frequently used in pain research have several characteristic features which potentially disturb the assumption of parametric statistics.
In the field of pain research, there are some particular aspects of statistics which are worth looking into. For the first particular aspects, it is the scale of data. To evaluate the degree of pain, a Likert-type scale, such as numerical rating scale (NRS) or visual analog scale (VAS), is frequently used. Those scales are generally categorized as ordinal scales which means that parametric statistics are not appropriate for those scales. Nevertheless, there have still been controversies as to whether the VAS should be treated as an ordinal scale or an interval scale. Furthermore, the issue on how to handle scales which are composed of several ordinal subcategories has still not ceased.
Another special aspect is the repeated measure of the intensity of pain during the research. Repeated measurements of the same subject must have a relationship between each other. Parametric statistics, such as ANOVA, generally assume the independence of the data, so that the ANOVA would not be applicable for comparison of repeated measured data in the same subject. To make the comparison possible in such cases, repeated measures of ANOVA (RMANOVA) suggests another alternative assumption, the so-called “sphericity assumption”, in which the correlations with each repeated measurements should be even.
In this review, several statistical issues which are related to pain research will be presented and some suggestions or recommendations will be described.
Go to :

MAIN BODY
1. Scales of measure
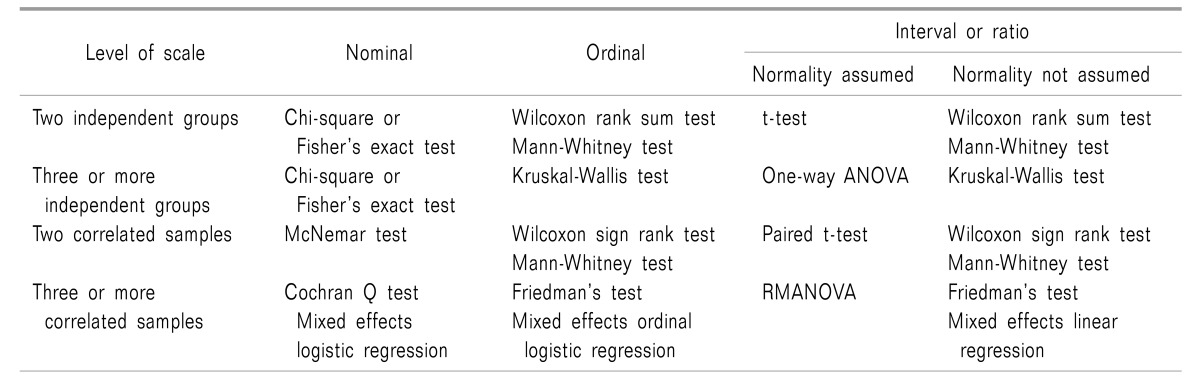
The important factors to be considered in determining the statistical method are the level of measurement of the data, the number of groups to be compared, and the independence of the data. The level of data measurements is also referred to as the scale of measure. The scales of measure include the nominal, ordinal, interval, and ratio scales (
Table 1). The reason for distinguishing these scales is that there is a difference in the amount of information according to the scale, subsequently, this difference influences the selection of the statistical method.
Table 1
Examples of Level Measurements


The information of scales includes arithmetic operability and the concept of zero and so on. When we compare the effect of treatments on back pain, if the treatment modalities included oral medication, exercise therapy, and a nerve block, these three methods of treatments can be called nominal scales. There is no zero point in the nominal scale. The information included is a simple name so that it is nonsenses to do arithmetic calculations between the names of the therapies.
If the measurement of pain intensity is scaled as no pain, mild pain, moderate pain, severe pain, and the worst pain imaginable, this type of scale is called an ordinal scale. It is possible to know the difference in the pain intensity between the markers in order, but it is not possible to know whether the interval of pain between the markers is same or not. It is not possible to do arithmetic calculation as well.
On the other hand, time interval and body temperature are examples of interval scales. The interval scale literally has constant intervals between the markers so that it is possible to do arithmetic calculation between the markers and to set an arbitrary zero. In the case of body temperature, 0℃ can be set as an arbitrary zero in a relative sense rather than as an absolute temperature.
The ratio scale contains the largest amount of information. It has a constant interval and absolute zero as well. It is possible to do arithmetic operations. Most of the measurements in the physical sciences are included. For example, length, weight, lap time, and the hematocrit, which is represented by a percentile, are classified as ratio scales.
2. Parametric statistics vs visual analogue scale (VAS)
The issues regarding the scale would matter not only with the amount of information contained in the scale itself but also with the distribution characteristics of the data. In the case of the nominal or ordinal scale, there appears to be a high probability of skewed distribution rather than the normal distribution. The scales which are used to measure pain intensity, however, are often misunderstood and inappropriately applied in statistics. Sometimes, parametric statistics would be applied even if the data are composed of ordinal or nominal scales. Yim et al. [
1] reported that the most frequent error in inferential statistics is that parametric statistics were applied inappropriately when non-parametric statistics should have been applied.
The distribution of data is another determinant factor in whether parametric statistics could be applied or not. For normally distributed data, parametric statistics can be applied. On the other hand, for nominal or ordinal scale data, it is a principle that non-parametric statistics should be applied. A general example of how a statistical method would be chosen is summarized in
Table 2 according to the scale, the number of groups, and the independence of the data.
Table 2
Examples of the Choice of Statistical Method

It is important to check the level of the scales of data which are often used for evaluating the pain itself or the performance impairments caused by the pain. The most commonly used measures of pain and performance impairments include the numeric rating scale (NRS), VAS, Wong-Baker face pain rating scale, McGill pain questionnaire, Karnofsky performance scoring, Oswestry disability index (ODI), and so on.
For the NRS, it is obvious that it is ordinal scale. It means that nonparametric statistics should be applied for the NRS scale. When it come to the VAS score, however, there is something to be discussed about the scale and statistical methods.
It has been the dominant view that the VAS score is ordinal scale. Recently, there have been many disagreements as to whether the data measured by the VAS should be considered as an ordinal scale or an interval or ratio scale. Regardless of the scale issues, it is not surprising that non-parametric statistical methods are usually used for the VAS scale because the data measured with it are usually not normally distributed. Nevertheless, one paper has argued that the ordinal scale can be used in parametric statistics [
2]. Other papers have shown that parametric statistics can be applied with an emphasis on the character of the VAS as an interval or ratio scale [
34]. Dexter and Chestnut [
5] reported that the t-test or ANOVA test can be applied to the VAS without inflation of the type 1 error. They appended, however, a requirement in which the extreme value of the VAS, 0 and 10, should be less than 16%, if not, accuracy cannot be guaranteed [
5].
3. Summation scale of ordinal subcategories
There are some particular types of scales, such as the ODI, which are taken from the sum of the scores of multiple ordinal scales. The ODI consists of ten questions which should be answered on an ordinal scale ranging from 0 to 5 so that the total possible score ranges from 0 to 50. Each of the questions which make up the ODI is definitively an ordinal scale. Nevertheless, it is still confusing whether the total score should be treated as an ordinal scale as well, or if it could be treated as an interval scale.
It is not easy to find a document that gives a definitive answer to this problem. Nunnally and Bernstein [
6] have found that if the number of categories in the subordinate scale is more than 7–11, the total score could be treated as an interval scale. Some statisticians have shown that applying parametric statistics to ordinal scales is acceptable. Heeren and D'Agostino [
7] have shown that a small number of sample data in a rank scale can be applied without increasing type 1 error, even if parametric test is used instead of a non-parametric test. Sullivan and D'Agostino [
8] also claimed that ANOVA and type 1 error inflation did not occur in the analysis of rank-order data.
Even though there have been some reports which support treating the total score of the ODI as an interval scale [
6], it is still unlikely that the scale of total scores has even intervals between the scores to scores due to the different difficulty levels of each questionnaire category. Although some statisticians showed that there was no increase of the type 1 error even when the ordinal scales are applied to parametric statistics, this is not widely accepted and still considered inappropriate from a theoretical point of view.
Using the nonparametric statistical method is recommended if the data originated from an ordinal scale. When it comes to the VAS, as long as the normality assumption is guaranteed, it is generally accepted that parametric statistical methods may be applied. For scales which are composed of many subcategories of ordinal scales, use of parametric statistical methods has not been fully accepted yet. Nevertheless, if researchers insist on using parametric statistical methods for ordinal scale data, passing the statistical reviews which they should encounter during submission cannot be guaranteed, even though the aforementioned references could support their use of parametric statistical methods.
4. Problems of repeated measurements
Another particular feature of data which is related to pain research is repeated measurements. Most pain assessments are not completed with only one measurements of the pain. The measurement would be often repeated according to a time schedule with a single subject. That is, after administration of pain medication or nerve blocks, the effects are evaluated using pain assessments three or four times at predetermined time intervals.
To know whether the pain medicine is effective or not, the pain scores before and after administration should be compared. The data which are measured repeatedly in one individual create another complex statistical problem, which means that they are not independent of each other. When the pain scores are assessed twice, before and after a procedure, the two data are not independent of each other. In this case the paired t-test would be a candidate for the statistical method rather than the student's t-test which should be used for independent measurements.
How about when the pain assessments are repeated three times or more? Have you heard about paired-ANOVA? There is actually nothing like that. For example, when the heights of students in a school are compared between the 1st, 2nd, and 3rd grades, ANOVA analysis will be an appropriate statistical method since the heights of each grade are measured independently. If the point of interest is the growth of the students as they advance from 1st to 3rd grades, the heights should be measured three times as they grow up from grades 1 to 3. In this case, the height measurements which come from the same individuals at each grades are not independent from each other and the measurements must be correlated with each other. In this case, it looks like ANOVA is no longer available.
Statisticians, however, suggests another way which makes it possible to apply ANOVA even if the data are from repeated measurements. They boldly gave up the independences of the data between the repeated measurements since the data would never be independent by any means. Instead, they require evenly distributed correlations between the repeated measurements. That is, if you want to compare the heights of persons who are standing on a staircase as shown in the
Fig. 1, it is difficult to compare the height due to the presence of the stairs. But once the height of stairs is determined to be even, you could compare the heights quite easily. The stairs represent the correlations between repeated data which makes it difficult to compare independently. Getting the stair height even represents making the correlations between the measurements even. After all, whenever the correlations between repeated measurements are evenly distributed, the ANOVA could be applied. The only thing that one should back up is the evidence of the even distribution of the correlations. Then, how to back it up?
 | Fig. 1Comparison of the heights between the children who stand on different level of stairs is difficult. The stairs would stand for the relationship between repeated measurements in RMANOVA, which could make it difficult to compare the height directly (A). Once the level of stairs gets even, it would make it easier to compare the heights (B).
|
5. Sphericity assumption
The relationships between repeatedly measured data could be evaluated by a correlation coefficient. To show whether these correlation coefficients are equal to each other or not, a 3 by 3 table can be created as shown in the
Fig. 2. The correlation coefficient of the diagonal direction is 1, since those correlate to themselves. If ρ which is the correlation coefficient off the diagonal line is constant for all, statisticians often refer to these evenly distributed correlations as ‘the sphericity assumption being satisfied’. To confirm the sphericity assumption, a sphericity test such as Maucley's test should be done. As long as the sphericity assumption is satisfied, the ANOVA can be applied for the repeatedly measured data, and the result of ANOVA can be accepted.
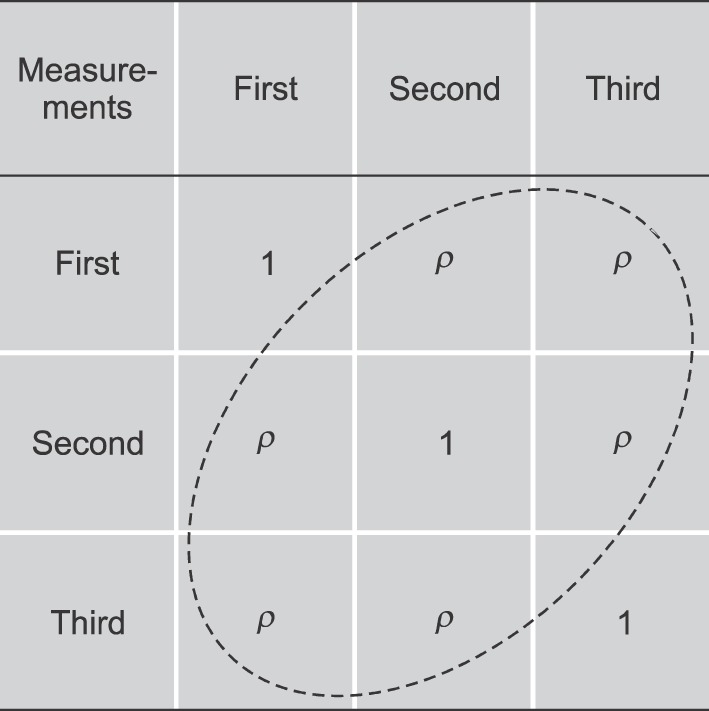 | Fig. 2The correlation coefficients between repeated measurements are presented in a manner of table. The coefficient of diagonal parts should be 1 due to correlation by itself. If the coefficients of off-diagonal parts are same for all, it can be announced that the sphericity assumption is satisfied. Maucley's sphericity test is one of the frequently used sphericity assumption tests.
|
In the end, these series of processes are well known and is called the repeated measures of ANOVA (RMANOVA). It means that the RMANOVA is not a brand new statistic, it is just ANOVA based on an additional assumption in which the variance differences between repeated measurements are equal over the whole. Therefore, it is important to confirm the sphericity assumption in performing RMANOVA [
9].
6. Comparing between subject factors
In cases of RMANOVA analysis in pain research, one of the most frequently encountered research designs has one between-subjects factor and one within-subjects factor. The between-subjects factor indicates the type of treatments or drugs, and the within-subjects factor means the changes in pain over time (
Fig. 3). For the between-subjects factor, one can divide groups according to the type of treatment or medication. For the within-subjects factor, differences between the series of time interval within a group or overall groups would be a point of interest.
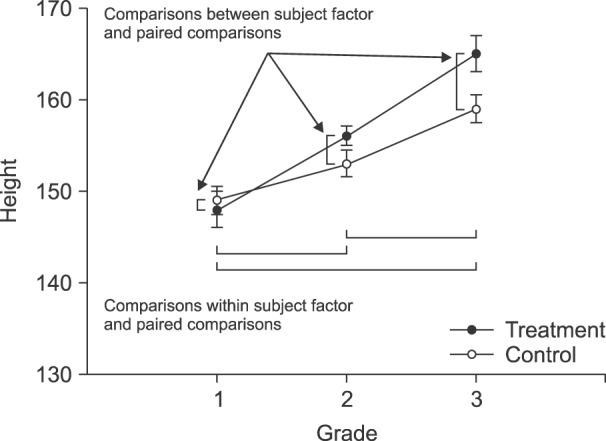 | Fig. 3To know the differences of height within subject as students grow up, RMANOVA is available and the sphericity assumption should be guaranteed. To compare within subject factor which means the differences between each grades, paired comparisons between the grades could be done with adjustment of significance level like the Bonferroni's correction. To compare the between subject factor at each grade, paired comparisons could be done with significance levels adjusted by like the Bonferroni's procedure.
|
In practical statistics, frequently encountered problems which is related with such study design would be a number of repeated measurements. To investigate the differences between the time points, paired comparisons are needed between the series of times to find out which time point scores are different from which other time points. In the process of repeated paired comparisons, the problem of the inflation of type I error would become a matter of concern [
10]. This problem is not limited to the paired comparison between the time series. It also matters when one makes a comparison between group effects. The researchers are mainly interested in the differences between groups on specific time point rather than the overall differences between groups. For such a reason, comparisons between groups used to be done at all repeated time points. The more often the comparisons are repeated, the more type I error would be inflated.
To solve the inflation of type I error, an adjustment of significance level would be recommended in a manner like the Bonferroni's correction [
11]. For Bonferroni's correction, the total significance level is divided with the number of comparisons and the hypothesis test of each comparison is determined with the divided significance level. Even though the Bonferroni adjustment is proposed as a method to prevent the inflation of Type I errors, ironically it would cause another problem. If there are a lot of comparisons, the adjusted level of significance becomes so small that most of the null hypothesis would have a chance to be accepted and the Type II error turns out to be increased [
1112]. There have been several ways of adjusting the significance level in order to solve these type I or II error problems [
1314], but they do not look like definitive answers.
In the field of pain research, the problems which are caused by the adjustment of significance level could be avoided with a simpler study design which trims out unnecessary repeated measurements. It is important to determine the appropriate number of repeated measurements which are deemed necessary from the beginning of studies, and an effort should be made to make the repetitions as few as possible. However, there seem to be no references about the appropriate number of repetition.
In summary, description of the sphericity test should always be accompanied with the RMANOVA in statistical method sections. Adjustment of significance level cannot be ignored in a repeated measure study design, and the methods of adjustment like the Bonferroni adjustment should be also described in the statistical method.
Go to :

CONCLUSIONS
Most of the scales which are used in the field of pain research would be ordinal or nominal scales. The VAS is generally accepted as an interval or ratio scale, so that parametric statistics could be applicable to it only if the data shows normal distribution. But, there are still controversies about that.
Researchers should be aware that all the parametric statistics start from some kinds of assumptions about data such as independence, identical variance, and normal distribution. If these assumptions are not guaranteed, it would be better to choose nonparametric statistical methods. The repeated measurements necessarily add complexities of data such as correlations between measurements. Before applying the RMANOVA, the sphericity assumption which guarantees the even distribution of correlations between repeated measurements should be tested. For post hoc analysis, contrast which means paired comparisons can be applied after RMANOVA, in such case, adjustment of significance level, such as Bonferroni adjustment, should be included.
Go to :

ACKNOWLEDGEMENTS
This work was supported by a 2-Year Research Grant of Pusan National University.
Go to :

References
1. Yim KH, Nahm FS, Han KA, Park SY. Analysis of statistical methods and errors in the articles published in the Korean Journal of Pain. Korean J Pain. 2010; 23:35–41. PMID:
20552071.

2. Norman G. Likert scales, levels of measurement and the “laws” of statistics. Adv Health Sci Educ Theory Pract. 2010; 15:625–632. PMID:
20146096.

3. Huskisson EC. Measurement of pain. J Rheumatol. 1982; 9:768–769. PMID:
6184474.

4. Price DD, McGrath PA, Rafii A, Buckingham B. The validation of visual analogue scales as ratio scale measures for chronic and experimental pain. Pain. 1983; 17:45–56. PMID:
6226917.

5. Dexter F, Chestnut DH. Analysis of statistical tests to compare visual analog scale measurements among groups. Anesthesiology. 1995; 82:896–902. PMID:
7717561.

6. Nunnally JC, Bernstein IH. Psychometric theory. 3rd ed. New York (NY): McGraw-Hill Book Company;1994. p. 115.
7. Heeren T, D'Agostino R. Robustness of the two independent samples t-test when applied to ordinal scaled data. Stat Med. 1987; 6:79–90. PMID:
3576020.

8. Sullivan LM, D'Agostino RB Sr. Robustness and power of analysis of covariance applied to ordinal scaled data as arising in randomized controlled trials. Stat Med. 2003; 22:1317–1334. PMID:
12687657.

9. Lee Y. What repeated measures analysis of variances really tells us. Korean J Anesthesiol. 2015; 68:340–345. PMID:
26257845.

10. Kim TK. Understanding one-way ANOVA using conceptual figures. Korean J Anesthesiol. 2017; 70:22–26. PMID:
28184262.

11. Bland JM, Altman DG. Multiple significance tests: the Bonferroni method. BMJ. 1995; 310:170. PMID:
7833759.
12. Rothman KJ. No adjustments are needed for multiple comparisons. Epidemiology. 1990; 1:43–46. PMID:
2081237.

13. Perneger TV. What's wrong with Bonferroni adjustments. BMJ. 1998; 316:1236–1238. PMID:
9553006.

14. Glickman ME, Rao SR, Schultz MR. False discovery rate control is a recommended alternative to Bonferroni-type adjustments in health studies. J Clin Epidemiol. 2014; 67:850–857. PMID:
24831050.

Go to :








 PDF
PDF Citation
Citation Print
Print




 XML Download
XML Download