Texture, Morphology, and Statistical Analysis to Differentiate Primary Brain Tumors on Two-Dimensional Magnetic Resonance Imaging Scans Using Artificial Intelligence Techniques

Subrata Bhattacharjee; Deekshitha Prakash; Cho-Hee Kim; Hee-Cheol Kim; Heung-Kook Choi

doi:10.4258/hir.2022.28.1.46

Journal List > Healthc Inform Res > v.28(1) > 1158772

Go to TopGo to Top Go to BottomGo to Bottom

TOOLS

Bhattacharjee, Prakash, Kim, Kim, and Choi: Texture, Morphology, and Statistical Analysis to Differentiate Primary Brain Tumors on Two-Dimensional Magnetic Resonance Imaging Scans Using Artificial Intelligence Techniques

Original Article

Healthcare Informatics Research 2022; 28(1): 46-57.

Published online: 31 January 2022

DOI: https://doi.org/10.4258/hir.2022.28.1.46

Texture, Morphology, and Statistical Analysis to Differentiate Primary Brain Tumors on Two-Dimensional Magnetic Resonance Imaging Scans Using Artificial Intelligence Techniques

Subrata Bhattacharjee¹

, Deekshitha Prakash¹

, Cho-Hee Kim²

, Hee-Cheol Kim²

, Heung-Kook Choi^1,³

¹Department of Computer Engineering, u-AHRC, Inje University, Gimhae, Korea

²Department of Digital Anti-Aging Healthcare, Inje University, Gimhae, Korea

³AI R&D Center, JLK Inc., Seoul, Korea

Corresponding Author: Heung-Kook Choi, Department of Computer Engineering, u-AHRC, Inje University, 197, Inje-ro, Gimhae 50843, Korea. Tel: +82-55-320-3643, E-mail: cschk@inje.ac.kr (https://orcid.org/0000-0002-1372-7052)

Received 15 October 2020 Revised 6 October 2021 Revised 21 December 2021 Accepted 5 January 2022

(open-access, http://creativecommons.org/licenses/by/4.0):

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

Objectives

A primary brain tumor starts to grow from brain cells, and it occurs as a result of errors in the DNA of normal cells. Therefore, this study was carried out to analyze the two-dimensional (2D) texture, morphology, and statistical features of brain tumors and to perform a classification using artificial intelligence (AI) techniques.

Methods

AI techniques can help radiologists to diagnose primary brain tumors without using any invasive measurement techniques. In this paper, we focused on deep learning (DL) and machine learning (ML) techniques for texture, morphological, and statistical feature classification of three tumor types (namely, glioma, meningioma, and pituitary). T1-weighted magnetic resonance imaging (MRI) 2D scans were used for analysis and classification (multiclass and binary). A total of 102 features were calculated for each tumor, and the 20 most significant features were selected using the three-step feature selection method, which included removing duplicate features, Pearson correlations, and recursive feature elimination.

Results

From the predicted results of multiclass and binary classification, a long short-term memory binary classification (glioma vs. meningioma) showed the best performance, with an average accuracy, recall, precision, F1-score, and kappa coefficient of 97.7%, 97.2%, 97.5%, 97.0%, and 94.7%, respectively.

Conclusions

The early diagnosis of primary brain tumors is very important because it can be the key to effective treatment. Therefore, this research presents a method for early diagnoses by effectively classifying three types of primary brain tumors.

Keywords: Brain Tumor, Magnetic Resonance Imaging, Deep Learning, Machine Learning, Classification

I. Introduction

Brain tumors cause a substantial number of deaths globally. Generally, a brain tumor is made up of cells in the brain like all other organs. Brain tumors are groups of cells in the brain, which could be non-cancerous, pre-carcinoma, or malignant [1]. When cancerous or non-cancerous tumors grow, they can cause elevated pressure inside the skull [2]. Therefore, these tumors can be life-threatening and can cause brain damage. Generally, the diagnosis of brain tumors begins with magnetic resonance imaging (MRI). Other modalities for analyzing brain tumors include X-rays, computed tomography (CT) scans, and positron emission tomography (PET) scans. However, MRI is more useful than other modalities because it provides detailed information about the tumor type, size and shape, position, anatomy, and vascular supply. Therefore, MRI is a suitable choice to study brain tumors. Brain tumors can be categorized as primary (originates in the brain), and secondary (occurs in the brain when cancer cells spread from other organs, such as the lungs, kidney, or breast) [3]. Some of the common primary tumors that grow gradually are meningioma, glioma, and pituitary tumors. Meningiomas occur in the meninges (membranes that enclose the brain and spinal cord), and are more common in women than men, gliomas develop from glial cells, and pituitary tumors grow on the area of the pituitary gland [4]. These types of tumors can be cancerous or non-cancerous. The World Health Organization classification splits meningiomas into three different grades: benign meningioma (grade 1), atypical meningioma (grade 2), and malignant meningioma (grade 3) [5].

Analyzing the progression of brain tumors based on texture, morphological, and statistical feature classification is a highly challenging task. These features are called radiomic features and can be extracted using the data-characterization algorithms from different types of radiological images, such as MRI, CT, X-rays, ultrasound, and PET. Radiomics [6] has emerged as a promising non-invasive method in recent years, and radiomic features enable quantitative measurements of parameters such as shape or heterogeneity. Many radiologists use the traditional approach for classifying brain tumors in MRI scans, although it is quite difficult to make 100% correct predictions based on tumor texture and shape. Artificial intelligence (AI)-based classification using deep learning (DL) and machine learning (ML) algorithms [7] is popular in the field of medical and biological image analysis, as a method that provides radiologists with a second opinion.

The aim of this paper was to differentiate the tumor types (meningioma, glioma, and pituitary) by performing binary and multiclass classification using AI techniques. In this study, we developed a long short-term memory (LSTM) [8] neural network model and used ML classifiers, namely support vector machine (SVM), k-nearest neighbor (KNN), logistic regression (LR), random forest (RF), and linear discriminant analysis (LDA), to perform multiclass and binary classification. In general, LSTM is used and well suited in classifying and making predictions based on convolutional neural network (CNN)-extracted features [7] or time-series data. However, the LSTM model was used in our research to classify handcrafted (texture, morphological, and statistical) features. Feature reduction is another important step to save computation time, perform AI-based classification, and achieve better accuracy. In the present work, we used feature duplication, Pearson correlation coefficients, and recursive feature elimination (RFE) to reduce the number of features from the dataset and select the most significant features. Each classification model’s performance was evaluated using accuracy, precision, recall, the F1-score, the kappa coefficient, and the receiver operating characteristic (ROC) curve. Moreover, a comparative analysis was performed between learning algorithms for multiclass and binary classification tasks, as well as a comparison between related research and our method.

The rest of this paper is organized as follows. A detailed description of the dataset, tumor extraction method, feature extraction and selection, and DL and ML classification is presented in Section II. The performance of the learning algorithms for binary and multiclass classification is reported in Section III. Finally, the results are discussed and the paper is concluded in Section IV.

II. Methods

1. Dataset Information

The MRI image dataset [9] was collected online and it is publicly available. Originally, the data samples were acquired from 233 patients at Nanfang Hospital and Tianjin Medical University General Hospital in China. The brain T1-weighted contrast-enhanced MRI (CE-MRI) dataset was first used by Cheng et al. [10], who uploaded the dataset on the above website. The MRI slices used for this study are two-dimensional (2D), and the resolution of each image slice is 512 × 512 with a pixel size of 0.49 × 0.49 mm². The thickness and gap of each slice are 6 mm and 1 mm, respectively. The dataset contains a total of 3,064 T1-weighted MRI and annotated mask images with three different planes, namely axial (1,025 slices), coronal (1,045 slices), and sagittal (994 slices). The brain tumor dataset includes three classes: glioma, meningioma, and pituitary. Figure 1 shows example images of the brain tumors and annotated masks in three different views.

2. Research Methodology

To perform the analysis, classification, and prediction, we first input all the brain tumor samples with their respective mask images. Each brain tumor region-of-interest (ROI) was extracted by overlapping the image mask on the original samples of gliomas, meningiomas, and pituitary tumors. Feature extraction was then performed from each ROI using PyRadiomics [11], which is an open-source Python package for feature extraction from medical images. Next, three-step feature selection was performed by leveraging the filter methods (removing duplicate features and Pearson correlation coefficients) and the wrapper method (RFE). Finally, AI-based multiclass and binary classification using LSTM, SVM, KNN, LR, RF, and LDA was performed to predict the classes (glioma, meningioma, and pituitary) of brain tumors. In this paper, we used DL and ML techniques to classify the handcrafted features extracted from the ROIs of brain tumors of three different classes. Figure 2 shows the research pipeline for tumor extraction, features calculation and selection, model implementation, and classification, respectively.

3. Tumor Extraction

Tumor extraction can be treated as a pattern recognition technique as it requires the classification of pixels. To detect tumor tissues on medical imaging, extraction is necessary. Extraction separates the brain tumor region from MRI scans into two regions. One of the regions contains tumor cells in the brain, while the other contains normal brain cells. This process is quite challenging, as the classification task completely depends on the extracted tumor. The extraction of brain tumors from MRI scans is an essential requirement for clinical diagnosis since manual extraction is fatiguing and time-consuming. Tumor extraction from T1-weighted 2D MRI slices (axial, coronal, and sagittal) is quite difficult without using an annotation mask image. In this study, we extracted the ROI of brain tumors by overlapping the annotated binary mask on the original image. We obtained the mask images along with the dataset that was created by the radiologists. Figure 3 shows the extracted MRI patches that were used to compute the radiomic features [12] for the classification.

4. Feature Computation and Selection

Feature extraction is a prominent method in pattern recognition and image processing for the analysis of patterns in an image [13]. PyRadiomics (version 2.2.0), an open-source Python package, was used to extract a large number of radiomic features based on heterogeneity (i.e., image gray levels) and shape (i.e., the segmented region in an image).

In this paper, textural, morphological, and statistical features were computed from the area of brain tumors on 2D MRI scans using seven different techniques: first-order statistics (FOS), 2D shape-based analysis, gray level co-occurrence matrix (GLCM), gray level run length matrix (GLRLM), gray level size zone matrix (GLSZM), gray level dependence matrix (GLDM), and neighboring gray-tone difference matrix (NGTDM) [14]. In total, 102 2D features were initially extracted from the regions of each tumor. Out of these, 18 were FOS, 9 were 2D shape-based, 24 were GLCM, 16 were GLRLM, 16 were GLSZM, 14 were GLDM, and 5 were NGTDM.

Feature selection is an important step before DL and ML classification. Many feature selection methods have been proposed in the past decades. In general, methods for feature selection can be categorized into three groups: filter methods, wrapper methods, and embedded methods [15]. In filter methods, the relevance of the features is selected based on univariate statistics rather than cross-validation (CV) performance. Some common filter methods are information gain, the chi-square test, the Fisher score, Pearson correlation coefficients, and the variance threshold [16]. In contrast, wrapper methods consider the effectiveness of the features based on the performance of the classifiers. Some common wrapper methods are RFE, sequential feature selection algorithms, and genetic algorithms [17]. Embedded methods work similarly to wrapper methods, and two common methods are L1 (LASSO) regularization and decision trees.

To perform the process of feature reduction, we used three different techniques: feature de-duplication, Pearson correlation coefficients, and RFE.

First, duplicate features were removed by searching for similar values in the columns of the dataset. Another reason for removing them is that they do not lead to any changes to the training algorithm; instead they add unnecessary delays to the training time. Second, Pearson correlation coefficients were used to remove highly correlated features (with a correlation more than 85%) from the dataset. Finally, RFE was used to eliminate the features that were weakest and worst-performing. Among all the extracted features, 101 were selected in the first step, 56 were selected in the second step, and 20 were selected in the third step, as shown in Figure 4. Table 1 shows the final selected radiomic features used for the classification, arranged according to the RFE ranking, along with their equations.

5. Tumor Classification

Tumor classification was executed using the selected features that were extracted from the ROIs of T1-weighted MRI scans. The main aim of our study is the development of LSTM [18] and ML models for the classification of the textural, morphological, and statistical features into three classes of brain tumor, namely glioma, meningioma, and pituitary. Therefore, to develop the DL- and ML-based model, six different algorithms (LSTM, SVM, KNN, LR, RF, and LDA) were used for classification.

There are two types of LSTM architecture: unidirectional and bidirectional. In this study, we used a bidirectional LSTM (BiLSTM) model to perform classification using the selected features. The main difference between the two architectures is that in unidirectional LSTM, only past information is preserved because it can read the inputs only from the past. Instead, in BiLSTM, the inputs are learned in two ways: first, with input from the past to the future, and second, with input from the future to the past. Therefore, BiLSTM models [19] perform better than unidirectional LSTM as they preserve information from both past and future and can understand the context better. In LSTM, the cell memory is controlled through three different gates that regulate the information flow: namely, input, forget, and output. Supplementary Figure S1 shows a representation of the LSTM model. To perform LSTM classification, a customized activation function was used instead of the rectified linear unit (ReLU). The idea of implementing a customized function was taken from Google Brain [20], and the function was named “Swish,” which tends to work better than ReLU. Supplementary Figure S2 shows the graph plots for ReLU and customized activation functions. The equations used to compute these functions can be expressed as:

(1)

\begin{matrix} R e L U = max (0, x) \\ f (x) = {\frac{0 f o r x < 0}{x f o r x = > 0} \end{matrix}

(2)

\begin{matrix} C u s t o m i z e d f (x) = x \times σ (β \times x) \\ σ = \frac{1}{1 + e^{- β x}} \end{matrix}

where x is the input to the network, β is the beta value for changing the variation of the curve, and σ is a sigmoid function.

ML models are essential for the classification of hand-crafted features, and the model’s hyperparameters control the fluctuation of the accuracy. Not every ML algorithm was used for both binary and multiclass classification [21]; LR was used for binary classification, LDA was used for multiclass classification, and the other three algorithms (SVM, KNN, RF) [22] were used for both binary and multiclass classification. The main purpose of implementing six algorithms for feature classification was to analyze and compare the output results between the classifiers.

To classify the classes of brain tumors using AI techniques (LSTM and ML), we divided the dataset into two folds—training (90%) and testing (10%)—for sequence classification, as shown in Table 2. Furthermore, to carry out sequence data classification using LSTM, the training dataset was further divided, such that 80% and 20% of data were assigned for training and validation, respectively. Hyperparameter tuning is important for both LSTM and ML modules, and the information and specifications regarding all the algorithms used for the development are shown in Supplementary Table S1. For ML classification, the training dataset was not divided into two splits like LSTM instead, we used five-fold cross-validation to check the generalization capability of the classifiers.

To evaluate the performance of the classification models, we used six different performance metrics [23]: accuracy, recall, precision, the F1-score, and the kappa coefficient. The equations used to compute these metrics are as follows:

(3)

A c c u r a c y = \frac{T P + T N}{T P + T N + F P + F N}

(4)

R e c a l l = \frac{T P}{T P + T N}

(5)

P r e c i s i o n = \frac{T P}{T P + F P}

(6)

F 1_{s c o r e} = 2 \times \frac{P r e c i s i o n \times R e c a l l}{P r e c i s i o n + R e c a l l}

(7)

K a p p a C o e f f i c i e n t = \frac{N Σ_{i = 1}^{n} m_{i, i} - Σ_{i = 1}^{n} (G_{i} C_{i})}{N^{2} - Σ_{i = 1}^{n} (G_{i} C_{i})}

where TP, TN, FP, and FN indicate true positives, true negatives, false positives, and false negatives, respectively. In Eq. (5)i is the number of classes, N is the sum of classified values compared to true values, m_i_,_i is the number of true class (i) values, which is also classified as i (i.e., diagonal values of confusion matrix), C_i is the sum of predicted values (i), and G_i is the sum of the true values (i). Accuracy is the closeness of the measurements to a specific value, recall is the measurement of the total amount of relevant occurrences that were truly predicted, and precision is the closeness of the measurements of relevant occurrences among the predicted instances. The F1-score, which is a better measure than accuracy, is computed from the recall and precision of the test. The kappa coefficient is a measure of agreement that is used to assess the quality of the classification.

III. Results

The classification performance was evaluated using the different performance metrics discussed in the previous section. In total, 3,064 MRI scans were used to carry out the analysis. The scans were obtained from 233 patients who had primary brain tumors (glioma, meningioma, and pituitary). The MRI scans were divided into training and testing data sets at a 9:1 ratio. The brain tumors from 2D MRI scans were extracted with the help of the ground truth/mask images using MATLAB R2020b (MathWorks, Natick, MA, USA), and AI classification was performed using Anaconda (a Jupyter notebook).

The learning algorithms that were used for binary and multiclass classification showed effective results for classifying three different classes of brain tumors. Table 3 shows the overall results for LSTM and the ML classification, and a comparative analysis between the six different algorithms used for classifying the textural, morphological, and statistical features. The output results of the classification that are shown in Table 4 are based on the test set. Both LSTM and ML models were trained and tested with the same dataset. Figure 5 shows the ROC curve and corresponding area under the curve (AUC) that depicts the comparison results for each classifier.

Due to the similar feature values of pituitary and meningioma tumors, the classifiers could not distinguish them accurately. As a result, the performance of the multiclass (glioma vs. meningioma vs. pituitary) and binary (meningioma vs. pituitary) classifications was not satisfactory. However, the first and second binary classifications (glioma vs. meningioma and glioma vs. pituitary) performed well compared to other groups. Supplementary Figures S3 and S4 depict the scatter pair plot of a few data samples used for multiclass and binary classification, respectively. The distribution of data samples was plotted to analyze visually the relationship between the variables.

IV. Discussion

The brain tumor was extracted using the mask image of the tumor by overlapping the original image. We did not focus on automatic segmentation because this paper aimed to extract multiple types of features and develop DL and ML algorithms for classification. To carry out the ML classification, five-fold CV was applied for validating and analyzing the performance of the model. Meanwhile, for LSTM classification, 20% of the data was separated from the training set for validation. Generally, five-fold CV is used in applied ML to estimate the skill of the models. In DL, we normally avoid CV because of the cost and time associated with training different models. Although the training approach is different in DL and ML classification, the model testing was carried out using the same test data (Table 2).

As seen in Table 3, binary classification achieved overall better results than multiclass classification. In classification using multiclass features, the error of one class can affect the results of other classes because the classification is not performed separately and independently. Instead, classification using binary features is performed separately and independently, and the impact of misclassification is not like that in multiclass classification. Out of four different classifications (multiclass and binary), the second classification (glioma vs. meningioma) showed promising and effective results. LSTM also outperformed all the ML classifiers by giving an overall accuracy, recall, precision, F1-score, and kappa coefficient of 97.7%, 97.2%, 97.5%, 97.0%, and 94.7%, respectively, for classifying glioma versus meningioma. Among all the ML classifiers, LR and LDA were used for binary and multiclass classification, respectively.

Moreover, we also analyzed the results and computation costs of each classifier, before and after feature selection. As discussed earlier in the Methods section, feature selection is very important for AI classification, and we perform feature selection not only to increase the accuracy of the models but also to reduce the computation time. We identified a slight improvement in classification performance (i.e., computation time) using the final selected features. Supplementary Figure S5 shows the correlation heatmap before and after feature selection, and Table 4 shows a comparison of the computational costs of each classifier based on all the features and selected features.

Similar research carried out a single multiclass classification using the T1-weighted CE-MRI dataset. Among these, none performed binary classification, which is also important for tumor diagnosis. However, in the present study, both binary and multiclass classification was performed using DL and ML techniques. Moreover, the best results obtained using the DL and ML techniques were compared with the results of similar studies, which are summarized and compared in Table 5.

• Cheng et al. [10] developed content-based image retrieval techniques for retrieving brain tumors from contrast-enhanced MRI scans. A novel feature extraction method was also proposed to improve the performance of tumor retrieval. The researchers applied adaptive spatial pooling and Fisher vector representation to local features from the raw images and subregions of the raw images, respectively.

• Sultan et al. [21], proposed DL-based CNN to classify different brain tumor types using two publicly available datasets. Dataset 1 classified tumors into meningioma, glioma, and pituitary tumors, and Dataset 2 differentiated between three glioma grades (grade II, grade III, and grade IV). Significant performance was achieved, with the best overall accuracy of 96.13% and 98.7% for Datasets 1 and 2, respectively.

• Alqudah et al. [24] used a CNN model to classify 3,064 T1-weighted MRI scans for grading brain tumors into three classes (glioma, meningioma, and pituitary). Their proposed CNN model performed well and achieved an accuracy of 98.9%, 99.0%, and 97.6% for the cropped, uncropped, and segmented lesions, respectively.

• Pashaei et al. [25] developed a CNN model with a kernel extreme learning machine classifier to classify brain tumors into meningioma, glioma, and pituitary tumors. They also compared their results according to the use of different classifiers such SVM, multilayer perceptron, stacking, extreme gradient boosting, radial basis function, KNN, and a deep neural network. Their proposed architecture achieved an overall accuracy of 93.68%.

• Diaz-Pernas et al. [26] presented a model using a deep CNN that included a multiscale approach for brain tumor segmentation and classification. For classification, their proposed neural model can analyze MRI images containing meningioma, glioma, and pituitary tumors. Their method performed well and obtained a remarkable tumor classification accuracy of 97.3%.

• Swati et al. [27] used a pre-trained deep CNN model and proposed a block-wise fine-tuning strategy based on transfer learning. A T1-weighted CE-MRI benchmark dataset was used to evaluate the proposed method. Their proposed architecture achieved an overall accuracy of 94.82% under five-fold CV.

• Ismael and Abdel-Qader [28] presented a framework for the classification of brain tumors in MRI images that combined statistical features and neural network algorithms. Feature selection was performed using a combination of the 2D discrete wavelet transform and 2D Gabor filter techniques. To perform classification, a back-propagation neural network classifier was selected to test the impact of classification. They also used a similar dataset consisting of 3,064 slices of T1-weighted MRI images with three types of brain tumors (meningioma, glioma, and pituitary). They achieved an overall accuracy of 91.9%.

• Badza and Barjaktarovic [29] presented a new CNN architecture for the classification of three brain tumor types. Their developed network was tested on T1-weighted CEMRI. The model performance was evaluated using four different approaches: combinations of two 10-fold CV methods and two databases. The network’s generalization capability was tested with one of the 10-fold methods (subject-wise CV), and the improvement was tested by using an augmented image database. They achieved an overall accuracy of 96.56% for the record-wise CV for the augmented data set.

• Cheng et al. [30] proposed a content-based image retrieval system for MRI images using the Fisher kernel framework. Their proposed method obtained a tumor classification accuracy of 94.7%.

In conclusion, this study presented results that may facilitate early diagnoses of brain tumors by effectively classifying three types of tumors. For a binary classification of glioma versus meningioma, the best results were obtained, with an average accuracy of 97.7% using an LSTM model.

Notes

Conflict of Interest

No potential conflict of interest relevant to this article was reported.

Acknowledgments

This research work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean government (MIST) (No. 2021R1A2C2008576).

Supplementary Materials

Supplementary materials can be found via https://doi.org/10.4258/hir.2022.28.1.46.

hir-2022-28-1-46-suppl.pdf

References

1. Herholz K, Langen KJ, Schiepers C, Mountz JM. Brain tumors. Semin Nucl Med. 2012; 42(6):356–70.

2. Kheirollahi M, Dashti S, Khalaj Z, Nazemroaia F, Mahzouni P. Brain tumors: special characters for research and banking. Adv Biomed Res. 2015; 4:4.

3. Lapointe S, Perry A, Butowski NA. Primary brain tumours in adults. Lancet. 2018; 392(10145):432–46.

4. Tunthanathip T, Kanjanapradit K, Ratanalert S, Phuenpathom N, Oearsakul T, Kaewborisutsakul A. Multiple, primary brain tumors with diverse origins and different localizations: case series and review of the literature. J Neurosci Rural Pract. 2018; 9(4):593–607.

5. Louis DN, Perry A, Reifenberger G, von Deimling A, Figarella-Branger D, Cavenee WK, et al. The 2016 World Health Organization Classification of Tumors of the Central Nervous System: a summary. Acta Neuropathol. 2016; 131(6):803–20.

6. Escudero Sanchez L, Rundo L, Gill AB, Hoare M, Mendes Serrao E, Sala E. Robustness of radiomic features in CT images with different slice thickness, comparing liver tumour and muscle. Sci Rep. 2021; 11(1):8262.

7. Babu PR, Babu IR. ML and DL based classification model of lung cancer using nodule volume. In : Proceedings of 2020 4th International Conference on I-SMAC (IoT in Social, Mobile, Analytics and Cloud); 2020 Oct 7–9; Palladam, India. p. 1001–6.

8. Kim CH, Bhattacharjee S, Prakash D, Kang S, Cho NH, Kim HC, et al. Artificial intelligence techniques for prostate cancer detection through dual-channel tissue feature engineering. Cancers (Basel). 2021; 13(7):1524.

9. Cheng J. Brain tumor dataset [Internet]. London, UK: Figshare;2017. [cited at 2022 Jan 20]. Available from: https://figshare.com/articles/dataset/brain_tumor_data-set/1512427/5 .

10. Cheng J, Huang W, Cao S, Yang R, Yang W, Yun Z, et al. Enhanced performance of brain tumor classification via tumor region augmentation and partition. PLoS One. 2015; 10(10):e0140381.

11. Duron L, Balvay D, Vande Perre S, Bouchouicha A, Savatovsky J, Sadik JC, et al. Gray-level discretization impacts reproducible MRI radiomics texture features. PLoS One. 2019; 14(3):e0213459.

12. Chen CH, Chang CK, Tu CY, Liao WC, Wu BR, Chou KT, et al. Radiomic features analysis in computed tomography images of lung nodule classification. PLoS One. 2018; 13(2):e0192002.

13. Chaddad A. Automated feature extraction in brain tumor by magnetic resonance imaging using Gaussian mixture models. Int J Biomed Imaging. 2015; 2015:868031.

14. Thibault G, Fertil B, Navarro C, Pereira S, Cau P, Levy N, et al. Shape and texture indexes application to cell nuclei classification. Int J Pattern Recognit Artif Intell. 2013; 27(01):1357002.

15. Wah YB, Ibrahim N, Hamid HA, Abdul-Rahman S, Fong S. Feature selection methods: case of filter and wrapper approaches for maximising classification accuracy. Pertanika J Sci Technol. 2018; 26(1):329–40.

16. Hameed SS, Petinrin OO, Osman A, Hashi FS. Filterwrapper combination and embedded feature selection for gene expression data. Int J Adv Soft Comput Appl. 2018; 10(1):90–105.

17. Hui KH, Ooi CS, Lim MH, Leong MS, Al-Obaidi SM. An improved wrapper-based feature selection method for machinery fault diagnosis. PLoS One. 2017; 12(12):e0189143.

18. Karim F, Majumdar S, Darabi H. Insights into LSTM fully convolutional networks for time series classification. IEEE Access. 2019; 7:67718–25.

19. Schuster M, Paliwal KK. Bidirectional recurrent neural networks. IEEE Trans Signal Process. 1997; 45(11):2673–81.

20. Ramachandran P, Zoph B, Le QV. Searching for activation functions. In : Proceedings of the 6th International Conference on Learning Representations (ICLR); 2018 Apr30–May 3; Vancouver, Canada.

21. Sultan HH, Salem NM, Al-Atabany W. Multi-classification of brain tumor images using deep neural network. IEEE Access. 2019; 7:69215–25.

22. Machhale K, Nandpuru HB, Kapur V, Kosta L. MRI brain cancer classification using hybrid classifier (SVMKNN). In : Proceedings of 2015 International Conference on Industrial Instrumentation and Control (ICIC); 2015 May 28–30; Pune, India. p. 60–5.

23. Hossin M, Sulaiman MN. A review on evaluation metrics for data classification evaluations. Int J Data Min Knowl Manag Process. 2015; 5(2):1.

24. Alqudah AM, Alquraan H, Qasmieh IA, Alqudah A, Al-Sharu W. Brain tumor classification using deep learning technique: a comparison between cropped, uncropped, and segmented lesion images with different sizes. Int J Adv Trends Comput Sci Eng. 2019; 8(6):3684–91.

25. Pashaei A, Sajedi H, Jazayeri N. Brain tumor classification via convolutional neural network and extreme learning machines. In : Proceedings of 2018 8th International Conference on Computer and Knowledge Engineering (ICCKE); 2018 Oct 25–26; Mashhad, Iran. p. 314–9.

26. Diaz-Pernas FJ, Martinez-Zarzuela M, Anton-Rodriguez M, Gonzalez-Ortega D. A Deep learning approach for brain tumor classification and segmentation using a multiscale convolutional neural network. Healthcare (Basel). 2021; 9(2):153.

27. Swati ZN, Zhao Q, Kabir M, Ali F, Ali Z, Ahmed S, et al. Brain tumor classification for MR images using transfer learning and fine-tuning. Comput Med Imaging Graph. 2019; 75:34–46.

28. Ismael MR, Abdel-Qader I. Brain tumor classification via statistical features and back-propagation neural network. In : Proceedings of 2018 IEEE International Conference on Electro/Information Technology (EIT); 2018 May 3–5; Rochester, MI. p. 252–7.

29. Badza MM, Barjaktarovic MC. Classification of brain tumors from MRI images using a convolutional neural network. Appl Sci. 2020; 10(6):1999.

30. Cheng J, Yang W, Huang M, Huang W, Jiang J, Zhou Y, et al. Retrieval of brain tumors by adaptive spatial pooling and Fisher vector representation. PLoS One. 2016; 11(6):e0157112.

Figure 1

T1-weighted two-dimensional magnetic resonance imaging scans of brain tumors with three different angles: axial (first row), coronal (second row), and sagittal (third row). (A) Glioma. (C) Meningioma. (E) Pituitary tumor. (B, D, and F) Mask images of brain tumors generated from (A), (C), and (E), respectively.

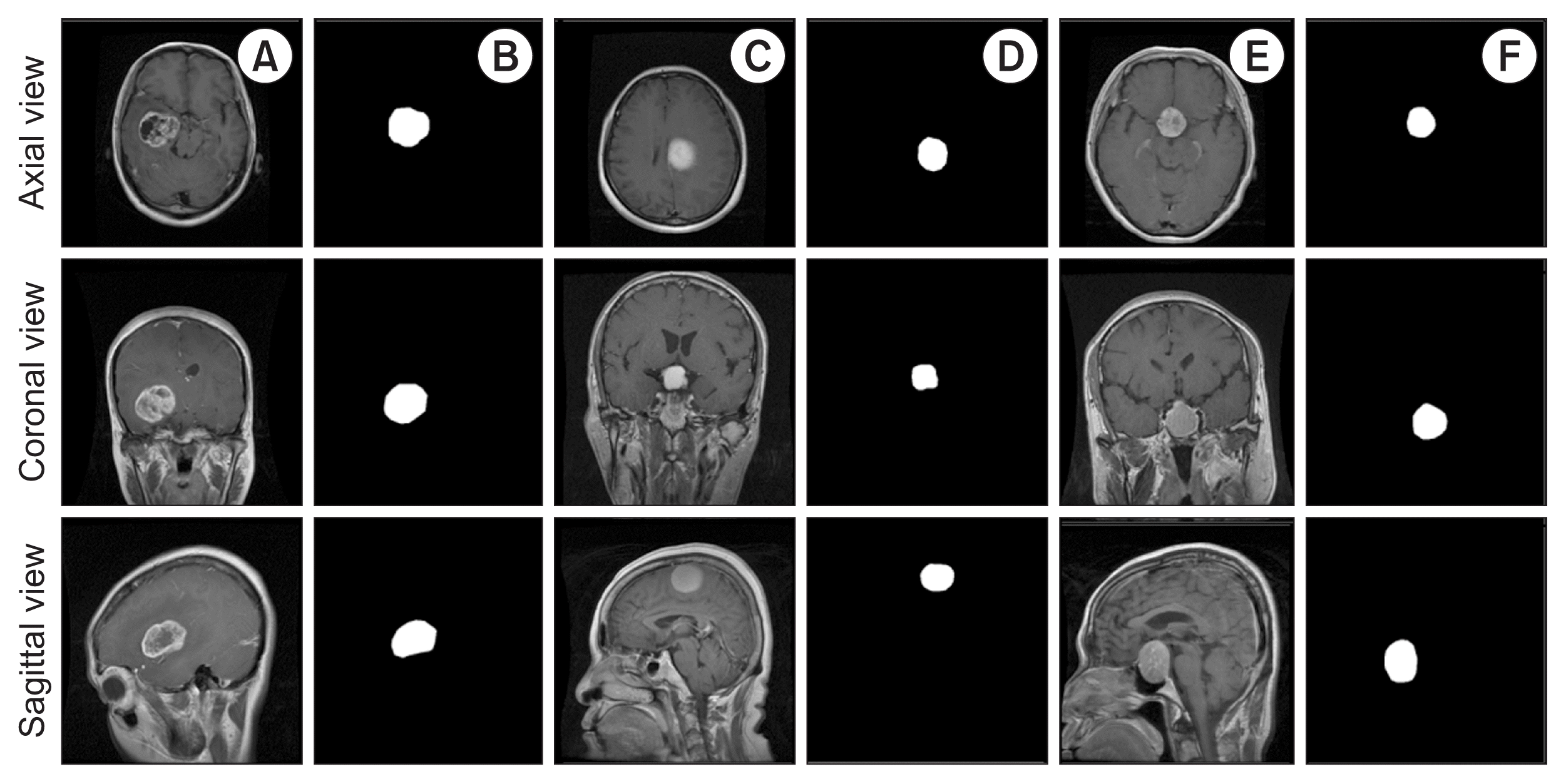
Figure 2

Flowchart of the research pipeline for brain tumor classification. 2D MRI: two-dimensional magnetic resonance imaging, GLCM: gray level co-occurrence matrix, GLRLM: gray level run length matrix, GLSZM: gray level size zone matrix, GLDM: gray level dependence matrix, NGTDM: neighboring gray-tone difference matrix, LSTM: long short-term memory, SVM: support vector machine, KNN: k-nearest neighbor, LR: logistic regression, RF: random forest, LDA: linear discriminant analysis.

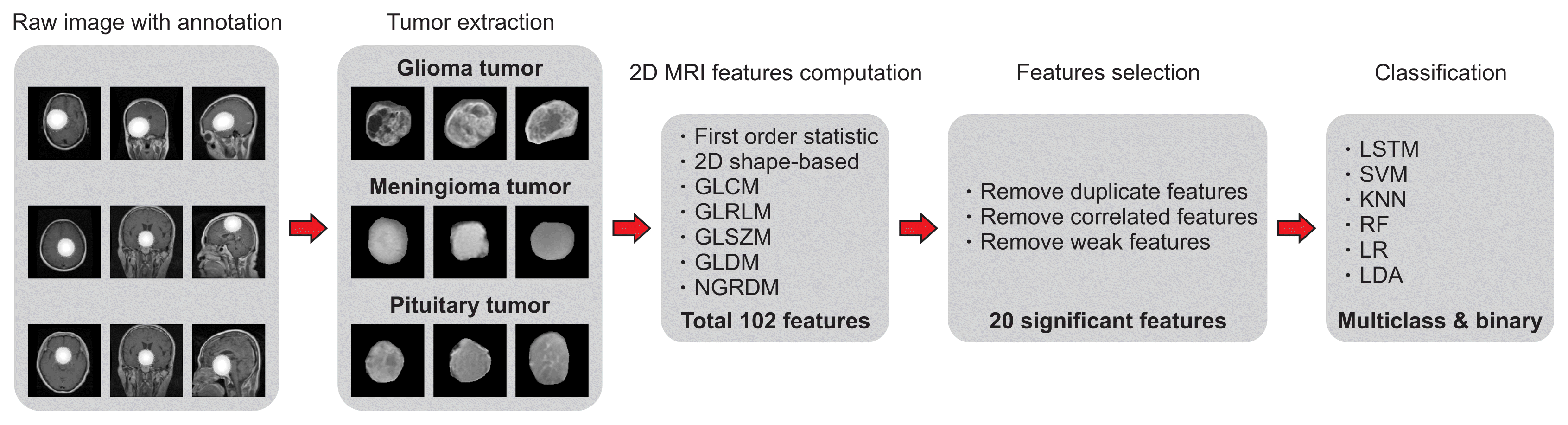
Figure 3

Extraction of regions of interest for three different classes of brain tumors. (A–C) Gliomas. (D–F) Meningiomas. (G–I) Pituitary tumors.

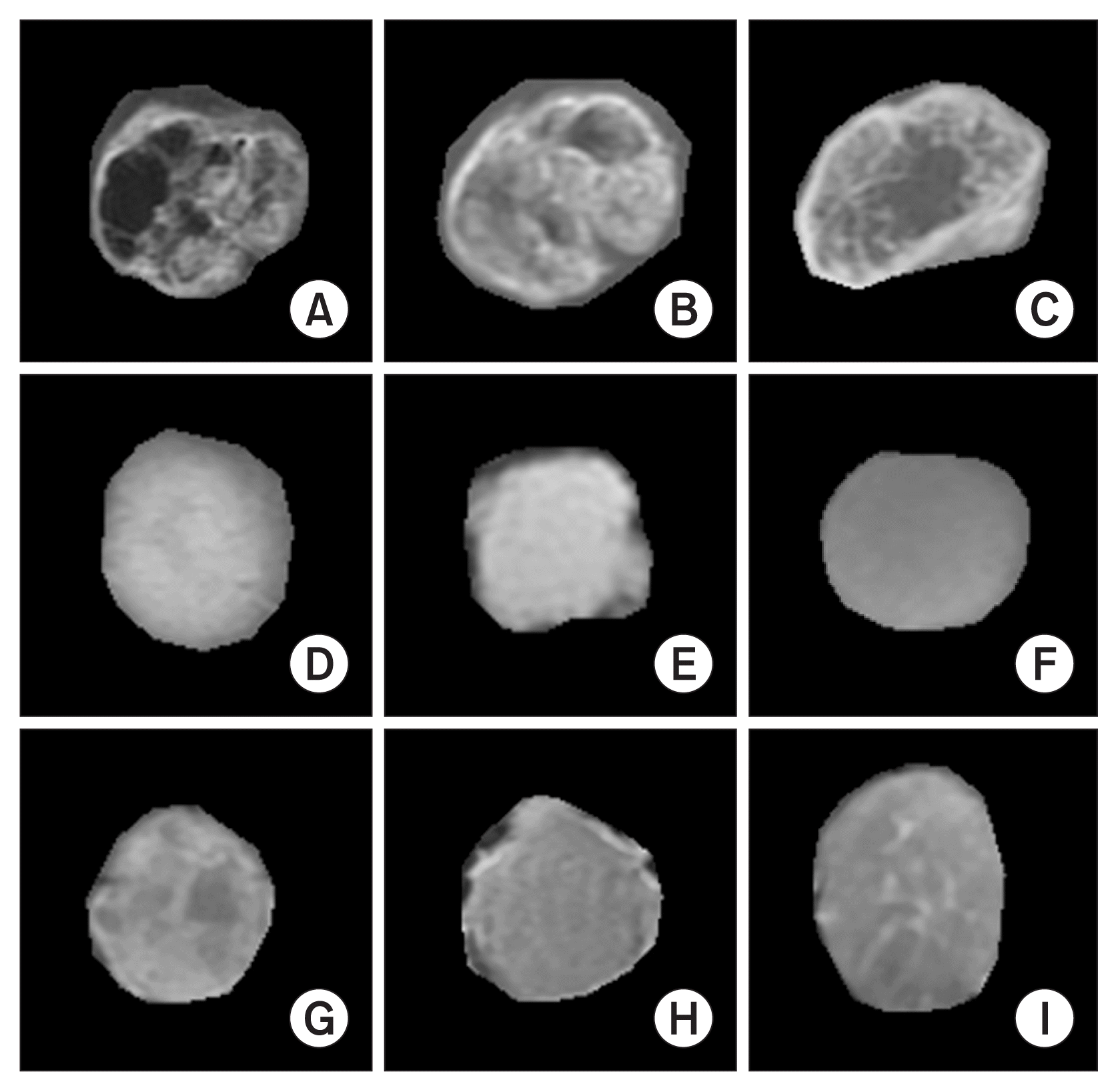
Figure 4

Process of feature engineering and selection. FOS: first-order statistics, 2D: two-dimensional, GLCM: gray level co-occurrence matrix, GLRLM: gray level run length matrix, GLSZM: gray level size zone matrix, GLDM: gray level dependence matrix, NGTDM: neighboring gray-tone difference matrix.

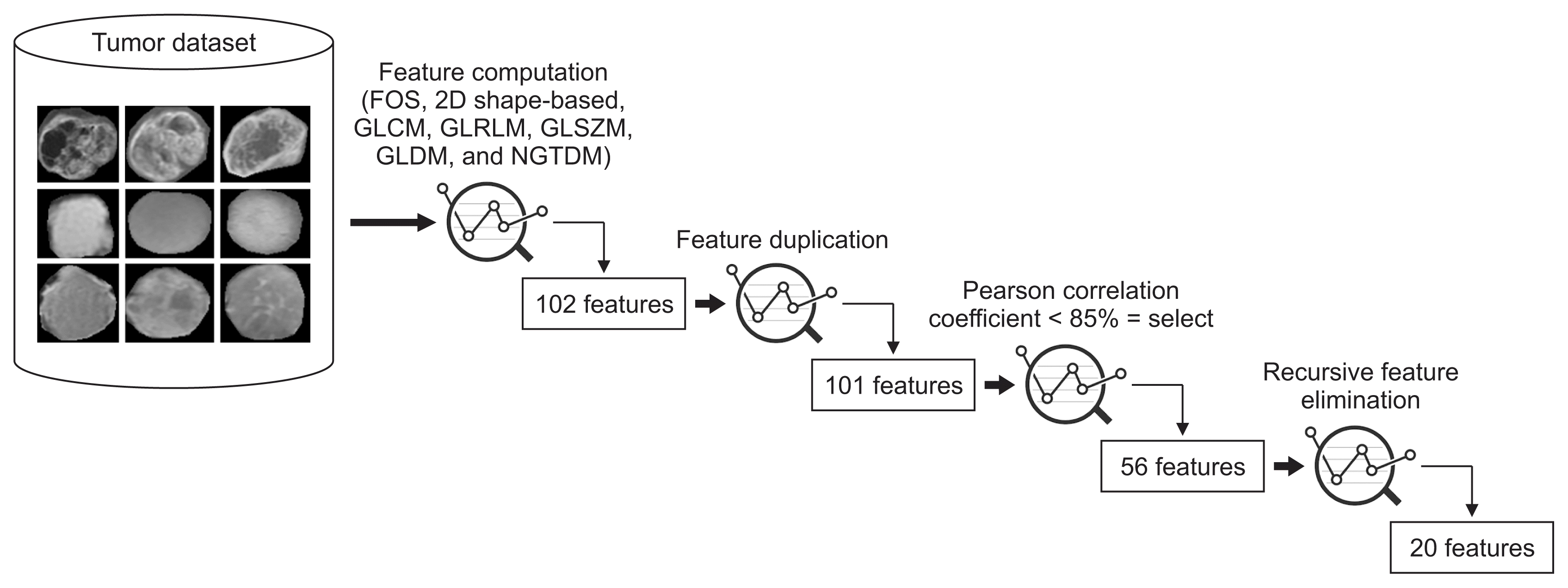
Figure 5

Receive operating characteristic (ROC) curve for analyzing the performance of the models and comparing the results of each classifier. (A) ROC curve of multiclass classification (glioma vs. meningioma vs. pituitary). (B) ROC curve of glioma vs. meningioma classification. (C) ROC curve of glioma vs. pituitary classification. (D) ROC curve of meningioma vs. pituitary classification. LSTM: long short-term memory, SVM: support vector machine, KNN: k-nearest neighbor, LR: logistic regression, RF: random forest, AUC: area under the curve.

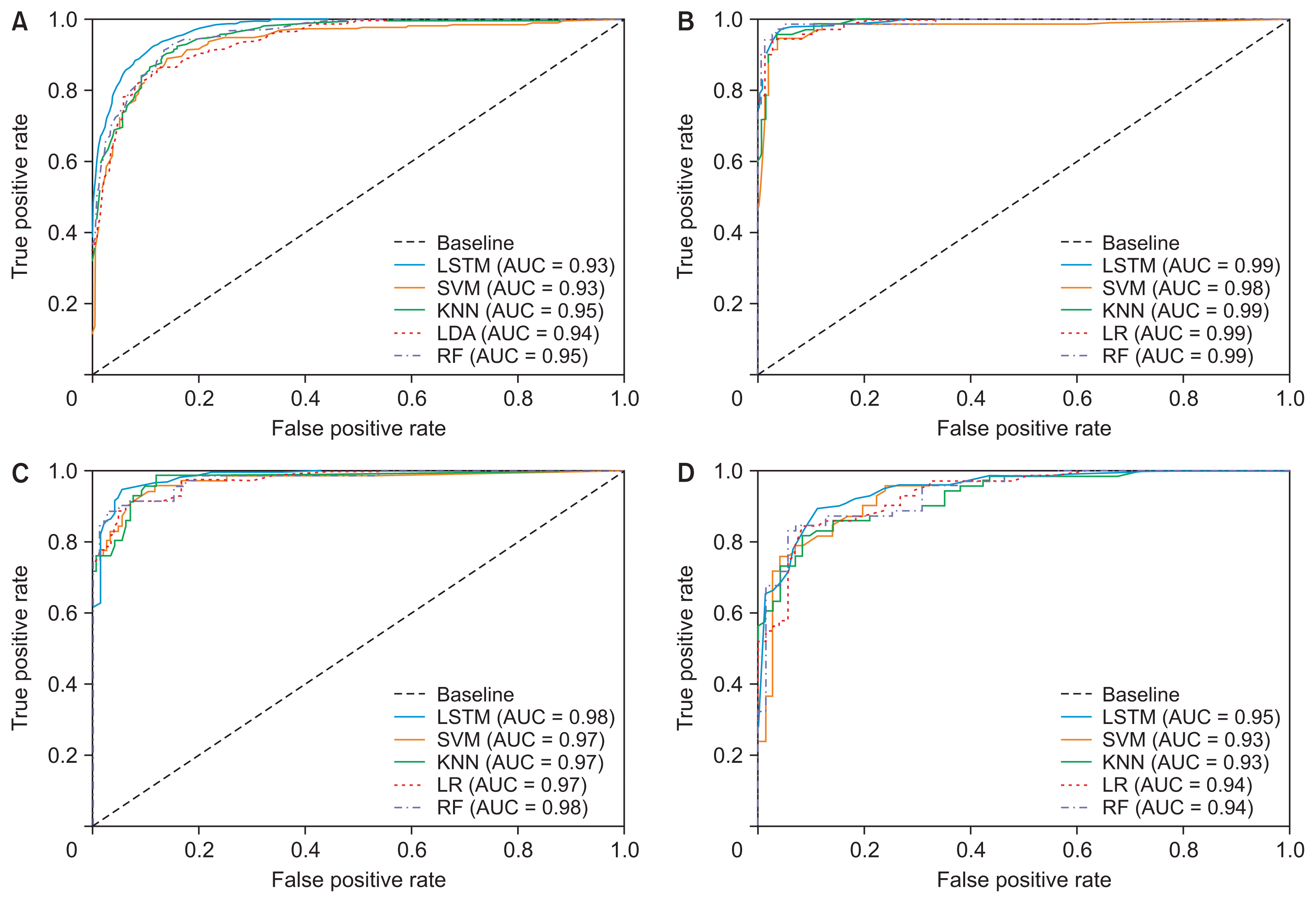
Table 1

List of the significant features and their mathematical description

Skewness	Features
10 Percentile	$10^{t h} & 90^{t h} (L_{p}) = \frac{P}{100} (X + 1)$
90 Percentile
Energy	$e n e r g y = \sum_{i = 1}^{N_{p}} {(X (i) + c)}^{2}$
Kurtosis	$s k e w n e s s = \frac{μ_{3}}{σ^{3}} = \frac{\frac{1}{N_{p}} Σ_{i = 1}^{N_{p}} {(X (i) - \bar{X})}^{3}}{{(\sqrt{\frac{1}{N_{p}} Σ_{i = 1}^{N_{p}} {(X (i) - \bar{X})}^{2}})}^{3}}$
Minimum	minimum = min(X)
Skewness	$s k e w n e s s = \frac{μ_{3}}{σ^{3}} = \frac{\frac{1}{N_{p}} Σ_{i = 1}^{N_{p}} {(X (i) - \bar{X})}^{3}}{{(\sqrt{\frac{1}{N_{p}} Σ_{i = 1}^{N_{p}} {(X (i) - \bar{X})}^{2}})}^{3}}$
Uniformity	$u n i f o r m i t y = \sum_{i = 1}^{N_{g}} p {(i)}^{2}$
Elongation	$e l o n g a t i o n = \sqrt{\frac{λ_{m i n o r}}{λ_{m a j o r}}}$
Major axis length	$m a j o r a x i s = 4 \sqrt{λ_{m a j o r}}$
Pixel surface (area)	$A_{p i x e l} = \sum_{i = 1}^{N_{p}} A_{i}$
Auto correlation	$a u t o c o r r e l a t i o n = \sum_{i = 1}^{N_{g}} \sum_{j = 1}^{N_{g}} p (i, j) i j$
Cluster shade	$c l u s t e r s h a d e = \sum_{i = 1}^{N_{g}} \sum_{j = 1}^{N_{g}} {(i + j - μ_{x} - μ_{y})}^{2} p (i, j)$
Informal measure of correlation (IMC)	$I M C = \sqrt{1 - e^{- 2 (H X Y 2 - H X Y)}}$
Inverse variance	$i n v e r s e v a r i a n c e = \sum_{k = 1}^{N_{g} - 1} \frac{P_{x - y} (k)}{k^{2}}$
Joint average	$μ_{x} = \sum_{i = 1}^{N_{g}} \sum_{j = 1}^{N_{g}} p (i, j) i$
Joint energy	$j o i n t e n e r g y = \sum_{i = 1}^{N_{g}} \sum_{j = 1}^{N_{g}} {(p (i, j))}^{2}$
Maximal correlation coefficient (MCC)	$M C C = \sqrt{s e c o n d l a r g e s t e i g e n v a l u e o f Q}$ $Q (i, j) = \sum_{k = 0}^{N_{g}} \frac{p (i . k) p (j, k)}{P_{x} (i) P_{y} (k)}$
Gray level variance (GLV)	$G L V = \sum_{i = 1}^{N_{g}} \sum_{j = 1}^{N_{g}} (p (i, j) {(i - μ)}^{2}$
High gray level run emphasis (HGLRE)	$H G L R E = \frac{Σ_{i = 1}^{N_{g}} Σ_{j = 1}^{N_{r}} \frac{P (i, j ∣ θ)}{i^{2} j^{2}}}{N_{r} (θ)}$
Large area low gray level emphasis (LALGLE)	$L A L G L E = \frac{Σ_{i = 1}^{N_{g}} Σ_{j = 1}^{N_{s}} \frac{P (i, j) j^{2}}{i^{2}}}{N_{z}}$

Table 2

Dataset splitting for LSTM and ML classification

Tumor class	Training	Testing	Total slices	Total patients
Glioma	1,283	143	1,426	91
Meningioma	637	71	708	82
Pituitary	837	93	930	60
Total slices & patients	2,757	307	3,064	233

LSTM: long short-term memory, ML: machine learning.

Table 3

The overall performance of multiclass and binary classification based on six different algorithms (unit: %)

Classification	Groups	Metrics	LSTM	SVM	KNN	LR	RF	LDA
Multiclass	Glioma vs. Meningioma vs. Pituitary	Accuracy	80.1	82.7	83.1	-	84.0	81.7
		Recall	78.3	80.3	81.3	-	81.9	78.7
		Precision	78.3	81.0	81.7	-	81.8	79.7
		F1-score	78.3	80.7	81.7	-	81.7	79.3
		Kappa coefficient	68.8	72.7	73.5	-	74.9	71.1
Binary	Glioma vs. Meningioma	Accuracy	97.7	94.9	95.8	95.8	97.2	-
		Recall	97.2	94.0	95.1	95.1	96.5	-
		Precision	97.5	94.3	95.4	95.4	97.2	-
		F1-score	97.0	94.0	95.5	95.5	97.0	-
		Kappa coefficient	94.7	88.4	90.5	90.5	93.6	-
	Glioma vs. Pituitary Accuracy	93.9	91.5	90.6	92.5	94.3	-
		Recall	92.3	90.0	89.4	91.2	92.9	-
		Precision	93.9	91.0	89.5	91.8	94.2	-
		F1-score	93.5	90.5	89.5	91.5	93.5	-
		Kappa coefficient	86.1	80.8	78.9	83.0	87.2	-
	Meningioma vs. Pituitary	Accuracy	85.9	83.8	82.4	85.2	85.9	-
		Recall	86.0	84.3	82.4	85.2	85.9	-
		Precision	86.2	84.4	82.6	85.2	85.9	-
		F1-score	85.5	84.0	82.5	85.0	86.0	-
		Kappa coefficient	71.8	67.6	64.8	70.4	71.8	-

LSTM: long short-term memory, SVM: support vector machine, KNN: k-nearest neighbor, LR: logistic regression, RF: random forest, LDA: linear discriminant analysis.

Table 4

Comparison of the computation costs of learning algorithms based on training and testing (unit: second)

Groups	Learning algorithms	Feature selection
		Before	After
		Glioma vs. Meningioma vs. Pituitary	LSTM	9,120	2,107
SVM	29		6
KNN	13		3
LDA	3		2
RF	7		4
Glioma vs. Meningioma	LSTM	7,800	1,467
	SVM	11	2
	KNN	6	2
	LR	8	1
	RF	5	3
Glioma vs. Pituitary	LSTM	6,600	1,387
	SVM	14	3
	KNN	7	2
	LR	10	1
	RF	5	2
Meningioma vs. Pituitary	LSTM	5,400	990
	SVM	7	2
	KNN	4	1
	LR	8	1
	RF	5	2

LSTM: long short-term memory, SVM: support vector machine, KNN: k-nearest neighbor, LDA: linear discriminant analysis, RF: random forest, LR: logistic regression.

Table 5

Comparison between other state-of-the-art approaches and our method

Approach	Features	Classification type	Classifier	Accuracy (%)
Cheng et al. [10]	Intensity histogram	Multiclass	SVM	87.5
	GLCM	Multiclass	SVM	89.7
	Bag-of-words	Multiclass	SVM	91.3
Sultan et al. [21]	CNN-based	Multiclass	2D CNN	96.1
Alqudah et al. [24]	CNN-based	Multiclass	2D CNN	99.0
Pashaei et al. [25]	CNN-based	Multiclass	2D CNN	93.7
Diaz-Pernas et al. [26]	CNN-based	Multiclass	Multiscale CNN	97.3
Swati et al. [27]	CNN-based	Multiclass	Pretrained 2D CNN	94.8
Ismael and Abdel-Qader [28]	Statistical (DWT and Gabor filter)	Multiclass	BPNN	91.8
Badza and Barjaktarovic [29]	CNN-based	Multiclass	2D CNN	96.6
Cheng et al. [30]	Bag-of-words and Fisher vector	Multiclass	Fisher kernel	94.7
Proposed	FOS, GLCM, GLRLM, GLSZM, GLDM, NGTDM, 2D Shape	Meningioma vs. glioma vs. pituitary (multiclass)	RF	84.0
Proposed		Meningioma vs. glioma (binary)	LSTM	97.7

GLCM: gray level co-occurrence matrix, SVM: support vector machine, CNN: convolutional neural network, 2D: two-dimensional, DWT: discrete wavelet transform, BPNN: back-propagation neural network, FOS: first-order statistics, GLRLM: gray level run length matrix, GLSZM: gray level size zone matrix, GLDM: gray level dependence matrix, NGTDM: neighboring gray-tone difference matrix, RF: random forest, LSTM: long short-term memory.

TOOLS

Similar articles