Derivation of pharmacokinetic equations

규정 노

doi:10.17085/apm.2018.13.4.349

Abstract

A variety of drugs are continuously or intermittently administered to patients during general or regional anesthesia. Pharmacotherapy should also receive priority compared with several treatment modalities including nerve blocks for chronic pain control. Therefore, pharmacology may be fundamental to anesthesia as well as pain medicine. Pharmacokinetic equations quantitatively evaluating drug transfer in the body are essential to understanding pharmacological principles. In mammillary compartmental models, pharmacokinetic equations are easily derived from a few simple principles. The kinetics of drug transfer between compartments is determined initially. Ordinary, linear differential equations are constructed based on the kinetics. The Laplace transforms of these differential equations are used to derive functions for the calculation of drug amounts in the central or effect compartments in the Laplace domain. The inverse Laplace transforms of these functions are used to obtain pharmacokinetic equations in time domain. In this review, a two-compartment mammillary pharmacokinetic model is used to derive pharmacokinetic equations using the aforementioned principles.

전신마취나 부위마취를 하는 동안 여러 종류의 약물을 지속적으로 혹은 간헐적으로 투여하며, 통증의학 역시 약물치료가 기본이 되므로, 마취통증의학과는 약물을 많이 사용하는 과에 속한다. 따라서, 약리는 마취통증의학과의 기본 학문이라고 할 수 있으며, 마취통증의학과 의사는 약리의 기본원리를 충분히 이해할 필요가 있다.

약리를 이해하는 데 있어서 기본이 되는 것은 약동학 수식이다. 약동학 수식은 체내에서 약물의 이동을 정량적으로 규명해 주는데, 몇 가지 원리만 알면 쉽게 유도할 수 있다.

그 원리란, 너무 간단해서 다음의 한 문장으로 요약할 수 있다. 구획간 약물 이동 역학(kinetics)을 파악하고, 이를 바탕으로 구획별 약물량 변화에 대한 미분방정식을 만든 다음, 라플라스 변환(Laplace transform), 역라플라스 변환(inverse Laplace transform)하여, 시간에 따르는 약물량 함수를 만들어 낸다.

수식이 많아서 일견 어려워 보이나, 파고 들어가 보면 위 원리 외에 아무 것도 아니다. 여기서는 이구획 유선약동학 모형(two compartment mammillary pharmacokinetic model)을 예로 들어 설명하고자 한다.

약동학 수식유도를 이해하기 위하여 필요한 수학

라플라스 변환(Laplace transform)

라플라스 변환은 적분변환(integral transform)의 일종이다. 적분변환은 다음과 같은 형태의 변환, T로 나타낸다.

T (f (u)) = \int_{t_{1}}^{t_{2}} K (t, u) f (t) d t

이 변환의 입력은 함수 f(t)이며 출력은 T(f(u))이다. 변수 t, u의 함수인 K를 커널함수(kernel function)라고 한다. 즉, 커널함수는 입력함수의 변수 t와 출력함수의 변수 u 모두를 포함하고 있다. 입력함수 변수 t에 대하여 위 식을 적분하면, t는 전부 숫자로 바뀌고, 변수는 u만 남게 됨으로써, 결국 t에 대한 함수 f(t)가 u에 대한 함수 T(f(u))로 변환된다.

일부 커널(kernel)은 역변환(inverse transform)을 시켜주는 역커널(inverse kernel), K⁻¹(u, t)를 가질 수 있다. 역변환은 아래와 같다.

f (T) = \int_{u_{1}}^{u_{2}} K^{- 1} (t, u) (T (f (u))) d u

역변환에서 입력함수는 T(f(u))이며, 출력함수는 f(t)이다. 입력함수 변수 u에 대하여 위 식을 적분하면, u는 전부 숫자로 바뀌고, 변수는 t만 남게 됨으로써, 결국 u에 대한 함수 T(f(u))는 t에 대한 함수 f(t)로 변환된다.

시간함수(time function), f(t)가 있다고 하자. 이때 t ≥ 0이다. 함수 f(t)의 라플라스 변환은 L{f(t)}로 표기하며, 다음과 같다.

L {f (t)} = \int_{0}^{\infty} f (t) e^{- s t} d t

로, 여기서 e^−st가 커널함수이다

위에서 설명하였듯이, 모든 적분변환은 원래의 함수를 변환하기 위하여 커널함수를 사용하며, 커널함수의 종류에 따라서 그 적분변환의 명칭이 정해진다. 따라서 라플라스 변환은 e^−st를 커널함수로 하는 적분변환의 일종이다. 생체신호분석에 많이 사용되는 푸리에 변환(Fourier transform)도 적분변환의 일종이며,

\frac{e^{- i u t}}{\sqrt{2 π}} (- \infty < t < \infty, - \infty < u < \infty)

를 커널함수로 하여, 시계열(time series)의 생체신호(biosignal)를 주파수 대역(frequency band)별 파워(power)로 변환한다.

라플라스 변환 역시 이와 유사하게 시계열 함수를 주파수의 함수로 변환하는데 사용된다고 보면 된다. 연산자(operator) s는 주파수 변수(frequency variable)이며 단위는 sec⁻¹이다. t는 시간 변수(time variable)이며 단위는 sec이다. 따라서 st는 단위가 없다.

간단한 예를 들어서 설명하도록 하겠다.

먼저 다음과 같음을 알아 두자.

\int e^{k - t} d t = \frac{1}{k} e^{k - t} + C

시계열 함수 f(t)=e^t를 라플라스 변환(L{f(t)})하면, 정의상 다음과 같다.

\begin{array}{l} f (t) = e^{t} \\ L {f (t)} = \int_{0}^{\infty} e^{t} e^{- s t} d t = \int_{0}^{\infty} e^{{(1 - s)}^{t}} d t = {[\frac{1}{1 - s} e^{{(1 - s)}^{t}}]}_{0}^{\infty} = 0 - \frac{1}{1 - s} = \frac{1}{s - 1} \end{array}

위에서,

\lim_{x \to - \infty} e^{x} = 0

임을 안다면, 시간 t = ∞일 때 0이 되는 것을 이해할 수 있을 것이다. 결론적으로 L(e^t) = 1/(s−1)이다. 라플라스 변환을 하면, 함수의 복잡도가 감소하여 계산이 쉬워진다는 것을 알 수 있다.

미분방정식의 라플라스 변환은 L{f′(t)}=sL{f(t)} − f(0)이다.

이에 대한 증명은 다음과 같다.

미분 가능한 연속함수 f(x)와 g(x)에 대하여, 적분 구간이 [a, b]일 때, 다음과 같은 부분적분법(integration by parts)으로 표현할 수 있다.

\int_{a}^{b} g (x) h^{'} (x) d x = {[g (x) h (x)]}_{a}^{b} - \int_{a}^{b} g^{'} (x) h (x) d x

미분방정식의 라플라스 변환은 다음과 같다.

L {f^{'} (t)} = \int_{0}^{\infty} e^{- s t} f^{'} (t) d t

위 식에서

g (X) \to e^{- s t}, h^{'} (X) \to f^{'} (t)

라고 보면 된다.

먼저 다음과 같은 지수함수의 미분에 대하여 알아 두자.

\begin{array}{l} y = e^{f (x)} \\ y^{'} = f^{'} (x) \cdot e^{f (x)} \\ (e^{- s \cdot t})^{'} = - s \cdot e^{- s \cdot t} \end{array}

위의 지수함수 미분을 참고하여 미분방정식의 라플라스 변환을 부분적분법으로 풀어보자.

\begin{array}{l} L {f^{'} (t)} \\ = \int_{0}^{\infty} e^{- s t} f^{'} (t) d t \\ = {[e^{- s t} f (t)]}_{0}^{\infty} + \int_{0}^{\infty} s e^{- s t} f (t) d t \\ = - f (0) + s \int_{0}^{\infty} e^{- s t} f^{'} (t) d t \\ = s L {f (t)} - f (0) \end{array}

약동학의 구획 모형에서는, 속도상수와 구획 내 약물량을 이용하여, 구획별로 시간에 따르는 약물량의 변화를 계산한다. 구획마다 약물량의 변화를 선형 상미분방정식(ordinary, linear differential equation)으로 기술할 수 있으므로, 미분방정식의 개수는 구획 수와 동일하다. 이와 같은 연립 미분방정식을 전부 라플라스 변환하고, 구하고자 하는 구획에 대하여 재정렬한 후, 이를 다시 역라플라스 변환하면 적분된 형태의, 시간에 따르는 구획별 약물량 함수를 얻을 수 있다. 앞으로 구획모형마다 실제 계산을 어떻게 하는지에 대하여 자세하게 기술할 것이다.

크레머 공식(Cramer’s rule)

연립방정식을 풀기 위하여 크레머 공식을 이용한다. 크레머 공식을 간단하게 소개하면 다음과 같다.

\begin{array}{l} a x + b y = e \\ c x + d y = f \\ [\begin{array}{l} a & b \\ c & d \end{array}] [\begin{matrix} x \\ y \end{matrix}] = [\begin{matrix} e \\ f \end{matrix}] \\ x = \frac{| \begin{matrix} e & b \\ f & d \end{matrix} |}{| \begin{matrix} a & b \\ c & d \end{matrix} |} = \frac{e d - b f}{a d - b c}, y = \frac{| \begin{matrix} a & e \\ c & f \end{matrix} |}{| \begin{matrix} a & b \\ c & d \end{matrix} |} = \frac{a f - c e}{a d - b c} \\ D = [\begin{matrix} a & b \\ c & d \end{matrix}], D_{1} = [\begin{matrix} e & b \\ f & d \end{matrix}], D_{2} = [\begin{matrix} a & e \\ c & f \end{matrix}] \\ x = \frac{| D_{1} |}{| D |}, y = \frac{| D_{2} |}{| D |} \end{array}

크레머 공식은 구획별 약물량 변화를 나타내는 연립 미분방정식에서 각 구획의 약물량을 구하는 데 사용한다.

베넷(Benet)의 일반 부분분수 정리(general partial fraction theorem)

구획별 약물량 변화를 나타내는 연립 미분방정식을 라플라스 변환하고, 이를 역라플라스 변환하여 구획별로 시간에 따르는 약물량 함수를 유도하는데, 베넷의 일반 부분분수 정리는 역라플라스 변환을 쉽게 수행할 수 있게 해준다.

L^{- 1} {\frac{N (s)}{D (s)}} = \sum_{i = 1}^{n} \frac{N (- λ_{i})}{D (- λ_{i})} \cdot e - λ_{i} \cdot t

좌변의 s 영역(domain)을 우변의 시간 영역(time domain)으로 변환할 수 있으려면, 즉 역라플라스 변환(L⁻¹)을 하려면, 분모 D(s)가 분자 N(s)보다 s에 대하여 차수가 더 높은 다항식이라야 한다. 또한, 분모를 인수분해 하였을 때 동일 인수가 반복되지 말아야 한다. 이를 베넷의 일반 부분분수 정리(general partial fraction theorem) 혹은 지문법(finger print method)이라고 한다[1]. 먼저 분모 D(s)의 근(root)으로 N(s), D(s)에 있는 모든 s를 치환한 후 e^rootㆍt를 곱해준다. D(s)는 다항식이므로 근이 여러 개 있을 것이다. 근마다 이와 같은 과정을 반복하여 그 결과들을 전부 더한다.

아래는 베넷의 일반 부분분수 정리에 대한 증명이다. 일반적으로 다음과 같은 부분분수 분해(partial fraction decom춑osition) 혹은 부분분수 전개(partial fraction expansion)을 사용하면 유리식(분자, 분모가 다항식인 분수) 내 분자나 분모의 차수를 낮출 수 있다.

A, B를 상수라고 할 때 다음의 유리식을

\frac{c x + d}{(x + a) (x + b)}

부분분수 분해를 하면, 다음과 같다.

\frac{c x + d}{(x + a) (x + b)} = \frac{A}{x + a} + \frac{B}{x + b}

위 식을 정리하면

\begin{matrix} \frac{c x + d}{(x + a) (x + b)} = \frac{A}{x + a} + \frac{B}{x + b} \\ c x + d = A \cdot (x + b) + B \cdot (x + a) \end{matrix}

이다.

예를 들어

\frac{1}{(x + 1) (x - 1)}

을 부분분수 분해하면 다음과 같다.

\frac{1}{(x + 1) (x - 1)} = \frac{A}{x + 1} + \frac{B}{x - 1}

위 식을 정리하면 다음과 같다.

1 = A \cdot (x - 1) + B \cdot (x + 1)

x = 1이라면, 2B = 1, B = 1/2.

x = −1이라면, −2A = 1, A = −1/2.

이와 유사하게 다음 유리식을

\frac{s + k_{21}}{(s + λ_{1}) (s + λ_{2})}

부분분수 분해하면

\frac{s + k_{21}}{(s + λ_{1}) (s + λ_{2})} = \frac{A}{s + λ_{1}} + \frac{B}{s + λ_{2}}

위 식을 정리하면

s + k_{21} = A \cdot (s + λ_{2}) + B \cdot (s + λ_{1})

1) s=λ₁

\begin{matrix} - λ_{1} + k_{21} = A \cdot (- λ_{1} + λ_{2}) \\ A = \frac{- λ_{1} + k_{21}}{λ_{1} + λ_{2}} = \frac{- λ_{1} - k_{21}}{λ_{1} - λ_{2}} \end{matrix}

2) s=λ₂

\begin{matrix} - λ_{2} + k_{21} = B \cdot (- λ_{2} + λ_{1}) \\ B = \frac{- λ_{2} + k_{21}}{λ_{2} + λ_{1}} = \frac{k_{21} - λ_{2}}{λ_{1} - λ_{2}} \end{matrix}

따라서

\begin{matrix} \frac{s + k_{21}}{(s + λ_{1}) (s + λ_{2})} = \frac{λ_{1} - k_{21}}{λ_{1} - λ_{2}} \cdot \frac{1}{s + λ_{1}} + \frac{k_{21} - λ_{2}}{λ_{1} - λ_{2}} \cdot \frac{1}{s + λ_{2}} \\ L^{- 1} [\frac{s + k_{21}}{(s + λ_{1}) (s + λ_{2})}] = L^{- 1} [\frac{λ_{1} - k_{21}}{λ_{1} - λ_{2}} \cdot \frac{1}{s + λ_{1}} + \frac{k_{21} - λ_{2}}{λ_{1} - λ_{2}} \cdot \frac{1}{s + λ_{2}}] \end{matrix}

한편,

L^{- 1} [\frac{1}{(s + α)}] = e^{- α \cdot t}

이고,

A = \frac{λ_{1} - k_{21}}{λ_{1} - λ_{2}}

B = \frac{k_{21} - λ_{2}}{λ_{1} - λ_{2}}

는 상수이므로,

\begin{array}{l} L^{- 1} [\frac{λ_{1} - k_{21}}{λ_{1} - λ_{2}} \cdot \frac{1}{s + λ_{1}} + \frac{k_{21} - λ_{2}}{λ_{1} - λ_{2}} \cdot \frac{1}{s + λ_{2}}] \\ = \frac{λ_{1} - k_{21}}{λ_{1} - λ_{2}} \cdot L^{- 1} (\frac{1}{s + λ_{1}}) + \frac{k_{21} - λ_{2}}{λ_{1} - λ_{2}} \cdot L^{- 1} (\frac{1}{s + λ_{2}}) \\ \frac{λ_{1} - k_{21}}{λ_{1} - λ_{2}} \cdot e^{- λ_{1} \cdot t} + \frac{k_{21} - λ_{2}}{λ_{1} - λ_{2}} \cdot e^{- λ_{2} \cdot t} \end{array}

따라서

L^{- 1} [\frac{s + k_{21}}{(s + λ_{1}) (s + λ_{2})}] = \frac{λ_{1} - k_{21}}{λ_{1} - λ_{2}} \cdot e^{- λ_{1} \cdot t} + \frac{k_{21} - λ_{2}}{λ_{1} - λ_{2}} \cdot e^{- λ_{2} \cdot t}

이다.

즉, 분모가 분자보다 s에 대하여 차수가 더 높은 다항식이고, 분모를 인수분해 하였을 때 동일 인수가 반복되지 않는다는 전제 하에서, 분모의 근(root, 위의 경우 −λ₁, −λ₂)으로 분자 및 분모의 모든 s를 치환한 후 e^rootㆍt를 곱해준다. 근마다 이와 같은 과정을 반복하여 그 결과들을 전부 더한다.

약물의 역학(KINETICS)

약동학을 흔히 약물의 ADME라고 하는데, 이는 absorption (흡수), distribution (분포), metabolism (대사) 그리고 excretion (배설)을 의미한다(Fig. 1). 대사와 배설을 제거(elimination)라고 하며, 분포와 제거를 배치(disposition)라고 한다.

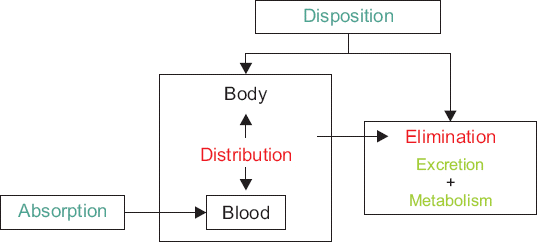Fig. 1

ADME (absorption, distribution, metabolism and excretion).

약물이 체내에서 움직이는 방식을 역학이라고 한다. 흡수, 분포, 제거 과정에서 약물의 역학이 어떤 종류인가에 따라서, 약동학 구획 내 약물량 변화를 기술하는 미분방정식이 달라지고, 이로부터 유도되는 약동학 수식도 달라진다.

영차역학(zero-order kinetics)

영차역학이란 약물이 단위 시간당 일정한 양이 소실(또는 유입)되는 것을 말한다. 현재 체내에 100 mg의 약물이 있고, 이 약물이 영차역학을 따르되, 시간당 10 mg씩 없어진다고 가정하자. 그러면 한 시간 후에는 90 mg, 두 시간 후에는 80 mg, 세 시간 후에는 70 mg이 체내에 남아 있게 될 것이다. 이것을 그래프로 그려 보면 Fig. 2의 좌측 그래프와 같을 것이다. 약물마다 분포용적(volume of distribution)은 불변하는 것으로 간주하므로, 약물의 양을 분포용적으로 나누면 농도가 된다. 따라서 시간과 약물량과의 관계는 시간, 농도 관계와 동일하다고 볼 수 있다.

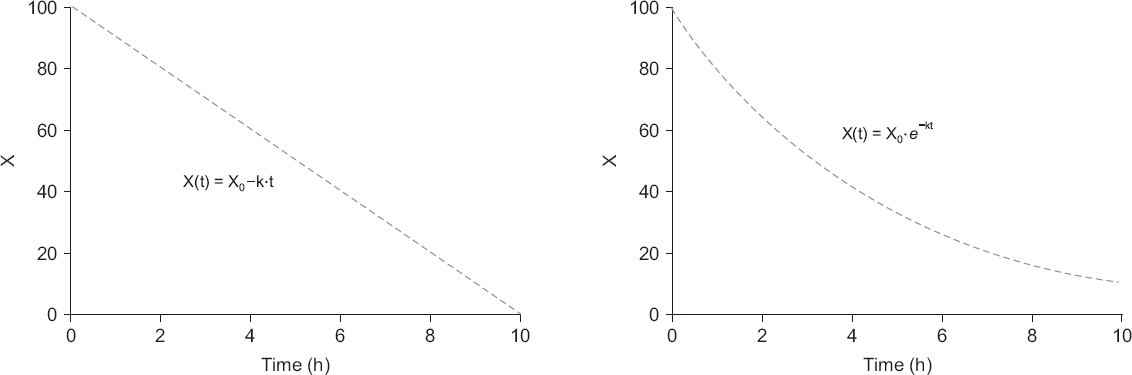Fig. 2

Zero-order (left panel) and first-order (right panel) kinetics. X: amount of a drug. t: time in h. X₀ = 100 mg, k: elimination rate constant (mgㆍh⁻¹ for zero-order kinetics and h⁻¹ for first-order kinetics).

일차역학(first-order kinetics)

영차역학은 매우 간단하고 선형적(linear)이다. 그러나 불행하게도 영차역학에 따라서 소실되는 약물은 흔하지 않다. 대부분의 약물은 일차역학에 의하여 소실된다. 일차역학이란 현재 체내에 남아 있는 약물량인 X(t)의 일정 분율만큼, 약물이 단위시간당 소실(또는 유입)되는 것을 말한다(약물량 변화율의 부호가 소실될 경우는 음, 유입될 경우는 양이 될 것이다).

현재 체내에 100 mg의 약물이 있고 시간당 20%씩 약물이 소실된다고 하면, 한 시간 후에는 100 − 100 × 0.2 mg (80 mg), 두 시간 후에는 80 − 80 × 0.2 mg (64 mg), 세 시간 후에는 64 − 64 × 0.2 mg (51.2 mg)이 체내에 남아 있게 될 것이다. 이것은 Fig. 2의 우측 그래프와 같이 지수함수 곡선으로 나타난다. 약동학의 모든 비극이 이 지수함수로부터 파생한다고 하여도 과언이 아니다. 지수함수는 대표적인 비선형(nonlinear) 수식이고 비선형일 경우 계산하기가 선형수식만큼 간단하지가 않기 때문이다. 그러면 왜 일차역학은 지수함수적 감소를 하는지 수학적으로 살펴 보자.

일차역학 약물이 체내에서 소실될 경우 미분방정식은 아래와 같다.

\frac{d X (t)}{d t} = - k X (t)

위와 같은 미분방정식의 라플라스 변환은, 먼저 좌변의

\frac{d}{d t}

를 s로 바꾸고, 양변의 시간 t를 전부 라플라스 연산자 s로 바꾼다. 마지막으로 좌변에서 X(t)의 초기값, 즉 t=0에서의 X (amount)인 X(0)를 빼 준다.

s X (s) - X (0) = - k X (s)

X (s) = \frac{X (0)}{s + k}

위 식을 역라플라스 변환하면, 시간에 따르는 약물량 함수를 얻을 수 있는데, 역라플라스 변환은 라플라스 변환표를 이용하는 방법,¹⁾ 매트랩(matlab) 등을 이용하여 직접 계산하는 방법, 베넷의 일반 부분분수 정리를 이용하는 방법이 있다.

라플라스 변환표에서, 1/(s + a)의 시간함수는 e^−aㆍt이다. 위 식에서 X(0)는 단순히 곱해주면 되고, k=a로 놓으면

X (t) = X (0) \cdot e^{- k \cdot t}

이다.

위와 같은 역라플라스 변환을 매트랩에서 수행하면 다음과 같다.

>> syms X0 k s t; symbolic variable을 X0, k, s, t로 한다는 의미이다. 여기서 X0는 위 식의 X(0)이다.

>> ilaplace(X0/(s+k)); X0/(s+k)를 역라플라스 변환하라는 의미이다.

ans = X0 * \exp (- k * t); X (0) \cdot e^{- k \cdot t}

X(t)=X(0)·e^-k·t에서

시간 t=0일 경우,

X (t) = X (0) \cdot e^{- k \cdot 0} = X_{0} \cdot 1 = X_{0}

시간 t=∞일 경우

X (t) = X_{0} \cdot e^{- k \cdot \infty} = X_{0} \cdot 0 = 0

즉, e^−kㆍt는 (0, 1) 사이의 값을 가지며, t 시간 동안 일차역학으로 약물이 제거되고 현재 체내에 남아 있는 약물의, 초기량 X(0)에 대한 분율을 의미한다. 일차역학으로 t 시간 동안 제거된 약물의, 초기량에 대한 분율은 (1 − e^−kㆍt)이다.

Fig. 2 우측의 지수함수 곡선을 선형적으로 표현하려면, 양변에 자연대수(natural logarithm)를 취하면 된다.

In X (t) = In X_{0} - k \cdot t

제거속도상수(elimination rate constant) k는 위 수식에 의한 직선의 기울기이다.

투여 경로별 라플라스 영역 입력함수 (INPUT FUNCTION, In_s)

단회정주

In_S = Dose

영차지속정주

DUR을 영차지속정주 시간, Rate를 영차지속정주속도라고 하자.

\begin{array}{l} t \leq D U R \\ R a t e > 0 \end{array}

\begin{array}{l} t > D U R \\ R a t e = 0 \end{array}

영차지속정주 때 라플라스 영역의 입력함수는 시간함수인 Rate를 라플라스 변환한 것이다.

I n_{s} = L (\frac{d X (t)}{d t}) = \int_{0}^{D U R} R a t e \cdot e^{- s t} d t + \int_{D U R}^{\infty} R a t e \cdot e^{- s t} d t

지속정주 중(t ≤ DUR)에는 Rate > 0, DUR 이후 시간에는 Rate = 0이므로,

\begin{array}{l} I n_{s} = {[- \frac{R a t e}{s} e^{- s t}]}_{0}^{D U R} \\ = - \frac{R a t e}{s} \cdot (e^{- s \cdot D U R} - 1) = \frac{R a t e}{s} \cdot (1 - e^{- s . D U R}) \end{array}

이구획 약동학 모형

모형 도식

이구획 모형은 중심구획과 말초구획이 일차역학으로 연결되고, 약물은 중심구획에서만 일차역학으로 제거된다(Fig. 3).

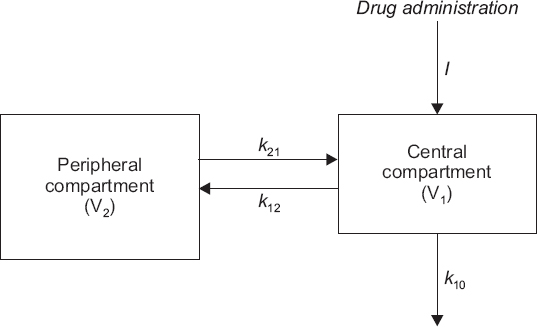Fig. 3

Two compartment mammillary pharmacokinetic model. I: input. k_ij: mirco-rate constant from compartment i to compartment j. V_i: volume of distribution of compartment i. Here, i = 1, 2.

단회정주 때의 혈장농도

먼저 구획별 약물량 변화에 대한 미분방정식은 아래와 같다.

\begin{array}{l} \frac{d A_{1} (t)}{d t} = A_{2} (t) k_{21} - A_{1} (t) (k_{10} + k_{12}) \\ \frac{d A_{2} (t)}{d t} = A_{1} (t) k_{12} - A_{2} (t) k_{21} \end{array}

위 미분방정식을 라플라스 변환하여, A₁(s)와 A₂(s)에 대하여 재정렬하면 다음과 같다.

\begin{array}{l} s A_{1} (s) - A_{1} (0) = A_{2} (s) k_{21} - A_{1} (s) (k_{10} + k_{12}) \\ s A_{2} (s) - A_{2} (0) = A_{1} (s) k_{12} - A_{2} (s) k_{21} \end{array}

A₁(0)=Dose

A₂(0)=Dose

이므로

\begin{array}{l} (s + k_{10} + k_{12}) A_{1} (s) - k_{21} A_{2} (s) = D o s e \\ - k_{12} A_{1} (s) + (s + k_{12}) A_{2} (s) = 0 \end{array}

이다. 전술한 크레머 공식 설명의 x는 위 식의 A₁(s), y는 A₂(s)라고 볼 수 있다.

따라서

\begin{array}{l} D = [\begin{matrix} s + k_{10} + k_{12} & - k_{21} \\ - k_{12} & s + k_{21} \end{matrix}] \\ D_{1} = [\begin{matrix} D o s e & - k_{21} \\ 0 & s + k_{21} \end{matrix}] \\ D_{2} = [\begin{matrix} s + k_{10} + k_{12} & D o s e \\ - k_{12} & 0 \end{matrix}] \end{array}

A_{1} (s) = \frac{| D_{1} |}{| D |} = \frac{D o s e \cdot (s + k_{21})}{(s + k_{10} + k_{12}) (s + k_{21}) - k_{12} k_{21}} = \frac{D o s e \cdot (s + k_{21})}{s^{2} + s (k_{10} + k_{12} + k_{21}) + k_{10} k_{21}}

A_{2} (s) = \frac{| D_{2} |}{| D |} = \frac{D o s e \cdot k_{12}}{(s + k_{10} + k_{12}) (s + k_{21}) - k_{12} k_{21}} = \frac{D o s e \cdot k_{12}}{s^{2} + s (k_{10} + k_{12} + k_{21}) + k_{10} k_{21}}

s^{2} + s (k_{10} + k_{12} + k_{21}) + k_{10} k_{21}

의 해를 −λ₁, −λ₂라고 하면 (s+λ₁)(s+λ₂)가 된다.

따라서 라플라스 영역에서 중심구획의 약물량은 다음과 같다.

A_{1} (s) = \frac{D o s e \cdot (s + k_{21})}{(s + λ_{1}) (s + λ_{2})}

Dose는 단회정주 때 라플라스 영역의 입력함수(input function) 이며,

\frac{(s + k_{21})}{(s + λ_{1}) (s + λ_{2})}

는 이구획 모형에서 중심구획의 배치함수(dis- position function)이다. 따라서, 라플라스 영역의 중심구획 약물량은 입력함수(input function)와 중심구획 배치함수(disposition function)의 곱임을 알 수 있다.

먼저 라플라스 변환표를 이용하여 라플라스 영역의 중심구획 약물량을 시간영역의 식으로 바꿔보자.

\frac{s + α}{(s + a) (s + b)} \to \frac{1}{b - a} [(α - a) \cdot e^{- a \cdot t} - (α - b) \cdot e^{- b \cdot t}]

이므로

\begin{array}{l} \frac{(s + k_{21})}{(s + λ_{1}) (s + λ_{2})} \to \frac{1}{λ_{2} - λ_{1}} [(k_{21} - λ_{1}) \cdot e^{- λ_{1} \cdot t} - (k_{21} - λ_{2}) \cdot e^{- λ_{2} \cdot t}] \\ = \frac{1}{λ_{1} - λ_{2}} [(λ_{1} - k_{21}) \cdot e^{- λ_{1} \cdot t} + (k_{21} - λ_{2}) \cdot e^{- λ_{2} \cdot t}] \end{array}

따라서

A_{1} (t) = D o s e \cdot [\frac{(λ_{1} - k_{21})}{λ_{1} - λ_{2}} \cdot e^{- λ_{1} \cdot t} + \frac{(k_{21} - λ_{2})}{λ_{1} - λ_{2}} \cdot e^{- λ_{2} \cdot t}]

C_{p} (t) = D o s e \cdot [\frac{(λ_{1} - k_{21})}{V_{1} \cdot (λ_{1} - λ_{2})} \cdot e^{- λ_{1} \cdot t} + \frac{(k_{21} - λ_{2})}{V_{1} \cdot (λ_{1} - λ_{2})} \cdot e^{- λ_{2} \cdot t}]

다음은 매트랩을 이용하여 계산해보자.

A_{1} (s) = \frac{D o s e \cdot (s + k_{21})}{(s + λ_{1}) (s + λ_{2})}

을 바로 역라플라스 변환하면 된다.

>> syms s k21 L1 L2 Dose t

>> ilaplace(Dose*(s+k21)/((s+L1)*(s+L2)))

ans = (\exp (- L 2 * t) * (Dose * k 21 - Dose * L 2)) / (L 1 - L 2) - (\exp (- L 1 * t) * (Dose * k 21 - Dose * L 1)) / (L 1 - L 2)

>> simplify(ans)

ans = (Dose * \exp (- L 2 * t) * (L 1 - k 21)) / (L 1 - L 2) - (Dose * \exp (- L2*t) * (L2 - k 21)) / (L 1 - L 2)

따라서

\begin{array}{l} A 1 (t) = D o s e \cdot e^{- λ_{1} \cdot t} \cdot \frac{(λ_{1} - k_{21})}{λ_{1} - λ_{2}} - D o s e \cdot e^{- λ_{2} \cdot t} \cdot \frac{(λ_{2} - k_{21})}{λ_{1} - λ_{2}} \\ = D o s e \cdot [\frac{(λ_{1} - k_{21})}{λ_{1} - λ_{2}} \cdot e^{- λ_{1} \cdot t} + \frac{(k_{21} - λ_{2})}{λ_{1} - λ_{2}} \cdot e^{- λ_{2} \cdot t}] \end{array}

C p (t) = D o s e \cdot [\frac{(λ_{1} - k_{21})}{V_{1} \cdot (λ_{1} - λ_{2})} \cdot e^{- λ_{1} \cdot t} + \frac{(k_{21} - λ_{2})}{V_{2} \cdot (λ_{1} - λ_{2})} \cdot e^{- λ_{2} \cdot t}]

마지막으로 베넷의 일반 부분분수 정리를 이용하여 역라플라스 변환해보자.

A_{1} (s) = \frac{D o s e \cdot (s + k_{21})}{(s + λ_{1}) (s + λ_{2})}

분모의 근은 −λ₁, −λ₂이다.

\begin{array}{l} s = - λ_{1} \\ \frac{D o s e \cdot (- λ_{1} + k_{21})}{(- λ_{1} + λ_{2})} \cdot e^{- λ_{1} \cdot t} = \frac{D o s e \cdot (- λ_{1} + k_{21})}{(λ_{1} - λ_{2})} \cdot e^{- λ_{1} \cdot t} \end{array}

\begin{array}{l} s = - λ_{2} \\ \frac{D o s e \cdot (- λ_{2} + k_{21})}{(- λ_{2} + λ_{1})} \cdot e^{- λ_{2} \cdot t} = \frac{D o s e \cdot (- k_{21} + λ_{2})}{(λ_{1} - λ_{2})} \cdot e^{- λ_{2} \cdot t} \end{array}

A₁(t)는 위에서 계산한 두 식을 더해주면 된다.

\begin{array}{l} A_{1} (t) = \frac{D o s e \cdot (λ_{1} - k_{21})}{λ_{1} - λ_{2}} \cdot e^{- λ_{1} \cdot t} + \frac{D o s e \cdot (k_{21} - λ_{2})}{λ_{1} - λ_{2}} \cdot e^{- λ_{2} \cdot t} \\ = D o s e \cdot [\frac{(λ_{1} - k_{21})}{λ_{1} - λ_{2}} \cdot e^{- λ_{1} \cdot t} + \frac{(k_{21} - λ_{2})}{λ_{1} - λ_{2}} \cdot e^{- λ_{2} \cdot t}] \end{array}

C p (t) = D o s e \cdot [\frac{(λ_{1} - k_{21})}{V_{1} \cdot (λ_{1} - λ_{2})} \cdot e^{- λ_{1} \cdot t} + \frac{(k_{21} - λ_{2})}{V_{1} \cdot (λ_{1} - λ_{2})} \cdot e^{- λ_{2} \cdot t}]

\begin{array}{l} C_{1} = \frac{(λ_{1} - k_{21})}{V_{1} \cdot (λ_{1} - λ_{2})} \\ C_{2} = \frac{(k_{21} - λ_{2})}{V_{1} \cdot (λ_{1} - λ_{2})} \end{array}

이라고 하면

C p (t) = D o s e \cdot (C_{1} \cdot e^{- λ_{1} \cdot t} + C_{2} \cdot e^{- λ_{2} \cdot t}

이구획 모형의 혈장농도 단위약물배치함수는 아래와 같다.

C p (t) = C_{1} \cdot e^{- λ_{1} \cdot t} + C_{2} \cdot e^{- λ_{2} \cdot t}

이 식은 투여방식이나 투여경로에 따라 달라지지 않는다.

Fig. 4에서 보면, 이구획 약동학 모형을 따르는 약물은 단회정주 후 혈중농도 단위약물배치함수의 기울기가 −λ₁, −λ₂임을 알 수 있다.

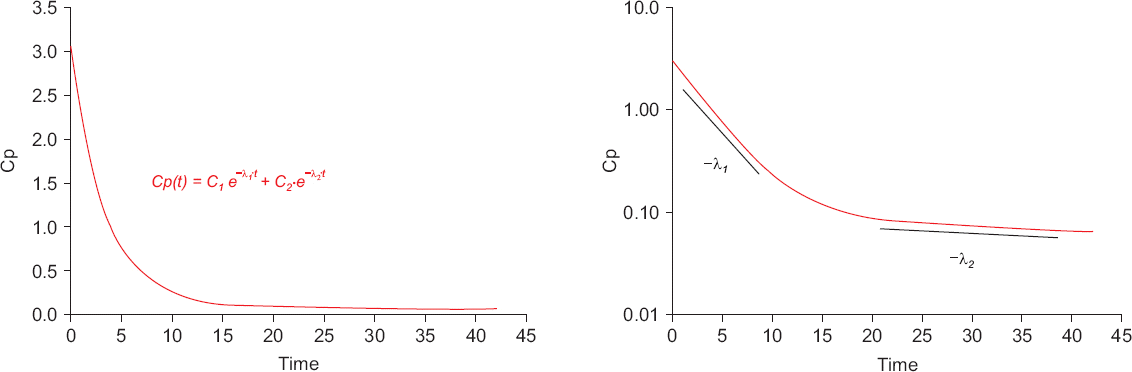Fig. 4

Time-concentration curve after an intravenous bolus of a drug following two compartment pharmacokinetic model with first-order elimination (left panel). The λ₁ and λ₂ are the slopes of distribution and elimination phases in the semi-log graph, respectively (right panel).

영차지속정주 때의 혈장농도

라플라스 영역의 중심구획 약물량은 입력함수(input function)와 중심구획 배치함수(disposition function)의 곱이다. 앞에서, 영차지속정주 때 라플라스 영역의 입력함수는

I n_{s} = \frac{R a t e}{s} \cdot (1 - e^{- S \cdot D U R})

이때 DUR은 infusion duration이다.

영차지속정주나 단회정주 모두 중심구획의 배치함수는 변함없이 아래와 같다.

\frac{(s + k_{21})}{(s + λ_{1}) (s + λ_{2})}

그러므로 라플라스 영역의 중심구획 약물량은 다음과 같다.

\begin{array}{l} A_{1} S = \frac{R a t e}{s} \cdot (1 - e^{- s \cdot D U R}) \cdot \frac{(s + k_{21})}{(s + λ_{1}) (s + λ_{2})} \\ = \frac{R a t e \cdot (1 - e^{- s \cdot D U R}) \cdot (s + k_{21})}{s \cdot (s + λ_{1}) (s + λ_{2})} \end{array}

위 식은 분모가 분자보다 s에 대하여 더 차수가 높고, 분모에 동일인수가 반복되지 않는다. 따라서 역라플라스 변환에 베넷의 일반 부분분수 정리를 적용할 수 있다.

분모의 근은 0, −λ₁, −λ₂이다. 위 식의 모든 s를 이들 근(root)으로 한번씩 치환하고, e^rootㆍt를 곱하여 모두 다 더한다.

0의 경우 분자가 0이 되므로 할 필요가 없다.

−λ₁으로 s를 치환하면

\begin{array}{l} \frac{R a t e \cdot (1 - e^{λ_{1} \cdot D U R}) \cdot (- λ_{1} + k_{21})}{- λ_{1} \cdot (- λ_{1} + λ_{2})} \cdot e^{- λ_{1} \cdot t} \\ = \frac{R a t e \cdot (k_{21} - λ_{1}) \cdot (1 - e^{λ_{1} \cdot D U R})}{λ_{1} \cdot (- λ_{1} - λ_{2})} \cdot e^{- λ_{1} \cdot t} \end{array}

−λ₂로 s를 치환하면

\begin{array}{l} \frac{R a t e \cdot (1 - e^{λ_{2} \cdot D U R}) \cdot (- λ_{2} + k_{21})}{- λ_{2} \cdot (- λ_{2} + λ_{1})} \cdot e^{- λ_{2} \cdot t} \\ = \frac{R a t e \cdot (1 - e^{λ_{2} \cdot D U R}) \cdot (λ_{2} - k_{21})}{λ_{2} \cdot (- λ_{1} - λ_{2})} \cdot e^{- λ_{2} \cdot t} \end{array}

따라서 중심구획 약물량은

A_{1} (t) = \frac{R a t e \cdot (k_{21} - λ_{1}) \cdot (1 - e^{λ_{1} \cdot D U R})}{λ_{1} \cdot (λ_{1} + λ_{2})} \cdot e^{- λ_{1} \cdot t} + \frac{R a t e \cdot (1 - e^{λ_{2} \cdot D U R}) \cdot (λ_{2} - k_{21})}{λ_{2} \cdot (λ_{1} - λ_{2})} \cdot e^{- λ_{2} \cdot t}

혈장농도는 다음과 같다.

C p (t) = \frac{R a t e \cdot (k_{21} - λ_{1}) \cdot (1 - e^{λ_{1} \cdot D U R})}{V_{1} \cdot λ_{1} \cdot (λ_{1} - λ_{2})} \cdot e^{- λ_{1} \cdot t} + \frac{R a t e \cdot (1 - e^{λ_{2} \cdot D U R}) \cdot (λ_{2} - k_{21})}{V_{1} \cdot λ_{2} \cdot (λ_{1} - λ_{2})} \cdot e^{- λ_{2} \cdot t}

영차지속정주 도중이라면 DUR = t

C p (t) = \frac{R a t e \cdot (k_{21} - λ_{1}) \cdot (1 - e^{λ_{1} \cdot t})}{V_{1} \cdot λ_{1} \cdot (λ_{1} - λ_{2})} \cdot e^{- λ_{1} \cdot t} + \frac{R a t e \cdot (1 - e^{λ_{2} \cdot t}) \cdot (λ_{2} - k_{21})}{V_{1} \cdot λ_{2} \cdot (λ_{1} - λ_{2})} \cdot e^{- λ_{2} \cdot t}

\begin{array}{l} = \frac{R a t e \cdot (k_{21} - λ_{1}) \cdot (e^{- λ_{1} \cdot t} - 1)}{V_{1} \cdot λ_{1} \cdot (λ_{1} - λ_{2})} + \frac{R a t e \cdot (e^{- λ_{2} \cdot t} - 1) \cdot (λ_{2} - k_{21})}{V_{1} \cdot λ_{2} \cdot (λ_{1} - λ_{2})} \\ = \frac{R a t e \cdot (λ_{1} - k_{21}) \cdot (1 - e^{- λ_{1} \cdot t})}{V_{1} \cdot λ_{1} \cdot (λ_{1} - λ_{2})} + \frac{R a t e \cdot (1 - e^{- λ_{2} \cdot t}) \cdot (k_{21} - λ_{2})}{V_{1} \cdot λ_{2} \cdot (λ_{1} - λ_{2})} \end{array}

앞에서

\begin{array}{l} C_{1} = \frac{(λ_{1} - k_{21})}{V_{1} \cdot (λ_{1} - λ_{2})} \\ C_{2} = \frac{(k_{21} - λ_{2})}{V_{1} \cdot (λ_{1} - λ_{2})} \end{array}

이므로

C p (t) = \frac{R a t e \cdot C_{1} \cdot (1 - e^{- λ_{1} \cdot t})}{λ_{1}} + \frac{R a t e \cdot C_{2} \cdot (1 - e^{- λ_{2} \cdot t}}{λ_{2}}

영차지속정주 종료 후는 t > DUR

C p (t) = \frac{R a t e \cdot C_{1} \cdot (1 - e^{- λ_{1} \cdot D U R})}{λ_{1}} \cdot e^{- λ_{1} \cdot (t - D U R)} + \frac{R a t e \cdot C_{2} \cdot (1 - e^{- λ_{2} \cdot D U R})}{λ_{2}} \cdot e^{- λ_{2} \cdot (t - D U R)}

이구획 약동학 모형에서 단회정주 후 혈중농도 약물배치함수의 기울기가 −λ₁, −λ₂였음을 기억하라. 영차지속정주 때도 지속정주 종료 이후 혈중농도의 지수함수적 감소의 기울기가 −λ₁, −λ₂이므로, 위 식과 같은 형태를 가진다(Fig. 5). 이 같은 원리는 일구획이나 삼구획 약동학 모형에도 똑같이 적용되며, 전자는 혈중농도 약물배치함수의 기울기가 1개, 후자는 3개인 점이 다를 뿐이다.

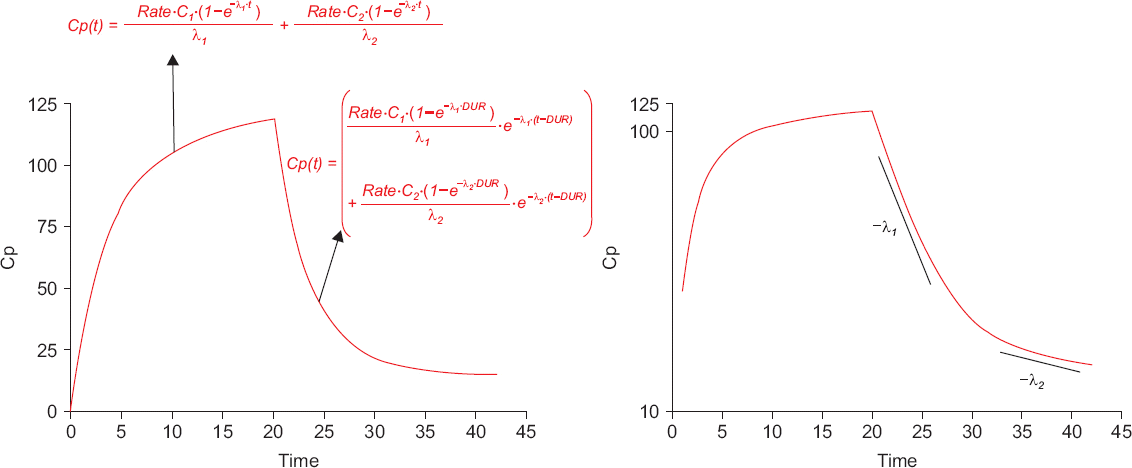Fig. 5

Time-concentration curve after zero-order infusion of a drug following two compartment pharmacokinetic model with first-order elimination. Note that pharmacokinetic equations during and after infusion are different (left panel). Assuming that infusion duration (DUR) is 20 min, plasma concentration reaches its peak at the end of infusion (20 hours). This peak concentration is as follows.

C p (20) = \frac{R a t e \cdot C_{1} \cdot (1 - e^{- λ_{1} \cdot 20})}{λ_{1}} + \frac{R a t e \cdot C_{2} \cdot (1 - e^{- λ_{2} \cdot 20})}{λ_{2}}

Plasma concentration declines after the peak concentration. The λ₁ and λ₂ are the slopes of distribution and elimination phases in the semi-log graph, respectively (right panel). After the end of infusion, the followings are numerical values (DUR = 20 hours).

\frac{R a t e \cdot C_{1} \cdot (1 - e^{- λ_{1} \cdot D U R})}{λ_{1}} + \frac{R a t e \cdot C_{2} \cdot (1 - e^{- λ_{2} \cdot D U R})}{λ_{2}}

이구획 약동학 모형에 효과구획이 추가된 삼구획 모형

모형도식

이구획 약동학 모형의 중심구획에 효과구획이 일차역학으로 연결된다(Fig. 6).

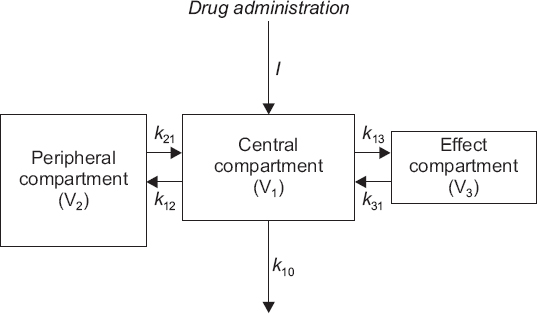Fig. 6

Two compartment mammillary pharmacokinetic model with an effect compartment. I: input. k_ij: mirco-rate constant from compartment i to compartment j. V_i: volume of distribution of compartment i. Here, i = 1, 2, 3.

단회정주

각 구획의 약물량 변화는 다음과 같다. A₁(t), A₃(t)는 각각 중심구획(혈장)과 효과구획의 약물량이다.

\begin{array}{l} \frac{d A_{1} (t)}{d t} = A_{2} (t) k_{21} + A_{3} (t) k_{31} - A_{1} (t) (k_{10} + k_{12} + k_{13}) \\ \frac{d A_{2} (t)}{d t} = A_{1} (t) k_{12} - A_{2} (t) k_{21} \\ \frac{d A_{3} (t)}{d t} = A_{1} (t) k_{13} - A_{3} (t) k_{31} \end{array}

\begin{matrix} s A_{1} (s) - A_{1} (0) = A_{2} (s) k_{21} + A_{3} (s) k_{31} - A_{1} (s) (k_{10} + k_{12} + k_{13}) \\ s A_{2} (s) - A_{2} (0) = A_{1} (s) k_{12} + A_{2} (s) k_{21} \\ s A_{3} (s) - A_{3} (0) = A_{1} (s) k_{13} + A_{3} (s) k_{31} \end{matrix}

\begin{matrix} A_{1} (0) = D o s e \\ A_{2} (0) = 0 \\ A_{3} (0) = 0 \end{matrix}

\begin{array}{l} (s + k_{10} + k_{12} + k_{13}) A_{1} (s) - k_{21} A_{2} (s) - k_{31} A_{3} (s) = D o s e \\ \begin{matrix} - k_{12} A_{1} (s) + (s + k_{21}) A_{2} (s) + 0 \times A_{3} (s) = 0 \\ - k_{13} A_{1} (s) + 0 \times A_{2} (s) + (s + k_{31}) A_{3} (s) = 0 \end{matrix} \end{array}

D = [\begin{matrix} s + k_{10} + k_{12} + k_{13} & - k_{21} & - k_{31} \\ - k_{12} & s + k_{21} & 0 \\ - k_{13} & 0 & s + k_{31} \end{matrix}]

| D | = s^{3} + (k_{10} + k_{12} + k_{13} + k_{21} + k_{31}) s^{2} + (k_{10} k_{21} + k_{13} k_{21} + k_{10} k_{31} + k_{12} k_{31} + k_{21} k_{31}) s + k_{10} k_{21} k_{31}

이 방정식의 근을 −λ₁, −λ₂, −λ₃라고 하면

| D | = (s + λ_{1}) (s + λ_{2}) (s + λ_{3})

한편,

\begin{array}{l} D_{1} = [\begin{matrix} D o s e & - k_{21} & - k_{31} \\ 0 & s + k_{21} & 0 \\ 0 & 0 & s + k_{31} \end{matrix}] \\ | D_{1} | = D o s e \cdot (s + k_{21}) (s + k_{31}) \end{array}

\begin{array}{l} D_{2} = [\begin{matrix} s + k_{10} + k_{12} + k_{13} & D o s e & - k_{31} \\ - k_{12} & 0 & 0 \\ - k_{13} & 0 & s + k_{31} \end{matrix}] \\ | D_{2} | = D o s e \cdot k_{21} \cdot (s + k_{31}) \end{array}

\begin{array}{l} D_{3} = [\begin{matrix} s + k_{10} + k_{12} + k_{13} & - k_{21} & D o s e \\ - k_{12} & s + k_{21} & 0 \\ - k_{13} & 0 & 0 \end{matrix}] \\ | D_{3} | = D o s e \cdot k_{31} \cdot (s + k_{31}) \end{array}

이다.

중심구획

A_{1} (s) = \frac{| D_{1} |}{| D |} = \frac{D o s e \cdot (s + k_{21}) (s + k_{31})}{(s + λ_{1}) (s + λ_{2}) (s + λ_{3})}

베넷의 일반 부분분수 정리를 적용하여 중심구획 약물량과 혈장농도를 계산하면 다음과 같다. 한번 해보기 바란다.

A_{1} (t) = D o s e \cdot (\frac{(λ_{1} - k_{21}) (λ_{1} - k_{31})}{(λ_{1} - λ_{2}) (λ_{1} - λ_{3})} \cdot e^{- λ_{1} \cdot t} - \frac{(λ_{2} - k_{21}) (λ_{2} - k_{31})}{(λ_{1} - λ_{2}) (λ_{2} - λ_{3})} \cdot e^{- λ_{2} \cdot t} + \frac{(λ_{3} - k_{21}) (λ_{3} - k_{31})}{(λ_{1} - λ_{3}) (λ_{2} - λ_{3})} \cdot e^{- λ_{3} \cdot t})

C p (t) = D o s e \cdot (\frac{(λ_{1} - k_{21}) (λ_{1} - k_{31})}{V_{1} \cdot (λ_{1} - λ_{2}) (λ_{1} - λ_{3})} \cdot e^{- λ_{1} \cdot t} - \frac{(λ_{2} - k_{21}) (λ_{2} - k_{31})}{V_{1} \cdot (λ_{1} - λ_{2}) (λ_{2} - λ_{3})} \cdot e^{- λ_{2} \cdot t} + \frac{(λ_{3} - k_{21}) (λ_{3} - k_{31})}{V_{1} \cdot (λ_{1} - λ_{3}) (λ_{2} - λ_{3})} \cdot e^{- λ_{3} \cdot t})

\begin{array}{l} C_{1} = \frac{(λ_{1} - k_{21}) (λ_{1} - k_{31})}{V_{1} \cdot (λ_{1} - λ_{2}) (λ_{1} - λ_{3})} \\ C_{2} = \frac{(λ_{2} - k_{21}) (λ_{2} - k_{31})}{V_{1} \cdot (λ_{1} - λ_{2}) (λ_{2} - λ_{3})} \\ C_{3} = \frac{(λ_{3} - k_{21}) (λ_{3} - k_{31})}{V_{1} \cdot (λ_{1} - λ_{2}) (λ_{2} - λ_{3})} \end{array}

이라고 하면,

C p (t) = D o s e \cdot (C_{1} \cdot e^{- λ_{1} \cdot t} + C_{2} \cdot e^{- λ_{2} \cdot t} + C_{3} \cdot e^{- λ_{3} \cdot t})

아래 식이 삼구획 모형의 혈장농도 단위약물배치함수이다(투여방식이나 투여경로에 따라서 달라지지 않음).

C p (t) = C_{1} \cdot e^{- λ_{1} \cdot t} + C_{2} \cdot e^{- λ_{2} \cdot t} + C_{3} \cdot e^{- λ_{3} \cdot t}

효과구획

A_{3} (s) = \frac{| D_{3} |}{| D |} = \frac{D o s e \cdot k_{13} \cdot (s + k_{21})}{(s + λ_{1}) (s + λ_{2}) (s + λ_{3})}

마찬가지로, 베넷의 일반 부분분수 정리를 적용하여 효과구획 약물량과 효과처 농도를 계산하면 다음과 같다.

A_{3} (t) = D o s e \cdot [- \frac{k_{13} \cdot (λ_{1} - k_{21})}{(λ_{1} - λ_{2}) (λ_{1} - λ_{3})} \cdot e^{- λ_{1} \cdot t} + \frac{k_{13} \cdot (λ_{2} - k_{21})}{(λ_{1} - λ_{2}) (λ_{2} - λ_{3})} \cdot e^{- λ_{2} \cdot t} - \frac{k_{13} \cdot (λ_{3} - k_{21})}{(λ_{1} - λ_{2}) (λ_{2} - λ_{3})} \cdot e^{- λ_{3} \cdot t}]

C e (t) = D o s e \cdot [\frac{k_{13} \cdot (k_{21} - λ_{1})}{V_{3} \cdot (λ_{1} - λ_{2}) (λ_{1} - λ_{3})} \cdot e^{- λ_{1} \cdot t} + \frac{k_{13} \cdot (k_{21} - λ_{2})}{V_{3} \cdot (λ_{1} - λ_{2}) (λ_{2} - λ_{3})} \cdot e^{- λ_{2} \cdot t} - \frac{k_{13} \cdot (k_{21} - λ_{3})}{V_{3} \cdot (λ_{1} - λ_{2}) (λ_{2} - λ_{3})} \cdot e^{- λ_{3} \cdot t}]

\begin{array}{l} V_{1} k_{13} = V_{3} k_{31} \\ \frac{k_{13}}{V_{3}} = \frac{k_{13}}{V_{1}} \end{array}

C e (t) = D o s e \cdot [\frac{k_{31} \cdot (k_{21} - λ_{1})}{V_{1} \cdot (λ_{1} - λ_{2}) (λ_{1} - λ_{3})} \cdot e^{- λ_{1} \cdot t} + \frac{k_{31} \cdot (k_{21} - λ_{2})}{V_{1} \cdot (λ_{1} - λ_{2}) (λ_{2} - λ_{3})} \cdot e^{- λ_{2} \cdot t} - \frac{k_{31} \cdot (k_{21} - λ_{3})}{V_{1} \cdot (λ_{1} - λ_{3}) (λ_{2} - λ_{3})} \cdot e^{- λ_{3} \cdot t}]

앞에서 다음과 같았음을 기억하라.

\begin{array}{l} C_{1} = \frac{(λ_{1} - k_{21}) (λ_{1} - k_{31})}{V_{1} \cdot (λ_{1} - λ_{2}) (λ_{1} - λ_{3})} \\ C_{2} = \frac{(λ_{2} - k_{21}) (λ_{2} - k_{31})}{V_{1} \cdot (λ_{1} - λ_{2}) (λ_{2} - λ_{3})} \\ C_{3} = \frac{(λ_{3} - k_{21}) (λ_{3} - k_{31})}{V_{1} \cdot (λ_{1} - λ_{2}) (λ_{2} - λ_{3})} \end{array}

따라서,

\begin{array}{l} \frac{k_{21} - λ_{1}}{V_{1} \cdot (λ_{1} - λ_{2}) (λ_{1} - λ_{3})} = \frac{C_{1}}{k_{31} - λ_{1}} \\ \frac{k_{21} - λ_{2}}{V_{1} \cdot (λ_{1} - λ_{2}) (λ_{2} - λ_{3})} = \frac{C_{2}}{k_{31} - λ_{2}} \\ \frac{k_{21} - λ_{3}}{V_{1} \cdot (λ_{1} - λ_{3}) (λ_{2} - λ_{3})} = \frac{C_{1}}{k_{31} - λ_{3}} \end{array}

C e (t) = D o s e \cdot [\frac{k_{31}}{k_{31} - λ_{1}} \cdot C_{1} \cdot e^{- λ_{1} \cdot t} + \frac{k_{31}}{k_{31} - λ_{2}} \cdot C_{2} \cdot e^{- λ_{2} \cdot t} + \frac{k_{31}}{k_{31} - λ_{3}} \cdot C_{3} \cdot e^{- λ_{3} \cdot t}]

영차지속정주

중심구획

라플라스 영역의 입력함수는 다음과 같았다.

I n_{s} = \frac{R a t e}{s} \cdot (1 - e^{- s \cdot D U R})

단회정주 때 중심구획 약물량은 다음과 같았다.

A_{1} (s) = \frac{D o s e \cdot (s + k_{21}) (s + k_{31})}{(s + λ_{1}) (s + λ_{2}) (s + λ_{3})}

따라서 중심구획 배치함수는 다음과 같을 것이다.

\frac{(s + k_{21}) (S + k_{31})}{(s + λ_{1}) (s + λ_{2}) (s + λ_{3})}

그러므로 영차지속정주 때 중심구획 약물량은 입력함수와 중심구획 배치함수의 곱이므로 다음과 같다.

\begin{array}{l} A_{1} (s) = \frac{R a t e}{s} \cdot (1 - e^{- s \cdot D U R}) \cdot \frac{(s + k_{21}) (s + k_{31})}{(s + λ_{1}) (s + λ_{2}) (s + λ_{3})} \\ A_{1} (s) = Rate \cdot \frac{(s + k_{21}) (s + k_{31})}{s \cdot (s + λ_{1}) (s + λ_{2}) (s + λ_{3})} \cdot (1 - e^{- s \cdot D U R}) \end{array}

베넷의 일반 부분분수 정리를 이용하여 역라플라스 변환을 하면(분모의 근은 0, −λ₁, −λ₂, −λ₃이다),

\begin{array}{l} A_{1} (t) = R a t e \cdot \frac{(k_{21} - λ_{1}) (k_{31} - λ_{1})}{λ_{1} \cdot (λ_{1} - λ_{2}) (λ_{3} - λ_{1})} \cdot (1 - e^{λ_{1} \cdot D U R}) \cdot e^{- λ_{1} \cdot t} \\ + R a t e \cdot \frac{(k_{21} - λ_{2}) (k_{31} - λ_{2})}{λ_{2} \cdot (λ_{2} - λ_{1}) (λ_{3} - λ_{2})} \cdot (1 - e^{λ_{2} \cdot D U R}) \cdot e^{- λ_{2} \cdot t} \\ + R a t e \cdot \frac{(k_{21} - λ_{3}) (k_{31} - λ_{3})}{λ_{3} \cdot (λ_{3} - λ_{1}) (λ_{2} - λ_{3})} \cdot (1 - e^{λ_{3} \cdot D U R}) \cdot e^{- λ_{3} \cdot t} \end{array}

\begin{array}{l} C p (t) = R a t e \cdot \frac{(k_{21} - λ_{1}) (k_{31} - λ_{1})}{V_{1} \cdot λ_{1} \cdot (λ_{1} - λ_{2}) (λ_{3} - λ_{1})} \cdot (1 - e^{λ_{1} \cdot D U R}) \cdot e^{- λ_{1} \cdot t} \\ + R a t e \cdot \frac{(k_{21} - λ_{2}) (k_{31} - λ_{2})}{V_{1} \cdot λ_{2} \cdot (λ_{2} - λ_{1}) (λ_{3} - λ_{2})} \cdot (1 - e^{λ_{2} \cdot D U R}) \cdot e^{- λ_{2} \cdot t} \\ + R a t e \cdot \frac{(k_{21} - λ_{3}) (k_{31} - λ_{3})}{V_{1} \cdot λ_{3} \cdot (λ_{3} - λ_{1}) (λ_{2} - λ_{3})} \cdot (1 - e^{λ_{3} \cdot D U R}) \cdot e^{- λ_{3} \cdot t} \end{array}

영차지속정주 동안이라면 DUR = t

C p (t) = R a t e \cdot [\begin{array}{l} \frac{(k_{21} - λ_{1}) (k_{31} - λ_{1})}{V_{1} \cdot λ_{1} \cdot (λ_{1} - λ_{2}) (λ_{1} - λ_{3})} \cdot (1 - e^{- λ_{1} \cdot t}) \\ \frac{(k_{21} - λ_{2}) (k_{31} - λ_{2})}{V_{1} \cdot λ_{2} \cdot (λ_{2} - λ_{1}) (λ_{2} - λ_{3})} \cdot (1 - e^{- λ_{2} \cdot t}) \\ \frac{(k_{21} - λ_{3}) (k_{31} - λ_{3})}{V_{1} \cdot λ_{3} \cdot (λ_{3} - λ_{1}) (λ_{3} - λ_{2})} \cdot (1 - e^{- λ_{3} \cdot t}) \end{array}]

영차지속정주 종료 후는 t > DUR

\begin{array}{l} C p (t) = R a t e \cdot \frac{(k_{21} - λ_{1}) (k_{31} - λ_{1})}{V_{1} \cdot λ_{1} \cdot (λ_{1} - λ_{2}) (λ_{1} - λ_{3})} \cdot (1 - e^{- λ_{1} \cdot D U R}) \cdot e^{- λ_{1} \cdot (t - D U R)} \\ + R a t e \cdot \frac{(k_{21} - λ_{2}) (k_{31} - λ_{2})}{V_{1} \cdot λ_{2} \cdot (λ_{2} - λ_{1}) (λ_{2} - λ_{3})} \cdot (1 - e^{- λ_{2} \cdot D U R}) \cdot e^{- λ_{2} \cdot (t - D U R)} \\ + R a t e \frac{(k_{21} - λ_{3}) (k_{31} - λ_{3})}{V_{1} \cdot λ_{3} \cdot (λ_{3} - λ_{1}) (λ_{3} - λ_{2})} \cdot (1 - e^{- λ_{3} \cdot D U R}) \cdot e^{- λ_{3} \cdot (t - D U R)} \end{array}

효과구획

단회정주 때 효과구획 약물량은 다음과 같았다.

A_{3} (s) = \frac{D o s e \cdot k_{13} \cdot (s + k_{21})}{(s + λ_{1}) (s + λ_{2}) (s + λ_{3})}

따라서 효과구획 배치함수는 다음과 같다.

\frac{k_{13} \cdot (s + k_{21})}{(s + λ_{1}) (s + λ_{2}) (s + λ_{3})}

영차지속정주 때 효과구획 약물량은 입력함수와 효과구획 배치함수의 곱이다.

\begin{array}{l} A_{3} (s) = \frac{R a t e}{s} \cdot (1 - e^{- s . D U R}) \cdot \frac{k_{13} \cdot (s + k_{21})}{(s + λ_{1}) (s + λ_{2}) (s + λ_{3})} \\ A_{3} (s) = \frac{R a t e}{s} \cdot \frac{k_{13} \cdot (s + k_{21})}{S \cdot (s + λ_{1}) (s + λ_{2}) (s + λ_{3})} \cdot (1 - e^{- s . D U R}) \end{array}

베넷의 일반 부분분수 정리를 이용하여 역라플라스 변환을 하면(분모의 근은 0, −λ₁, −λ₂, −λ₃이다),

A_{3} (t) = R a t e \cdot [\begin{array}{l} \frac{k_{13} \cdot (k_{21} - λ_{1})}{- λ_{1} \cdot (λ_{2} - λ_{1}) (λ_{3} - λ_{1})} \cdot (1 - e^{λ_{1} \cdot D U R}) \cdot e^{- λ_{1} \cdot t} \\ + \frac{k_{13} \cdot (k_{21} - λ_{2})}{- λ_{2} \cdot (λ_{1} - λ_{2}) (λ_{3} - λ_{2})} \cdot (1 - e^{λ_{2} \cdot D U R}) \cdot e^{- λ_{2} \cdot t} \\ + \frac{k_{13} \cdot (k_{21} - λ_{3})}{- λ_{3} \cdot (λ_{1} - λ_{3}) (λ_{2} - λ_{3})} \cdot (1 - e^{λ_{3} \cdot D U R}) \cdot e^{- λ_{3} \cdot t} \end{array}]

C e (t) = R a t e \cdot [\begin{array}{l} \frac{k_{13} \cdot (k_{21} - λ_{1})}{V_{3} \cdot - λ_{1} \cdot (λ_{2} - λ_{1}) (λ_{3} - λ_{1})} \cdot (1 - e^{λ_{1} \cdot D U R}) \cdot e^{- λ_{1} \cdot t} \\ + \frac{k_{13} \cdot (k_{21} - λ_{2})}{- V_{3} \cdot λ_{2} \cdot (λ_{1} - λ_{2}) (λ_{3} - λ_{2})} \cdot (1 - e^{λ_{2} \cdot D U R}) \cdot e^{- λ_{2} \cdot t} \\ + \frac{k_{13} \cdot (k_{21} - λ_{3})}{- V_{3} \cdot λ_{3} \cdot (λ_{1} - λ_{3}) (λ_{2} - λ_{3})} \cdot (1 - e^{λ_{3} \cdot D U R}) \cdot e^{- λ_{3} \cdot t} \end{array}]

영차지속정주 동안이라면 DUR = t

C e (t) = R a t e \cdot [\begin{array}{l} \frac{k_{13} \cdot (k_{21} - λ_{1})}{- V_{3} \cdot λ_{1} \cdot (λ_{2} - λ_{1}) (λ_{3} - λ_{1})} \cdot (1 - e^{λ_{1} \cdot t}) \cdot e^{- λ_{1} \cdot t} \\ + \frac{k_{13} \cdot (k_{21} - λ_{2})}{- V_{3} \cdot λ_{2} \cdot (λ_{1} - λ_{2}) (λ_{3} - λ_{2})} \cdot (1 - e^{λ_{2} \cdot t}) \cdot e^{- λ_{2} \cdot t} \\ + \frac{k_{13} \cdot (k_{21} - λ_{3})}{- V_{3} \cdot λ_{3} \cdot (λ_{1} - λ_{3}) (λ_{2} - λ_{3})} \cdot (1 - e^{λ_{3} \cdot t}) \cdot e^{- λ_{3} \cdot t} \end{array}]

\begin{array}{l} V_{1} k_{13} = V_{3} k_{31} \\ \frac{k_{13}}{V_{3}} = \frac{k_{31}}{V_{1}} \end{array}

C e (t) = R a t e \cdot [\begin{array}{l} \frac{k_{31} \cdot (k_{21} - λ_{1})}{V_{1} \cdot λ_{1} \cdot (λ_{2} - λ_{1}) (λ_{3} - λ_{1})} \cdot (1 - e^{- λ_{1} \cdot t}) \\ + \frac{k_{31} \cdot (k_{21} - λ_{2})}{V_{1} \cdot λ_{2} \cdot (λ_{1} - λ_{2}) (λ_{3} - λ_{2})} \cdot (1 - e^{- λ_{2} \cdot t}) \\ + \frac{k_{31} \cdot (k_{21} - λ_{3})}{V_{1} \cdot λ_{3} \cdot (λ_{1} - λ_{3}) (λ_{2} - λ_{3})} \cdot (1 - e^{- λ_{3} \cdot t}) \end{array}]

영차지속정주 종료 후는 t > DUR

C e (t) = R a t e \cdot [\begin{array}{l} \frac{k_{31} \cdot (k_{21} - λ_{1})}{V_{1} \cdot λ_{1} \cdot (λ_{2} - λ_{1}) (λ_{3} - λ_{1})} \cdot (1 - e^{- λ_{1} \cdot D U R}) \cdot e^{- λ_{1} \cdot (t - D U R)} \\ + \frac{k_{31} \cdot (k_{21} - λ_{2})}{V_{1} \cdot λ_{2} \cdot (λ_{1} - λ_{2}) (λ_{3} - λ_{2})} \cdot (1 - e^{- λ_{2} \cdot D U R}) \cdot e^{- λ_{2} \cdot (t - D U R)} \\ + \frac{k_{31} \cdot (k_{21} - λ_{3})}{V_{1} \cdot λ_{3} \cdot (λ_{1} - λ_{3}) (λ_{2} - λ_{3})} \cdot (1 - e^{- λ_{3} \cdot D U R}) \cdot e^{- λ_{3} \cdot (t - D U R)} \end{array}]

결론

이상에서 이구획 약동학 모형에 효과구획이 없는 경우와 있는 경우의 수식을 자세하게 유도해 보았다. 여기서 몇 가지 가정은 1) 중심구획과 말초구획이 일차역학으로 연결되고, 2) 약물은 중심구획에서만 제거되며, 3) 효과구획은 중심구획에 일차역학으로 연결된다는 것이었다. 기타의 수많은 다른 모형들은 기술하지 않았다.

위의 가정을 바탕으로 구획별 약물량 변화에 대한 미분방정식을 세우고, 이를 라플라스 변환, 역라플라스 변환하여 구획별 약물량 함수를 유도하였다. 약물의 투여경로나 투여방법에 따라서 시간, 농도곡선이 다르기 때문에, 이를 기술하는 구획별 약물량 함수 또한 달라야 함을 이해하였을 것이다.

약동학의 주목적은 농도를 예측하는 데 있다. 이를 위하여 약물마다 약동학 모수 추정값을 알아야 한다. 임상시험에서 약물의 투여경로나 투여방법을 정한 다음, 시간 농도자료를 얻는다. 이 자료를 비선형 회귀분석하여 약동학 모수 추정값을 구하는데, 본문에서 유도한 약동학 수식을 회귀분석의 모형 식(model formulation)으로 사용한다. 회귀분석의 모형 식 안에 우리가 구하고자 하는 약동학 모수가 포함되어 있다. 투여 경로나 투여 방법마다 약동학 수식이 다르므로 적절한 것을 선택하여야 할 것이다.

마취통증의학과에서 사용하는 목표농도조절주입은 약동학을 매우 특수하게 이용하는데, 농도 예측이라는 일반적인 목적보다는 특정 농도를 유지하는데 필요한 투여량을 지속적으로 구한다. 목표농도로 혈중농도를 사용할 수 있고, 효과구획 농도도 사용할 수 있는데, 투여량을 계산하려면, 약동학 모수 추정값은 물론이고, 중심구획이나 효과구획의 약물량 함수를 알아야 한다. 전자는 약동약력 모형화를 통하여 추정할 수 있고, 후자는 본문에서 유도하였다.

결론적으로, 약동학 수식에 대한 이해는 마취 및 통증에 사용되는 약물의 최적 용량을 선택할 수 있는 시발점이 된다. 추후 비선형 혼합효과모형(nonlinear mixed effects model)을 이용한 집단 약동약력 분석(population pharmacokinetic and pharmacodynamic analysis)에 이 수식을 응용하면 약동학 모수 추정값을 구할 수 있게 되며, 이것이 바로 약동학 모형이다. 일반적으로 모형은 약물의 농도 예측에 사용되며, 마취통증의학과에서는 목표농도조절주입에도 사용한다. 전자는 임상약리학자(clinical pharmacologist)의 주 관심사이며 신약개발(drug development)이나 임상의학 모두에서 사용할 수 있다. 마취통증의학과 의사가 계량약리를 배운다면, 이러한 일 이외에 목표농도조절주입에도 전문가가 되는 것이라고 볼 수 있다.

약동학 수식유도