PDF
Citation
Print
서론
무작위화(randomization)라는 용어는 특정한 패턴이나 규칙성이 없도록 무엇인가를 만드는 모든 과정을 가리키며, 모집단에서 표본을 추출하는데 이용되는 무작위 추출(random sampling), 무작위 수를 생성하는 난수 생성(random number generation), 무작위 배정 임상 연구(randomized clinical trials)에서 각 치료군(대조군과 시험군)에 약제나 처치를 할당하는데 사용되는 무작위 배정(random allocation)과 같이 다양한 영역에서 사용되고 있다.
무작위화(randomization) 기법은 1920년대에 Ronald A. Fisher에 의해 처음으로 개념화되었으며[1], 이 개념은 1931년 결핵 연구에서 최초로 임상시험에 소개되었다[2]. 무작위화에 기반을 둔 추론(randomization-based inference)은 통계학적 추론에 있어 핵심 원리이며, 연구디자인(experimental design)에서는 무작위 배정(random allocation)으로, 설문조사(survey)에서는 무작위 추출(random sampling)의 형태로 나타난다.
많은 사람이 무작위 추출(random sampling)과 무작위 배정(random allocation)을 혼동하여 사용하고 있지만, 실제 이 둘은 완전히 다르다. 무작위 추출의 목표는 모집단에서 얻어진 작은 크기의 표본집단이 모집단을 대표할 수 있도록 표본 추출하는 것인 반면, 무작위 배정의 목표는 모든 피험자가 각 치료군에 배정될 기회를 같게 만드는 것이기 때문이다.
모든 연구자는 훌륭한 연구를 수행하기 원한다. 이를 위해서는 연구 중에 생길 수 있는 가변성(variability)을 최소화하고 연구자가 연구하고자 하는 요인(본 문헌에서는 ‘치료’라고 하겠다) 이외의 예후 요인(prognostic factor)이 미치는 영향을 피하여 치료가 가지는 효과에 대한 평가를 편향(bias) 없이 내릴 수 있어야 한다. 무작위 배정은 피험자를 치료군에 배정하는 기준을 없애고 연구자의 주관에 의한 배정을 배제한다. 그 결과, 피험자가 각 치료군에 배정될 확률이 동일하도록 하여 치료 이외의 요인에 의해 체계적 방식으로 차이가 발생할 가능성을 최소화한다. 즉, 무작위 배정은 각 피험자에게 치료를 받을 기회를 동등하게 부여하고, 치료를 제외한 모든 예후 요인들을 유사하게 만들어 보다 의미 있는 연구를 수행하고자 하는 노력의 일환인 것이다[3,4].
무작위 배정을 시행하면 이미 알려진 예후 요인뿐만 아니라, 알려지지 않은(우리가 미처 생각하지 못했던) 예후 요인들까지 각 군에 비슷하게 배정할 수 있다. 따라서, 연구자가 피험자를 임의로 배정하여 발생할 수 있는 선택 편향(selection bias)를 제거하고, 예후 요인을 비슷하게 배정하여 교란 편향(confounding bias)의 가능성도 줄인다. 그 결과 연구 종료 후 군 간에 차이가 관찰되면, 군 배정의 차이에 의해 그런 차이가 생겼다고 주장할 수 있는 근거가 된다. 또한, 대부분의 통계 기법이 확률론에 기반을 두고 있으므로 통계적 검정에 대한 근거를 제공한다[5,6].
무작위 배정은 크게 세 가지의 과정으로 구성되는데 각 과정은 1) 배정 순서 생성(random sequence generation), 2) 할당 은닉(allocation concealment) 그리고 3) 실행(commencement)이다[3].
본 문헌에서는 무작위화(randomization) 방법 중 무작위 배정(random allocation)만을, 무작위 배정의 세 과정 중에서 배정순서생성(random sequence generation)만을 살펴볼 것이다. 배정 순서 생성의 종류와 시행 방법들을 예와 함께 설명할 것이며, 각 방법이 가지는 장점 및 단점에 대하여 기술할 것이다. 마지막으로 널리 사용되는 상용 프로그램인 Microsoft Excel 2010 (Microsoft Inc., USA)을 이용하여 단순 및 블록 무작위 배정을 시행하는 간단한 예도 제시하겠다.
본 문
무작위 배정 임상연구는 환자에게 도움이 될 수 있는 치료를 찾기 위한 최선의 방법으로 알려져 있다[4]. 이는 무작위 배정 임상연구에서 시행되는 무작위 배정이 군 간의 비교가능성을 보장하고 통계적 검정에 타당성을 부여하기 때문이다[6].
어떤 진통제의 효과를 시험하는 연구를 한다고 생각해 보자. 이 연구에서 시험군에 배정된 피험자는 새로 개발된 진통제로 치료받고, 대조군에 배정된 피험자는 위약(placebo)으로 치료받는다. 여기에서 나이가 많은 피험자는 통증을 더 잘 참을 수 있어 통증에 대한 시각통증점수(visual analogue scale)를 적게 보고하는 경향이 있다고 하자. 만일 시험군에 나이가 많은 피험자들이 배정된다고 하면, 군 간의 나이 불균형은 연구 결과에 영향을 줄 것이며, 진통제의 실제 약효보다 효과가 크게 나타날 수 있다. 나이라는 예후 요인의 불균형으로 인해 이 연구 결과로는 진통제의 실제 효과와 공변량(예후 요인)에 의한 효과를 구분하기 어려울 것이다.
이럴 경우 연구자들은 연구 결과에서 예후 요인에 의해 생기는 영향을 없애고 실제 효과를 알기 위해 임상 연구의 분석단계에서 공변량의 불균형을 보정한 통계 기법을 사용하기도 한다. 이러한 통계 기법으로는 공분산분석(analysis of covariance, ANCOVA) 혹은 다변량 공분산분석(multivariate ANCOVA, MANCOVA) 등이 있으며, 실제로 많은 연구에서 사용된다. 이런 통계 기법들은 다양한 통계적 가정을 충족시켜야 하지만 실제로는 충족시키지 못하는 경우도 많다. ANCOVA나 MANCOVA에서 중요한 가정 중 하나는 각 공변량에서 회귀직선의 기울기가 동일하다는 것이다. 이 가정에 기반하여 전체 공변량의 회귀 직선의 평균 기울기를 결과 변수의 보정에 사용하기 때문에, 만일 각 공변량의 회귀 직선의 기울기가 다르다면 결과의 해석이 어려울 수 있다[7]. 이처럼, 공변량의 차이에 대처하는 이상적인 방법은 데이터를 모은 후 다양한 통계 기법을 적용하여 해석하기보다는, 연구를 설계하는 단계에서 공변량의 불균형이 발생할 가능성을 줄이는 것이라고 할 수 있다. 이를 위하여 무작위 배정을 적용한다.
무작위 배정의 종류 (TYPES OF RANDOMIZATION)
임상연구에서 무작위 배정을 시행하기 위한 많은 방법이 제안되고 사용되고 있다. 본 문헌에서는 배정확률이 일정한 무작위 배정(fixed allocation randomization)과 배정확률에 변화를 주는 무작위 배정(dynamic allocation randomization, adaptive randomization)으로 나누어 기술하겠다(Table 1).
Table 1
Types of Randomization
연구자는 다양한 무작위 배정의 장단점, 특징들을 이해하여 실제 연구에 적용하고 활용하며, 자료 수집이 끝난 후 해석하고, 타당한 결과를 도출하는 방법을 선택할 수 있어야 한다.
배정확률이 일정한 무작위 배정(Fixed allocation randomization)
배정확률이 일정한 무작위 배정에서는 사전에 정의된 확률로 피험자를 치료군에 배정하며, 이 확률은 바뀌지 않는다. 여기에는 단순 무작위 배정(simple randomization), 블록 무작위 배정(blocked randomization), 층화 무작위 배정(stratified randomization) 등이 있다. 각 치료군에 배정될 배정확률을 같게 하는 것(1：1, 1：1：1 등)이 일반적이나, 대조군보다 시험군에 대한 정보가 많이 필요하거나(예. 독성, 부작용 연구), 대조군보다 시험군의 효과가 뛰어나다는 것이 이미 인정된 경우, 예산이 부족한 경우 등에서는 각 치료군에 배정될 확률을 달리할 수 있다.
1. 단순 무작위 배정(Simple randomization)
피험자를 단일한 일련의 순서(random sequence)에 기반하여 각 치료군에 무작위 배정하는 것을 단순 무작위 배정이라고 하며, 피험자를 각 치료군에 배정하는데 완전한 무작위성(randomness)을 유지할 수 있다[8].
단순 무작위 배정에 있어 가장 이해하기 쉽고 흔히 예로 드는 기본적인 방법은 Ronald A. Fisher가 최초로 제시한 동전던지기 방법이다[1]. 이 방법에서는 던져진 동전이 앞면인지 뒷면인지에 따라 피험자의 치료군 배정을 결정한다. 동전의 앞면과 뒷면이 나올 확률이 각각 50%이므로, 각 치료군에 배정될 확률 또한 50%가 된다. 단순 무작위 배정을 위한 다른 방법으로는 카드를 이용한 방법(홀수-치료군, 짝수-대조군), 주사위 던지기 방법(3 이하-치료군, 4 이상-대조군) 등이 있다. 무작위 배정은 재현이 가능해야 하는데, 이 방법들은 재현할 수 없으므로, 여러 책에 나와 있는 난수표를 이용하거나 다양한 컴퓨터 프로그램을 이용하기도 한다(하지만 많은 컴퓨터 프로그램에서도 재현할 수 없는 경우가 많다).
단순 무작위 배정은 단순하고 구현이 용이하며 이해하기 쉽다는 장점이 있지만, 실제 구현을 하게 되면 각 치료군에 배정되는 피험자 수에 불균형이 생길 수 있다는 문제점이 있다.
표본 수가 많은 연구에서는 대개 각 치료군 간 피험자 수의 차이가 전체 피험자 수에 비추어 무시할 수 있을 정도로 작아 전반적으로 용인될 수 있지만, 표본 수가 적은 연구에서는 불균형의 상대적 크기와 불균형이 발생할 가능성이 커지게 된다. 예를 들어, 시험군과 대조군에 단순무작위 배정을 시행하는 연구에서 시험군과 대조군에 배정된 피험자의 불균형이 20% (60%:40%) 이상 차이가 날 가능성이 총 피험자수가 20명이라면 50%에 이르지만, 100명이라면 5%에 불과하다.
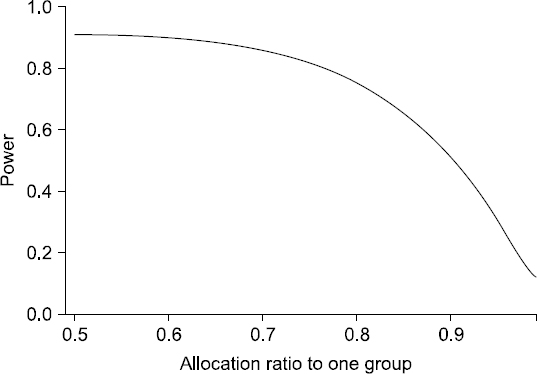
피험자 수의 불균형이 심할 경우 다른 연구자나 독자, 저널의 심사위원, 편집자들이 납득하기 어려울 것이며, 연구의 검정력(power) 또한 낮아진다. 검정력(모집단에서 귀무 가설이 거짓일 경우 표본을 이용한 의사결정과정에서 귀무 가설을 기각할 확률)은 각 치료군에 배정된 피험자 수가 같을 때 가장 높으며, 불균형의 정도가 커질수록 검정력은 낮아진다. 예를 두 군의 평균이 각각 30과 20이고 공동표준편차가 15인 총 100명의 피험자를 대상으로 한 연구에서, 두 군에 배정된 피험자 수가 같을 때(allocation ratio to one group = 0.5)의 검정력은 0.91이나, 1：2로 배정될 경우(allocation ratio to one group = 0.67)는 0.87, 1：4로 배정될 경우(allocation ratio to one group = 0.8)는 0.75로 감소한다(Fig. 1).
따라서 일반적으로 단순 무작위 배정은 피험자의 수가 200명이 넘는 연구에서 권장된다[9].
2. 블록 무작위 배정(Blocked randomization, Permuted- block randomization)
블록 무작위 배정은 단순 무작위 배정에서 발생할 수 있는 군간 피험자수의 불균형을 막기 위하여 설계된 방법이다. 이 방법에서는 연구자가 블록 크기(블록 내에 배정되는 피험자 수)와 배정비(allocation ratio, 각 치료군에 배정되는 피험자 수의 비)를 미리 정해야 한다[10].
블록 크기는 치료군 수의 배수로 정하며(예를 들어 치료군이 2개일 경우 블록의 크기는 4, 6, 8), 블록 크기는 치료군 간 균형의 제어가 용이하도록 되도록 작게 유지하는 것이 이상적이다[9].
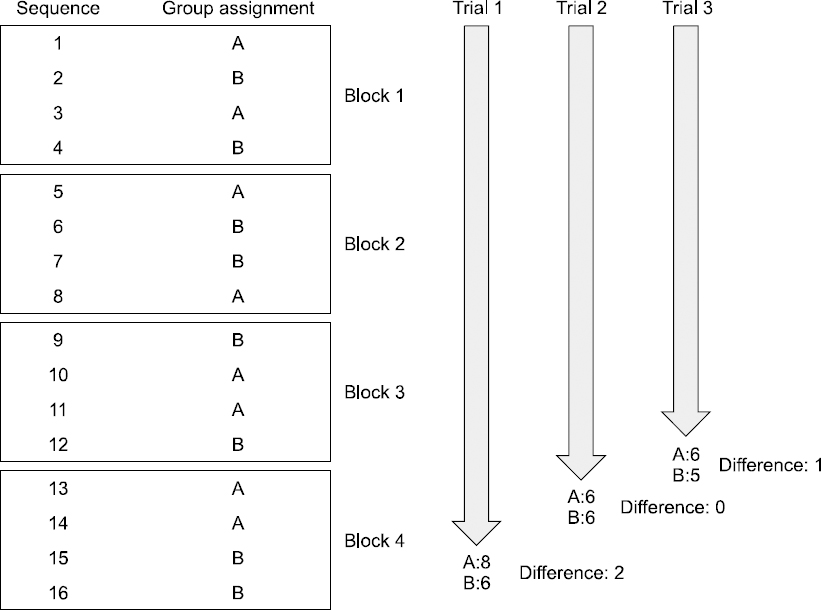
치료군 간 피험자 배정은 블록 단위로 배정비에 따라 균형을 맞추고 있으므로, 하나의 블록에 대한 실험이 끝날 때마다 피험자 배정은 다시 균형을 잡는다. 즉, 불균형은 한 블록 내의 배정을 이용하여 연구가 진행되는 동안에만 나타난다. 이 불균형은 항상 일정 범위 이내이며, 최대 크기는 블록 크기의 절반이다[11].
블록의 크기가 4인 블록 무작위 배정의 예를 들면(Fig. 2), 블록이 끝날 때는 정확히 균형이 맞춰지며(Trial 2는 세 번째 블록까지 완료되었다), 연구의 진행 중 발생할 수 있는 불균형의 최대 크기는 2이다(Trial 1).
블록 무작위 배정을 시행하는 방법은 1) 군의 수와 블록 크기에 의하여 생길 수 있는 모든 순열을 생성한 후, 생성된 순열 자체를 대상으로 단순 무작위 배정을 하는 방법과 2) 먼저 블록을 생성하고, 블록 내에서 피험자의 군 배정 순서를 임의로 정한 후, 블록 내에서 무작위 배정을 하여 순서를 다시 배치하는 방법이 있다[10].
예를 들어 2개의 군(A, B)을 대상으로 배정비는 1：1, 블록 크기 4인 블록 무작위 배정을 시행한다고 가정하자. 1) 방법에서는 우선 블록 내 배정비가 1：1인 경우에 대한 순열(위 예에서는 AABB, ABAB, ABBA, BAAB, BABA, BBAA와 같이 6가지 경우를 생성할 수 있음)을 생성한 후, 생성된6가지 순열을 단순 무작위 배정한다. 2) 방법에서는 한 블록 내 두 개의 A, 두 개의 B를 먼저 임의의 순서로 배치하며, 이 순서는 난수를 이용하여 재배치한다[10]. 먼저 블록 내 임의의 순서로 배치하였더니 AABB가 되었다고 가정한다. 이를 재배치하기 위하여 4개의 난수가 필요한데 0.3011, 0.4792, 0.7312, 0.1324가 나왔다. 이 난수에 가장 작은 수부터 큰 수까지 1, 2, 3, 4의 번호를 부여한다. 이 예에서는 2, 3, 4, 1이다. 이것을 앞의 AABB와 짝지으면 A = 2, A = 3, B = 4, B = 1이 되며, 1, 2, 3, 4의 순으로 배열하면 B, A, A, B로 재배치된다.
블록 무작위 배정의 단점으로는 첫째, 만일 블록에 대하여 맹검(blinding)이 이루어지지 않는다면, 다음 순서의 피험자가 어느 치료군에 배정될 지 어느 정도 예측이 가능하다는 점이다. 만일 블록 크기가 4인 연구에서 앞의 두 피험자가 대조군으로 배정되었다면, 다음 두 피험자는 시험군으로 배정된다는 것이 예측 가능하다. 이는 선택편향(selection bias)를 일으킬 수 있다[12]. 치료 약의 효과가 크게 나오기를 원하는 연구자는 시험군에 배정될 피험자의 확률이 높은 상황이 예측될 때, 치료가 잘 될 것으로 예상하는 피험자를 모집할 수도 있다. 이러한 선택편향을 일으키지 않기 위해서 블록을 생성하는 메커니즘을 밝히지 않거나, 블록 크기도 무작위 배정하거나, 이중 맹검을 사용할 수 있다.
둘째, 분석이 복잡하다. 블록 무작위 배정을 시행하였다는 점을 고려해서 분석하여야 한다[9]. 많은 경우에서와같이 이를 무시하고 분석하면, 검정력이 실제보다 낮아져서 더 보수적인 결과를 산출하게 된다.
마지막으로 블록 무작위 배정을 시행하여 피험자 수의 균형을 달성할 수는 있지만, 다른 예후 요인에서는 불균형이 생길 수 있다. 특히 예후 요인의 불균형이 결과에 영향을 미치는 요인일 경우 혼란변수(confounding factor)로 작용하여 연구 결과가 편향될 수 있다.
본문의 첫 부분에서 단순 무작위 배정의 예로 든 진통제의 연구에서와같이 고령의 피험자가 특정 치료군에 더 많이 배정되는 것을 막을 수 없으며, 이는 연구에 혼란변수로 작용하여 결과의 해석에 심각한 영향을 끼칠 수 있다[13]. 게다가 이러한 특정 공변량(혼란변수)의 불균형은 검정력을 낮출 수 있다. 따라서 임상 연구에서 피험자 수의 균형을 이루는 것만큼 공변량의 균형을 이루는 것 또한 중요하게 된다.
3. 층화 무작위 배정(Stratified randomization)
층화 무작위 배정은 단순 무작위 배정과 블록 무작위 배정에서 생길 수 있는 결과에 영향을 미칠 수 있는 예후요인의 불균형을 예방하고 제어할 필요성에 따라 생겨났다.
층화 무작위 배정의 수행 과정을 보자. 먼저, 연구자는 결과에 큰 영향을 미칠 것으로 예상되는 예후요인(층)을 조합하여 별도의 하위 그룹을 생성한다. 그런 후 피험자의 특성에 따라 피험자를 적절한 하위 그룹에 배정한다. 마지막으로 하위 그룹 내에서 배정된 피험자를 대상으로 단순 무작위 배정을 실시한다.
기관내삽관 후 혈압의 변동에 특정한 감압제가 미치는 영향에 대한 연구를 시행한다고 생각해 보자. 기관내삽관 후 혈압의 변동에 큰 영향을 미치는 여러 가지 예후요인이 있을 수 있지만, 여기에서는 고혈압 병력, 기도의 해부학적 이상 구조의 유무, 피험자의 연령이라고 가정하겠다. 이 예후요인들은 연구의 결과에 혼란변수로 작용한다. 만일 한 치료군에 고혈압 병력을 가진 사람, 기도의 해부학적 구조에 이상이 있는 사람, 연령이 많은 사람이 더 많이 배정된다면 이 연구의 결과는 실제효과보다 과장되거나 과소평가된, 즉 편향된 결과를 가져올 수 있을 것이다.
본 예에서 결과변수에 영향을 미칠 것으로 예상된 공변량(층)들을 고혈압 병력의 유무(있음, 없음), 기도의 해부학적 이상 유무(있음, 없음), 연령(40세 미만, 40세 이상 60세 미만, 60세 이상)로 나누어 볼 수 있다고 하자. 이 경우 하위 그룹은 12개(= 2 × 2 × 3)가 생성된다. 다음으로 피험자를 피험자의 특성에 따라 하위 그룹에 배정한 후 각 하위 그룹내에서 단순 무작위 배정을 시행한다. 층화는 꼭 필요한 예후요인만을 대상으로 시행하여, 층의 개수를 최소화해야 한다. 층의 개수가 증가하면 하위 그룹의 개수가 증가할 것이고 각 층에 배정되는 피험자의 수는 줄어들 것이기 때문이다. 즉 100명을 대상으로 연구를 시행하게 된다면 산술적으로 8–9명이 각 하위 그룹에 배정되지만, 여기에 성별이라는 하나의 공변량을 추가하게 된다면, 하위 그룹은 24개 (= 2 × 2 × 3 × 2)가 되며, 배정되는 피험자 수는 4–5명이 된다. 여기에 2개의 치료군을 대상으로 하는 연구임을 감안하면, 하위 그룹(블록) 내에서 각 군에 배정되는 피험자의 수는 2–3명이 된다. 또한, 하위그룹의 수가 증가하면 군 간 피험자 수의 차이가 증가할 수 있으며, 이 예에서 하위 그룹 내에서 치료군간 피험자 수가 1명씩만 차이가 나더라도 전체적으로 치료군간 최대 24명의 차이가 생길 수 있다.
층화 무작위 배정은 주로 소규모 연구에서 사용된다. 피험자 수가 많은 대규모 연구에서는 층화 무작위 배정을 시행하지 않더라도 예후 요인에 대한 분포가 치료군 간에 비슷해지는 반면, 피험자 수가 적은 소규모 연구에서는 예후 요인에 대한 분포가 차이 날 가능성이 높기 때문이다. 또한, 소규모 연구에서는 단순하고 구현이 어렵지 않아 유용한 방법이 될 수 있지만 대규모 연구에서는 많은 예후 요인을 제어하여야 하므로 구현이 복잡하게 되어 수행이 어려울 수 있다[14].
또한 모든 피험자의 특성을 배정 전에 파악할 수 있는 경우에만 사용할 수 있다. 모든 피험자의 일반적 특성을 확인하고, 이 중 결과에 영향을 줄 수 있는 예후 요인에 대해 층화를 미리 실시해야 하기 때문이다. 하지만, 대부분의 임상연구에서 피험자를 연속적으로 한 명씩 모집하므로 피험자의 특성을 미리 파악하기 어려우므로 층화 무작위 배정을 시행하기 어려운 경우가 많다[9].
층화 무작위 배정은 블록 무작위 배정과 마찬가지로 분석이 복잡하다. 하지만 그런 이유로 층화 무작위 배정을 무시하고 분석한다면, 검정력이 낮아진다. 따라서, 분석이 복잡하더라도 층화 무작위 배정을 반영하여 더 높은 검정력을 가지도록 하는 것이 필요하다.
근래 많이 시행되고 있는 다기관 임상연구에서는 각 치료군 간 피험자의 특성간의 균형을 맞추기 위해 기관을 하나의 층으로 반드시 포함할 것을 추천하고 있다[15].
배정확률에 변화를 주는 무작위 배정(Dynamic allocation randomization, Adaptive randomization)
조정 설계 방법(adaptive design method)은 1970년대에 처음 소개된 이후[16], 이후 점차 발전하면서 복잡한 방법과 구조를 갖게 되었다. 여기에서 조정(adaptation)은 임상 연구 수행 중 연구의 방법 및 절차에 변화를 가져오는 것을 의미하며, 연구수행절차(연구 참여의 적격성에 대한 기준, 약의 연구 용량, 치료 기간, 연구의 목적점[endpoint], 진단, 치료, 검사의 절차, 평가 기준 등)나 통계 절차(무작위 배정, 연구 디자인, 연구의 목표/가설, 표본수, 데이터 모니터링, 중간 분석, 통계 분석 등) 모두에 적용될 수 있다.
피험자를 각 치료군에 무작위로 배정하는 배정확률을 임상연구 수행 중에 바꾸는 조정 무작위 배정(adaptive randomization) 역시 조정의 한 형태이다. 각 군에 배정될 확률이 일정한 단순, 블록, 층화 무작위 배정과 달리 피험자가 각 군에 배정될 확률이 연구 도중 피험자의 배정 내용 혹은 치료 결과에 근거하여 바뀌는 무작위 배정이다. 무작위 배정은 처치(군 배정), 공변량(예후 요인), 치료 결과 등에 대해 진행된다.
조정 무작위 배정은 무작위 배정확률에 변화가 생기는 원인에 따라 일반적으로 치료 조정 무작위 배정(treatment adaptive randomization) [12,16-19], 공변량 조정 무작위 배정(covariate adaptive randomization) [9,18,20,21], 반응 조정 무작위 배정(response adaptive randomization) [20-24]으로 나뉜다.
1. 치료 조정 무작위 배정(Treatment adaptive randomization)
피험자의 배정 시점까지 각 치료군에 무작위 배정된 피험자 수에 따라 현재 피험자의 배정확률을 조정하는 방법이다.
편향된 동전 무작위 배정(Biased coin randomization): 피험자는 차례대로 연구에 참여하고, 연구 전체 피험자 수가 지정되지 않았을 때, 치료군 간의 배정 비율의 균형을 맞추기 위해 사용되는 방법이다. 이 방법은 동일한 목적(치료군 간의 피험자 수의 균형을 맞추려는)을 가지는 블록 무작위 배정보다 선택 편향(selection bias)에 영향을 덜 받는 것으로 알려져 있다[9].
이 방법은 Efron [17]이 처음 소개하였다. 이 방법에서 새로 모집된 피험자가 어떤 치료군에 배정될 확률은 현재 치료군 간 피험자 수의 균형에 의해 결정된다[10]. 피험자가 연구에 참여할 때마다, 그 시점까지 치료군 간에 피험자 수의 차이를 계산한다. 예를 들어, 두 치료군을 가진 연구에서, 치료군 간에 표본수가 균형이 맞을 경우 두 군에 피험자가 배정될 확률은 각각 0.5로 같게 되지만, 두 군 간 대상 수의 차이가 역치(d) 이상이면, 피험자가 적게 배정된 군에 배정될 배정확률(p)을 높여 치료군 간의 균형이 맞도록 한다(Table 2).
Table 2
Biased Coin Randomization
| Difference in Current Cumber of Subjects between Groups | Probability of Assignment to group A | Probability of Assignment to group B |
|---|---|---|
| NA − NB > d | 1 − p | p |
| NB − NA > d | p | 1 − p |
| −d < NA − NB < d | 1/2 | 1/2 |
여기에서 역치(d)와 배정확률(p)는 연구자에 의해 사전 결정되며, 배정확률(p)은 1/2보다 큰 값으로 일반적으로 Efron 이 제안한 2/3가 대체로 사용된다[17].
이 방법은 구현이 쉽고 각 피험자가 연구에 참여하자마자 무작위 배정을 시행하고 각 치료군 간 표본 수의 균형을 달성할 수 있도록 고안되었지만, 치료군 간에 피험자 수의 불균형이 큰 경우와 작은 경우를 구별하여 불균형에 대처하지 못한다는 단점이 있다.
예를 들어 1) A군에는 1명, B군에는 4명이 배정된 경우와 2) A군에는 13명, B군에는 16명이 배정된 경우를 가정해 보자. 군 간 표본 수의 차이는 1)의 경우와 2)의 경우 모두 3으로 같다. 하지만 1)의 경우 피험자 수의 불균형이 상대적으로 더 크다는 것을 알 수 있으며, 이 경우 A군에 더 많은 피험자를 배정하여 불균형을 줄이는 것이 중요한 반면, 2)의 경우 군 간에 피험자 수가 전반적으로 균형을 이루는 것으로 보이며, 다음 피험자가 A군에 배정될 필요가 1)의 경우보다는 적을 것이다. 하지만 편향된 동전 무작위 배정에서는 피험자가 각 군에 배정될 확률에 미치는 요인은 두 군 간의 표본 수의 차이의 크기뿐으로, 불균형의 상대적 크기가 배정될 확률에 영향을 주지 않는다.
조정 편향된 동전 무작위 배정(Adaptive biased coin randomization): 편향된 동전 무작위 배정이 배정확률에 불균형의 상대적 크기를 반영하지 못한다는 점 때문에 조정 편향된 동전 무작위 배정이 Wei [16,19]에 의해 고안되었다.
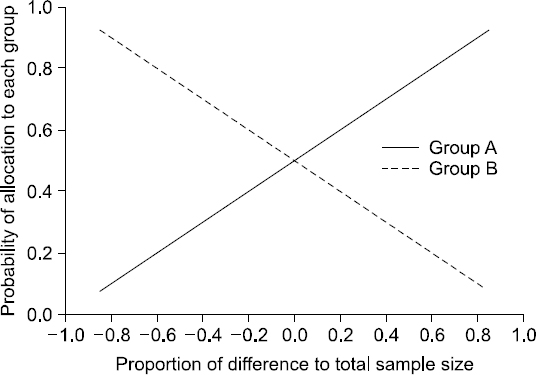
이 방법에서는 편향된 동전 무작위 배정과 유사하게 피험자 수 차이에 대한 역치(d)를 연구 시작 전에 결정한다. 하지만 편향된 동전 무작위 배정의 경우 배정확률(p)이 사전에 지정되어 있으며 변하지 않는 반면, 조정 편향된 동전 무작위 배정의 경우 피험자수의 차이(NA − NB)를 전체 피험자 수(NA + NB)로 나눈 값이 새로 참여하는 피험자의 배정확률에 반영된다(NA: A군에 배정된 피험자 수, NB: B군에 배정된 피험자 수). A군의 피험자 수가 많다고 할 때, 피험자 수의 차이가 커짐에 따라 새로 참여한 피험자가 B군에 배정될 확률은 증가하고, A군에 배정될 확률은 감소한다. 피험자가 A군에 배정될 확률과 B군에 배정될 확률의 합은 1이 된다(Fig. 3).
조정 편향된 동전 무작위 배정 방식은 Friedman이 제시한 항아리 모델(Urn model)을 이용하면 용이하게 구현할 수 있는데 그 방법은 다음과 같다. 먼저 항아리에 동일한 수의 하얀 공(A군에 배정)과 까만 공(B군에 배정)을 넣는다. 공을 하나 꺼내서 하얀 공이면, 피험자를 A군에 배정하고 꺼낸 하얀 공과 새로운 까만 공을 항아리에 넣는다. 꺼낸 공이 까만 공이면 B군에 배정하고, 꺼낸 까만 공과 새로운 하얀 공을 항아리에 넣는다. 이렇게 되면 추출된 공의 수만큼 전체 공의 수는 증가하게 되며, 현재 배정된 반대편 공의 수가 증가하게 된다.
이럴 경우 각 군에 배정된 표본 수의 차이를 전체 공의 수로 나눈 값 (NA: 전체 하얀 공의 수, NB: 전체 검은 공의 수, nA: 최초 하얀 공의 수, nB: 최초 검의 공의 수, nA = nB, mA: 새로 넣은 하얀 공의 수, mB: 새로 넣은 검은 공의 수)의 절반을 0.5에 더하거나 뺀 값만큼 각 치료군에 배정될 확률을 가지게 된다.
이 방법을 이용하면 표본 크기 불균형의 상대적 크기를 피험자가 치료군에 배정될 확률에 반영할 수 있게 된다. 앞서 편향된 동전 무작위 배정 예제에서는 피험자 수의 차이가 역치를 넘을 경우 배정확률이 1) A군에는 1명, B군에는 4명이 배정된 경우와 2) A군에는 13명, B군에는 16명이 배정된 경우 모두 동일하게 되나, 조정 편향된 무작위 배정을 이용하면 달라진다. 최초 항아리에서 A군과 B군에 각각 2개씩으로 시작한다고 했을 때, A군에 배정될 확률이 1)의 경우에서는 0.625, 2)의 경우에서는 0.545가 된다. 따라서 군간 표본 수의 불균형이 심각할수록 피험자가 적은 군에 배정될 확률이 높아지게 되므로 표본크기의 균형을 맞추는 데 더 효율적인 방법이 된다.
2. 공변량 조정 무작위 배정(Covariate adaptive randomization)
치료 조정 무작위 배정은 치료군 간 피험자 수의 균형을 맞추는 것이 주요 목적이다. 하지만 배정확률이 일정한 무작위 배정인 단순 무작위 배정과 블록 무작위 배정에서와 같이 중요한 공변량에서 치료군 간의 불균형을 야기할 수 있으며, 이는 연구결과의 해석에 영향을 줄 수 있다.
공변량 조정 무작위 배정은 이전에 배정된 피험자의 공변량을 고려하여 새로운 피험자를 특정한 치료군에 순차적으로 배정한다. 여러 방법이 소개되었으나, 대표적인 방법은 최소화법(minimization)인데, 몇 가지 공변량에 대한 피험자 수의 불균형을 평가하여 최소화시키는 방법이다[9].
본 논문에서는 Frane [18]에 의해 제시된 방법을 이용하여 예를 들어보도록 하겠다. 순서는 다음과 같다.
1) 먼저 새로 모집되는 피험자를 임의로 한 치료군에 배정해 본다. 2) 배정 후 각각의 공변량에 대한 Pearson χ2 적합도 검정 통계량을 계산한다. 3) 모든 공변량 중에서 Pearson χ2 적합도 검정 통계량이 최대인 공변량을 확인한다. 4) 처음 배정된 치료군에서 피험자를 뺀 후 다른 치료군에 배정하고 1–3단계를 반복한다. 5) 피험자를 각 치료군에 배정 후 1–3단계를 반복할 때마다 확인된 최대 Pearson χ2 적합도검정 통계량 중에서 어느 치료군에 배정하였을 때 최솟값을 가지는지 확인한다. 6) 최소 Pearson χ2 적합도검정 통계량을 가지는 치료 군에 피험자를 배정한다.
앞서 예를 들었던 특정 감압제가 기관내삽관 후 혈압의 변동에 미치는 영향에 대한 연구를 시행한다고 하자. 결과에 영향을 미치는 공변량은 고혈압 병력의 유무(있음, 없음), 기도의 해부학적 이상 유무(있음, 없음), 연령(40세 미만, 40세 이상 60세 미만, 60세 이상)이다. 현재까지 총 20명의 피험자가 모집되었으며, 공변량의 특성은 다음과 같다(Table 3).
Table 3
Example of Covariate Adaptive Randomization
| Group A | Group B | ||
|---|---|---|---|
| Hypertension | Yes (n) | 3 | 4 |
| No (n) | 9 | 4 | |
| Airway Anomaly | Yes (n) | 2 | 3 |
| No (n) | 10 | 5 | |
| Age (yr) | < 40 (n) | 4 | 2 |
| 40 ≤ < 60 (n) | 5 | 2 | |
| 60 ≤ (n) | 3 | 3 | |
고혈압의 병력을 가지고, 기도의 해부학적 이상이 없으며, 연령이 60세 이상인 피험자가 새로이 모집되었다고 하자. 먼저 A군에 피험자를 배정해 보고, 각각의 Pearson χ2 적합도 검정 통계량을 계산한다. 이 경우 Pearson χ2 적합도 검정 통계량은 고혈압의 병력에서는 1.615, 기도의 해부학적 이상 유무에서는 1.335, 연령에서는 0.324이 되게 된다. 여기에서 가장 큰 Pearson χ2 적합도 검정 통계량은 고혈압 병력에서의 1.615가 된다.
다음으로 B군에 피험자를 배정해 보고, 각각의 Pearson χ2 적합도 검정 통계량을 계산한다. 이 경우 Pearson χ2 적합도 검정 통계량은 고혈압의 병력에서는 0.875, 기도의 해부학적 이상 유무 0.787, 연령에서는 1.349가 되게 된다. 여기에서 가장 큰 Pearson χ2 적합도 검정 통계량은 연령에서의 1.349가 된다.
A군에 배정하였을 때 고혈압 병력에서의 Pearson χ2 적합도 검정 통계량 1.615와 B군에서 배정하였을 때, 연령에서의 Pearson χ2 적합도 검정 통계량 1.349 중 작은 값을 가지는 B군에 피험자를 배정한다. 이런 방식을 적용하는 이유는 B군에 배정했을 때 공변량의 불균형에 대한 최댓값이 가장 적어지게 되어 불균형이 최대로 발생하는 것을 막을 수 있기 때문이다.
본 논문에서는 편의상 2개의 치료군과 3개의 공변량을 가지는 경우로 예를 들었지만, 더 많은 치료군과 공변량을 가지는 경우에도 확장하여 사용할 수 있다.
이 방법을 적용하게 되면, 무작위 배정 중에 치료군 간의 공변량 전반에 대한 균형을 유지할 수 있다. 따라서 임상연구에서 공변량 조정 무작위 배정이 권장되기도 한다[25].
하지만 이 방법 역시 단점들이 존재한다. 첫째, 공변량이 많을 경우 수행이 복잡하고, 분석을 제대로 하기 위해서는 시뮬레이션 등을 통하여 유의수준을 파악해야 한다. 둘째, 첫 번째 피험자만 무작위 배정이 될 뿐 다음 피험자부터는 이전 피험자의 특성에 의거하여 군이 결정되므로 선택편향의 가능성이 여전히 있다[15].
3. 치료 효과 조정 무작위 배정(Response adaptive randomization)
치료 효과 조정 무작위 배정은 결과 조정 무작위 배정(outcome adaptive randomization)이라고도 하며, 연구에서 얻어진 치료 효과나 결과에 대한 자료를 이용하여 피험자의 배정을 시행하게 된다. 이 방법은 피험자에게 이득이 되는 치료 방법에 더 많은 피험자가 배정될 수 있게 하려는 윤리적 이유에서 개발되었다[26].
승자 우선 배정법(Play-the-winner allocation rule): 승자 우선 배정법은 Zelen [23]에 의해 두가지 치료군과 이분형 변수(성공/실패)의 결과를 갖는 연구를 위해 설계되었다. 이 방법에서 새로 모집된 피험자의 각 치료군에 대한 배정은 모집 직전 피험자의 결과에 따라 달라진다. 따라서 이 방법은 치료에 대한 반응이 빨라 치료 효과나 결과를 빠르게 확인할 수 있는 경우에 적용할 수 있다.
먼저 단순 무작위 배정을 실시하여 첫 피험자를 배정한다. 만일 이 피험자에 대한 치료효과나 결과가 성공적이면 다음 피험자를 같은 군에 배정하고, 성공적이지 못하면 다른 군에 배정한다(Table 4).
Table 4
Example of Play the Winner Rule
| Subject sequence | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Group A | S | S | F | S | F | S | S | |||
| Group B | F | S | F |
이 방법은 치료 효과나 결과가 좋은 치료군에 더 많은 피험자를 배정할 수 있다는 장점이 있다. Table 4에서 만일 A군에 적용된 치료가 더 효과적이라고 하더라도, 단순 무작위 배정을 하였다면 10명의 피험자 중 대략 5명이 배정되었겠지만, 승자 우선 배정법을 사용하면 A군에 7명이 배정된다.
Table 4의 예에서 A군이 더 좋은 치료 효과나 결과를 가져오는 치료라고 하였을 경우, 단순 무작위 배정을 하였다면 총10명의 피험자를 대상으로 하였으므로 A군에 5명의 피험자가 배정되었겠지만, 이 방법을 사용하면 7명의 피험자가 배정되어 배정된 피험자 수가 증가한다. 하지만 이 방법 또한 연구자가 다음 피험자가 어느 군으로 배정될지 알 수 있으므로, 선택편향을 일으킬 수 있다.
무작위화를 동반한 승자 우선 배정(Randomized play the winner rule): 무작위화를 동반한 승자 우선 배정(randomized play the winner rule)은 항아리 모델(Urn model)을 기반으로 한 간단한 확률 모델을 적용하여, 임상 시험에서 피험자를 순차적으로 무작위 배정하게 된다[24]. 각 시점에서 각 군에 배정될 확률은 그 시점까지 관측된 성공 확률에 의해 결정되며, 각 피험자의 결과가 알려질 때마다 배정될 확률은 지속적으로 변경된다.
이 방법은 조정 편향된 동전무작위 배정에서와같이 먼저 항아리에 동일한 수의 하얀 공(A군에 배정)과 까만 공(B군에 배정)을 넣는다. 피험자가 모집되면 공을 꺼내 각 군에 배정하고 그 공은 다시 항아리에 넣는다. 피험자의 치료 결과를 알 수 있으면 결과에 따라 항아리 안의 공의 수는 매번 바뀌게 된다. A 치료가 성공하거나, B 치료가 실패하면 지정된 수 만큼 A군에 배정하는 하얀 공을 항아리에 추가한다. 반대로 B 치료가 성공하거나, A 치료가 실패하면 지정된 수 만큼 B군에 배정하는 까만 공을 항아리에 추가한다. 이러한 방식으로 항아리에는 치료 효과가 우수한 치료에 해당하는 공의 수가 점차 많아지게 되며, 이에 따라 피험자가 성공적인 치료를 받게 될 확률이 증가한다.
이 방법을 이용하게 되면, 현재 수행 중인 임상시험에서 새롭게 얻어진 치료 효과나 결과에 대한 정보를 적용함으로써, 효과나 안전성에서의 차이를 더 빨리 발견하고 연구에 변화를 줄 수 있게 된다. 따라서 연구의 윤리성(ethicality) 및 유연성(flexibility) 측면에서 장점을 가진다.
하지만 몇 가지의 설계, 논리, 통계학적, 실제 적용에서의 문제로 그 사용이 제한된다[22].
첫째, 신생아에게 extracorporeal membrane oxygenation 적용했던 연구처럼[27] 피험자를 충분히 모집하지 못하거나, 치료효과가 매우 명확한 경우, 치료군 간 피험자 수에 불균형을 가져올 수 있다.
이 연구에서는 오직 12명의 피험자만 모집되었으며, 피험자 중 1명만 대조군으로 배정되었다. 이런 피험자 수의 불균형과 부족은 검정력을 크게 감소시킨다.
둘째, 진행 중인 연구에 변화된 방식을 적용하게 되면 완전히 다른 연구로 변경될 수 있어, 연구자들이 원래 연구에서 알고자 했던 진정한 치료 효과에 대한 추정을 하기가 어려워지게 된다. 이는 연구 종료 후 분석을 어렵게 하는 요인이 된다.
셋째, 연구 도중 결과를 알게 되므로 맹검이 이루어지기 어려워 선택 편향을 일으킬 수 있다.
넷째, 대규모 연구나 치료 혹은 시험 기간이 긴 연구에서는 적용이 어렵다.
위에 언급한 여러 이유 때문에 배정확률에 변화를 주는 무작위 배정(특히 치료 효과 무작위 배정)은 배정확률이 일정한 무작위 배정보다 장점이 없거나, 새로운 윤리적 문제를 일으킬 수 있다는 주장도 있다[28,29]. 따라서 아직은 임상연구 방법의 주류는 아니며[26,30], 배정확률이 일정한 무작위 배정을 이용한 연구가 임상연구의 표준이 되고 있다[31]. 하지만 배정확률에 변화를 주는 무작위 배정에서 생길 수 있는 여러 가지 문제점을 극복하기 위한 다양한 방법들이 개발되면서[32-34], 근래에는 많은 임상연구들이 성공적으로 수행되고 있다.
EXCEL을 이용한 무작위 배정
Microsoft Excel은 상용 프로그램이긴 하나 널리 보급되어 있기 때문에 무작위 배정 순서를 생성하는 데 가장 많이 사용되는 소프트웨어 중 하나이다. 여기에서는 Microsoft Excel 2010을 이용하여 단순 및 블록 무작위 배정을 시행하는 간단한 예를 들어 보이도록 하겠다.
단순 무작위 배정(Fig. 4)
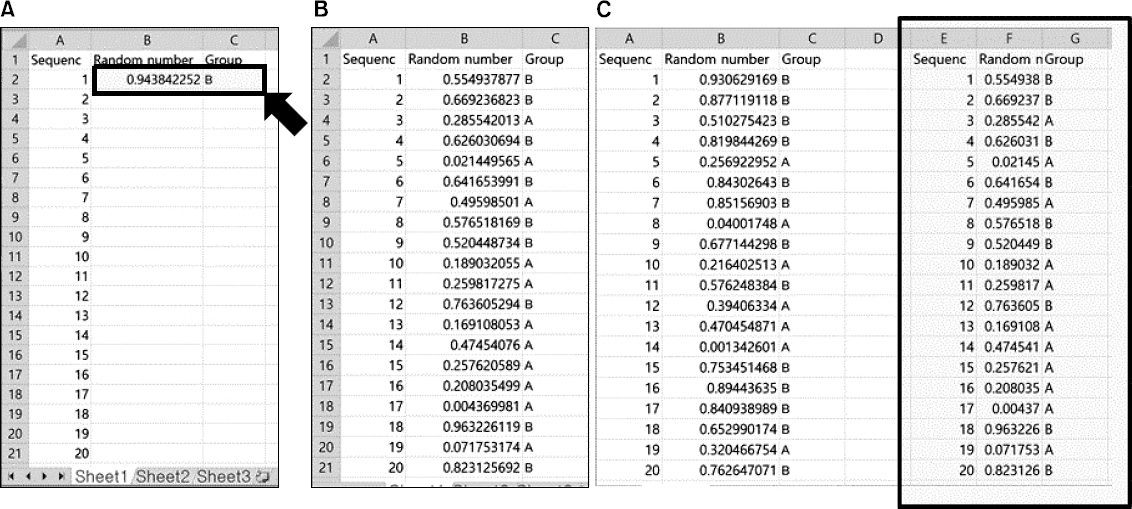
20명의 피험자를 A, B 두 개의 군에 단순 무작위 배정을 한다고 가정하자. 먼저 빈 Excel 스프레드시트를 열고, 셀 A1, B1, C1에 머리글로 Sequence, Random number와 Group을 각각 입력한다. 다음으로 셀 A2부터 A21까지 1에서 20까지의 수를 순서대로 입력한다. 번호를 순서대로 입력하기 위해서는, 셀 A2에 1을 입력하고 셀의 오른쪽 하단 모서리를 클릭한 다음 Ctrl 키를 누른 상태로 아래쪽으로 20개의 행을 드래그하면 된다. 다음으로 B2에 함수 = rand()을 입력한다. 이 함수는 0에서 1 사이의 범위에서 균등분포(uniform distribution)되는 난수를 생성한다. 다음으로 C2에 함수 =IF(B2>0.5,”B”,”A”)를 입력한다. IF 함수는 조건에 따라 2가지 이상의 다른 결과를 도출할 수 있도록 해주는 함수로, 여기에서는 생성된 난수가 0.5 초과이면 B군으로 그렇지 않은 경우 A군으로 배정한다. 셀 B2에서 마우스 왼쪽 단추를 클릭한 후 클릭한 상태로 셀 C2까지 드래그하여 두 셀을 지정한 후 Fig. 4A에서 화살표로 표시된 위치에서 마우스 왼쪽 단추를 클릭한 상태로 아래로 드래그하여 나머지 19개의 행에 함수를 복사한다. 그러면 Fig. 4B와 같은 형태로 셀들이 채워지게 된다. 여기에서 생기는 문제는 스프레드시트가 업데이트될 때마다 난수가 자동으로 변경된다는 점이다. 숫자를 변경되지 않도록 하려면 셀 A1부터 C21까지 드래그하여 전체를 선택한 후, 마우스 오른쪽 단추를 클릭하여 복사를 선택한 다음, 다시 복사하고자 하는 위치를 선택한 후 마우스 오른쪽 버튼을 선택하여 붙여넣기-값을 설정하면 된다. Fig. 4C에서 새로 생긴 오른쪽 사각형 내의 값은 Fig. 4B와 동일한 반면 왼쪽의 원래 자료는 업데이트됨과 동시에 난수와 군 배정이 바뀌었음을 확인할 수 있다. 또한 A군에 7명, B군에 13명이 배정됨으로써, 단순 무작위 배정에서 발생할 수 있는 문제점 중의 하나인 군 간의 피험자 수 불균형이 발생하였음을 확인할 수 있다.
블록 크기가 일정한 블록 무작위 배정(Fig. 5)
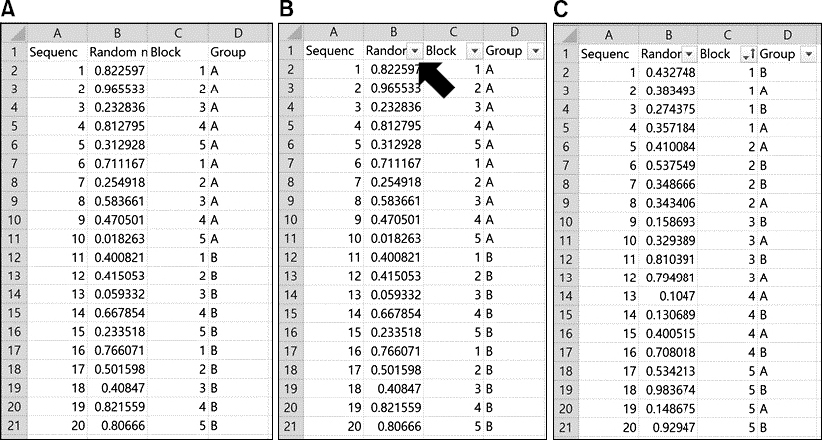
20명의 피험자를 A, B 두 개의 군에 블록 크기 4, 배정비 1：1인 블록 무작위 배정을 한다고 가정하자. 먼저 빈 Excel 스프레드시트를 열고, 셀 A1, B1, C1, D1에 머리글로 Sequence, Random number, Block과 Group을 각각 입력한다. Sequence 열인 셀 A2에서 A21까지는 1부터 20까지의 수를 순서대로 입력하고, Block 열인 셀 C2에서 C21까지는 1에서 5까지의 수를 4번 반복하여 입력한다. 전체 20명의 피험자를 대상으로 블록 크기가 4인 배정을 시행하므로 1에서 5까지의 수는 해당 블록의 순서를 의미한다. 마지막으로 Group 열인 셀 D2에서 D21까지에 A 10개, B 10개를 이어서 입력한다. 다음으로 셀 B2에서 B21까지에는 함수 = rand()을 입력한다. 그러면 Fig. 5A와 같은 스프레드시트를 만들 수 있다. 다음으로 머리글 B1에서 D1까지 드래그하여 선택하고, 홈-정렬 및 필터-필터를 선택한다. 그러면 Fig. 5B와 같이 머리열의 오른쪽에 스크롤 바가 생기는 것을 알 수 있다. 여기에서 B2의 스크롤 바를 클릭한 후 오름차순 정렬을 선택한다. 다음으로 C2의 스크롤 바를 클릭한 후 오름차순 정렬을 선택한다. 그러면 Fig. 5C와 같은 화면을 생성할 수 있다. 여기에서 피험자가 모집되는 순서(sequence)에 따라 군 배정(group)을 실시하며, 블록은 1에서 5까지의 블록이 블록 크기가 4이라는 것을 알 수 있다. 단순 무작위 배정에서와 같이 함수 = rand()는 스프레드시트가 업데이트될 때마다 난수가 바뀔 수 있으므로, 선택하여 붙여넣기-값을 이용하여 복사한다.
블록크기의 무작위 배정을 동반한 블록 무작위 배정(Fig. 6)
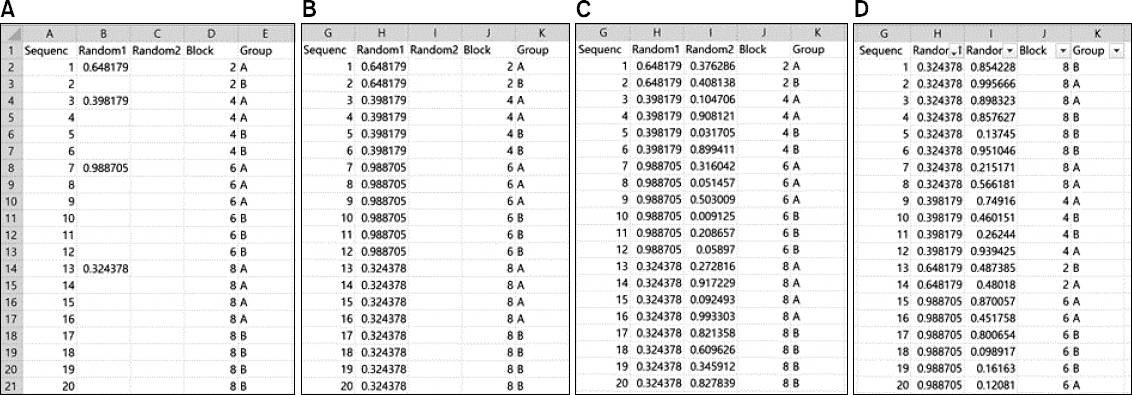
선택편향을 일으키지 않기 위해서 블록의 크기에 무작위 배정을 사용할 수 있다. 20명의 피험자를 A, B 두 개의 군에 배정비 1：1인 블록 무작위 배정을 한다고 가정하자. 본 예에서 블록 크기는 2, 4, 6, 8을 사용할 것이다.
먼저 빈 Excel 스프레드시트를 열고, 셀 A1, B1, C1, D1, E1에 머리글로 Sequence, Random1, Random 2, Block, Group을 각각 입력한다. Fig. 5A와 같이 Sequence 열인 셀 A2에서 A21까지에는 1부터 20까지의 수를 순서대로 입력하고, Block 열인 셀 C2에서 C21까지에는 2를 2개, 4를 4개, 6을 6개, 8을 8개 순서대로 입력한다. 여기에서 각 숫자는 블록의 크기를 의미한다. 다음으로 Group 열인 셀 D2에서 D21에는 블록 크기의 절반에 해당하는 수의 A와 B를 순서대로 입력한다. 다음으로 각 블록의 시작인 셀 B2, B4, B8, B14에 함수 = rand()을 입력한다. 그러면 Fig. 6A와 같은 스프레드시트를 만들 수 있다. 함수 = rand()로 인해 스프레드시트가 업데이트될 때마다 난수가 바뀔 수 있으므로, 선택하여 붙여넣기-값을 이용하여 복사한다. 그렇게 되면 B 열에 있는 함수는 숫자로 변환되어 업데이트될 때마다 바뀌지 않는다. 셀 B2, B4, B8, B14의 오른쪽 하단의 모서리를 클릭하여 각 셀 아래셀에 복사하여 넣으면 Fig. 6B와 같이 된다. 다음으로 머리글 Random2 아래 20개의 셀에 = rand()을 입력한다. 그러면 Fig. 6C와 같이 된다. 다음으로 머리글 Random1부터 Group까지 드래그하여 선택하고, 홈-정렬 및 필터-필터를 선택한다. 다음으로 Random2 오름차순 정렬, Random1 오름차순 정렬을 시행하면 Fig. 6D와 같은 화면이 생성된다. 여기에서 블록 크기의 무작위 배정을 동반한 블록 무작위 배정이 시행되었음을 확인할 수 있다.
결론
무작위 배정은 배정 과정에 연구자의 주관을 배제하고 각 치료군에 배정될 확률을 같아지도록 한다. 이에 따라 중요한 공변량들을 유사하게 만들어 치료군 간의 비교가능성을 보장하며 통계적 검정에 타당성을 부여한다. 따라서 임상시험을 실시하는 데 필수적인 요소가 되고 있다.
무작위 배정을 위한 방법은 다양하며, 다양한 만큼 나름의 특성과 장점이 있으나 단점 또한 지니고 있다. 무작위 배정의 방법에 따라서는 실제 무작위 배정을 시행하는 이유로 알려진 것들도 위배하는 경우 역시 있다. 예를 들어 치료군, 공변량, 치료효과, 결과에 대한 정보를 무작위 배정 과정에서 이용하여 연구자의 주관을 배제하기 어렵게 할 수도 있으며, 각 군에 배정될 확률이 완전히 같도록 보장하지 못할 수도 있으며, 중요한 공변량에 차이가 생겨 비교가 어려워지기도 한다. 이를 극복하기 위하여 다양한 연구, 시행, 분석방법들이 새로 소개되어 시행되기도 하지만, 이러한 단점들을 모두 극복할 수는 없으며 실제 임상에서 연구를 진행하고 있는 연구자들이 이해하거나 적용하는 데 어려움이 있다.
저자는 지금까지 많이 사용되면서도 기초적인 몇 가지 무작위 배정을 간략히 소개하였다 각 무작위 배정은 어떤 시험에서는 적절하고 장점을 가질 수 있지만, 다른 시험에서는 적절하지 못하거나 시행할 수 없기도 하다. 우리 연구자는 다양한 무작위 배정의 특성과 장단점을 이해하여 실제 연구에 적용하고 활용할 수 있어야 하며, 종료 후 해석을 통해 타당한 결과를 도출할 방법을 상황에 맞게 선택할 수 있어야 한다.
XML Download