This article has been
cited by other articles in ScienceCentral.
Abstract
Missing values and outliers are frequently encountered while collecting data. The presence of missing values reduces the data available to be analyzed, compromising the statistical power of the study, and eventually the reliability of its results. In addition, it causes a significant bias in the results and degrades the efficiency of the data. Outliers significantly affect the process of estimating statistics (e.g., the average and standard deviation of a sample), resulting in overestimated or underestimated values. Therefore, the results of data analysis are considerably dependent on the ways in which the missing values and outliers are processed. In this regard, this review discusses the types of missing values, ways of identifying outliers, and dealing with the two.
Go to :

Keywords: Bias, Data collection, Data interpretation, Statistics
Introduction
Missing values and outliers are frequently encountered during the data collection phase of observational or experimental studies conducted in all fields of natural and social sciences.
Missing values can arise from information loss as well as dropouts and nonresponses of the study participants. The presence of missing values leads to a smaller sample size than intended and eventually compromises the reliability of the study results. It can also produce biased results when inferences about a population are drawn based on such a sample, undermining the reliability of the data. As a part of the pretreatment process, missing data are either ignored in favor of simplicity or replaced with substituted values estimated with a statistical method. In general, the analysis of missing values involves the consideration of efficiency, handling of missing data and the resulting complexity in analysis, and the bias between missing and observed values.
The other problem is that of outliers, which refers to extreme values that abnormally lie outside the overall pattern of a distribution of variables. When weight data are collected, a value of 250 kg cannot fit into the normal distribution for weights; it thus represents an outlier. Outliers result from various factors including participant response errors and data entry errors. In a distribution of variables, outliers lie far from the majority of the other data points as the corresponding values are extreme or abnormal. The outliers contained in sample data introduce bias into statistical estimates such as mean values, leading to under- or over-estimated resulting values. Dealing with outliers is essential prior to the analysis of the data set containing outlier. This involves modifying outliers after identifying their sources or replacing them with substituted values.
The different approaches for handling missing values and outliers can drastically change the results of data analysis. Therefore, adequate treatment of missing data and outliers is crucial for analysis. In this review paper, we discuss the types of missing values and different methods used to identify outliers and to handle missing values and outliers efficiently.
Go to :

Types of Missing Values
According to previous studies, missing values are divided into two categories: missing completely at random (MCAR) and no missing at random (NMAR), depending on the types of missingness that occurred (
Table 1) [
1].
Table 1
Types of Missing Values
|
Types of missing values |
Description |
Possible causes |
|
Missing completely at random |
Missing data occur completely at random without being influenced by other data. |
Consent withdrawal, omission of major exams, death, discontinued follow-up and serious adverse reactions. |
|
Missing at random |
Missing data occur at a specific time point in conjunction with participant dissatisfaction with study outcomes and ongoing participation |
Refusal to continue measurements. |
|
Not missing at random |
Missing data occur when a patient who is not satisfied with study outcomes performs the required measurements on his own, before the scheduled measurement. |
If a patient finds the results of self-measurement dissatisfactory in addition to dissatisfaction related to the study, the patient may refuse further measurements. |

To explain the types of missing values, the following elements are defined under the assumption that the total number of study participants is ‘i’ and the total number of measurements is ‘j’.
Yij: The ‘j’th measurement value for the ‘i’th patient, i = i, … , I, j = 1, … , J
Yi(observation): A vector created based on measurement values of the ‘i’ th patient
Yi(missing): A vector created based on missing values of the ‘i’th patient.
Ri = (Ri1, Ri2, … Rij … RiJ): A vector function indicating whether the ‘i’th patient's ‘j’th measurement value is a missing value.
Rij = 1 if Yij is a missing value
Rij = 0 if Yij is a measurement value
Missing completely at random (MCAR)
If Yi(observation), Yi(missing), and Ri are independent, Yi(missing) indicates a value MCAR. That is, any particular data are missing independently of other data in a data set. The missingness occurs completely at random during the course of study, if a study participant is suddenly absent from measurements or drops out any time before the study ends.
For instance, a patient may not show up for his or her appointment at a specific time point (‘j’) or may drop out of studies due to a specific reason such as withdrawal of consent, omission of major examinations, death, discontinued follow-up, and development of serious adverse reactions. In each case, the corresponding data becomes missing completely at random.
Missing at random (MAR)
While Ri and Yi(observation) are dependent and Ri and Yi(missing) are independent, Yi(missing) is the value missing at random. Thus, the occurrence of MAR is associated more with Yi(observation) and has no relation with Yi(missing). Data missing at random can occur at a specific time in conjunction with participant dissatisfaction with study outcomes.
For instance, a patient may find the measurement results unsatisfactory when the patient is about to take the ‘j’th measurement and intentionally omits the ‘j’th measurement. As a result, the corresponding data becomes missing at random. Missing data at random occur more frequently than missing data completely at random in clinical studies.
Not missing at random (NMAR)
If Ri and Yi(observation) are dependent and Ri and Yi(missing) are overly dependent, Yi(missing) represents the value not missing at random; that is, the occurrence of NMAR is associated with both Yi(observation) and Yi(missing). The data not missing at random can also occur in conjunction with participant dissatisfaction with study outcomes. The difference from MAR is that the participants perform the required measurements on their own.
For instance, a patient who is not satisfied with measurement results performs the required measurements on his own rather than undergoing the ‘j’th measure. If the results of self-measurement are consistent with those of the previous measures, the patient may intentionally omit the ‘j’th measurement. The corresponding data becomes not missing at random.
Go to :

Methods for Handling Missing Values
Many studies have discussed the analysis of a data set containing missing values [
23]. In this paper, we address the different methods available for treating and analyzing missing values.
Complete case analysis
This method uses only the data of variables observed at each time point for analysis after removing all missing values. While the simplicity of analysis is an advantage, reduced sample size and lower statistical power are disadvantages because drawing statistical inferences becomes difficult during analysis. It is the most commonly used method in statistical analysis programs such as SPSS and SAS to handle missing values.
Available case analysis
This technique deals with only the data available for each analysis. It allows a larger sample size than that used for complete case analysis. However, this approach causes sample sizes to vary between the variables used in analysis.
Imputation analysis
Imputation involves replacing missing values with substituted values obtained from a statistical analysis to produce a complete data set without missing values for analysis. Imputations can be created by using either an explicit or an implicit modeling approach. The explicit modeling approach assumes that variables have a certain predictive distribution and estimates the parameters of each distribution, which is used for imputations. It includes different methods of imputation by mean, median, probability, ratio, regression, predictive-regression, and assumption of distribution. The implicit modeling approach focusses on computing an algorithm required to generate accurate imputation values, if possible. Common implicit modeling methods include hot-deck imputation, cold-deck imputation, and substitution. A combination of explicit and implicit modeling methods is also used. In this review paper, we have not described each imputation method in detail.
Go to :

Methods for Identifying Outliers
Given that the outliers are data points lying far away from the majority of other data points, outliers in the data that is not normally distributed do not require identification. As most statistical tests assume that data are normally distributed, outlier identification should precede data analysis. Different methods are used to identify outliers in a normal distribution. One of the methods measures the distance between a data point and the center of all data points to determine an outlier. Based on this method, the data points that do not fall within three SD of the mean are identified as outliers. However, this method is not considered appropriate because the mean and SD are statistically sensitive to the presence of outliers. Alternatively, the median and quartile range are more useful because these statistics are less sensitive to outliers. In addition, box plots can be used to identify the outliers (
Fig. 1). In this box plot, any data that lies outside the upper or lower fence lines is considered outliers.
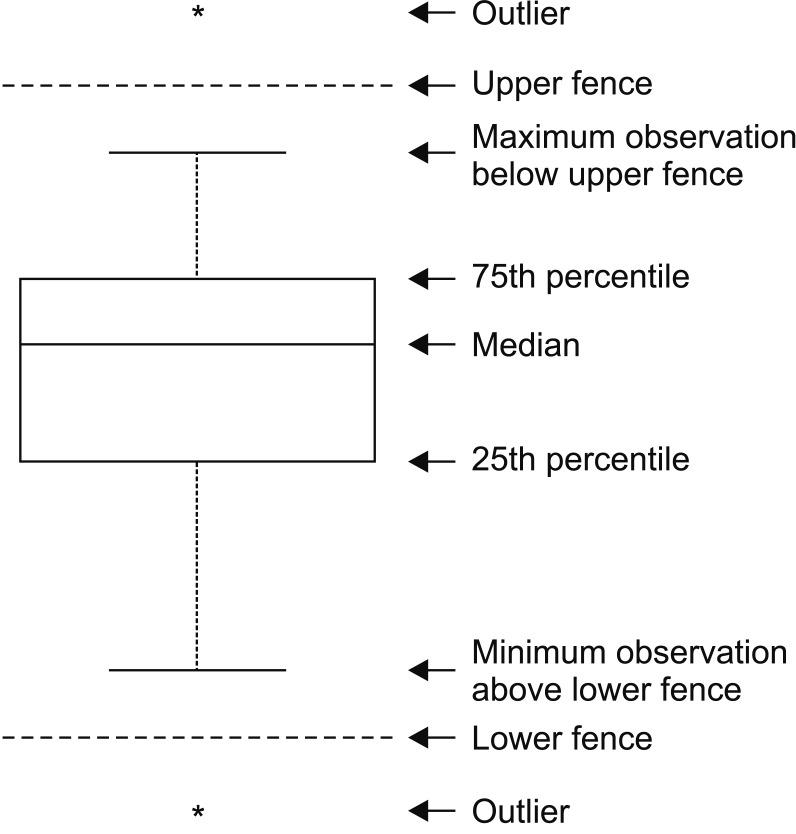 | Fig. 1Boxplot with outliers. The upper and lower fences represent values more and less than 75th and 25th percentiles (3rd and 1st quartiles), respectively, by 1.5 times the difference between the 3rd and 1st quartiles. An outlier is defined as the value above or below the upper or lower fences.
|
Many studies have explored different techniques with respect to outlier identification. Regression analysis uses simple residuals, which are adjusted by the predicted values, and standardized residuals against the observed values to detect outliers [
4]. A support vector regression is also performed for the same purpose [
5]. The need for outlier detection increases when the same kind of information is collected from different groups (K groups) or information is repeatedly collected from a single participant to ensure which groups or participant responses cause outliers. Outlier identification is also studied based on the mean and variance of each group data [
6]. In all, a simple boxplot method will be useful for determining univariate outliers. However, statistical tests that take into account the relationships between different variables are essential to detect multivariate outliers. In this review paper, we have not described each statistical testing method in detail.
Go to :

Treatment of Outliers
There are basically three methods for treating outliers in a data set. One method is to remove outliers as a means of trimming the data set. Another method involves replacing the values of outliers or reducing the influence of outliers through outlier weight adjustments. The third method is used to estimate the values of outliers using robust techniques.
Trimming
Under this approach, a data set that excludes outliers is analyzed. The trimmed estimators such as mean decrease the variance in the data and cause a bias based on under- or overestimation. Given that the outliers are also observed values, excluding them from the analysis makes this approach inadequate for the treatment of outliers.
Winsorization
This approach involves modifying the weights of outliers or replacing the values being tested for outliers with expected values. The weight modification method allows weight modification without discarding or replacing the values of outliers, limiting the influence of the outliers. The value modification method allows the replacement of the values of outliers with the largest or second smallest value in observations excluding outliers.
Robust estimation method
When the nature of the population distributions is known, this approach is considered appropriate because it produces estimators robust to outliers, and estimators are consistent. In the recent years, many studies have proposed a variety of statistical models for robust estimation; however, their applications are sluggish due to complicated methodological aspects.
Go to :

Examples of Missing Values and Outliers
This data set includes five participants and the values of the measured visual analogue scale (VAS) variable ranged from 0 to 10 (
Table 2). It is assumed that participant 5 has a missing value for the variable. When the missing value was treated in analyses of complete cases, the mean (SD) is 2.50 (1.29). The mean (SD) was then changed to 2.50 (1.12) by the mean imputation approach. It is also assumed that participant 5 had the value 99 for the variable, which falls outside the range of the measurement values (0 to 10). Therefore, it is considered a data entry error instead of an outlier. In such cases, data cleaning can be performed to track the original data and modify the abnormal value. While the mean of VAS values measured shows 3 with 1 standard deviation in a normal distribution, participant 5 is assumed to have a value of 9 for the variable; this value is larger than 6, which is the value of the mean (3) + 3 × SD (1), making it an extreme value lying outside the normal distribution. It is also an outlier resulting from participant response error. If the outlier is accounted for in the analysis, the mean (SD) would be 4.20 (2.77), which poses a problem due to the overestimation. The mean (SD) would drop to 3.00 (0.82) if the outlier is removed from the data set in accordance with the trimming method. If the winsorization method is applied by replacing the outlier with the largest or second smallest value in the data excluding the outlier, the mean (SD) would be 3.2 (0.84).
Table 2
Examples of Missing Value and Outlier
|
No. |
Data with a missing value |
Date with an outlier |
|
Raw data |
Complete case |
Imputation with the mean value |
Raw data |
Complete case |
Winsorization with the maximum value |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
2 |
2 |
2 |
2 |
2 |
2 |
2 |
|
3 |
3 |
3 |
3 |
3 |
3 |
3 |
|
4 |
4 |
4 |
4 |
4 |
4 |
4 |
|
5 |
.*
|
-†
|
2.5‡
|
9§
|
-†
|
4||
|
|
Summary |
|
N |
NA |
4 |
5 |
5 |
4 |
5 |
|
Mean |
NA |
2.50 |
2.50 |
4.20 |
3.00 |
3.2 |
|
SD |
NA |
1.29 |
1.12 |
2.77 |
0.82 |
0.84 |

Thus, the treatment of a missing value and outlier does not cause under- or over-estimation of the statistics, with neither a change in the sample size nor a bias in the results.
Go to :

Conclusions
When analyzing a data set containing missing values, the causes of missing data should be taken into account to handle the missing data properly. If a large proportion of the data is missing, further discretion is required in a manner that considers the missing rate. The use of more than one method is recommended for the handling of missing values to compare results. Furthermore, detection and treatment of outliers is important when processing collected data. Any human errors such as data entry errors should be minimized or prevented as part of the effort to reduce outliers in data. Special care is therefore necessary when entering data. This review paper underlines the efforts to minimize common problems associated with data analysis, including biased results and subsequent under- or over-estimation, by handling missing data and outliers properly during the pretreatment process.
Go to :





 PDF
PDF Citation
Citation Print
Print




 XML Download
XML Download