PDF
Citation
Print
Introduction
Statistical inference in clinical trials is a mandatory process to verify the efficacy and safety of drugs, medical devices, and procedures. It allows for generalizing the results observed through sample, so the sample by random sampling is very important. A randomized controlled trial (RCT) comparing the effects among study groups carry out to avoid any bias at the stage of the planning a study protocol. Randomization (or random allocation of subjects) can mitigate these biases with its randomness, which implies no rule or predictability for allocating subjects to treatment and control groups.
Another property of randomization is that it promotes comparability of the study groups and serves as a basis for statistical inference for quantitative evaluation of the treatment effect. Randomization can be used to create similarity of groups. In other words, all factors, whether known or unknown, that may affect the outcome can be similarly distributed among groups. This similarity is very important and allows for statistical inferences on the treatment effects. Also, it ensures that other factors except treatment do not affect the outcome. If the outcomes of the treatment group and control group show differences, this will be the only difference between the groups, leading to the conclusion that the difference is treatment induced [1].
CONSORT1), a set of guidelines proposed to improve completeness of the clinical study report, also includes randomization. Randomization plays a crucial role in increasing the quality of evidence-based studies by minimizing the selection bias that could affect the outcomes. In general, randomization places programming for random number generation, random allocation concealment for security, and a separate random code manager. After then, the generated randomization is implemented to the study [2]. Randomization is based on probability theory and hence difficult to understand. Moreover, its reproducibility problem requires the use of computer programming language. This study tries to alleviate these difficulties by enabling even a non-statistician to understand randomization for a comparative RCT design.
Methods of Randomization
The method of randomization applied must be determined at the planning stage of a study. “Randomness” cannot be predicted because it involves no rule, constraint, or characteristic. Randomization can minimize the predictability of which treatment will be performed. The method described here is called simple randomization (or complete randomization). However, the absence of rules, constraints, or characteristics does not completely eliminate imbalances by chance. For example, assume that in a multicenter study, all subjects are randomly allocated to treatment or control groups. If subjects from center A are mainly allocated to the control group and lots of subjects from center B are allocated to the treatment group, even though this is allocated with simple randomization, can we ignore the imbalance of the randomization rate in each center?
For another example, if the majority of subjects in the control group were recruited early in the study and/or the majority of those in the treatment group were recruited later in the study, can the chronological bias be ignored? The imbalance in simple randomization is often resolved through restrictive randomization, which is a slightly restricted method [3,4]. Furthermore, adaptive randomization can change the allocation of subjects to reflect the prognostic factors or the response to therapy during the study. The use of adaptive randomization has been increasing in recent times, but simple or restrictive randomization continues to be widely used [4]. In the Appendix, the R commands are prepared for the various randomization methods described below.
Simple randomization
In simple randomization, a coin or a die roll, for example, may be used to allocate subjects to a group. The best part of simple randomization is that it minimizes any bias by eliminating predictability. Furthermore, each subject can maintain complete randomness and independence with regard to the treatment administered [5]. This method is easy to understand and apply,2) but it cannot prevent the imbalances in the sample size or prognostic factors that are likely to occur as the number of subjects participating in the study decreases. If the ratio of number of subjects shows an imbalance, that is, it is not 1 : 1, even with the same number of subjects participating, the power of the study will fall. In a study involving a total of 40 subjects in two groups, if 20 subjects are allocated to each group, the power is 80%; this will be 77% for a 25/15 subject allocation and 67% for a 30/10 subject allocation (Fig. 1).3) In addition, it would be difficult to consider a 25/15 or 30/10 subject allocation as aesthetically balanced. 4) In other words, the balancing of subjects seems plausible to both researchers and readers. Unfortunately, the nature of simple randomization rarely lets the number of subjects in both groups to be equal [6]. Therefore, if it is not out of the range of the assignment ratio (e.g., 45%–55%),5) it is balanced. As the total number of subjects increases, the probability of departing from the assignment ratio, that is, the probability of imbalance, decreases. In the following, the total number of subjects and the probability of imbalance were examined in the two-group study with an assignment ratio of 45%–55% (Fig. 2). If the total number of subjects is 40, the probability of the imbalance is 52.7% (Fig. 2, point A), but this decreases to 15.7% for 200 subjects (Fig. 2, point B) and 4.6% for 400 subjects (Fig. 2, point C). This is the randomization method recommended for large-scale clinical trials, because the likelihood of imbalance in trials with a small number of subjects is high [6–8].6) However, as the number of subjects does not always increase, other solutions need to be considered. A block randomization is helpful to resolve the imbalance in number of subjects, while a stratified randomization and an adaptive randomization can help resolve the imbalance in prognostic factors.
Block randomization
If we consider only the balance in number of subjects in a study involving two treatment groups A and B, then A and B can be repeatedly allocated in a randomized block design with predefined block size. Here, a selection bias is inevitable because a researcher or subject can easily predict the allocation of the group. For a small number of subjects, their number in the treatment groups will not remain the same as the study progresses, and the statistical analysis may show the problem of poor power. To avoid this, we set blocks for randomization and balance the number of subjects in each block.7) When using blocks, we need to apply multiple blocks and randomize within each block. At the end of block randomization, the number of subjects can easily be balanced, and the maximum imbalance in the study can be limited to an appropriate level. That is, block randomization has the advantage of increasing the comparability between groups by keeping the ratio of the number of subjects between groups almost the same. However, if the block size is 2, the allocation result of the second subject in the block can be easily predicted with a high risk of observation bias.8) Therefore, the block size used should preferably be 4 or more. However, note that even when the block size is large, if the block size is known to the researcher, the risk of selection bias will increase because the treatment of the last subject in the block will be revealed. To reduce the risk of predictability from the use of one block size, the size may be varied.9)
Restricted randomization for unbalanced allocation
Sometimes unbalanced allocation becomes necessary for ethical or cost reasons [9]. Furthermore, if you expect a high dropout rate in a particular group, you have to allocate more subjects. For example, for patients with terminal cancer who are not treated with conventional anticancer agents, it would be both ethical and helpful to recruit those who would be more likely to receive a newly developed anticancer drug [10] (of course, contrary to expectations, the drug could be harmful).
As for simple randomization, the probability is first determined according to the ratio between the groups, and then the subjects are allocated. If the ratio between group A and group B is 2 : 1, the probability of group A is 2/3 and that of group B is 1/3. Block randomization often uses a jar model with a random allocation rule. To consider the method, first drop as many balls as the number of subjects into the jar according to the group allocation ratio (of course, the balls have different colors depending on the group). Whenever you allocate a subject, take out one ball randomly and confirm it, and do not place the ball back into the jar (random sampling without replacement). Repeat this allocation for each block.
Stratified randomization
Some studies have prognostic factors or covariates affecting the study outcome as well as treatment. Researchers hope to balance the prognostic factors between the study groups, but randomization does not eliminate all the imbalances in prognostic factors. Stratified randomization refers to the situation where the strata are based on level of prognostic factors or covariates. For example, if “sex” is the chosen prognostic factor, the number of strata is two (male and female), and randomization is applied to each stratum. When a male subject participates, the subject is first allocated to the male strata, and the group (treatment group, control group, etc.) is determined through randomization applied to the male strata. In a multicenter study, one typical prognostic factor is the “site.” This may be due to the differences in characteristics between the subjects and the manner and procedure in which the patients are treated in each hospital.
Stratification can reduce imbalances and increase statistical power, but it has certain problems. If several important prognostic factors affect the outcome, the number of strata would increase [11]. For example, 12 (2 × 2 × 3) strata are formed solely from recruitment hospitals (sites 1 and 2), sex (male and female), and age group (under 20 years, 20–64 years, and 65 years and older) (Fig. 3). In case of several strata in relation to the target sample size, the number of subjects allocated to a few strata may be empty or sparse. This causes an imbalance10)10) in the number of subjects allocated to the treatment group. To reduce this risk, the prognostic factors should be carefully selected. These prognostic factors should be considered again during the statistical analysis and at the end of the study.
Adaptive randomization
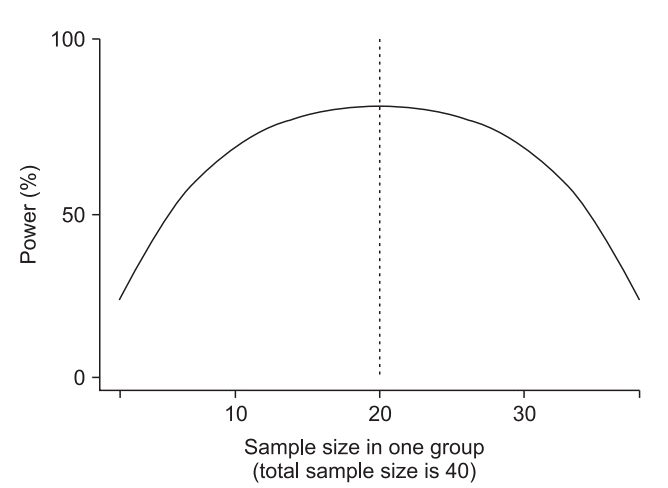
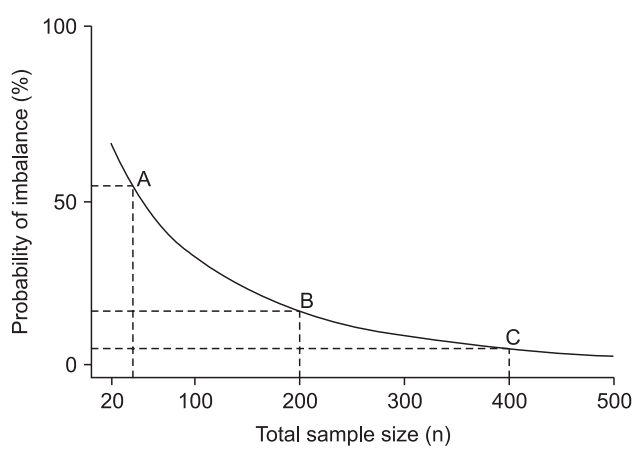
Adaptive randomization is a method of changing the allocation probability according to the progress and position of the study. It may be used to minimize the imbalance between treatment groups as well as to change the allocation probability based on the therapeutic effect. Covariate-adaptive randomization adjusts the allocation of each subject to reduce the imbalance, taking into account the imbalance of the prognostic factors. One example is the “minimization technique of randomization (minimization)” to develop indicators that collectively determine the distributional imbalance of various prognostic factors and allocates them to minimize the imbalance.
Minimization11)
Minimization was first introduced as a covariate adaptive method to balance the prognostic factors [12,13]. The first subject is allocated through simple randomization, and the subsequent ones are allocated to balance the prognostic factors. In other words, the information of the subjects who have already participated in the study is used to allocate the newly recruited subjects and minimize the imbalance of the prognostic factors [14].
Several methods have emerged following Taves [13]. Pocock and Simon define a more general method [12].12) First, the total number of imbalances is calculated after virtually allocating a newly recruited subject to all groups, respectively. Then, each group has its own the total number of imbalances. Here, this subject will be allocated to the group with lowest total number of imbalances.
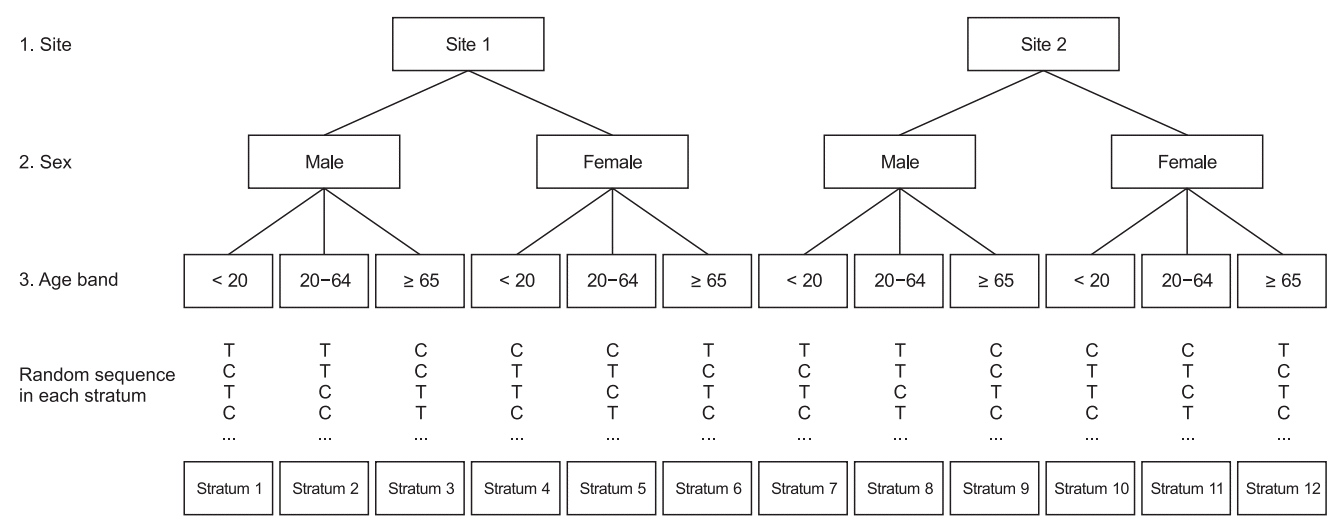
We next proceed with a virtual allocation to the recruitment hospitals (Sites 1 and 2), sex (male and female), and age band (under 20 years, 20–64 years, and 65 years or older) as prognostic factors. This study has two groups: a treatment group and a control group.
Assume that the first subject (male, 52-years-old) was recruited from Site 2. Because this subject is the first one, the allocation is determined by simple randomization.
Further, assume that the subject is allocated to a treatment group. In this group, scores are added to Site 2 of the recruiting hospital, sex Male, and the 20–64 age band (Table 1). Next, assume that the second subject (female, 25-years-old) was recruited through Site 2. Calculate the total number of imbalances when this subject is allocated to the treatment group and to the control group. Add the appropriate scores to the area within each group, and sum the differences between the areas.
First, the total number of imbalances when the subject is allocated to the control group is
The total number of imbalances when the subject is allocated to the treatment group is
Since the total number of imbalances when the subject is allocated to the control group has 1 point (< 5), the second subject is allocated to the control group, and the score is added to Site 2 of the recruiting hospital, Sex female, and the 20–64 age band in the control group (Table 2). Next, the third subject (Site 1, Sex male, 17-years-old) is recruited.
Now, the total number of imbalances when the subject is allocated to the control group is
The total number of imbalances when the subject is allocated to the treatment group is
The total number of imbalances when the subject is allocated to the control group is 2 point (< 4). Therefore, the third subject is allocated to the control group, and the score is added to Site 1 of the recruiting hospital, sex male, and the < 20 age band (Table 3). The subjects are allocated and scores added in this manner. Now, assume that the study continues, and the 15th subject (female, 74-years-old) is recruited from Site 2.
Here, the total number of imbalances when the subject is allocated to the control group is
The total number of imbalances when the subject is allocated to the treatment group is
The total number of imbalances when the subject is allocated to the control group is lower than that when the allocation is to the treatment group (3 < 5). Therefore, the 15th subject is allocated to the control group, and the score is added to Site 2 of the recruiting hospital, female sex, and the ≥ 65 age band (Table 4). If the total number of imbalances during the minimization technique is the same, the allocation is determined by simple randomization.
Although minimization is designed to overcome the disadvantages of stratified randomization, this method also has drawbacks. A concern from a statistical point of view is that it does not satisfy randomness, which is the basic assumption of statistical inference [15,16]. For this reason, the analysis of covariance or permutation test are proposed [13]. Furthermore, exposure of the subjects’ information can lead to a certain degree of allocation prediction for the next subjects. The calculation process is complicated, but can be carried out through various programs.
Response-adaptive randomization
So far, the randomization methods is assumed that the variances of treatment effects are equal in each group. Thus, the number of subjects in both groups is determined under this assumption. However, when analyzing the data accruing as the study progresses, what happens if the variance in treatment effects is not the same? In this case, would it not reduce the number of subjects initially determined rather than the statistical power? In other words, should the allocation probabilities determined prior to the study remain constant throughout the study? Alternatively, is it possible to change the allocation probability during the study by using the data accruing as the study progresses? If the treatment effects turn out to be inferior during the study, would it be advisable to reduce the number of subjects allocated to this group [17,18]?
An example of response-adaptive randomization is the randomized play-the-winner rule. Here, the first subject is allocated by predefined randomization, and if this patient’s response is “success,” the next patient will be allocated to the same treatment group; otherwise, the patient will be allocated to another treatment. That is, this method is based on statistical reasoning that is not possible under a fixed allocation probability and on the ethics of allowing more patients to be allocated to treatments that benefit the patients. However, the method can lead to imbalances between the treatment groups. In addition, if clinical studies take a very long time to obtain the results of patient responses, this method cannot be recommended.
Ethics of Randomization
As noted earlier, RCT is a scientific study design based on the probability of allocating subjects to treatment groups in order to ensure comparability, form the basis of statistical inference, and identify the effects of treatment. However, an ethical debate needs to examine whether the treatment method for the subjects, especially for patients, should be determined by probability rather than by the physician. Nonetheless, the decisions should preferably be made by probability because clinical trials have the distinct goals of investigating the efficacy and safety of new medicines, medical devices, and procedures, rather than merely reach therapeutic conclusions. The purpose of the study is therefore to maintain objectivity, which is why prejudice and bias should be excluded. That is, only an unconstrained attitude during the study can confirm that a particular medicine, medical device, or procedure is effective or safe.
Consider this from another perspective. If the researcher maintains an unconstrained attitude, and the subject receives all the information, understands it, and decides to voluntarily participate, is the clinical study ethical? Unfortunately, this is not so easy to answer. Participation in a clinical study may provide the subject with the benefit of treatment, but it could be risky. Furthermore, the subjects may be given a placebo, and not treatment. Eventually, the subject may be forced to make personal sacrifices for ambiguous benefit. In other words, some subjects have to undergo further treatment, representing the cost that society has to pay for the benefit of future subjects or for a larger number of subjects [4,19]. This ethical dilemma on the balance between individual ethics and collective ethics [20] is still spawning much controversy. If, additionally, the researcher is biased, the controversy over this dilemma will obviously become more confused and the reliability of the study will be lowered. Therefore, randomization is a key factor in a study having to clarify causality through comparison.
Conclusions
Studies have described a random table with subsequent randomization. However, if accurate information on randomization is not provided, it would be difficult to gain enough confidence to proceed with the study and arrive at conclusions. Furthermore, probability-based treatment is allowed with the hope that the trial will be conducted through proper processes, and that the outcome will ultimately benefit the medical profession. Concurrently, it should be fully appreciated that the contribution of the subjects involved in this process is a social cost.
XML Download