An overview of pharmacodynamic drug interaction with isobole and response surface model in anesthesia

병문 최

doi:10.17085/apm.2016.11.1.1

Journal List > Anesth Pain Med > v.11(1) > 1154468

Go to TopGo to Top Go to BottomGo to Bottom

TOOLS

마취영역에서 isobole과 response surface model을 이용한 약제의 상호작용 고찰

Review

Anesth Pain Med 2016;11(1):1-13.

Published online: 31 January 2016

DOI: https://doi.org/10.17085/apm.2016.11.1.1

마취영역에서 isobole과 response surface model을 이용한 약제의 상호작용 고찰

최병문

An overview of pharmacodynamic drug interaction with isobole and response surface model in anesthesia

Byung Moon Choi

Department of Anesthesiology and Pain Medicine, Asan Medical Center, University of Ulsan College of Medicine, Seoul, Korea

Corresponding author: Byung Moon Choi, M.D., Ph.D., Department of Anesthesiology and Pain Medicine, Asan Medical Center, University of Ulsan College of Medicine, 88, Olympic-ro 43-gil, Songpa-gu, Seoul 05505, Korea. Tel: 82-2-3010-1704, Fax: 82-2-3010-6790, E-mail: byungmoonchoi7@gmail.com

Received 9 November 2015 Revised 7 December 2015 Accepted 8 December 2015

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

Drug interaction is the principal concept of anesthetic practice. Typically, drug interactions are divided into three categories i.e., additive, synergistic, or infra-additive interactions. Pharmacodynamic drug interactions are typically described using mathematical models. The traditional model is an isobole, which is an iso-effect curve that shows dose or concentration combinations that result in equal effect. Response surface model is a pharmacodynamic tool that describes all isoboles and concentration effect curves for a given endpoint in one equation. In summarizing concentration-effect relationships, the response surface model allows anesthesiologists the versatility to work with precise and safe drug interactions. The aim of this review is to provide the reader with principal concepts of the isobole and response surface model and evaluate characteristics of most commonly used models, including 4 response surface models i.e., the Greco model, reduced Greco model, Minto model, and the Hierarchy model. In addition, the concept of population analysis using nonlinear mixed effects modeling is introduced.

Keywords: Drug interactions, Pharmacology

INTRODUCTION

전신마취는 의식소실(amnesia), 진통(analgesia), 근이완(muscle relaxation), 반사소실(abolition of autonomic reflex)의 4가지 요소를 필요로 하며, 이를 충족시키기 위하여 다양한 약제들이 병합 투여되고 있다. 특히 의식소실과 진통을 위하여 투여되는 수면제(hypnotics)와 아편유사제(opioid)의 경우 치료역이 좁은 약제이기 때문에 객관적인 지표에 의하여 정밀하게 적정(titration)할 필요가 있다. 이들 약제는 중추신경계에 작용하는 약제이므로 중추신경계 대리표지자를 이용하여 약제 적정의 지표로 삼을 수 있다. 특히 수면제와 아편유사제를 “적절하게 섞어서” 사용하기 위해서는 개별 약제의 약동, 약력학적 특성을 파악하는 것이 중요하다. 그렇지만 두 약제가 동시에 투여되는 상황에서는 개별 약력학은 더 이상 유효하지 않으며, 두 약제간 약력학적 상호작용의 패턴을 미리 알고 있다면 두 약제의 적정을 보다 효과적으로 할 수 있다(Fig. 1). 여기에서는 두 약제의 약동학적인 상호작용을 제외한 약력학적 상호작용의 관계를 이소볼(isobole)과 반응표면모형(response surface model)을 이용하여 탐색해 보기로 할 것이며, 이를 객관적으로 정량화해 주는 방법 중에서 유연성이 가장 뛰어난 소프트웨어인 NONMEM (nonlinear mixed effects modeling)으로 구현하는 방법까지 소개하기로 한다.

Fig. 1

Necessity for consideration of drug interaction during general anesthesia. PK: pharmacokinetic, ke0: blood-brain equilibration rate constant, PKPD: pharmacokinetic and pharmacodynamic, CNS: central nervous system.

DRUG INTERACTION

약제의 약력학적 상호작용은 크게 3가지로 분류한다. 약제가 병용 투여되는 상황에서 나타나는 효과가 개별 약제가 나타내는 효과의 합과 동일하다면 상가적(additive), 크다면 상승적(synergistic), 작다면 상가이하적(infra-additive)이라고 정의하고, 흔히 상승적을 상가이상적(supra-additive)으로, 상가이하적을 길항적(antagonistic)이라고도 부른다[1]. 이러한 약력학적 상호작용을 설명하기 위하여 상호작용 모형을 이용하는데, 이상적인 상호작용 모형의 특성을 요약하면 다음과 같다.

상호작용 모형은 이전에 수학적으로 입증된 내용과 일치해야 한다.
상호작용 모형은 약제를 노출(exposure)시키는 어떠한 방법(예: 용량, 혈장농도, 조직농도, 효과처농도)에도 동일하게 타당해야 한다.
상호작용 모형 모수(parameter)는 합리적인 크기로 정확하게 예측된 값이어야 한다.
농도반응관계에서 유연성(flexibility)을 가져야 한다. 즉, 상호작용하는 약제가 농도 반응관계의 가파름(steepness)의 정도와 최대효과가 다를 때에도, 약제의 상호작용을 설명할 수 있어야 한다.
하나, 둘 또는 세 가지 약제에 대하여 임상적인 전체 범위의 용량 혹은 농도에서 반응(response)을 예측할 수 있어야 한다.
약제가 체내에 존재하지 않을 경우에도 약제의 효과가 없다는 것을 예측할 수 있어야 한다.
상호작용 모형에서 약제 중의 한 가지가 존재하지 않을 경우에는 남아 있는 약제들에 대한 정확한 상호작용 모형으로 축소할 수 있어야 한다.

ISOBOLE

Isobole 또는 isobologram은 동일 효과를 유발하는 두 약제의 조합을 나타내어 주는 동일효과곡선(iso-effect-curve)을 말하며, 이를 Fig. 2에 제시하였다[2]. Isobole은 단지 단일 효과만을 설명하기 때문에 보편적으로 모든 경우에 적용되지는 못하지만 직관적으로 약제의 상호작용을 평가하는 데는 용이하다. 흔히 이용하는 약제의 상가적 상호작용은 Loewe 상가성(Loewe additivity)으로 표시되며 이를 식으로 표시하면 다음과 같다.

Fig. 2

Isobole. (A) additivity, (B) synergy, (C) infra-additivity. D1, and D2, are isoeffective doses of two drugs administered alone. The administration of the two drugs in combination (d1, d2) results in the same effect. If D1, and D2, are the D50 doses, in each case the line represents the 50% isobole.

식(1)

I n t e r a c t i o n i n d e x = \frac{C_{X}}{C_{50 X}} + \frac{C_{Y}}{C_{50 Y}} 〈 \begin{matrix} < 1 : s y n e r g y \\ = 1 : a d d i t i v i t y \\ > 1 : i n f r a - a d d i t i v i t y \end{matrix}

식(1)에서 C_x는 약제 X의 농도를 의미하고, C_50x는 최대 효과의 반을 나타낼 때의 약제 X의 농도를 의미하며, 이는 약제 Y에 있어서도 동일하게 적용된다. Loewe 상가성 이외에도 Bliss 독립(independence) 또는 중앙-효과 방법(median-effect method)과 같은 방법을 이용할 수는 있지만[3-5], 아직까지 Loewe 상가성이 보편적으로 이용되고 있고[6], 특히 반응표면모형의 Greco 모형에서 이를 받아들여 사용하고 있다[3].

RESPONSE SURFACE MODEL

Isobole이 특정 효과(예: 50% 효과)를 나타내는 두 약제의 조합을 나타낸 동일효과곡선이라면 반응표면모형은 두 약제의 용량 혹은 농도 조합에서 나타낼 수 있는 반응의 효과를 전체 효과 범위에서 제시한 모형이다. 통상 반응의 효과는 반응이 나타날 확률개념으로 표시를 하게 된다. 반응표면모형에서 50%의 효과를 나타낼 확률에 해당하는 두 약제의 동일효과곡선이 50% isobole이 된다(Fig. 3). 반응표면모형으로 약제의 약력학적 상호작용을 설명할 때 그림을 이용하면 이해하기가 용이하며, 대표적인 예를 Fig. 4에 제시하였다. Figs. 4A–C는 반응이 나타날 동일한 확률에서의 isobole을 이용하여 약제 상호작용을 구분할 수 있다. Fig. 4A의 경우 확률이 1일 때의 isoble이 직선임을 알 수 있기 때문에 이는 상가적 상호작용(additive interaction)을 보인다. Fig. 4B의 경우에는 확률이 1일 때의 isobole이 직선에서 0에 가까운 쪽으로 오목한(concave) 곡선의 형태를 띠게 되며, 이는 상승적 상호작용(synergistic interaction)을 의미한다. Fig. 4C의 경우에는 확률이 1일 때의 isobole이 직선에서 0에서 멀어지는 쪽으로 볼록한(convex) 곡선의 형태를 띠게 되므로, 이는 상가이하적 상호작용(infra-additive interaction)을 의미한다. Figs. 4D–F는 반응이 나타날 확률의 크기로 구분이 가능하다. Fig. 4D의 경우 한 약제의 용량 혹은 농도가 증가하면 S자 모양의 용량 반응 관계가 나오면서 최대효과까지 나오지만 다른 약제의 경우는 용량 혹은 농도를 아무리 올려도 반응이 나타날 확률이 1까지 나타나지 않는 것을 확인할 수 있다. 이는 작용제(agonist)와 부분작용제(partial agonist)의 상호작용을 설명한다. Fig. 4E의 경우는 다른 약제가 전혀 효과를 내지 않고 있으며, 작용제의 용량 혹은 농도가 증가하여도 효과를 억제하는 것을 관찰할 수 있으며, 이는 작용제와 경쟁적 길항제(competitive antagonist)의 상호작용을 설명한다. Fig. 4F의 경우는 원하는 효과가 아닌 반대의 효과가 나타나는 것을 확인할 수 있으며, 이 경우는 역작용제(inverse agonist)와 작용제의 상호작용을 설명한다. 이처럼 약제의 상호작용을 그림으로 그리면 직관적으로 파악하는 것은 용이할 수 있지만 두 약제의 상호작용의 관계를 정량화하기에는 한계가 있다. 약제의 상호작용을 설명하는 반응표면모형의 다양한 종류들을 이용하면 이들 관계들을 객관적으로 파악할 수 있다. 우선 이런 모형들을 다루는 소프트웨어인 NONMEM (nonlinear mixed effects modeling)을 간단히 소개하기로 한다.

Fig. 3

Response surface models showing synergistic (A), additive (B), and infra-additive (C) interactions. Each panel contains a response surface (upper) and an isobologram showing the 50% probability isobole (lower).

Fig. 4

Response surfaces models. For all figures, the effect with no drug is 0. (A) Additive interaction between two agonists, (B) supra-additive (synergistic) interaction between two agonists, (C) infra-additive interaction between two agonists, (D) partial agonist and full agonist; (E) competitive antagonist and full agonist, (F) inverse agonist and full agonist. The isoboles for 10, 20, 30, 40, 50, 60, 70, 80, and 90% response are shown.

NONMEM (NONLINEAR MIXED EFFECTS MODELING)

반응표면모형을 다룰 수 있는 약력분석 소프트웨어가 여러 가지가 있지만 가장 대표적이면서 최초인 것은 University of San Fransico (UCSF)의 내과의사인 Lewis Sheiner와 통계학자인 Stuart Beal이 창안한 NONMEM (nonlinear mixed effects modeling)이 있다. 사실 집단분석(population analysis) 의 개념도 이들에 의하여 최초로 제안된 것이다(Fig. 5). NONMEM은 비선형혼합효과모형(nonlinear mixed effects modeling)에서 유래된 말이면서, 동시에 집단분석용 표준 소프트웨어의 이름이기도 하다. 약력학은 S자모양 최대효과 모형(sigmoid Emax model)으로 설명하기 때문에 비선형이 대부분이라는 것을 알 수 있다. 선형회귀와 비선형 회귀는 추정 방식이 매우 다르기 때문에 이와 같이 비선형이라는 말을 강조하는 것이다. 혼합효과모형(mixed effects modeling)은 말 그대로 무엇인가가 혼합되어 있어 이들을 함께 모형화한다는 의미인데, 약동, 약력학적 모수를 집단의 평균값(이 값은 사람마다 달라지지 않으며 고정효과 모수라고 한다. NONMEM에서는 θ로 표기한다.)과 inter-individual random effects parameter로 나누는 방식을 말한다. 여기서 inter-individual random effects parameter는 random inter-individual variability를 기술해준다. 이러한 random inter-individual variability는 평균이 0이면서 분산이 ω²인 정규분포를 하는 것으로 가정한다. Random inter-individual variability는 생물학적으로 당연히 있을 수 있는 현상이며, 이 중에서 환자가 가진 특성(NONMEM에서는 이것을 covariate, 공변량이라고 부른다.)으로 설명 가능한 부분을 고정효과 모수 쪽으로 가지고 온다. 이것이 바로 집단분석의 개념이다.

Fig. 5

Concepts of population analysis using nonlinear mixed effects modeling. PK: pharmacokinetic, PD: pharmacodynamic, TCI: target-controlled infusion.

이와 같이 하려면 NONMEM의 제어구문(control code, NONMEM에게 회귀분석을 시키는 일종의 명령문의 집합) 내에 다음과 같이 적는다. 예를 들어 목표 효과처농도 조절주입에 필요한 혈액-뇌평형속도상수(k_e0)의 경우,

\begin{array}{l} TKE0 = THETA(1) \\ KE0 = TKE0*EXP(ETA(1)) \end{array}

여기서 TKE0는 k_e0의 대표값(random inter-individual variability가 0인 전형적 인간, 혹은 집단 내 평균값, 여기서는 THETA(1))이며, ETA(1)은 k_e0의 random inter-individual effects parameter이다. 즉, fixed effects parameter인 k_e0이 random inter-individual effects parameter인 ETA(1)과 지수함수를 통하여 연결되었다. 어떤 방식으로 연결하는가 하는 문제는 모형을 하는 사람이 결정할 문제이다. 곱하기나 더하기로 연결할 수도 있으며, 자료를 가장 잘 설명하는 쪽으로 선택하면 된다.

위에서 ETA(1)의 일부를 환자의 연령으로 일부 설명한다고 하자. 이 경우 NONMEM 제어구문은 다음과 같이 바꿀 수 있다.

\begin{array}{l} TKE0 = THETA(1) - THETA(2)*AGE \\ KE0 = TKE0*EXP(ETA(1)) \end{array}

위와 같은 코드가 농도, 효과 자료를 더 잘 설명하였다면, 최종 모형은 k_e0에 연령이 다음과 같이 연관된 것이 될 것이다.

TKE0 = THETA(1) - THETA(2)*AGE

위의 수식이 TCI system 안에 들어가면, 연령에 따라서 용량을 달리할 수 있게 된다. 이와 유사하게 체중, 성별 등 어떠한 약동, 약력 모수에라도 자료를 잘 설명하기만 한다면 공변량(covariate)으로 사용하여 고정효과 모수에 수학적으로 연결시킬 수 있다. 이 모든 것을 합치면 환자가 가진 모든 특성을 용량 적정에 이용할 수 있게 된다. 사실 우리가 임상에서 약물을 투여할 때 의식적이든 무의식적이든 이와 같은 방식을 취하고 있다. 다만 단편적인 지식에 근거하여 수동으로 하던 것을 정확한 수학적 모형을 바탕으로 좀 더 편리하면서도 정밀하게 컴퓨터를 이용하는 것이 다를 뿐이다. 각종 약동, 약력 모수를 고정효과(covariate 포함)와 random inter-individual variability로 설명하고도 다 설명하지 못하는 농도, 효과 곡선 부분(즉, 관찰효과와 모형 예측의 차이; observations - model predictions)은 residual random effects parameter를 사용하여 residual random variability로 넘긴다. 이 residual random variability는 효과 측정의 부정확성, 시간 표기 오류 등 실제 오차를 반영하며, 역시 평균이 0이고 분산이 σ²이라고 가정한다. 요약하면 NONMEM을 이용한 집단분석은 모수를 고정효과(공변량 포함)와 임의 개체간변이로 나누어서 환자집단의 시간-농도 혹은 농도-효과 곡선을 설명하도록 해 준다.

물론 Matlab (MathWorks, Inc., Natick, MA, USA) 또는 R (R Foundation for Statistical Computing, Vienna, Austria)과 같은 프로그램으로 반응표면모형 모수를 추정할 수 있다. 즉, 이 두 프로그램을 이용하여 아래에 제시한 각 반응표면모형의 구조모형을 이용한 제어구문을 생성할 수 있다. 그렇지만 아직까지 Matlab이나 R에서는 혼합모형에 대한 유연한 library를 제공하지 않기 때문에 모형 모수의 추정값과 그 표준편차 밖에 구하지 못하는 단점이 있다. 즉, 개인간 변이 부분에 대한 정보를 제공해 주지 못하며, 이를 설명하기 위한 공변량도 사용자가 자유롭게 제어구문에 포함시키는데 제약이 있다. 이런 단점 때문에 현재까지 마취통증의학과 영역에서 다룬 거의 대부분의 반응표면모형은 NONMEM을 이용하여 분석한 결과를 제시하고 있다.

반응표면모형 종류

Full Greco model

두 가지 약물의 상호작용을 탐색할 때 흔히 이용하는 모형으로 용량 또는 농도를 역가(potency)에 대하여 정규화(normalization)한 후에 약효(drug effect)가 각 약물의 조합(combination)을 반영하는 것으로 보고, 상승효과(synergy)를 반영하는 모수를 추가하는 것이다. 약물조합(combined drugs)의 농도는 다음과 같이 표현할 수 있다.

식(2)

C_{c o m b o} = \frac{C_{X}}{C_{50 X}} + \frac{C_{Y}}{C_{50 Y}} + α \times \frac{C_{X}}{C_{50 X}} \times \frac{C_{Y}}{C_{50 Y}}

식(2)에서 C_x는 약제 X의 농도를 의미하고, C_50x는 최대 효과의 반을 나타낼 때의 약제 X의 농도를 의미하며, 이는 약제 Y에 있어서도 동일하게 적용된다. α는 상호작용 모수이며, α가 0보다 크면 상승작용, α가 0이면 상가작용, α가 0보다 작으면 상가이하작용을 의미한다. 두 약제를 합하여 하나의 약제의 농도로 생각한 C_combo를 일반적인 억제형 sigmoid 최대효과 약력학 모형에 대입할 수 있고, 이를 반영하면 식(3)과 같다

식(3)

E f f e c t = E_{0} + (E_{m a x} - E_{0}) \times \frac{C_{c o m b o}^{γ}}{1 + C_{c o m b o}^{γ}}

여기에서 E₀는 약제가 체내에 없을 때의 기저효과이며, E_max는 약제의 최대효과, γ는 농도-반응 관계에서 직선부분의 기울기를 의미한다. 이를 NONMEM의 제어구문으로 설정하면 다음과 같다.

$INPUT ID CONX CONY RESP=DV

$PRED

EMAX = THETA(1) + EXP(ETA(1)); Maximum response

E0 = THETA(2) + EXP(ETA(2)); Baseline response

C50X = THETA(3)*EXP(ETA(3)); Concentration of drug X associated with 50% peak effect

C50Y = THETA(4)*EXP(ETA(4)); Concentration of drug Y associated with 50% peak effect

ALPH = THETA(5)*EXP(ETA(5)); Interaction term

GAM = THETA(6); Gamma

CMBO = CONX/C50X + CONY/C50Y + ALPH * CONX/ C50X * CONY/C50Y; Concentration of the combo

TY = E0 + (EMAX-E0) * (CMBO**GAM) / (1 + CMBO **GAM)

Y=TY + EPS(1); additive error model

관찰하는 효과가 연속형 자료가 아니고, 이항 자료(binary data)일 경우 로지스틱 회귀모형(logistic regression model)의 NONMEM 제어구문은 다음과 같다.

$INPUT ID CONX CONY RESP=DV

$PRED

C50X = THETA(1)*EXP(ETA(1)); Concentration of drug X associated with 50% peak effect

C50Y = THETA(2)*EXP(ETA(2)); Concentration of drug Y associated with 50% peak effect

ALPH = THETA(3)*EXP(ETA(3)); Interaction term

GAM = THETA(4); Gamma

CMBO = CONX/C50X + CONY/C50Y + ALPH * CONX/ C50X * CONY/C50Y; Concentration of the combo

P = (CMBO**GAM) / (1 + CMBO**GAM)

Y = RESP * P + (1-RESP) * (1-P)

$EST LIKELIHOOD METHOD=1 LAPLACE NOABORT

Reduced Greco model

Greco 모형은 약제 X와 Y가 모두 단일 목표 효과에 작용한다고 가정하는데, 만일 수면제(hypnotics)와 아편유사제(opioid)의 상호작용을 탐색하게 될 때 반응(response)을 수면과 관련된 지표로 보게 될 경우 아편유사제의 C₅₀이 임상적으로 사용하는 농도보다 훨씬 높게 나타나는 문제가 발생하게 된다. 이를 해결하기 위하여 축소(reduced) Greco model이 도입되었다. 약제 Y의 경우, 농도 C보다 C₅₀이 훨씬 클 경우에는 C/C₅₀은 무시할 수 있을 것이다. 따라서 약제 Y, 즉 아편유사제의 단독효과는 배제될 수 있고, 이를 식으로 표현하면 다음과 같다.

식(4)

E f f e c t = E_{0} + (E_{m a x} - E_{0}) \times \frac{{[\frac{C_{X}}{C_{50 X}} + α \times \frac{C_{X}}{C_{50 X}} \times \frac{C_{Y}}{C_{50 Y}}]}^{γ}}{1 + {[\frac{C_{X}}{C_{50 X}} + α \times \frac{C_{X}}{C_{50 X}} \times \frac{C_{Y}}{C_{50 Y}}]}^{γ}}

여기에서 모형을 축소시키는 두 가지 방법이 있는데, 첫 번째는 α와 C_50Y를 합쳐서 α’으로 치환하고, 식(4)를 다시 정리하면 다음과 같다.

식(5)

E f f e c t = E_{0} + (E_{m a x} - E_{0}) \times \frac{{[\frac{C_{X}}{C_{50 X}} \times (1 + α^{'} \times C_{Y})]}^{γ}}{1 + {[\frac{C_{X}}{C_{50 X}} \times (1 + α^{'} \times C_{Y})]}^{γ}}

여기에서 α = 1라고 가정하면 식(6)으로 축소할 수 있다.

식(6)

E f f e c t = E_{0} + (E_{m a x} - E_{0}) \times \frac{{[\frac{C_{X}}{C_{50 X}} \times (1 + \frac{C_{Y}}{C_{50 Y}})]}^{γ}}{1 + {[\frac{C_{X}}{C_{50 X}} \times (1 + \frac{C_{Y}}{C_{50 Y}})]}^{γ}}

이렇게 되면 식(6)의 C_50Y는 처음과는 다른 의미를 가지게 되는데, C_X의 효과를 두 배가 되게 함으로써 C_50X를 감소시키는데 필요한 농도가 된다. 이 축소 Greco model이 수면제와 아편유사제의 상호작용을 잘 설명해 줄 수 있는 것으로 여러 연구에서 보고되었다[7,8]. 이를 NONMEM의 제어구문으로 설정하면 다음과 같다.

$INPUT ID CONX CONY RESP=DV

$PRED

EMAX = THETA(1)+EXP(ETA(1)); Maximum response

E0 = THETA(2)+EXP(ETA(2)); Baseline response

C50X = THETA(3)*EXP(ETA(3)); Concentration of drug X associated with 50% peak effect

C50Y = THETA(4)*EXP(ETA(4)); Concentration of drug Y associated with 50% peak effect

GAM = THETA(5); Gamma

CMBO = (CONX/C50X *(1 + CONY/C50Y))**GAM/(1 + (CONX/C50X *(1+ CONY/C50Y))**GAM); concentration of the combo

TY = E0 + (EMAX-E0) * (CMBO**GAM) / (1 + CMBO **GAM)

Y=TY + EPS(1); additive error model

Minto model

Greco model이 일반적으로 많이 사용하고 있는 모형이기는 하지만 기본적으로 Greco model의 최대의 약점은 상호작용 약제들의 최대효과와 통상 Hill 계수라고 일컫는 가파름의 정도인 γ가 동일한 경우에만 적용할 수 있는 모형이라는 것이다. 이런 단점을 극복하기 위하여 Minto 등이[2] 새로운 형태의 약물상호작용 모형을 제시하였다. 먼저 각 약물의 농도를 각각의 역가(potency, C₅₀)로 나누어, 단위가 없는 표준화 농도(normalized concentration)로 변환한다.

식(7)

U_{X} = \frac{[X]}{C_{50 X}}, U_{Y} = \frac{[Y]}{C_{50 Y}} ​

두 약물의 표준화 농도의 비를 θ로 표기하면 식(8)과 같다

식(8)

θ = \frac{U_{Y}}{U_{X} + U_{Y}}

또한 두 약물의 합을 신약으로 보고 이를 U(θ)라고 하고, 역가를 U₅₀(θ)로 두자. 약물 X만 있을 경우 θ = 0, 약물 Y만 있을 경우 θ = 1이다. 즉, θ의 범위는 0과 1사이이다(0 ≤ θ ≤ 1). 두 약이 함께 투여될 경우, 약물 농도는 간단하게 U_X + U_Y이므로, 특정 비(ratio) θ에 대하여 농도-반응 관계는 식(9)로 표시가 가능하다.

식(9)

E f f e c t = E_{0} + (E_{m a x} (θ) - E_{0}) \times \frac{{(\frac{U_{X} + U_{Y}}{U_{50} (θ)})}^{γ (θ)}}{1 + {(\frac{U_{X} + U_{Y}}{U_{50} (θ)})}^{γ (θ)}}

여기에서, 특정 비 θ에서, γ(θ)는 농도-반응 곡선의 가파름(steepness)의 정도를 의미하고, U₅₀(θ)는 최대효과의 반을 나타낼 때의 단위수(number of units, U)로 역가를 뜻하며, E_max(θ)는 최대효과를 의미한다. 두 약제의 비(ratio), 즉, θ마다 E_max, C₅₀, γ가 다르며, 이는 θ마다 그 자신의 S자형 농도-반응관계(sigmoidal concentration-response relation)가 있음을 의미한다. 약물 X만 C_50X의 농도로 존재할 경우, U_X = 1, U_Y = 0, θ = 0, 약물 농도(U_X + U_Y)는 1이된다. 따라서 U₅₀(0)도 1이다. 약물 Y만 C_50Y의 농도로 존재할 경우, U_X = 0, U_Y = 1, θ = 1, 약물 농도(U_X + U_Y)는 1이다. 따라서 U₅₀(1)도 1이다.

그러므로 X든, Y든 한 약물만 C₅₀의 농도로 존재할 경우 다음과 같이 일반화할 수 있다.

식(10)

U (0, 1) = U_{X} + U_{Y} = 1

이 때의 효과는 다음과 같다.

식(11)

E = E_{0} + (E_{m a x} (0, 1) - E_{0}) \times \frac{{(\frac{1}{U_{50} (0, 1)})}^{γ (0, 1)}}{1 + {(\frac{1}{U_{50} (0, 1)})}^{γ (0, 1)}}

한 약물만 C₅₀의 농도로 존재할 경우 최대효과의 반에 해당하는 효과를 나타내게 된다.

식(12)

E = E_{0} + (E_{m a x} (0, 1) - E_{0}) \times \frac{1}{2}

따라서 식(11)과 식(12)에 의하여 식(13)이 성립한다.

식(13)

\frac{{(\frac{1}{U_{50} (0, 1)})}^{γ (0, 1)}}{1 + {(\frac{1}{U_{50} (0, 1)})}^{γ (0, 1)}} = \frac{1}{2}

따라서, U₅₀(0,1)은 1이 된다.

이번에는 각 약물이 역가 농도의 절반으로 함께 존재할 경우를 가정해 보자. 즉, U_X = 0.5, U_Y = 0.5, θ = 0.5, 약물 농도(U_X + U_Y)는 1이다.

식(14)

E = E_{0} + (E_{m a x} (0.5) - E_{0}) \times \frac{{(\frac{1}{U_{50} (0.5)})}^{γ (0.5)}}{1 + {(\frac{1}{U_{50} (0.5)})}^{γ (0.5)}}

이 경우, 약효가 최대효과의 반에 해당하는 효과보다 크다면, 상승적(synergistic)이고, 작다면 상가이하적(infra-additive)이며, 같을 경우 상가적(additive)이다. 즉, U₅₀(0.5) < 1일 경우 상승작용, U₅₀(0.5) > 1일 경우 상가이하작용, U₅₀(0.5) = 1일 경우 상가작용을 보인다.

상승작용을 보일 경우에는 최대효과의 반에 해당하는 효과보다 커야 하므로,

식(15)

\frac{{(\frac{1}{U_{50} (0.5)})}^{γ (0.5)}}{1 + {(\frac{1}{U_{50} (0.5)})}^{γ (0.5)}} > \frac{1}{2}

U₅₀(0.5) < 1이 된다.

상가이하작용을 보일 경우에는 최대효과의 반에 해당하는 효과보다 작아야 하므로,

식(16)

\frac{{(\frac{1}{U_{50} (0.5)})}^{γ (0.5)}}{1 + {(\frac{1}{U_{50} (0.5)})}^{γ (0.5)}} < \frac{1}{2}

U₅₀(0.5) > 1이 된다.

상가작용을 보일 경우에는 최대효과의 반에 해당하는 효과보다 작아야 하므로,

식(17)

\frac{{(\frac{1}{U_{50} (0.5)})}^{γ (0.5)}}{1 + {(\frac{1}{U_{50} (0.5)})}^{γ (0.5)}} = \frac{1}{2}

U₅₀(0.5) =1이 된다.

이상을 종합하면, U₅₀(θ)는 θ = 0, 1일 경우(개별 약물이 단독으로 존재할 때) 1이며, 0 < θ < 1에서 U₅₀(θ) < 1일 경우 상승작용, U₅₀(θ) > 1일 경우 상가이하작용, U₅₀(θ) = 1일 경우 상가작용을 나타낸다.

위 사항을 일반화하면 E_max(θ), U₅₀(θ), γ(θ) 함수에 대한 정보가 많지 않기 때문에 실제 상황을 경험적(empirical)으로 잘 근사할 수 있도록 4차다항식(fourth-order polynomials)을 사용해 볼 수 있다.

식(18)

f (θ) = β_{0} + β_{1} \cdot θ + β_{2} \cdot θ^{2} + β_{3} \cdot θ^{3} + β_{1} \cdot θ^{4}

약물 X만 존재할 경우(θ = 0), E_max(0) = E_maxX, U₅₀(0) = U_50X, γ(0) = γ_X이다. 또한 f(0) = β₀이다. 약물 Y만 존재할 경우(θ = 1), E_max(1) = E_maxY, U₅₀(1) = U_50Y, γ(1)= γ_Y이다. 또한 f(1) = β₀ + β₁ + β₂ + β₃ + β₄이다. 따라서, β₁ = f(1) - β₀ - β₂ - β₃ - β₄이다.

이를 이용하여 E_max(θ), γ(θ), U₅₀(θ)에 대하여 정리하면 다음과 같다.

식(19)

\begin{array}{l} E_{\max (1)} = E_{\max Y} = β_{0, E_{\max}} + β_{1, E_{\max}} + β_{2, E_{\max}} + β_{3, E_{\max}} + β_{4, E_{\max}} \\ ∴ β_{1, E_{\max}} = E_{\max Y} - β_{0, E_{\max}} - β_{2, E_{\max}} - β_{3, E_{\max}} - β_{4, E_{\max}} \\ E_{\max} (θ) = β_{0, E_{\max}} + β_{1, E_{\max}} \times θ + β_{2, E_{\max}} \times θ^{2} + β_{3, E_{\max}} \times θ^{3} + β_{4, E_{\max}} \times θ^{4} \\ β_{0, E_{\max}} = E_{\max} (0) = E_{\max X} \\ ∴ β_{1, E_{\max}} = E_{\max Y} - E_{\max X} - β_{2, E_{\max}} - β_{3, E_{\max}} - β_{4, E_{\max}} \\ ∴ E_{\max} (θ) = (E_{\max X} + (E_{\max Y} - E_{\max X} - β_{2, E_{\max}} - β_{3, E_{\max}} - β_{4, E_{\max}}) \times θ + β_{2, E_{\max}} \times θ^{2} + β_{3, E_{\max}} \times θ^{3} + β_{4, E_{\max}} \times θ^{4}) \end{array}

식(19)에서 이차항까지만 남기면 E_max(θ)는 식(20)으로 정리할 수 있다.

식(20)

E_{\max} (θ) = E_{\max X} + (E_{\max Y} - E_{\max X} - β_{2, E_{\max}}) \times θ + β_{2, E_{\max}} \times θ^{2}

식(21)

\begin{array}{l} γ (1) = γ_{Y} = β_{0, γ} + β_{1, γ} + β_{2, γ} + β_{3, γ} + β_{4, γ} \\ ∴ β_{1, γ} = γ_{Y} - β_{0, γ} - β_{2, γ} - β_{3, γ} - β_{4, γ} \\ γ (θ) = β_{0, γ} + β_{1, γ} \times θ + β_{2, γ} \times θ^{2} + β_{3, γ} \times θ^{3} + β_{4, γ} \times θ^{4} \\ β_{0, γ} = γ (0) = γ_{X} \\ ∴ γ (θ) = γ_{X} + (γ_{Y} - γ_{X} - β_{2, γ} - β_{3, γ} - β_{4, γ}) \times θ + β_{2, γ} \times θ^{2} + β_{3, γ} \times θ^{3} + β_{4, γ} \times θ^{4} \end{array}

식(21)에서 이차항까지만 남기면 γ(θ)는 식(22)로 정리할 수 있다.

식(22)

γ (θ) = γ_{X} + (γ_{Y} - γ_{X} - β_{2, γ}) \times θ + β_{2, γ} \times θ^{2}

식(23)

\begin{array}{l} U_{50} (1) = U_{50 Y} = β_{0, U_{50}} + β_{1, U_{50}} + β_{2, U_{50}} + β_{3, U_{50}} + β_{4, U_{50}} \\ ∴ β_{1,}_{U_{50}} = U_{50 Y} - β_{0, U_{50}} - β_{2, U_{50}} - β_{3, U_{50}} - β_{4, U_{50}} \\ U_{50 Y} = U_{50} (1) = 1 \\ β_{0, U_{50}} = U_{50 X} = U_{50} (0) = 1 \\ ∴ β_{1,}_{U_{50}} = - (β_{2, U_{50}} - β_{3, U_{50}} - β_{4, U_{50}}) \\ U_{50} (θ) = β_{0, U_{50}} + β_{1, U_{50}} \times θ + β_{2, U_{50}} \times θ^{2} + β_{3, U_{50}} \times θ^{3} + β_{4, U_{50}} \times θ^{4} \\ ∴ U_{50} (θ) = 1 - (β_{2, U_{50}} \times β_{3, U_{50}} \times β_{4, U_{50}}) \times θ + β_{2, U_{50}} \times θ^{2} + β_{3, U_{50}} \times θ^{3} + β_{4, U_{50}} \times θ^{4} \end{array}

식(23)에서 이차항까지만 남기면 U₅₀ (θ)는 식(24)로 정리할 수 있다.

식(24)

U_{50} (θ) = 1 - β_{2, U_{50}} \times θ + β_{2, U_{50}} \times θ^{2}

β_2,U₅₀ 이 0일 경우, 모든 θ에 대하여 U₅₀(θ) = 1이며, 이는 두 약물 간의 상호 작용이 상가작용을 의미한다. β_2,U₅₀ > 0일 경우, 0 < θ < 1에서 U₅₀ (θ) < 1이므로 상승작용을 보인다. β_2,U₅₀ < 0일 경우, 0 < θ < 1에서 U₅₀ (θ) > 1이므로 상가이하작용이다. 이는 두 약물의 최대효과가 동일함을 전제로 한다. 두 약물의 E_max와 γ가 동일하면서, 상승작용을 보일 때의 E_max(θ), γ(θ), U₅₀(θ)를 Fig. 6에 제시하였다. 두 약물의 E_max와 γ가 동일하다고 가정할 경우, NONMEM 제어구문은 다음과 같다.

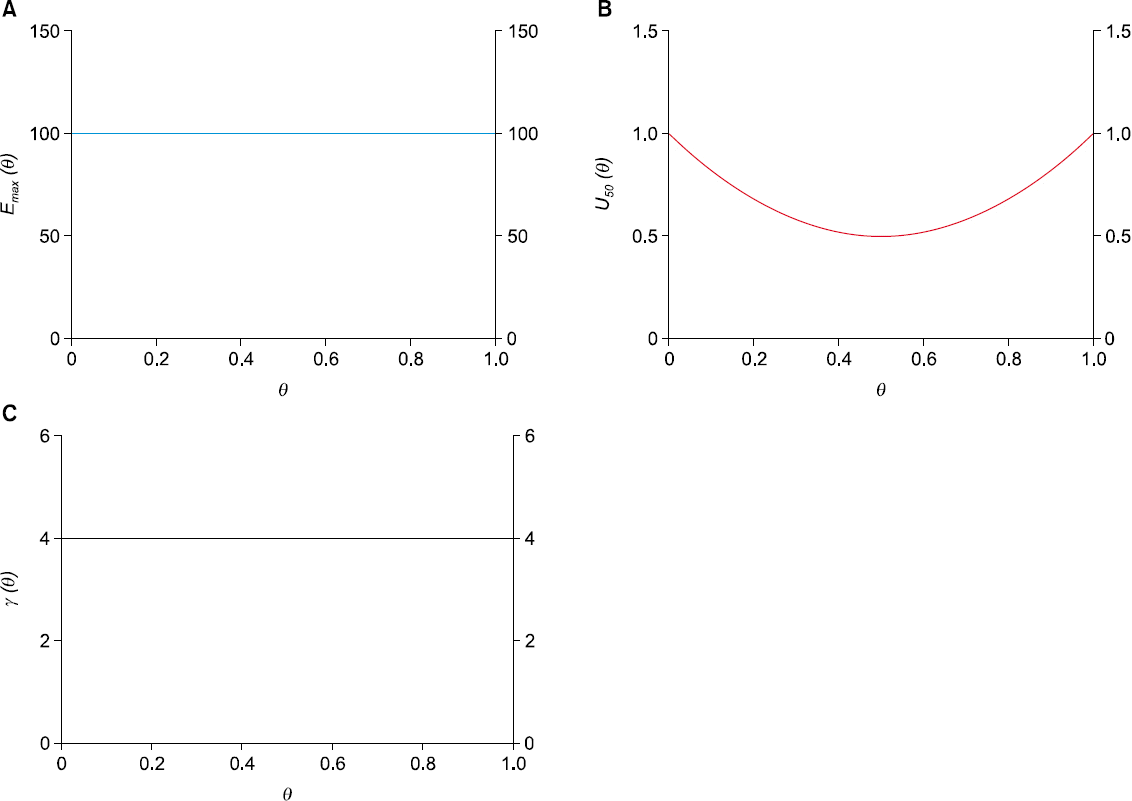Fig. 6

The functions for the parameters (Emax(θ), U50(θ), and γ(θ)) for the two drug-interaction showing synergic interaction.

$INPUT ID CONX CONY RESP=DV SEX; This example has SEX as a covariate

$PRED

C50X = THETA(1)*EXP(ETA(1))

C50Y = THETA(2)*EXP(ETA(2))

A = THETA(3)*EXP(ETA(3)); Interaction term

GAM = THETA(4)*EXP(ETA(4))

; Apply covariate effect

IF (SEX.EQ.1) THEN

C50A = C50A*THETA(5)

ENDIF

;Equations of Minto model

; Normalize to potency

UX = CONX/C50X

UY = CONY/C50Y

; Compute “theta” (Q) for Minto interaction model

IF(UX.EQ.0.AND.UY.EQ.0) THEN

Q = 0

ELSE

Q = UX/(UX + UY)

ENDIF

; Compute C50 Function In Combined Domain

U50 = 1 – A*Q + A*Q**2

; Compute “concentration” normalized to potency and corrected for interaction

U = (UX + UY)/U50

; Apply steepness term

UN = U**GAM

; Compute probability

P = UN/(1 + UN)

; Compute probability of observation

Y = RESP*P + (1 – RESP) * (1 – P)

$EST LIKELIHOOD METHOD=1 LAPLACE NOABORT

그렇지만 두 약물의 최대효과가 같지 않아도 상호작용 분석은 가능하다. 식(20), (22), (24)를 NONMEM code에 반영하여, E_maxY, E_maxX, β_2,Emax, γ_Y, γ_X, β_2,γ를 각각 추정하면 된다.

Hierarchy model

이 모형은 Kissin과 Glass가 제안한 개념을 기반으로 Bouillon 등이 제시하였다[9-11]. 모형의 수식과정에 생리적 연속성(sequence)을 상세하게 기술한 것이 특징이다. 이 모형의 가장 중요한 개념은 한 약제는 주어진 자극의 강도를 감소시키는 방향으로 작용을 하고, 또 다른 약제는 자극 강도가 감소된 상태에서 효과를 나타낸다는 것이다. 예를 들어 수면제와 아편유사제의 관계를 생각해 볼 수 있는데, 유해 자극이 환자에게 가해진다고 가정해 보자(preopioid intensity, PreOI). 아편유사제는 척수(spinal cord)에 작용하여 통증 강도를 감소시킨다(postopioid intensity, PostOI). 수면제는 척수로부터 투사되는 PostOI의 영향 하에서 대뇌피질을 억제시키게 된다. 따라서 Hill 모형의 기본 개념을 받아들여 다음과 같이 기술할 수 있다.

식(25)

E f f e c t = E_{0} + (E_{m a x} - E_{0}) \times \frac{C_{X}^{γ}}{{(C_{50 X} \times P o s t O I)}^{γ} + C_{X}^{γ}}

식(26)

P o s t O I = \Pr e O I \times [1 - \frac{C_{Y}^{γ_{Y}}}{{(C_{50 Y} \times \Pr e O I)}^{γ_{Y}} + C_{Y}^{γ_{Y}}}]

PreOI를 1이라고 가정하면 식(25)를 식(27)로 정리할 수 있고, 이것이 계층(hierarchy) 모형의 최종 수식이 된다.

식(27)

E f f e c t = E_{0} + (E_{m a x} - E_{0}) \times \frac{{(\frac{C_{X}}{C_{50 X}} \times {(1 + \frac{C_{Y}}{C_{50 Y}})}^{γ_{Y}})}^{γ}}{1 + {(\frac{C_{X}}{C_{50 X}} \times {(1 + \frac{C_{Y}}{C_{50 Y}})}^{γ_{Y}})}^{γ}}

여기에서 중요한 것은 연속적인 약제의 작용을 고려하였다는 것이다. 식(26)에서, 약제 Y가 효과를 나타내는 약제 X의 농도를 감소시키는 역할을 한다고 생각할 수 있을 것이다. 모수의 수를 감소시키기 위하여 γ_Y를 1로 고정하게 되고, 이렇게 되면 식(6)의 축소 Greco 모형과 동일하게 된다. 다양한 자극을 고려할 경우에는 모수의 개수가 증가할 것이다. Bouillon 등은[11] 과모수(overparameterization) 문제를 해결하기 위하여 수정식을 제안하였는데, 계층 모형에서 C₅₀을 비율(scaled) 또는 고정(fixed)시키자는 것이다. 이 두 경우 모두 C_50X와 C_50Y를 기본적으로 제한하게 된다. 비율(scaled) C₅₀ 계층 모형에서의 제한은 식(28)과 같이 주어진다.

식(28)

C_{50 X_{m}} = C_{50 X_{1}} \times \Pr e O I_{m}, C_{50 Y_{m}} = C_{50 Y_{1}} \times \Pr e O I_{m}

이는 다양한 자극(PreOI_m)에 대하여 PreOI를 동시에 변화시키는 것에 제한을 두고, C₅₀은 초기 C₅₀ (C_50X1, C_50Y1)으로부터 동일한 비율로 증가하는 것으로 정하게 된다.

고정(fixed) C₅₀ 계층 모형에서의 제한은 식(29)과 같이 주어진다.

식(29)

C_{50 X_{m}} = C_{50 X_{1}} \times \Pr e O I_{m}, C_{50 Y_{m}} = C_{50 Y_{1}}

C_50Y가 고정되어, 모든 자극에 대하여 동일한 것으로 간주하게 된다. 이 두 가지의 수정된 계층 모형 모두 자원자(volunteer) 연구에서 자료 적합을 잘 하는 것으로 알려져 있다[8].

반응표면모형 구축 과정에서 고려할 사항

반응표면모형을 구축할 때는 크게 3가지 접근 방법이 있다. 첫 번째로 슬라이스(slices) 방법이 있는데, 한 약제는 다양한 가성평형상태(pseudo-steady state)의 농도로 유지시키고, 다른 약제는 최대 효과의 97% 정도에 이르도록 16분 동안 영차지속정주(zero-order infusion)를 하는 방법이다. 두 번째는 열십자(crisscross) 방법으로, 연구 참여자의 반은 약제 X의 농도를 일정하게 유지한 상태에서 약제 Y의 농도를 다양하게 변화시키고, 나머지 반은 약제 Y의 농도를 일정하게 유지한 상태에서 약제 X의 농도를 다양하게 변화시킨다. 세 번째는 방사상(radial) 방법으로, 두 약제 모두를 영차지속정주한다. 그리고 각 약제를 단독 정주하고, 표면의 세 가지 방사상 슬라이스(radial slices)를 다음과 같이 취한다. 1) 개별 약제의 집단(population) C₅₀의 함수로서 동일한 정주속도를 사용한다. 2) 이 정주속도를 유지하다가 약제 X의 정주속도는 50% 감소시키고, 약제 Y의 정주속도는 50% 증가시킨다. 3) 약제 X의 정주속도는 50% 증가시키고, 약제 Y의 정주속도는 50% 감소시킨다. 이 세가지 방법 중에서 열십자 설계(crisscross design)가 가장 강건한(robust) 방법임이 밝혀졌고[12], 실제로 여러 문헌에서 이 방법으로 반응표면모형을 구축하였다[11,13]. 반응표면모형에 관한 연구는 주로 건강한 자원자를 대상으로 진행되었는데, 환자를 대상으로 하기 어려운 점이 있기 때문이다. 우선 NONMEM으로 분석할 때 개인간의 변이를 고려하려면 한 연구 참여자에게 최소 3개 이상의 농도값이 필요한데, 각 농도 값에서의 평형에 도달하는 시간이 필요하기 때문에 환자를 대상으로 진행하기에는 어려움이 있다. 두 번째로는 통상 수면제와 아편유사제의 상호작용을 탐색하는 연구들이 많은데, 수면제 없이 아편유사제 단독으로 정주해야 하는 경우에 근육강직과 같은 아편유사제의 이상반응이 나타날 수 있다. 이러한 시간적 제약과 여러 이상반응에 대한 위험을 감수하고 원하는 반응을 임상적인 용량범위에서 모두 관찰하려면 건강한 자원자를 대상으로 진행하는 것이 용이하다. 건강한 자원자를 대상으로 열십자 설계로 진행할 때에는 최소 20명 이상의 연구참여자를 모집하여야 반응표면모형을 적절하게 구축할 수 있는 것으로 알려져 있다[12].

반응표면모형의 임상적 적용

현재까지 문헌으로 소개된 반응표면모형들은 주로 약제의 평형시간(equilibration time)이 짧아서 혈장과 효과처 농도 간의 항정상태에 빨리 도달하는 약제들 위주로 연구가 되었고, sevoflurane과 remifentanil의 약력학적 상호작용[8,14-18], propofol과 remifentanil의 상호작용이 대부분을 차지하고 있다[7,11,13,19-23]. 물론 이 모형들이 실제로 어떻게 작용하는지를 다소 모호하다고 느낄 수도 있을 것이다. 우선, 동등역가비(equipotency ratio)로 약제를 대체하는데 이용할 수 있다. 사람에서 최소폐포농도(minimum alveolar concentration)를 감소시키는 것을 토대로 fentanyl, sufentanil, alfentanil, remifentanil의 역가비(potency ratio)를 계산하면 1 : 12 : 0.0625 : 1.2가 나왔다[24,25]. 이를 토대로 fentanyl의 용량에 1.2를 곱하면 remifentanil을 fentanyl로 대체하여 사용할 수 있다. 약동학 연구를 기반으로 한 다른 연구에 의하면 fentanyl, sufentanil, alfentanil, remifentanil의 역가비가 1 : 9 : 0.014 : 0.435로 계산되기도 하였다[26,27]. 또한, 각성 시간을 시뮬레이션(simulation)하는 데 반응표면모형의 결과가 이용되기도 한다. Ting 등은[18] 척추측만증(scoliosis) 수술을 받는 환자를 대상으로 수술 중 각성 검사(Stagnara wake-up test)를 시행할 때 필요한 적절한 각성 시간을 예상하기 위하여 반응표면모형을 이용하였다. Sevoflurane과 remifentanil의 반응표면모형을 이용하여 임상에서 사용하는 desflurane과 fentanyl 상호작용으로 확장하여 각성의 예측시간을 계산하였는데, 실제 환자가 각성한 시간과 반응표면모형을 이용하여 예측한 각성시간 간의 시간 차이가 평균 2.6분으로 상당히 정확하게 예측하였다[18]. 이 뿐만 아니라 반응표면모형을 이용하면 환자를 가장 빨리 각성시킬 수 있는 적절한 약제의 농도조합을 선택할 수 있는 장점도 있다.

결론

이제까지 이소볼과 반응표면모형(response surface model)의 개념과 반응표면모형의 종류 및 임상적 적용에 대하여 살펴보았다. 이소볼이 특정 효과(예: 50% 효과)를 나타내는 두 약제의 조합을 나타낸 동일효과곡선이라면 반응표면모형은 두 약제의 용량 혹은 농도 조합에서 나타낼 수 있는 반응의 효과를 전체 효과 범위에서 제시한 모형이다. 이를 잘 이해하고 있으면, 현재 임상에서 사용하는 여러 약제의 병용 투여 과정에서 약제의 세밀한 적정을 보다 효과적으로 할 수 있을 것이다.

1성별, 체중, 연령, 유전자 변이, 질환의 정도 등과 같은 환자 특이적인 공변량을 이용하여 약동, 약력 모수의 개인간 변이(inter-individual variability)를 설명하려는 분석방법. 이를 위하여 개인별 시간농도 곡선을 따로 분석하였던 standard two stage method와는 달리 모든 개체를 한꺼번에 분석함으로써 어떤 특성이 약동, 약력 모수와 연관되는지 탐색할 수 있다.

REFERENCES

1. Hendrickx JF, Eger EI 2nd, Sonner JM, Shafer SL. Is synergy the rules? A review of anesthetic interactions producing hypnosis and immobility. Anesth Analg. 2008; 107:494–506. DOI: 10.1213/ane.0b013e31817b859e. PMID: 18633028.

2. Minto CF, Schnider TW, Short TG, Gregg KM, Gentilini A, Shafer SL. Response surface model for anesthetic drug interactions. Anesthesiology. 2000; 92:1603–16. DOI: 10.1097/00000542-200006000-00017. PMID: 10839909.

3. Greco WR, Bravo G, Parsons JC. The search for synergy: a critical review from a response surface perspective. Pharmacol Rev. 1995; 47:331–85. PMID: 7568331.

4. Chou TC. Derivation and properties of Michaelis-Menten type and Hill type equations for reference ligands. J Theor Biol. 1976; 59:253–76. DOI: 10.1016/0022-5193(76)90169-7.

5. Lee SI. Drug interaction: focusing on response surface models. Korean J Anesthesiol. 2010; 58:421–34. DOI: 10.4097/kjae.2010.58.5.421. PMID: 20532049. PMCID: PMC2881515.

6. Liou JY, Tsou MY, Ting CK. Response surface models in the field of anesthesia: A crash course. Acta Anaesthesiol Taiwan. 2015; 53:139–45. DOI: 10.1016/j.aat.2015.06.005. PMID: 26321504.

7. Mertens MJ, Olofsen E, Engbers FH, Burm AG, Bovill JG, Vuyk J. Propofol reduces perioperative remifentanil requirements in a synergistic manner: response surface modeling of perioperative remifentanil-propofol interactions. Anesthesiology. 2003; 99:347–59. DOI: 10.1097/00000542-200308000-00016. PMID: 12883407.

8. Heyse B, Proost JH, Schumacher PM, Bouillon TW, Vereecke HE, Eleveld DJ, et al. Sevoflurane remifentanil interaction: comparison of different response surface models. Anesthesiology. 2012; 116:311–23. DOI: 10.1097/ALN.0b013e318242a2ec. PMID: 22222473.

9. Kissin I. General anesthetic action: an obsolete notion? Anesth Analg. 1993; 76:215–8. DOI: 10.1213/00000539-199302000-00002. PMID: 8424493.

10. Glass PS. Anesthetic drug interactions: an insight into general anesthesia--its mechanism and dosing strategies. Anesthesiology. 1998; 88:5–6. DOI: 10.1097/00000542-199801000-00004. PMID: 9447849.

11. Bouillon TW, Bruhn J, Radulescu L, Andresen C, Shafer TJ, Cohane C, et al. Pharmacodynamic interaction between propofol and remifentanil regarding hypnosis, tolerance of laryngoscopy, bispectral index, and electroencephalographic approximate entropy. Anesthesiology. 2004; 100:1353–72. DOI: 10.1097/00000542-200406000-00006. PMID: 15166553.

12. Short TG, Ho TY, Minto CF, Schnider TW, Shafer SL. Efficient trial design for eliciting a pharmacokinetic-pharmacodynamic model-based response surface describing the interaction between two intravenous anesthetic drugs. Anesthesiology. 2002; 96:400–8. DOI: 10.1097/00000542-200202000-00027. PMID: 11818774.

13. Kern SE, Xie G, White JL, Egan TD. A response surface analysis of propofol-remifentanil pharmacodynamic interaction in volunteers. Anesthesiology. 2004; 100:1373–81. DOI: 10.1097/00000542-200406000-00007. PMID: 15166554.

14. Manyam SC, Gupta DK, Johnson KB, White JL, Pace NL, Westenskow DR, et al. Opioid-volatile anesthetic synergy: a response surface model with remifentanil and sevoflurane as prototypes. Anesthesiology. 2006; 105:267–78. DOI: 10.1097/00000542-200608000-00009. PMID: 16871060.

15. Wang HL, Yang L, Guo XY, Zhang LP, Bi SS, Lu W. Response surface analysis of sevoflurane-remifentanil interactions on consciousness during anesthesia. Chin Med J (Engl). 2012; 125:2682–7.

16. Bi SS, Deng CH, Zhou TY, Guan Z, Li L, Li HQ, et al. Remifentanil-sevoflurane interaction models of circulatory response to laryngoscopy and circulatory depression. Br J Anaesth. 2013; 110:729–40. DOI: 10.1093/bja/aes504. PMID: 23388507.

17. Heyse B, Proost JH, Hannivoort LN, Eleveld DJ, Luginbuhl M, Struys MM, et al. A response surface model approach for continuous measures of hypnotic and analgesic effect during sevoflurane-remifentanil interaction: quantifying the pharmacodynamic shift evoked by stimulation. Anesthesiology. 2014; 120:1390–9. DOI: 10.1097/ALN.0000000000000180. PMID: 24566244.

18. Ting CK, Johnson KB, Teng WN, Synoid ND, Lapierre C, Yu L, et al. Response surface model predictions of wake-up time during scoliosis surgery. Anesth Analg. 2014; 118:546–53. DOI: 10.1213/ane.0000000000000094.

19. Johnson KB, Syroid ND, Gupta DK, Manyam SC, Egan TD, Huntington J, et al. An evaluation of remifentanil propofol response surfaces for loss of responsiveness, loss of response to surrogates of painful stimuli and laryngoscopy in patients undergoing elective surgery. Anesth Analg. 2008; 106:471–9. DOI: 10.1213/ane.0b013e3181606c62. PMID: 18227302. PMCID: PMC3050649.

20. LaPierre CD, Johnson KB, Randall BR, White JL, Egan TD. An exploration of remifentanil-propofol combinations that lead to a loss of response to esophageal instrumentation, a loss of responsiveness, and/or onset of intolerable ventilatory depression. Anesth Analg. 2011; 113:490–9. DOI: 10.1213/ane.0b013e318210fc45.

21. LaPierre CD, Johnson KB, Randall BR, Egan TD. A simulation study of common propofol and propofol-opioid dosing regimens for upper endoscopy: implications on the time course of recovery. Anesthesiology. 2012; 117:252–62. DOI: 10.1097/ALN.0b013e31825fb1b2. PMID: 22728781.

22. Luginbuhl M, Schumacher PM, Vuilleumier P, Vereecke H, Heyse B, Bouillon TW, et al. Noxious stimulation response index: a novel anesthetic state index based on hypnotic-opioid interaction. Anesthesiology. 2010; 112:872–80. DOI: 10.1097/ALN.0b013e3181d40368. PMID: 20216387.

23. Nieuwenhuijs DJ, Olofsen E, Romberg RR, Sarton E, Ward D, Engbers F, et al. Response surface modeling of remifentanil- propofol interaction on cardiorespiratory control and bispectral index. Anesthesiology. 2003; 98:312–22. DOI: 10.1097/00000542-200302000-00008. PMID: 12552187.

24. Glass PS, Gan TJ, Howell S, Ginsberg B. Drug interactions: volatile anesthetics and opioids. J Clin Anesth. 1997; 9(6 Suppl):S18–22. DOI: 10.1016/S0952-8180(97)00122-0.

25. McEwan AI, Smith C, Dyar O, Goodman D, Smith LR, Glass PS. Isoflurane minimum alveolar concentration reduction by fentanyl. Anesthesiology. 1993; 78:864–9. DOI: 10.1097/00000542-199305000-00009. PMID: 8489058.

26. Shafer SL, Varvel JR. Pharmacokinetics, pharmacodynamics, and rational opioid selection. Anesthesiology. 1991; 74:53–63. DOI: 10.1097/00000542-199101000-00010.

27. Egan TD, Minto CF, Hermann DJ, Barr J, Muir KT, Shafer SL. Remifentanil versus alfentanil: comparative pharmacokinetics and pharmacodynamics in healthy adult male volunteers. Anesthesiology. 1996; 84:821–33. DOI: 10.1097/00000542-199604000-00009. PMID: 8638836.

Notes

¹⁾ 성별, 체중, 연령, 유전자 변이, 질환의 정도 등과 같은 환자 특이적인 공변량을 이용하여 약동, 약력 모수의 개인간 변이 (inter-individual variability)를 설명하려는 분석방법. 이를 위하여 개인별 시간농도 곡선을 따로 분석하였던 standard two stage method와는 달리 모든 개체를 한꺼번에 분석함으로써 어떤 특성이 약동, 약력 모수와 연관되는지 탐색할 수 있다.

TOOLS

Similar articles