Abstract
To test the applicability of item response theory (IRT) to the Korean Nurses’ Licensing Examination (KNLE), item analysis was performed after testing the unidimensionality and goodness-of-fit. The results were compared with those based on classical test theory. The results of the 330-item KNLE administered to 12,024 examinees in January 2004 were analyzed. Unidimensionality was tested using DETECT and the goodness-of-fit was tested using WINSTEPS for the Rasch model and Bilog-MG for the two-parameter logistic model. Item analysis and ability estimation were done using WINSTEPS. Using DETECT, Dmax ranged from 0.1 to 0.23 for each subject. The mean square value of the infit and outfit values of all items using WINSTEPS ranged from 0.1 to 1.5, except for one item in pediatric nursing, which scored 1.53. Of the 330 items, 218 (42.7%) were misfit using the two-parameter logistic model of Bilog-MG. The correlation coefficients between the difficulty parameter using the Rasch model and the difficulty index from classical test theory ranged from 0.9039 to 0.9699. The correlation between the ability parameter using the Rasch model and the total score from classical test theory ranged from 0.9776 to 0.9984. Therefore, the results of the KNLE fit unidimensionality and goodness-of-fit for the Rasch model. The KNLE should be a good sample for analysis according to the IRT Rasch model, so further research using IRT is possible.
신규 간호사를 배출하기 위해 시행되는 간호사 자격시험, 즉 간호사 국가시험은 매년 시행되며, 시행결과 분석은 주로 고전검사이론을 기반으로 한 난이도와 분 별도, 합격률 등을 보고하고 있다. 문항분석의 난이도는 문항의 정답률로, 분별도는 상위집단과 하위집단의 정답률의 차이 또는 문항-총점간 상관관계로 계산하여 문항의 타당도를 검토하여 왔다. 이러한 기준은 일반인이나 수험생도 이해하기 쉽고, 또한 계산도 간단하다는 장점이 있다. 그러나, 고전검사이론에 의한 문항특성은 시험을 치르는 집단의 능력에 영향을 받으며, 반대로 수험생의 점수는 시험의 어렵고 쉬운 정도에 영향을 받기 때문에 능력의 측정이 안정적이지 못하다는 단점이 있다. 이러한 고전검사이론의 약점을 보완하는 것이 문항반응 이론(Item Response Theory)이다[1]. 문항반응이론에 따르면 문항마다 고유의 특성이 있어 수험생의 집단이 바뀌더라도 문항의 특성은 바뀌지 않으므로 한 문항의 특성을 파악할 수 있다면 수험생의 능력 평가를 더 정확하고 빠르게 할 수 있다는 장점이 있다. 문항반응이론에 따른 분석은 1, 0으로 표시하는 이분 모형 자료를 로지스틱모형으로 표현하는 수식 및 추정법에 대한 이해가 필요하여 현장의 교원이나 학생이 이해하기에는 쉽지 않아서 그 적용이 일반화되지 못하였으나, 요즘은 쉽게 사용할 수 있는 풀그림(program)이 많이 나와서 분석도 쉬어졌다[1].
문항반응이론은 문항특성의 불변성에 따라 도입하기 전에 몇 가지 가정이 필요하다. 일차원성 가정과 문항독립성 가정이 성립하여야 하고, 또한 자료적합성을 검토하여 문항반응이론에 적절한 자료인지를 검정하여야 한다. 이런 면에서 도입하기에 복잡한 과정이 필요하나, 이런 문항반응이론에 적절한 자료라고 판단하면 추후 문항분석이나 능력모수 추정 및 셈틀이용적응검사 (computerized adaptive testing, 이하 적응검사)에 활용할 수 있다는 장점이 있다[2]. 일차원성 가정이란, 하나의 검사(시험)는 하나의 특성을 측정한다는 것을 말한다[1]. 간호사시험은 간호사 직무수행에 필요한 능력을 측정하는 것이지 다른 여타의 능력을 측정하는 것이 개입되어서는 곤란하다. 예를 들어, 수학이나 영어의 지식이 간호사의 일상 업무에 필요한 이상의 수준으로 출제된다면 그것은 간호사 직능에 대한 시험에 다른 차원의 검사가 들어 온 것이므로 일차원이라고 볼 수가 없다. 문항독립성은 어느 한 문항이 다른 문항의 풀이에 영향을 주어서는 안된다는 것으로[1], 이전에 푼 문항이 다음문항의 답을 암시하거나 해서는 안된다. 이러한 가정은 내용적으로 검토할 수도 있지만 일차원성 가정을 검정하는 풀그림으로 사용할 수 있다. 한편, 문항반응이론이 가정하는 모형에 의해 기대되는 수험생 반응과 실제 자료에서 관찰되는 수험생 반응사이의 차이가 존재하고, 이러한 모형과 자료간의 불일치되는 정도가 커질 때는 모형이나 자료에 대한 재검토가 필요하므로 적합도(goodness-of- fit) 분석이 필요하다[3]. 적합도 분석을 통해 모형의 적합성은 물론 수험생에 대한 진단, 문항의 타당성을 확인할 수 있다. 자료의 적합성은 문항반응이론으로 분석하는 풀그림에서 제공하는 통계치로 검정한다.
이 연구에서는 여러 장점이 있는 문항반응이론을 간호사 국가시험 결과분석에 적용해보고자 한다. 새로운 검사이론의 적용 가능성을 탐색하기 위하여, 2004년도 간호사 국가시험의 수험생 응답을 자료로 하여, 문항반응이론을 도입하는 가정인 일차원성 가정 및 문항적합성을 검정하고, 고전검사 이론 및 문항반응이론에 따른 문항분석 결과의 상관관계를 알아보고자 한다. 분석 결과 간호사 국가시험자료가 문항반응이론을 적용하기에 적합하고, 문항분석과 수험생 능력추정의 결과가 기존의 고전검사이론에 따른 결과와 상관관계를 유지한다면 앞으로 문항반응이론에 의한 문항분석, 수험생 능력추정을 활성화할 수 있고 적응검사에서도 활용할 수 있을 것으로 기대한다. 이미 미국 간호사국가시험인 NCLEXRN (National Council Licensure Examination for Registered Nurses)에서는 문항반응이론의 하나인 라쉬모형(Rasch model)에 따른 적응검사를 시행하고 있다[4]. 적응검사는 문항반응이론에 의한 능력추정을 기본으로 하며, 많은 문제은행을 확보하고, 문항의 특성을 사전에 구하여야 하는 등 사전 준비가 많이 필요하나 한번 시행하면 그 후에는 경제면이나 시간 면에서 효율이 높고, 또한 수험생의 능력을 더 빠르고 정확하게 측정할 수 있다는 장점이 있다. 따라서 문항반응이론을 이용하여 문항분석을 수행하는 것은 앞으로 간호사 국가시험에서 적응시험을 시도하는 데 필요한 일이기도 하다.
연구 자료는 2004년도에 시행된 제44회 간호사국가시험의 수험생 응답자료로서, 응시자 수는 12,024명이었다. 간호사 국가시험은 8 개 과목으로 구성되어 있으며, 문항수는 간호행정 40, 성인간호 80, 기본간호 30, 아동간호 40, 지역사회 간호 40, 의료법 20, 정신간호 40, 모성간호 40으로 모두 330 문항이었다.
고전검사이론에 따른 문항분석에서 문항별 난이도는 정답률(정답을 한 응답자수/총 응답자수), 분별도는 문항-총점간 상관계수로 구하였다[5]. 일차원성 가정 분석에서는 면밀히 문항 내용을 살펴 목적에 맞는 지와 다른 문항에 영향을 줄 문항이 있는 지를 관찰하고 공분산방법인 DETECT를 이용하여 일차원성 가정을 검정하였다[6]. DETECT를 이용하여 Dmax를 구하여 0.2 미만이면 일차원성, 0.2 이상 0.4 미만이면 약한 다차원성, 0.8 이상이면 강한 다차원성으로 판정한다[6]. DETECT가 수용할 수 있는 수험생수는 6,000명이 최대이므로 6,000명을 무작위적으로 추출(random sampling)하였다. 통제 파일 설정에서 The minimum number of examinees per cell 은 20, The number of vectors to be mutated, 8, The maximum number of dimensions to run, 12로 설정하였다. 적합도 검정은 일모수 로지스틱모형인 라쉬모형에 따른 문항모수 추정 풀그림인 Winsteps 를 각 과목별로 사용하여 적합하지 않은 문항이 얼마나 있는 지 찾아보았다[7]. 문항의 적합도는 infit 과 outfit의 mean square 값이 0.5-1.5 사이면 모수 측정에 기여할 수 있는 적합한 것으로 여겼다[8]. 라쉬모형에 따른 문항모수 및 능력 모수 추과 검사정보함수 그림은 모두 Winsteps를 이용하였다. 고전검사이론 및 문항반응이론에 따른 문항모수의 상관관계 및 점수 및 능력모수의 상관관계계수는 dBSTAT 4.0을 이용하여 구하였다[9]. 각각의 과목을 또한 전체 과목을 하나의 검사로 통합한 뒤, Bilog-MG를 이용한 이모수 로지스틱모형에 따른 적합도 검정을 시도하였다[10]. Bilog-MG 실행할 때, CALIBRATION 명령어는 모두 기본 값을 사용하였다.
고전검사이론에 따른 각 과목별 평균과 표준편차는 Table 1과 같다. 100점 만점 환산한 점수는 모성간호 66.5에서 정신간호 80.8 점의 범위를 나타냈고, 문항-총점간 상관계수는 가장 낮은 지역사회간호가 0.223, 가장 높은 의료법이 0.346을 나타냈다.
일차원성 가정 검정 결과 각 과목별 Dmax는 0.10에서 0.24의 범위이었고, r 값은 0.51에서 0.68의 범위였다<Table 2>.
일모수 Rasch 모형에서 적합도 검정 결과 전 과목에서 Winsteps에서 분석한 infit 과 outfit의 mean square 값이 대부분이 0.5 와 1.5 사이지만, 아동간호에서 한 문항이 outfit mean square 값이 1.53이었다. 전체 문항대비 부적합 문항 비율은 1/330 =0.3 % 이었다. 그러나, Bilog-MG로 과목별로 이모수 로지스틱모형에 대한 적합도 검정을 시행한 결과 x2 검정에서 부적합문항은 p<0.01을 기준으로 하면 218문항이 부적합하였다(42.7%). 전체 문항을 합쳐서 부적합 문항을 보았을 때는 p<0.01을 기준으로 하면 부적합문항이 92 개이었다(27.9%).
고전검사이론의 문항 난이도(정답을 한 응답자수/총 응답자수)와 라쉬모형에 따른 문항반응이론의 난이도 지수와의 과목별 적률 상관계수는 -0.9039 에서-0.9699 사이의 값을 보였다<Table 3>. 고전검사이론에 따른 난이도의 분포를 보면 0.9 이상인 문항이 가장 많았고 그 다음 0.8~0.9 사이 순으로 난이도가 높은 것(쉬운 문항)이 많았고 낮은 문항(어려운 문항)이 적었다<Fig. 1>. 고전검사이론의 분별도를 나타내는 문항-총점간 상관계수의 분포는 0.2~03. 사이가 가장 많았다<Fig. 2>. 문항반응이론에 따른 난이도지수는 -1에서 1 까지의 문항이 가장 많아서 쉬운 문항이 많았음을 알 수 있다<Fig. 3>.
고전검사이론에 따른 수험생의 총점과 문항반응이론에 따른 수험생의 능력 모수 사이의 상관관계를 보면 라쉬모형에 따라 추정한 것은 각 과목별로 0.9852에서 0.9984로 모두 유의하게 높은 상관을 보였다<Table 4>.
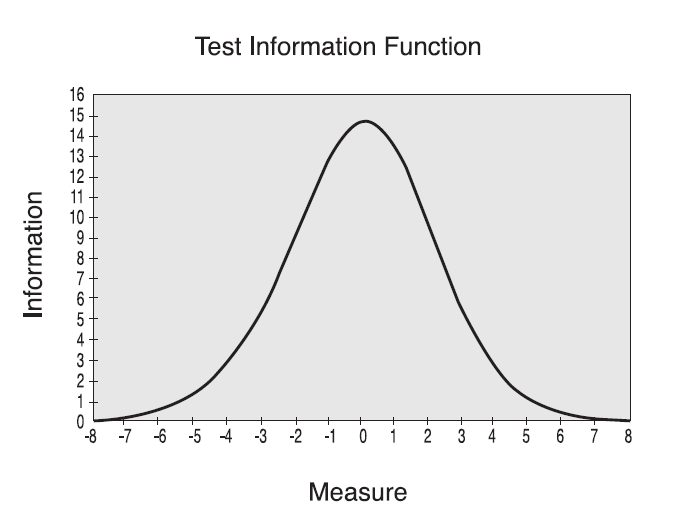
Winsteps를 이용하여 간호사 국가시험의 각 과목별 검사정보함수를 그린 결과, 검사정보함수의 형태는 모든 과목에서 유사한 모양으로 나타났는데, 검사정보함수에서 정규 분포 집단의 평균은 0.00, 표준편차를 1.00로 할 때 최대정보(Maximum information)는 수험생 능력의 평균보다 낮은 수준에서 최대값을 가지는 것으로 나타났다. 성인간호 과목의 검사정보함수를 예로 들면 최대정보함수는 <Fig. 4>와 같으며 이 과목의 수험생 능력모수의 평균은 1.14, 표준편차 0.54이었으므로 최대 정보는 능력모수 평균보다 낮은 값인 0 에서 나타났다. 다른 과목에서도 유사한 모습을 보였다.
위와 같은 결과는 간호사국가시험이 일차원성 가정을 충족하고, 또한 문항적합성이 있어 일모수 라쉬모형에 따른 문항반응이론을 도입할 수 있는 자료임을 보여준다. 의료법이 Dmax 가 0.2427 이었고 나머지는 모두 0.2. 이하로 0.1에 가까운 값을 보였다(Table 2). 일차원성 가정은 이 DETECT 이외에도 DIMTEST 등 여러 가지 방법이 있으나 모두 공분산 분석을 시도하여 공분산이 적은 것을 확인하는 작업이다.
문항 적합도는 라쉬모형에서는 INFIT 이나 OUTFIT의 mean square 값이 0.5 에서 1.5사이면 적합 문항으로 보는 데 한 문항을 제외하고는 모두 이 수치 안에 있어 대부분 적합한 것으로 볼 수 있다. 이 문항 적합도는 어느 문항이 문항반응이론 모형에 잘 부합하는지를 보여 주는 것으로 이 적합도에 맞지 않는 문항은 문항의 타당도가 의심되므로 사전에 점검하여 삭제하거나 수정하고 시행하는 것이 바람직하다. Winsteps로 산출한 라쉬모형에 의한 분석 결과에서는 부적합 문항이 한 개 발생한데 반하여, Bilog-MG로 산출한 이모수 모형에서는 42.7%이 부적합 문항으로 나왔다. 이것은 부적합한 문항의 비율이 15 % 이상이면 부적합한 문항점수가 검사점수의 타당도에 영향을 미칠수 있다는 시뮬레이션 연구결과와 비교하면 높은 비율이다[11]. 원인은 우선이 시험 문항의 변별도가 양호하지 않기 때문이거나 일반적으로 IRT 모수추정에서 난이도와 능력의 추정보다는 변별도와 추측도의 추정이 더 어렵다는 점 때문에 변별도를 고려한 모형에서 적합도가 좋지 않게 나온 것으로 추측하여 볼 수 있다[12]. 또한 Bilog-MG에서 x2 검정은 사례수가 많으면 영가설을 기각하기 쉽기 때문에 이러한 통계적 특성의 영향도 있을 것이다. 따라서 이 적합도 검정에서 Bilog-MG와 Winsteps의 차이가 단지 모형의 차이인지에 대해서는 더 연구할 필요가 있기는 하지만, 이상의 결과로부터 이 시험의 응답 자료에는 난이도만을 고려한 라쉬모형을 적용하는 것이 더 적합할 것으로 유추할 수 있다.
고전검사이론에 의한 문항모수와 문항반응이론에 의한 문항모수의 상관관계를 비교하는 것은 두 결과의 상호호환성을 알아보는데 중요한 작업이다. 고전검사이론의 문항특성과 수험생 능력이 서로 영향을 받으며 안정적이지 못하다는 단점을 가진다고는 하였으나, 이것은 사례수가 작을 때 크게 문제되는 것이지 사례수가 크고 집단의 능력분포가 다양할 때에는 변동의 정도가 크지 않다. 따라서 문항반응이론에 의한 결과가 더 정확하다 하더라도 어느 정도 유사성은 있을 것으로 예측된다. 실제로 문항의 난이도의 상관계수는 정신간호와 아동간호를 제외하고 모두 0.9 이상으로 높은 상관을 나타냈다<Table 3>. 능력모수와 점수 사이의 상관은 능력모수를 그동안 익숙하게 사용한 총점에 대체할 수 있는지를 보는 지표로, 능력모수 사용을 설명하기에 좋은 결과인데 라쉬 모형에서 추정한 능력모수와 총점은 상관이 전 과목에서 0.97 이상으로 높았다<Table 4>. 고전검사이론에 따른 문항분석 결과 난이도는 0.7 이상의 쉬운 문항이 많았다<Fig. 1>. 또한 문항-총점간 상관계수는 0.2~0.3 사이가 많아 중간 정도의 분별도를 보이는 문항이 많았다<Fig. 2>. 문항반응이론에 따른 난이도지수 분포를 살펴보면 음수의 절대값이 큰 값으로 갈수록 가장 쉬운 문항이고 양수의 큰 값으로 갈수록 어려운 문항인데, -1에서 1 까지의 문항이 다수를 차지하여 역시 쉬운 문항이 많은 것을 알 수 있었다. 난이도가 2가 넘는 어려운 문항도 32개가 있어 이 결과는 고전검사이론에서도 정답률이 매우 낮은 문항들이 존재한다는 결과와 상관이 있음을 알 수 있다<Fig. 1, 3>.
한편 흥미로운 점은 간호사 국가시험 과목을 모두 합쳐 한 과목으로 보았을 때는 문항적합도에 벗어나는 문항 수가 218개(42.7%)에서 92개(27.9%)로 감소하는 현상이었다. 이모수 로지스틱모형으로 분석할 때, 문항적합도가 라쉬모형으로 분석할 때 보다 떨어지지만 과목을 모두 합쳤을 때는 부적합 문항이 감소하는 것을 보면, 통합과목으로 간주하면 이모수 로지스틱모형의 적합성이 향상될 수도 있을 것으로 추측하며, 앞으로 이모수 로지스틱모형 또는 삼모수 로지스틱모형의 도입도 고려해볼만 하다.
검사가 어떤 능력수준의 수험생들에게 가장 오차없이 정확한 능력추정을 하는지를 알려주는 지표인 검사 정보함수는 수험생 능력이 0에서 최대값을 갖는 뾰족한 형태의 그래프로 나타나고 있는데, 수험생의 능력 모수 평균이 1.14 이므로 그 보다 낮은 점에서 최대정보함수를 보여 주므로 이는 준거참조평가(criteria-referenced examination)로서 적절한 형태의 검사정보함수의 모양이다. 이 검사가 중간보다 하위 능력의 수험생들에게 가장 잘 기능하고 있음을 보여준다<Fig. 4>.
문항반응이론은 문항의 특성과 수험생의 능력을 안정적으로 추정할 수 있다는 점에서 고전검사이론보다 나은 방법이지만, 기본적으로 이 이론을 적용하기 위해서는 충족되어야 할 가정과 자료의 적합성이 있다. 제44회 간호사 국가시험은 법규 과목에서는 충분하지 않지만 각 과목단위로 문항반응이론을 적용하기 위한 일차원성 가정을 만족하고 있으며, 일모수 라쉬모형으로 분석했을 때 문항의 적합성이 높은 것으로 나타났다. 따라서 문항반응이론에 의해 문항의 난이도, 분별도, 수험생 능력추정을 할 수 있었으며, 그 결과는 고전검사이론에 의한 결과와 높은 상관이 있으므로 매년 달라지는 문항의 정답률대신에 문항반응이론에 의한 난이도를 이 문항들의 고유한 정보로 사용하는 것이 매우 유용하고 타당한 방법이 될 수 있음을 입증하였다. 그렇다면 만약 셈틀이용적응검사를 시행하기 위해 문항모수를 사전에 문항데이터베이스에 입력하여 사용할 수도 있을 것이며, 능력모수를 이용한 합격선 설정이라든지, 시험의 난이도를 고려한 검사 동등화에도 적용될 수 있다. 앞으로 이런 문항반응이론을 간호사 국가시험에 적용할 수 있는 분야를 개발하여 시도하는 것이 어떤 교육 효과가 있고 성취도 평가에서 어떤 장단점이 있을지 알아보는 후속 연구가 필요하다.
참고문헌
1. 성 태제. 문항반응이론의 이론과 적용. 교육과학사;서울: 2001.
2. 김 영환, 손 미, 정 희태. 컴퓨터 기반 적응적 검사의 이론과 실제. 문음사;서울: 2002.
3. 지 은림, 채 선희. Rasch 모형의 이론과 실제. 교육과학사;서울: 2000.
4. National Council of State Board of Nursing. http://www.ncsbn.org/.
5. Hwang IH. The Usability of Item-Total Correlation as the Index of Item Discrimination. Korean Journal of Medical Education. 2000; 12:45–51.

6. DETECT[computer program]. http://www.assess.com/Software/DETECT.htm.
7. Winsteps. [computer program]. http://www.winsteps.com.
8. Linacre JA. A user’s guide to winsteps ministeps Rasch model computer program. Chicago, IL, U.S.A: www.winsteps.com. 2004.
9. dBSTAT version 4.0 [computer program]. http://www.dbstat.com.
10. Bilog-MG [computer program]. http://www.assess.com/.
11. Meijer. Person fit and criterion-related validity: An extension of the Schmitt, Cortina, and Whitney study. Applied Psychological Measurement. 1997; 21:99–113.
12. Van der Linden, Wim J. (EDT). Computer adaptive test; theory and practice. Kluwer Academic Publications;MA: 2000.
Fig. 1.
Distribution of the item difficulty of the 44th Korean Nurses’ License Examination (2004) based on the classical test theory.
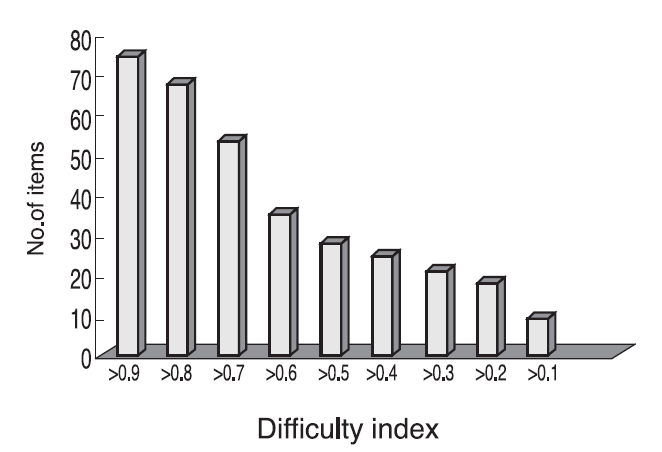
Fig. 2.
Distribution of the item total correlation in the 44th Korean Nurses’ Licensing Examination (2004) based on the classical test theory.
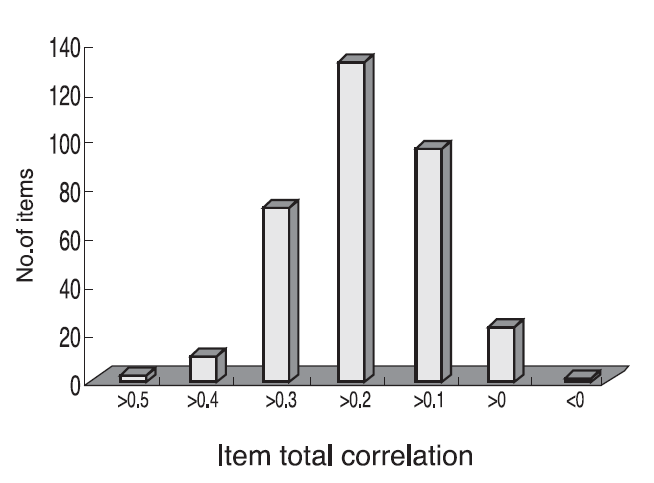
Fig. 3.
Distribution of the difficulty parameter of the 44th Korean Nurses’ License Examination (2004) based on the Rasch model item response theory estimated by Winsteps.
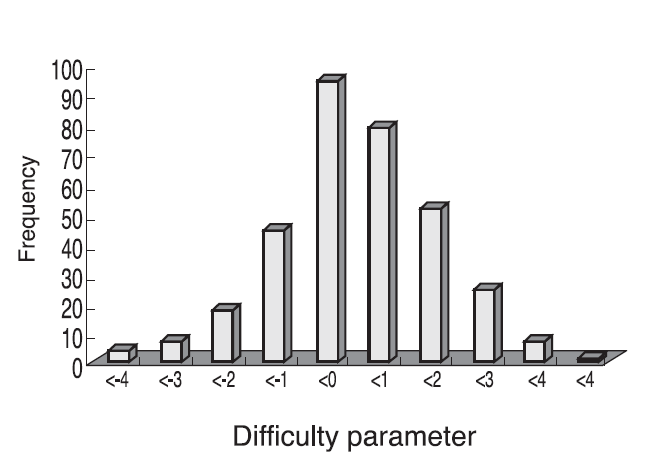
Table 1.
Mean score and item total correlation (ITC) of the Korean Nurses’ Licensing Examination in 2004
Table 2.
Unidimensionality test of the Korean Nurses’ Licensing Examination in 2004
Table 3.
Spearman’s correlation coefficients between difficulty index by classical test theory and difficulty parameter estimated by Rasch model in obtained from each subject of the Korean Nurses’ Licensing Examination in 2004
Table 4.
Pearson’s correlation coefficients between total score by classical test theory and ability parameter(theta) estimated by Rasch model obtained from each subject of the Korean Nurses’ Licensing Examination in 2004




 Citation
Citation Print
Print
 XML Download
XML Download