This article has been
cited by other articles in ScienceCentral.
Abstract
Purpose
In this study, we investigated the relationship between the noise characteristics and the number of projected images in tomosynthesis using a digital phantom.
Methods
The digital phantom consisted of a columnar phantom in the center of the image and a spherical phantom with a diameter of 80 pixels. A virtual scan was performed, and 128 projected images (Tomo_w/o) of the phantoms were obtained. The image noise according to the Poisson distribution was added to the projected images (Tomo_×1). Furthermore, another projected image with additional noise was prepared (Tomo_×1/2). For each dataset, we created datasets with 64 (half) and 32 (quarter) projections by removing the even-numbered images twice from the 128 (fully) projected images. Tomosynthesis images were reconstructed by filtered back projection (FBP). The modulation transfer function (MTF) was estimated using the sphere method, and the noise power spectrum (NPS) was estimated using the two-dimensional Fourier transform method.
Results
The MTFs did not change between datasets, and the NPSs improved as the number of projected images increased. The noise characteristics of the Tomo_×1_half images were the same as those of the Tomo_×1/2_full.
Conclusions
To achieve a reduction in the patient dose in tomosynthesis acquisition, we recommend reducing the number of projected images rather than reducing the dose per projection.
Go to :

Keywords: Tomosynthesis, Noise power spectrum, Modulation transfer function, Number of projections, Poisson distribution
Introduction
Digital tomosynthesis is a technique used to acquire three-dimensional images using a general radiography system [
1]. Many reports describe the clinical utility of the technique, and it is widely used in many fields [2–5]. The evaluation of tomosynthesis image quality has attracted considerable attention. For example, the modulation transfer function (MTF), noise power spectrum (NPS), section thickness, and focal magnification have been evaluated [
6-
9]. Breast tomosynthesis has become an indispensable technique in mammography, and there are published guidelines for the quality control of the equipment used [
10]. Tomosynthesis images are obtained by reconstructing multiple projected images taken from different angles using techniques such as filtered back projection (FBP). In this process, several parameters related to image acquisition and reconstruction affect the tomosynthesis imagery. The obtained number of projected images also affects the tomosynthesis image quality. The noise in the projected images is integrated during reconstruction; therefore, its propagation should be analyzed in particular. However, no prior studies have examined this issue in detail. In this study, the relationship between the number of projected images and the image noise was evaluated by simulation with a digital phantom.
Go to :

Materials and Methods
1. Digital phantom
In this study, we prepared a three-dimensional digital phantom for the simulation (
Fig. 1). This phantom was created in Microsoft Visual Studio Code (Microsoft Corp., Redmond, WA, USA) using Rust (a programming language). The image size was 1,024×1,024×1,024 pixels, the virtual pixel size was 0.1 mm, the background pixel value was 0, and the bit depth was 16 bits. An 800×800×100-pixel digital phantom with a pixel value of 6,000 (approximately 10% of the maximum pixel value) was placed at the center of the image. A spherical digital phantom with a diameter of 80 pixels and a pixel value set to 30,000 (approximately 50% of the maximum pixel value) was placed in the phantom to evaluate resolution characteristics. The spherical phantom lacked position dependency and could be placed anywhere; it was, therefore, placed in a corner to maximize the collection of the NPS data.
 | Fig. 1Schematic of the digital phantom. The pixel values of the columnar and spherical phantoms are 6,000 and 30,000, respectively. 
|
As shown in
Fig. 2, the digital phantom was transformed into a projected image using virtual alignment. The coordinates of the X-ray tube focal point (
fx, fy, fz
) are as shown in Eq. 1:
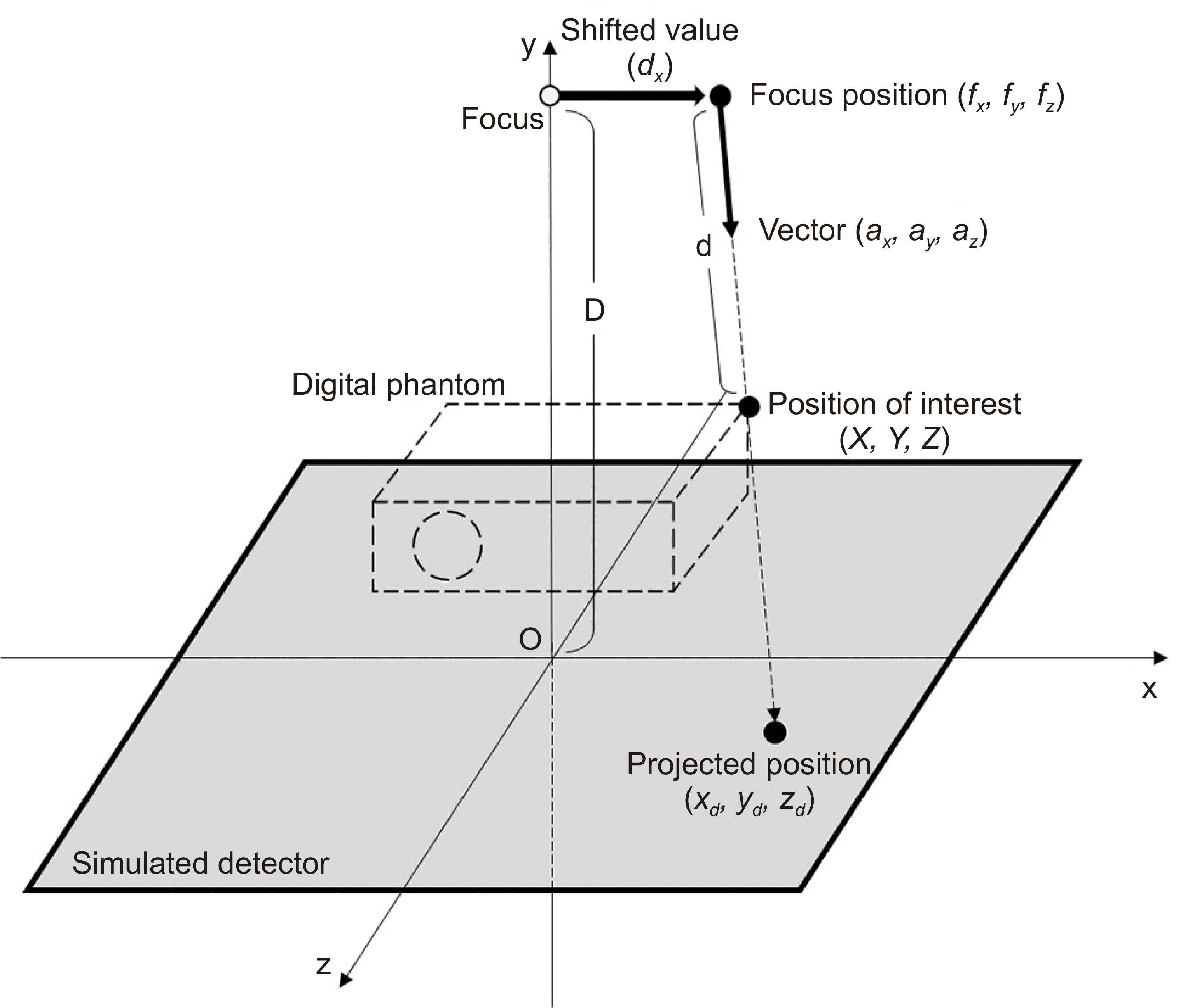 | Fig. 2Schematic of the alignment used for acquiring the projected and tomosynthesis images. 
|
where D is the length from the focus to the virtual detector and dx is the shifted value of the focus. The unit direction vector of the line (ax, ay, az
) can be expressed in terms of the coordinates of the focus and the coordinates on the virtual detector (xd, yd, zd
):
The desired coordinates (X, Y, Z) can be calculated using the following equations:
Using these equations, the projected image of the digital phantom was obtained by changing the variable t with the number of projections (
Fig. 3). In the virtual alignment,
D and the focal spot traveling distance were set to 250 and 500 pixels, respectively. As a result, the simulated angular range of the X-ray tube was ±45°, and we set the value of t to be in the range 1 to 128. We thereby obtained a digital phantom with 128 projected images with the same angular interval. The equipment with the height acquisition (e.g., Safire X-TV equipment; Shimadzu Co., Ltd., Kyoto, Japan) could collect 74 images; however, there may be equipment with a higher acquisition. Therefore, we set the maximum number of images to be collected to 128.
 | Fig. 3Angular projected images acquired when the simulated X-ray tube was positioned at ±45° and the center. 
|
2. Adding image noise
It can be assumed that the quantum motions of both the incident X-rays and the image noise follow a Poisson distribution [
11,
12]. When an event occurs exactly λ times, which, on average, occurs r times per unit time, the probability
P(r) follows a Poisson distribution defined as follows:
The projected image of the digital phantom was a noise-free image (Tomo_w/o). We prepared two datasets with different levels of image noise using Tomo_w/o. The first dataset was obtained by adding randomly generated Poisson-distributed image noise to all the projected Tomo_w/o images. The second dataset was obtained by assuming that the exposure dose was half that of the first dataset’s; this dataset was, therefore, obtained by adding the image noise twice. The first dataset was called Tomo_×1 and the second dataset Tomo_×1/2.
3. Reconstruction of the tomosynthesis image
In general, a low-pass filter is applied to tomosynthesis images to reduce artifacts in the direction of the X-ray tube movement. Therefore, in this study, a Fourier transform method and low-pass filter were applied before the back projection.
The back projection is also explained in
Fig. 2. The coordinates (
X, Y, Z) on the back-projected image are located on a straight line that passes through the position of the X-ray tube focus (
fx, fy, fz
) at a certain time, s, and the coordinates (
xd, yd, zd
) are projected onto the virtual detector. The unit vector of this line is given as follows:
where d is given by the following equation:
In addition, because the following relationship holds:
the coordinates (xd, yd, zd
) on the virtual detector are defined using yd
= 0:
Note that the vector (ax, ay, az
) is not dimensionless but has the dimensions of distance per unit time. Using the variable s, xd, and zd are given as follows:
Therefore, we calculated the coordinates of a point on a virtual detector. A two-dimensional linear interpolation was performed to obtain the reconstructed tomosynthesis image using these coordinates and the coordinates of the focal point.
Tomosynthesis reconstruction was performed on the noise-added datasets (Tomo_×1 and ×1/2) and the noise-free dataset (Tomo_w/o). The number of projected images used for the reconstruction varied for each dataset. A total of 128 projected images were generated (full projection [proj.]; Tomo_w/o full proj., _×1 full proj., and _×1/2 full proj.). We also produced a dataset that contained 64 images and excluded the even-numbered images from the full projection dataset (half projection; Tomo_w/o half proj., _×1 half proj., and _×1/2 half proj.). Finally, a 32-image dataset was created by removing the even-numbered images from the half projection dataset (quarter projection; Tomo_w/o quarter proj., _×1 quarter proj., and _×1/2 quarter proj.). Tomosynthesis reconstruction was performed for each of these datasets (
Fig. 4), meaning that a total of nine datasets were used for the analysis.
 | Fig. 4Tomosynthesis images (a) without image noise (Tomo_w/o), (b) with one-time image noise (Tomo_×1), and (c) with two-time image noise (Tomo_×1/2). 
|
4. Modulation transfer function measurement
To evaluate the effect of the added image noise and the change in the number of projected images on the resolution characteristics, the MTF was calculated using the spherical phantom (sphere method) [
13]. The one-direction MTF was estimated using only the spherical phantom because the estimation of this in the X-ray tube travel direction is difficult owing to the existence of undershoot-like artifacts. We set up a 128×20-pixel region of interest (ROI), as shown in
Fig. 5a, and obtained a profile of the pixel values. The line spread function (LSF) was obtained by differentiating this profile. In addition, the LSF was normalized using the peak value, and its base was subjected to the zeroing procedure. However, we did not perform linearization. The MTF was obtained using a one-dimensional discrete Fourier transform method of the LSF.
 | Fig. 5Region of interest (ROI) positions for (a) modulation transfer function (MTF) and (b) noise power spectrum (NPS). 
|
5. Noise power spectrum measurement
In each case, was taken as the tomosynthesis image corresponding to the middle height of the digital phantom. A 256×256-pixel ROI was extracted from the digital phantom using ImageJ (ver. 1.53; National Institutes of Health, Bethesda, MD, USA) (
Fig. 5b). Detrending was performed based on a two-dimensional polynomial fit. The NPS was estimated using the two-dimensional Fourier transform method described in a previous report [
14]. In addition, we set up a new ROI that overlapped the aforementioned ROI by 128 pixels and calculated the NPS in the same way. Finally, the NPS was calculated using 20 ROIs, and the average value of the NPS was used as the NPS of the dataset.
Go to :

Results
1. Modulation transfer function results
Fig. 6a–c show the MTF values for different numbers of projected images. The MTF values were found to be independent of the number of images.
Fig. 6d shows the MTF values with varying added image noise. There were no changes in the MTF value because of the added image noise. However, there was a slight difference in the MTF value differences, especially near 0.8 cycles/mm.
 | Fig. 6Results of the modulation transfer functions (MTFs) for (a) Tomo_w/o, (b) Tomo_×1, (c) Tomo_×1/2, and (d) different amounts of image noise. proj., projection. 
|
2. Noise power spectrum results
Fig. 7 shows the calculated NPS values of the tomosynthesis images (Tomo_w/o) without the image noise. In the vertical direction, the NPS values did not significantly change over the entire spatial frequency range. The NPS value increased as the number of projected images decreased. We found that there was an increase in the NPS values in the low-frequency region of the horizontal direction, especially as the number of projected images increased. The NPS values of the noise-added images (Tomo_×1 and ×1/2), which also increased as the number of projected images decreased, are shown in
Fig. 8. The NPS values of Tomo_×1/2 were higher than those of Tomo_×1.
Fig. 9 shows the superimposed NPS of the full and half projections for Tomo_×1 and ×1/2. In addition,
Fig. 10 shows the relationship between the number of projected images and the NPS at 2.0 cycles/mm. The NPS of the half projection for Tomo_×1 was equal to that of the full projection for Tomo_×1/2.
Fig. 11 shows the tomosynthesis images: half projection for Tomo_×1 and full projection for Tomo_×1/2. These images can be visually confirmed to contain approximately the same amount of image noise.
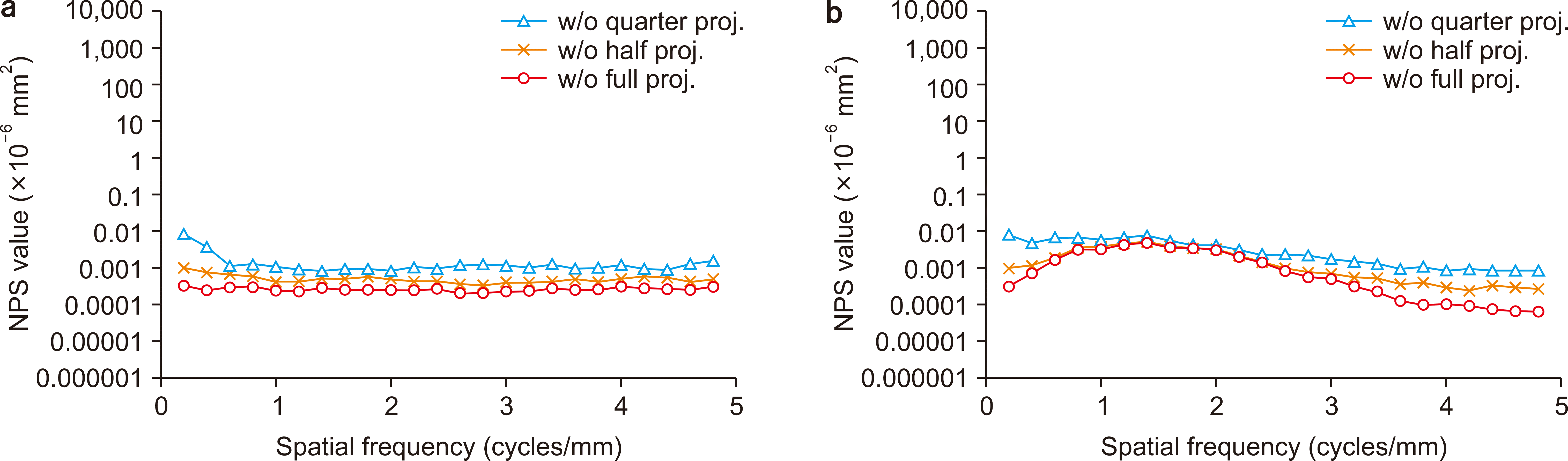 | Fig. 7Noise power spectrum (NPS) of the Tomo_w/o datasets in the (a) vertical and (b) horizontal directions. proj., projection. 
|
 | Fig. 8Noise power spectrum (NPS) of the Tomo_×1 and _×1/2 datasets in the (a) vertical and (b) horizontal directions. proj., projection. 
|
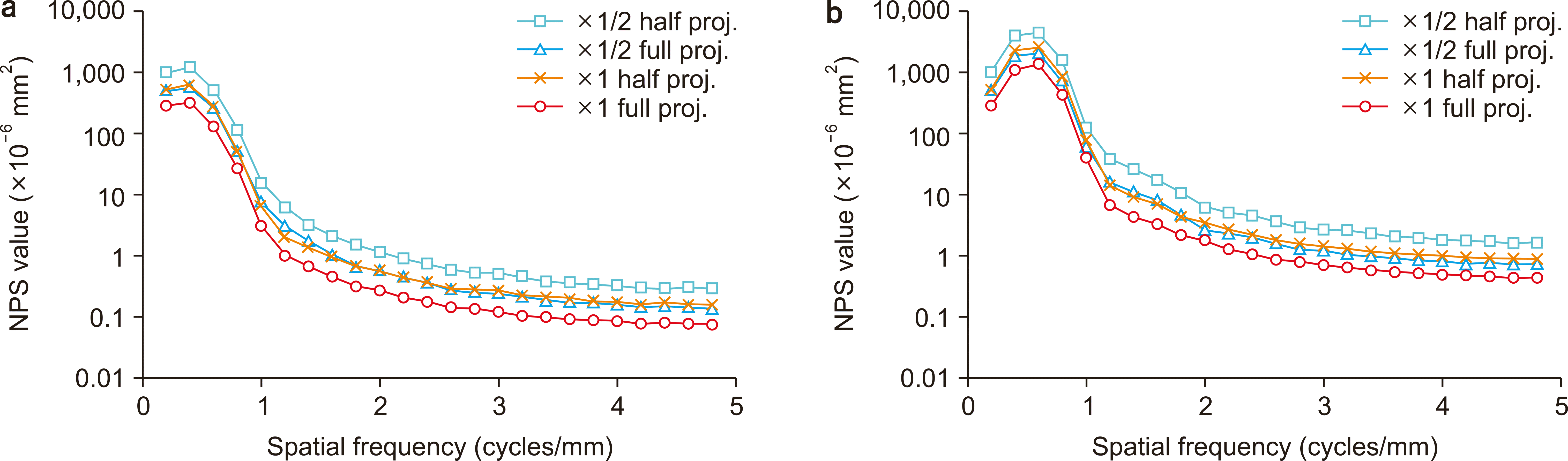 | Fig. 9Noise power spectrum (NPS) of the full and half projection of the Tomo_×1 and _×1/2 datasets in the (a) vertical and (b) horizontal directions. proj., projection. 
|
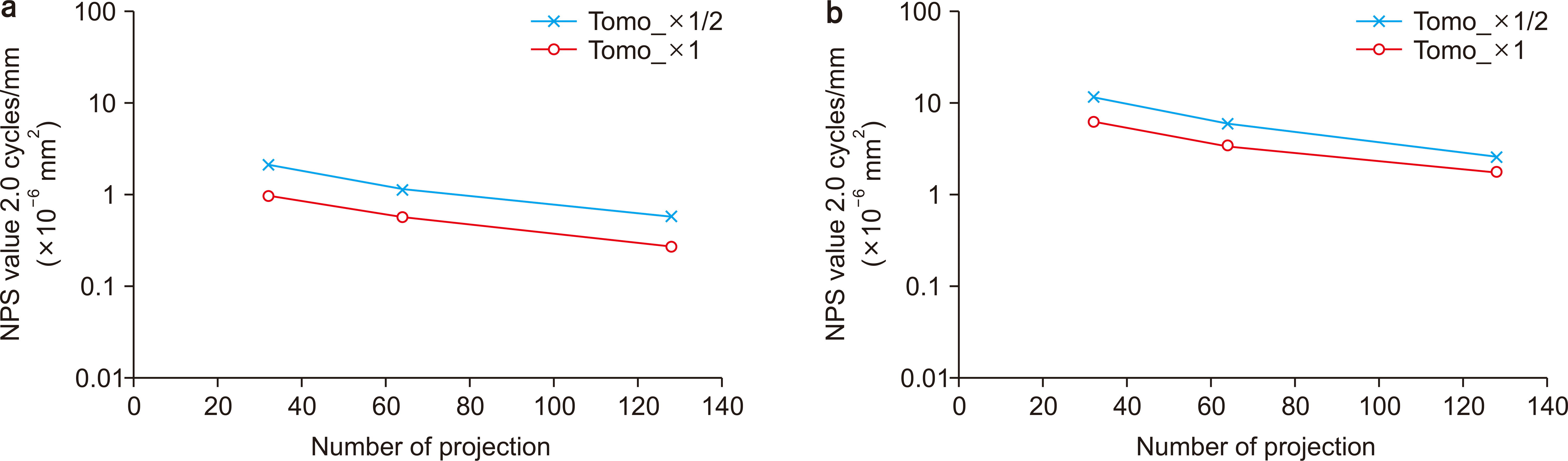 | Fig. 10Relationship between the number of projected images and the noise power spectrum (NPS) value at 2.0 cycles/mm. 
|
 | Fig. 11Samples of (a) the Tomo_×1 half projection and (b) the Tomo_×1/2 full projection. 
|
Go to :

Discussion
In many reports, real images obtained from tomosynthesis imaging equipment have been used for the evaluation of tomosynthesis image quality [
15-
17]. The use of real images is beneficial because the analysis can be directly related to the clinical equipment. However, if only specific properties are to be studied, using a digital phantom is more convenient. The advantages of the digital phantom used in this study were as follows: it was completely noise-free, an accurate spherical phantom could be prepared, and an arbitrary number of projected images could be used for reconstruction. For MTF measurement, the European Reference Organization for Quality Assured Breast Screening and Diagnostic Services (EUREF) guidelines recommend a method using a thin metal wire (wire method) [
10]. However, the wire method requires a larger exposure dose and as little image noise as possible in the direct X-ray region. In our study, the wire method was not suitable because the MTF was measured with added image noise. Therefore, we used a spherical phantom to measure the MTF. The MTF values did not change for the datasets without (Tomo_w/o) and with (Tomo_×1 and ×1/2) image noise, except for the slight difference in the MTF value at 0.8 cycles/mm. We think that these differences in the MTF value were caused by the zeroing procedure. Therefore, it was confirmed that the resolution characteristics were not degraded by the increase in image noise.
The disadvantage of the sphere method is that it involves aliasing. In the wire method, the wire is slightly angled, and multiple edge spread functions are combined to reduce the effective sampling size and suppress the aliasing effect. However, because the sphere method can obtain only profiles that are orthogonal to the spherical phantom, the effect of aliasing cannot be ignored. Therefore, the sphere method can be used only for evaluation within the same system. In this study, the MTF did not change as the number of projected images decreased. The resolution characteristics depend on the angular range when acquiring the projected image [
18]. In this study, the number of projected images was varied; however, the angular range was fixed at ±45°. It was verified that the number of projected images did not affect the MTF when the angular range was fixed.
The NPS value of Tomo_w/o was constant over the entire spatial frequency range. However, in the dataset that had an increasing number of projected images, we confirmed that the increase in the NPS values for the horizontal direction in the low-frequency region was due to the trend components that the detrending procedure could not remove. Obtaining a noise-free image is difficult because the image noise is generated by various factors in real images obtained from the tomosynthesis equipment. The digital phantom was confirmed to be suitable for our investigation. The NPS value decreased at an almost constant rate as the number of projected images increased, thus confirming that the image noise generated in the projected image was additively averaged during the reconstruction, and the amount of image noise was reduced. Simple additive averaging is evident from the results shown in
Fig. 8. The effect of image noise on the number of projected images becomes more pronounced when the number of projected images is small, such as in mammography (15–25 images). The added image noise follows a Poisson distribution over the entire image; however, it is randomly generated locally. When the image noise is added during the reconstruction, it is averaged, and the amount of image noise is reduced. In this study, as the number of projected images increased, the NPS value decreased at an almost constant rate. If the NPS value of the reference image is known, the value for the reconstructed image can easily be predicted when the exposure dose is changed. For example, as shown in
Fig. 10, the NPS value changes approximately by a factor 2.0 when the number of projected images is doubled at 2.0 cycles/mm; i.e., the change in the NPS is proportional to the number of projected images. Based on this relationship, the NPS value of the full projection of Tomo_×1/2 can be expected to be equal to that of the half projection of Tomo_×1. The results of imaging with full projection while halving the exposure dose can also be expected to be equal to those of imaging with half the number of projected images while maintaining the exposure dose. Because the MTF value does not depend on the number of projected images, the image quality can be considered to be almost the same whatever the number of the images is (
Fig. 11). In addition, most tomosynthesis imaging systems are designed to reduce the number of projected images so that the imaging can be quickly completed. If the imaging time is shorter, the effect of the movements of the patient decreases. Therefore, when considering the reduction in patient exposure, we recommend reducing the number of projected images rather than the exposure dose.
One limitation of this study is that the NPS measurement was performed on only one slice of the tomosynthesis image, which would not represent the noise characteristics of the entire dataset according to the EUREF guidelines. In this study, the characteristics of each slice did not significantly change because a digital phantom was used. However, the entire dataset should be evaluated if the data are acquired from real tomosynthesis equipment. In addition, although FBP was used in this study, tomosynthesis equipment employing iterative reconstruction is also used in clinical situations. The noise characteristics of tomosynthesis images obtained using different reconstructed methods should, therefore, also be verified.
Go to :

Conclusions
In this study, Poisson-distributed image noise was added to a digital phantom, and the relationship between the noise characteristics and the number of projected images of the reconstructed tomosynthesis images was investigated. It was found that the resolution characteristics were not affected by an increase in image noise or a decrease in the number of projected images. The noise characteristics were improved by increasing the number of projected images. To reduce patient exposure, we recommend reducing the number of projected images rather than reducing the exposure dose.
Go to :








 PDF
PDF Citation
Citation Print
Print











 XML Download
XML Download