High-Dose-Rate Electron-Beam Dosimetry Using an Advanced Markus Chamber with Improved Ion-Recombination Corrections

Dong Hyeok Jeong; Manwoo Lee; Heuijin Lim; Sang Koo Kang; Kyoung Won Jang

doi:10.14316/pmp.2020.31.4.145

Abstract

Purpose

In ionization-chamber dosimetry for high-dose-rate electron beams-above 20 mGy/pulse-the ion-recombination correction methods recommended by the International Atomic Energy Agency (IAEA) and the American Association of Physicists in Medicine (AAPM) are not appropriate, because they overestimate the correction factor. In this study, we suggest a practical ion-recombination correction method, based on Boag’s improved model, and apply it to reference dosimetry for electron beams of about 100 mGy/pulse generated from an electron linear accelerator (LINAC).

Methods

This study employed a theoretical model of the ion-collection efficiency developed by Boag and physical parameters used by Laitano et al. We recalculated the ion-recombination correction factors using two-voltage analysis and obtained an empirical fitting formula to represent the results. Next, we compared the calculated correction factors with published results for the same calculation conditions. Additionally, we performed dosimetry for electron beams from a 6 MeV electron LINAC using an Advanced Markus^® ionization chamber to determine the reference dose in water at the source-to-surface distance (SSD)=100 cm, using the correction factors obtained in this study.

Results

The values of the correction factors obtained in this work are in good agreement with the published data. The measured dose-per-pulse for electron beams at the depth of maximum dose for SSD=100 cm was 115 mGy/pulse, with a standard uncertainty of 2.4%. In contrast, the k_s values determined using the IAEA and AAPM methods are, respectively, 8.9% and 8.2% higher than our results.

Conclusions

The new method based on Boag’s improved model provides a practical method of determining the ion-recombination correction factors for high dose-per-pulse radiation beams up to about 120 mGy/pulse. This method can be applied to electron beams with even higher dose-per-pulse, subject to independent verification.

Go to :

Introduction

Typically, electron-beam radiotherapy currently utilizes two dose-rate ranges: around 1 mGy/pulse (~6 Gy/min) for conventional radiotherapy and up to about 100 mGy/pulse (~40 Gy/min) for intraoperative radiotherapy [1]. Recently, ultra-high dose rates—exceeding 200 mGy/pulse (>40 Gy/s)—have been used in pre-clinical studies for FLASH radiotherapy [2,3]. At these increased dose rates—especially at dose rates over 10 mGy/min—ion-recombination is a very significant process in dosimetry that uses an ionization chamber [4]. However, current methods for correcting for ion recombination—known as the “two-voltage technique,” which involves protocols recommended by the International Atomic Energy Agency (IAEA) or the American Association of Physicists in Medicine (AAPM)—only applies to dose rates below about 20 mGy/pulse. As pointed out in several previous works, these conventional methods overestimate the ion-recombination correction factor for high dose-per-pulse (DPP) radiation beams [5].

Boag studied the ion-recombination process theoretically since the 1950s, and he contributed to the development of the current correction methods [6]. In 1996, he published three improved models to correct for ion recombination in high-dose-rate pulsed radiation beams [6]. Currently, Boag’s models are the recognized reference standard for high-DPP radiation dosimetry. Laitano et al. [7] subsequently measured electron beams of 20–120 mGy/pulse and solved the relevant equations for Boag’s improved models. They used an iterative numerical method to determine the ion-recombination correction factors from the two measured charges (M ₁, M ₂) obtained at two polarization voltages (V ₁, V ₂) [7].

Boag’s model provides information about the ion-collection efficiency and gives a method of calculating the recombination correction factors for high-DPP beams. However, applying for practical dosimetry is inconvenient due to the difficulty of the numerical analysis. For high-DPP beams, the relationship between the DPP and the ion-recombination correction factors has been investigated using absolute dosimetry or radiochromic films, but it has not yet been applied in practice [5,8].

Through Boag’s improved model and the work of Laitano et al. [7] cited above, ion-recombination correction factors can be determined directly in terms of the one variable, M ₁/M ₂, as in the conventional two-voltage technique, but without requiring iterative methods. In the present study, by reconstructing these calculated results, we developed a fitting formula that yields the ion-recombination correction factor using only two measured values. This fitting formula exhibits a similar shape to those provided by the TRS-398 or TG-51 protocols, and it is useful for practical applications. We verified the results by recalculating the ion-recombination correction factors published by Laitano et al. [7]. Then, we applied this method to determine the reference dose rate for electron beams generated by an electron linear accelerator (LINAC). We used the Advanced Markus^® plane-parallel ionization chamber (PTW, Freiburg, Germany) with 1 mm electrode spacing throughout this study [9].

Go to :

Materials and Methods

1. Ion-recombination correction

The ion-recombination correction factor is used to correct the response of an ionization chamber for the lack of complete charge collection, which is due to the recombination of ions exhibiting opposite charges during transit to each electrode. For positive ions, the ion-collection efficiency f is given by the ratio of the collected charge M to the total charge produced, M₀: f=M/M₀. Then, the ion-recombination correction factor is defined as k_s=1/f [6,10].

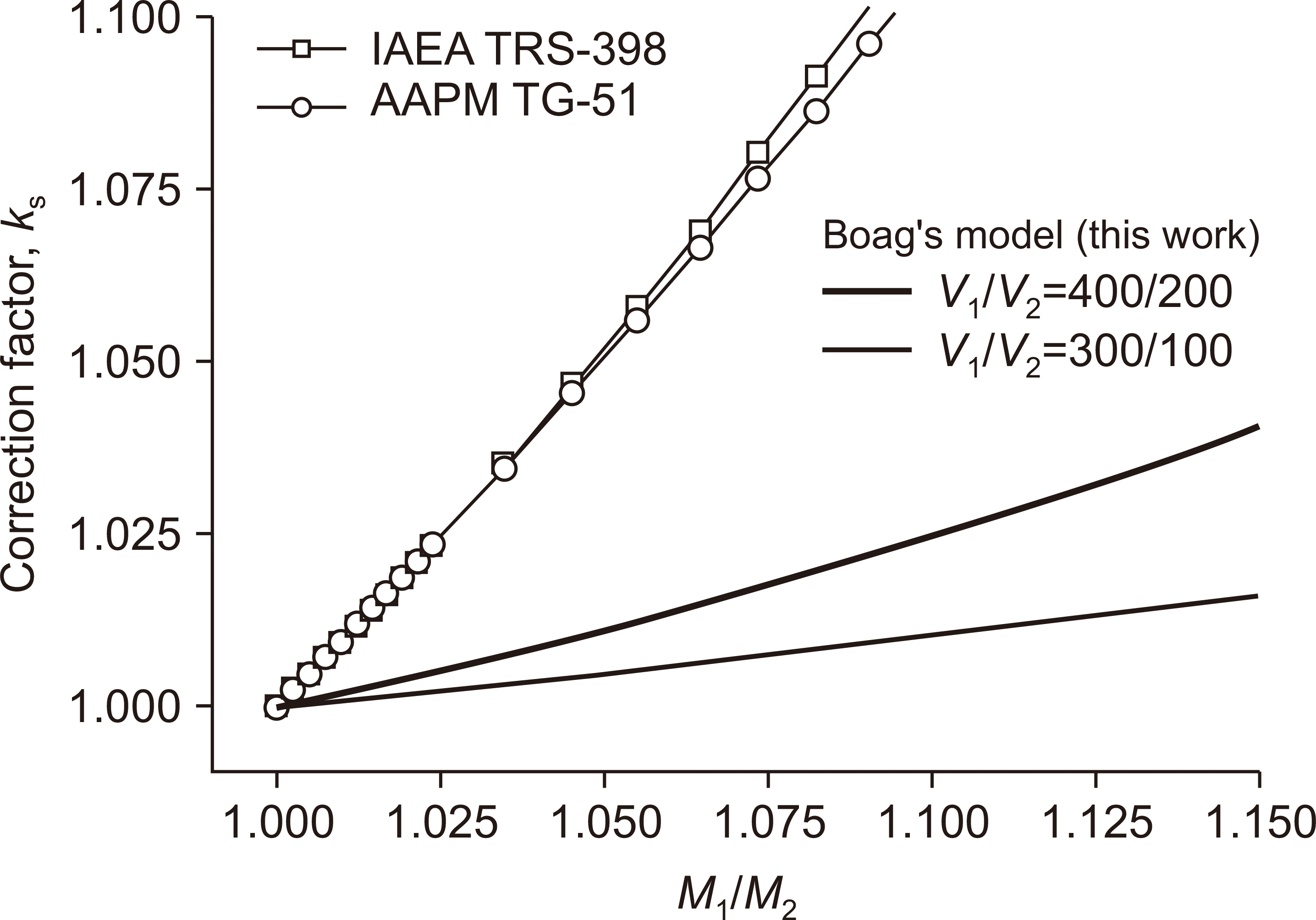
Because interactions between the ions themselves—or between ions and neutral molecules—in an electric field are complicated, determining f or k_s exactly is difficult, so k_s is currently obtained from empirical formulas [10]. In the IAEA code of practice (the TRS-398 protocol) for pulsed radiation beams, the ion-recombination correction factor k_s is given by [11]

(1)

$k_{s} {=a}_{0} {+a}_{1} (\frac{M_{1}}{M_{2}}) {+a}_{2} {(\frac{M_{1}}{M_{2}})}^{2},$

where a₀, a₁, and a₂ are constants that depend on the ratio V₁/V₂ of the two polarizing voltages. For V₁/V₂=2, the values of the constants are a₀=2.337, a₁=–3.636, and a₂=2.229. The quantity M₁/M₂ is the ratio of the charges measured at the two polarizing voltages V₁ and V₂. Similarly, in the AAPM TG-51 protocol, the ion-recombination correction factor P_ion (=k_s) is given by [12]

(2)

$P_{ion} = (\frac{1 - V_{1} / V_{2}}{M_{1} / M_{2} - V_{1} / V_{2}}) .$

Both of these methods are based on Boag’s early model (1950), which assumes a linear dependence of 1/M on 1/V [11]. According to that model, the correction factor is determined by extrapolating the 1/M vs. 1/V plot to determine the value 1/M₀ obtained when 1/V=0, where M₀ is the saturated charge for which f=1. By estimating M₀, one can thus obtain the ion-correction efficiency f=M₁/M₀ or the ion-recombination correction factor k_s=M₀/M₁ [13].

The quantity f declines from 1 to 0 with increasing DPP, and for clinical electron beams (DPP<1 mGy), the recombination correction factor can be determined using the current methods that apply the dosimetry protocols of the IAEA and AAPM. However, because free electrons that do not contribute to the production of negative ions increase with increasing DPP, eventually the value of f does not continue to decrease significantly. Thus, the current methods are not appropriate for cases with high DPP, especially DPP>20 mGy [6,7].

Therefore, in order to incorporate free electrons into the determination of the ion-collection efficiency, Boag proposed three improved models, where the third model (denoted by f''') was introduced as a practical correction method for high-DPP electron beams [6]. The ion collection efficiency (f’’’) in Boag’s third model is given by [6]

(3)

$f''= λ + \frac{1}{u} ln [1 + \frac{e^{λ (1 - λ)u} - 1}{λ}],$

where

$λ = 1 \sqrt{1 - p}$ , p is the free-electron fraction of the total electrons produced by a beam pulse, the dimensionless parameter u=µrd²/V, where µ depends on the ionic recombination coefficient and the ion mobility, r is the charge density of positive ions initially generated by the beam pulse, d is the electrode spacing, and V is the polarizing voltage [6,7].

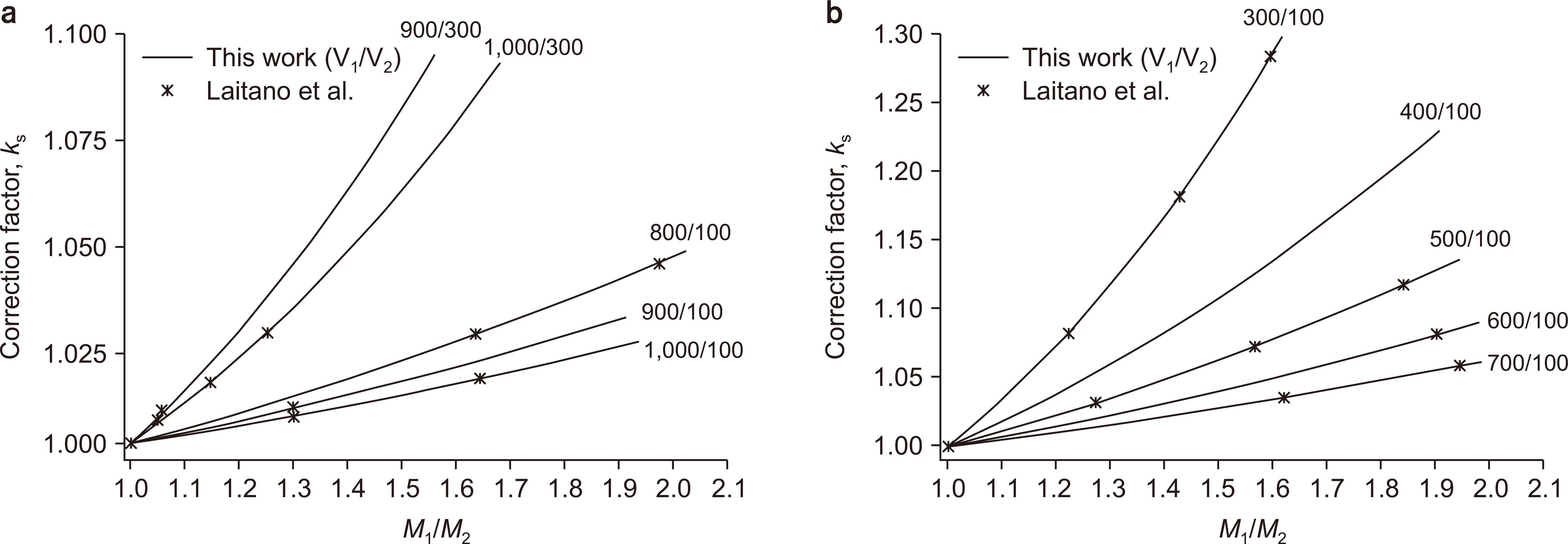
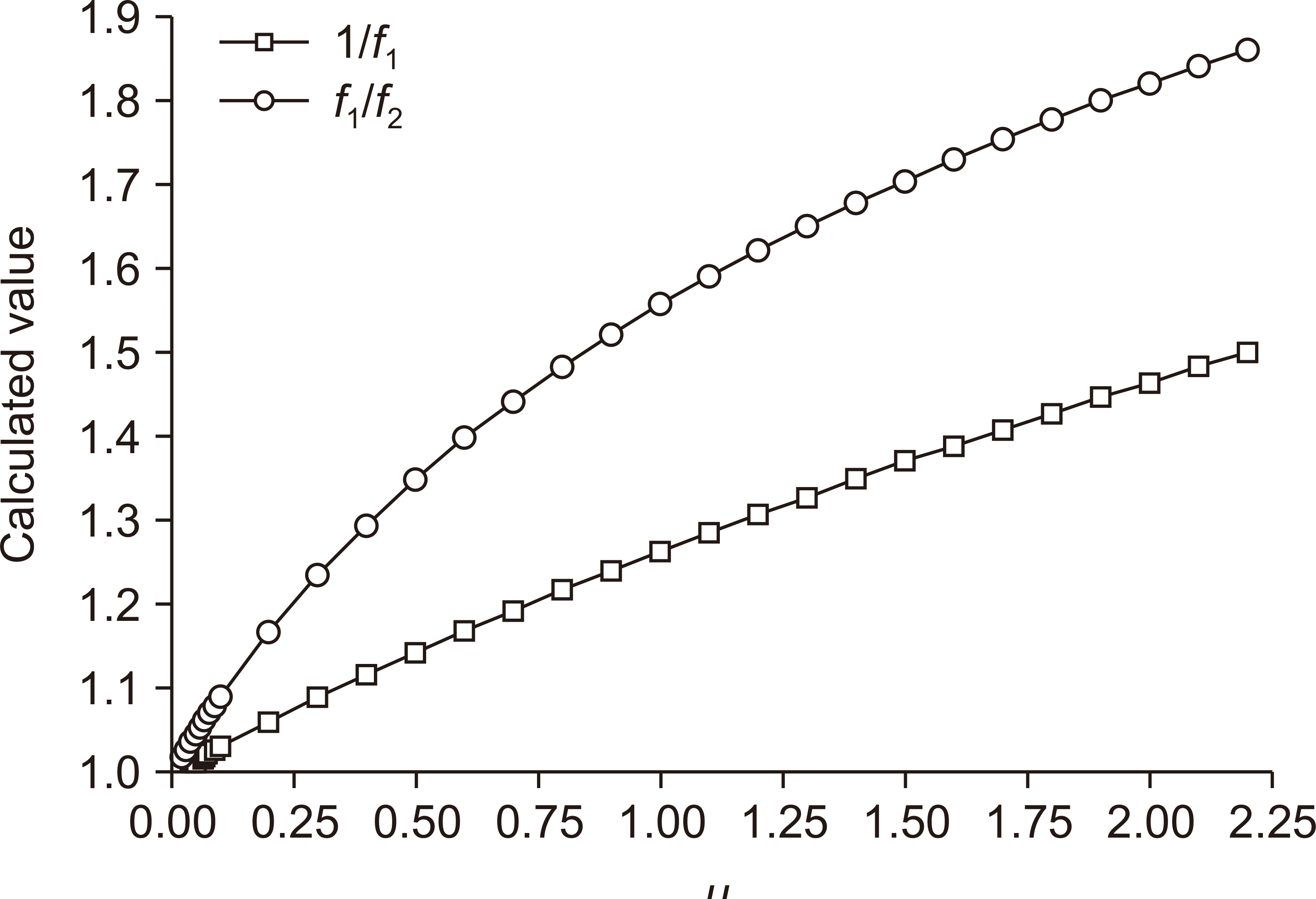
Equation (3) cannot be solved directly due to the difficulty in determining the parameter u. However, if f₁ and f₂ are the ion-collection efficiencies for the charges M₁ and M₂ measured at the two polarizing voltages V₁ and V₂, respectively, then the ratio f₁/f₂=M₁/M₂ can be expressed a function of u₁ by using u₁/u₂=V₂/V₁:

(4)

$\frac{f_{1} (u_{1})}{f_{2} (u_{1})} = \frac{λ_{1} + \frac{1}{u_{1}} ln [1 + \frac{e^{λ_{1} (1 - λ_{1}) u_{1}} - 1}{λ_{1}}]}{λ_{2} + \frac{1}{(\frac{V_{1}}{V_{2}}) u_{1}} ln [1 + \frac{e^{λ_{2} (1 - λ_{2}) (\frac{V_{1}}{V_{2}}) u_{1}} - 1}{λ_{2}}]} = \frac{M_{1}}{M_{2}} .$

Then, one can determine u₁ iteratively using a computer program and the measured value of M₁/M₂. The correction factor k_s=1/f1 can be determined by substituting the resulting value of u₁ into the expression for f₁. This is the method proposed by Boag et al. (1996) [6] and implemented by Laitano et al. (2006) [7]. However, although this method can be used to determine ks, applying in practice is inconvenient.

Conversely, because the single variable u₁ determines both M₁/M₂ and f₁ simultaneously, the correction factor k_s=1/f₁ can be determined as a function of M₁/M₂ without iteration by utilizing pre-calculated values of M₁/M₂ and f₁ as functions of u₁. Thus, the quantity f₁ can be obtained as a function of M₁/M₂ for practical use by fitting. Our study used this new method with the new equations based on the Boag model, to measure high-DPP electron beams produced by an electron LINAC.

2. Verification of the calculations

Laitano et al. [7] investigated Boag’s three improved models and published the ion-recombination factors determined for six types of commercial plane-parallel ionization chambers for various polarization voltages. For comparison with our method, we selected 22 of the data points obtained by Laitano et al. [7] for comparison. The selected data cover the range 0.1–70 mGy/pulse and include values of M₁/M₂ up to about 2, as measured at 10 voltage ratios with an Exradin A12 ionization chamber. We solved equation (4) for the given M₁/M₂ values and two polarization voltages, and we fitted the k_s values as a function of M₁/M₂ with second-order polynomial functions. We employed the same physical parameters used by Laitano et al. [7] in our calculations of equation (4).

3. Electron-beam measurements

To determine the reference dose in water at source-to-surface distance (SSD)=100 cm, we performed dosimetry for electron beams from a 6 MeV electron LINAC using an Advanced Markus^® ionization chamber, as shown in Fig 1. The electron LINAC used in this study is the prototype developed by the Dongnam Institute of Radiological and Medical Science in collaboration with the Pohang Accelerator Laboratory [14]. Because the electron energy depends on the heating current of the electron gun, this experiment was performed at about 6 MeV by adjusting the heating current [15].

Fig. 1

Experimental setup (a) for reference dosimetry using an Advanced Markus^® chamber and (b) for percentage depth dose measurements using a radiochromic film in water. LINAC, linear accelerator.

An electron-irradiation device was used for the electron-beam irradiations, as shown in Fig. 1. It consists of specially designed scattering foils and collimators to generate an optimal electron beam for FLASH preclinical studies. We do not discuss its detailed geometry in the present work because the irradiation device is still under study.

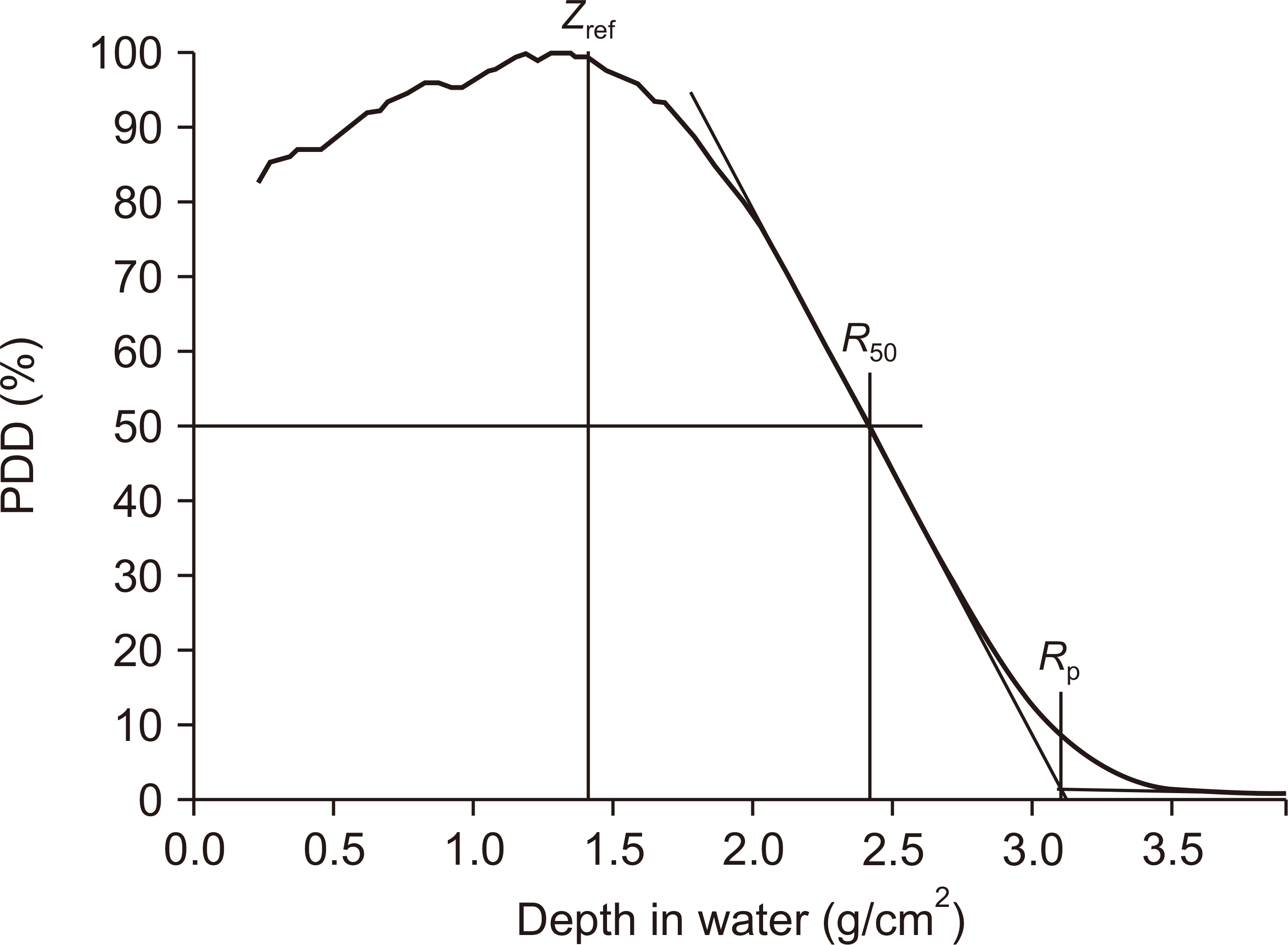
The ionization chamber was calibrated in terms of water equivalents using a Co-60 reference beam. We applied the TRS-398 protocol to determine the dose in water [11]. The reference point of the ionization chamber was positioned at z_ref=0.6R₅₀−0.1 cm, where R₅₀ is the half-value depth in water [11]. In this work, we determined R₅₀ by measuring the percentage depth dose (PDD) curve using a radiochromic film. The ionization measurements were performed at polarization voltages of 400 V and 200 V for 100 electron-beam pulses at the repetition rate of 50 Hz using pulse-mode control of the pulse-modulator system [16]. We applied the values of k_s calculated with the new method to correct the measured charge, and we also applied environmental and polarity corrections according to the TRS-398 protocol [11].

Go to :

Results

1. Calculation and verification

Fig. 2 shows f₁/f₂ and 1/f₁ calculated as a function of u₁ for V₁/V₂=400/200 using equations (3) and (4) for the Advanced Markus^® chamber, a plane-parallel ionization chamber with an electrode spacing of 1 mm. The value of k_s can be determined as a function of M₁/M₂, because k_s=1/f₁ and M₁/M₂=f₁/f₂.

Fig. 2

Ratio of the ion-collection efficiency (f₁/f₂) and the correction factor (1/f₁) calculated as a function of u₁ using Boag’s model.

In this manner, we calculated k_s for the 22 selected data points, and the calculated results are shown in Fig. 3 together with the results of Laitano et al. [7]. Here, Fig. 3a and Fig. 3b, respectively, are for cases with small and with large slopes of k_s as a function of M₁/M₂ [7]. Comparing the calculated and published values of ks shows good agreement, i.e., to within 0.1%.

Fig. 3

Comparison of the ion-recombination correction factors recalculated in this work with data published by Laitano et al. [7] for 5 polarizing voltage ratios. See text for the explanation of the difference between graphs (a) and (b).

The calculated values of k_s for the Advanced Markus chamber we used to measure the dosimetry of high-DPP electron beams is shown in Fig. 4. This figure shows the two k_s curves at two voltage ratios obtained with the new method (based on Boag’s model) and the two corresponding k_s curves calculated using current methods (those of the IAEA and the AAPM). The k_s curves obtained using the new method can be fitted with the following function for practical use:

Fig. 4

The ion-recombination correction factors at V₁/V₂=400/200 and V₁/V₂=300/100 calculated in this work using Boag’s model. The correction factors calculated by the conventional methods are included for comparison.

(5)

$k_{s} {=b}_{0} {+b}_{1} (\frac{M_{1}}{M_{2}}) {+b}_{2} {(\frac{M_{1}}{M_{2}})}^{2} .$

Here, b₀=1.3890, b₁=−0.9705, and b₂=0.5819 for polarization voltage ratio V₁/V₂=400/200 and b₀=1.0413, b₁=−0.1549, and b₂=0.1157 for V₁/V₂=300/100. In Fig. 4, the values of k_s obtained with the currently used IAEA TRS-398 and AAPM TG-51 protocols are similar, but they are higher than those obtained with Boag’s model. Compared to the k_s value for M₁/M₂=1.10 at V₁/V₂=400/200, the results from the IAEA TRS-398 and AAPM TG-51 protocols differed by about 8.9% and 8.2%, respectively, although no significant difference was found in the range M₁/M₂<1.01.

2. Electron-beam measurements

The PDD curve measured with radiochromic film in water to determine the beam-quality index R₅₀ (=2.4 g/cm²) is shown in Fig. 5. The mean electron energy at the phantom surface,

$\bar{E}$ =2.33 R₅₀=5.6 MeV, and the most probable energy, E_p=0.22+1.98 R_p+0.0025 R_p² ≈ 6.4 MeV, can be determined from the PDD plot in Fig. 5, where R_p (=3.1 g/cm²) is defined as the practical range of the electron beam in water [17]. These parameters are similar to those of a clinical electron beam with a nominal energy of 6 MeV [17].

Fig. 5

Measured percentage depth dose (PDD) curve used to determine the beam-quality index R₅₀, including the reference depth z_ref and the practical range R_p.

We took into account the 0.2-cm-thick window made of polymethyl methacrylate, with a density of 1.19 g/cm³, in determining the measurement depth. The reference depth, z_ref=1.38 g/cm², and the beam-quality factor as functions of R₅₀ were taken from the tabulated value for the Markus chamber in the TRS-398 protocol. The determined dose in water at the reference depth is listed in Table 1. Because the measured dose D (z_ref) in the table is for 100 electron-beam pulses at a 50 Hz repetition rate, the average dose rate is 5.75 Gy/s, and DPP (z_ref)=115 mGy/pulse. The combined standard uncertainty in this measurement is estimated to be 2.4% (coverage factor k=1), which includes contributions from the measured value (0.1%), the ion-recombination correction factor (2.0%), a polarity correction factor (0.4%), an air-density correction factor (0.2%), an ionization-chamber calibration factor (0.6%), a quality factor (1.0%), and others (0.5%). Here, we assumed the uncertainty in the ion-recombination correction factor to be the value given by Boag [6].

Table 1

Summary of the LINAC operating parameters and electron-beam dosimetry results

Quantity and parameters	Value
LINAC operation
RF average power	2.5 MW
Pulse repetition rate	50 Hz
Pulse width	2.5 μs
Electron-gun heater current	2.1 A
Number of pulses per irradiation	100
Dosimetry
Ionization chamber	Advanced Markus
Electrometer	PTW UNIDOSwebline
Phantom material	Water
Beam quality index, R50	2.4 g/cm2
Measurement depth, zref	1.38 g/cm2
M1 (+400 V)	(9.049±0.187) nC
M2 (+200 V)	(8.262±0.217) nC
M– (–400 V)	(–9.071±0.078) nC
M1/M2	1.095
ks (M1/M2)	1.024
kpol	1.001
kTP	1.029
M corrected	9.544 nC
	1.308 Gy/nC
	0.921
Absorbed dose, D (zref)	11.50 Gy
Dose-per-pulse, DPP (zref)	115 mGy/pulse
Combined uncertainty (k = 1)	2.4%

LINAC, linear accelerator.

Go to :

Discussion

In applying Boag’s model to calculate the ion-recombination correction factor, we verified that the results calculated by our method are the same as those calculated by the iterative numerical method. Our new method can be applied in practical applications without iterative calculations, and it can be presented in the form of the equation currently used in the TRS-398 protocol.

It is important to note that only the voltage ratio V ₁/V ₂ is used in the TRS-398 and TG-51 protocols. However, to determine the correction factor, two voltages must be applied separately to use Boag’s model. This means, for example, that for the two voltage ratios V ₁/V ₂=400/200 and V ₁/V ₂=300/150, the same correction factor is calculated from the TRS-398 and TG-51 protocols, but the results are different in Boag’s model for M ₁/M ₂>1.3. In addition, the current method is independent of the type of ionization chamber, but Boag’s model requires the electrode spacing of the ionization chamber in order to calculate the electric field in the cavity [6]. In high-DPP (>200 mGy/pulse) or FLASH beams, higher values of M ₁/M ₂ require additional verification. However, performing such additional verifications is currently difficult due to the lack of reported data.

Although several forms of the relationship between high DPP and the ion-collection efficiency of the ionization chambers used for absolute dosimetry were reported [5,8], applying these results directly to obtain dose determinations using an ionization chamber is difficult without performing absolute dosimetry. Film dosimetry may be exploited instead of absolute dosimetry for studying the ion-recombination correction factor for high-DPP beams, although the accuracy is limited. Further, since Boag’s theory has not been validated for high-DPP (>200 mGy/pulse) beams, in this study we performed the measurements only for a dose rate obtained at SSD=100 cm.

Go to :

Conclusions

We carried out the present study in order to devise a practical method of applying Boag’s improved model for the dosimetry of high-dose-rate electron beams using commercial ionization chambers. This correction method can be applied to DPP ranges up to about 120 mGy/pulse. This upper limit is a suggested value based on the verification of Laitano et al. [7]. It can also be applied to electron beams of higher DPP, subject to independent verifications.

The estimated dose rate of electron beams used in this study is 11.50 Gy/s, assuming a LINAC pulse repetition rate of 100 Hz. This value is lower than that required in FLASH preclinical studies [2,3]. However, the dose rate can be increased significantly by reducing the SSD, as shown in a previous study using our LINAC system [16]. We plan to continue additional studies on the development of correction methods for FLASH beams, eventually applying the results to the construction and commissioning of a FLASH electron-beam irradiation system.

Go to :