1. Ma CMC, Chetty IJ, Deng J, Faddegon B, Jiang SB, Li J, et al. 2020; Beam modeling and beam model commissioning for Monte Carlo dose calculation-based radiation therapy treatment planning: Report of AAPM Task Group 157. Med Phys. 47:e1–e18. DOI:
10.1002/mp.13898. PMID:
31679157.

2. Wanklyn MD, Kidane G, Crees L. 2016; Verification measurements of an eMC algorithm using a 2D ion chamber array. J Appl Clin Med Phys. 17:320–328. DOI:
10.1120/jacmp.v17i5.6150. PMID:
27685111. PMCID:
PMC5874119.

3. Chetty IJ, Curran B, Cygler JE, DeMarco JJ, Ezzell G, Faddegon BA, et al. 2007; Report of the AAPM Task Group No. 105: issues associated with clinical implementation of Monte Carlo-based photon and electron external beam treatment planning. Med Phys. 34:4818–4853. DOI:
10.1118/1.2795842. PMID:
18196810.

4. Pemler P, Besserer J, Schneider U, Neuenschwander H. 2006; Evaluation of a commercial electron treatment planning system based on Monte Carlo techniques (eMC). Z Med Phys. 16:313–329. DOI:
10.1078/0939-3889-00330. PMID:
17216757.

5. Fix MK, Frei D, Volken W, Neuenschwander H, Born EJ, Manser P. 2010; Monte Carlo dose calculation improvements for low energy electron beams using eMC. Phys Med Biol. 55:4577–4588. DOI:
10.1088/0031-9155/55/16/S11. PMID:
20668339.

6. Cygler JE, Daskalov GM, Chan GH, Ding GX. 2004; Evaluation of the first commercial Monte Carlo dose calculation engine for electron beam treatment planning. Med Phys. 31:142–153. DOI:
10.1118/1.1633105. PMID:
14761030.

7. Xu Z, Walsh SE, Telivala TP, Meek AG, Yang G. 2009; Evaluation of the eclipse electron Monte Carlo dose calculation for small fields. J Appl Clin Med Phys. 10:75–85. DOI:
10.1120/jacmp.v10i3.2834. PMID:
19692969. PMCID:
PMC5720559.

8. Ding GX, Duggan DM, Coffey CW, Shokrani P, Cygler JE. 2006; First macro Monte Carlo based commercial dose calculation module for electron beam treatment planning--new issues for clinical consideration. Phys Med Biol. 51:2781–2799. DOI:
10.1088/0031-9155/51/11/007. PMID:
16723766.

9. Neuenschwander H, Born EJ. 1992; A macro Monte Carlo method for electron beam dose calculations. Phys Med Biol. 37:107–125.

10. Zhang A, Wen N, Nurushev T, Burmeister J, Chetty IJ. 2013; Comprehensive evaluation and clinical implementation of commercially available Monte Carlo dose calculation algorithm. J Appl Clin Med Phys. 14:127–145. DOI:
10.1120/jacmp.v14i2.4062. PMID:
23470937. PMCID:
PMC5714370.

11. Chamberland E, Beaulieu L, Lachance B. 2015; Evaluation of an electron Monte Carlo dose calculation algorithm for treatment planning. J Appl Clin Med Phys. 16:60–79. DOI:
10.1120/jacmp.v16i3.4636. PMID:
26103470. PMCID:
PMC5690146.

12. Łukomska S, Kukołowicz P, Zawadzka A, Gruda M, Giżyńska M, Jankowska A, et al. 2016; Evaluation of the usefulness of the electron Monte Carlo algorithm for planning radiotherapy with the use of electron beams. Pol J Med Phys Eng. 22:49–54.

13. Jong WL, Ung NM, Tiong AHL, Rosenfeld AB, Wong JHD. 2018; Characterisation of a MOSFET-based detector for dose measurement under megavoltage electron beam radiotherapy. Radiat Phys Chem. 144:76–84.

14. Fix MK, Cygler J, Frei D, Volken W, Neuenschwander H, Born EJ, et al. 2013; Generalized eMC implementation for Monte Carlo dose calculation of electron beams from different machine types. Phys Med Biol. 58:2841–2859. DOI:
10.1088/0031-9155/58/9/2841. PMID:
23563175.

15. Ojala J, Kapanen M, Hyödynmaa S. 2016; Full Monte Carlo and measurement-based overall performance assessment of improved clinical implementation of eMC algorithm with emphasis on lower energy range. Phys Med. 32:801–811. DOI:
10.1016/j.ejmp.2016.05.005. PMID:
27189311.

16. Varian Medical Systems. 2015. Eclipse photon and electron algorithms reference guide. Varian Medical Systems;Palo Alto:
17. Shimozato T, Kojima T, Sakamoto M, Hata Y, Sasaki K, Araki N. 2012; Evaluating the output stability of LINAC with a reference detector using 3D water phantom. Igaku Butsuri. 32:176–181. PMID:
24568022.
18. Khan FM, Gibbons JP. 2014. Khan’s the physics of radiation therapy. Lippincott Williams & Wilkins;Philadelphia:
19. Brualla L, Palanco-Zamora R, Wittig A, Sempau J, Sauerwein W. 2009; Comparison between PENELOPE and electron Monte Carlo simulations of electron fields used in the treatment of conjunctival lymphoma. Phys Med Biol. 54:5469–5481. DOI:
10.1088/0031-9155/54/18/008. PMID:
19706962.

20. Edimo P, Kwato Njock MG, Vynckier S. 2013; Validation of XiO Electron Monte Carlo-based calculations by measurements in a homogeneous phantom and by EGSnrc calculations in a heterogeneous phantom. Phys Med. 29:631–638. DOI:
10.1016/j.ejmp.2012.08.004. PMID:
23010450.

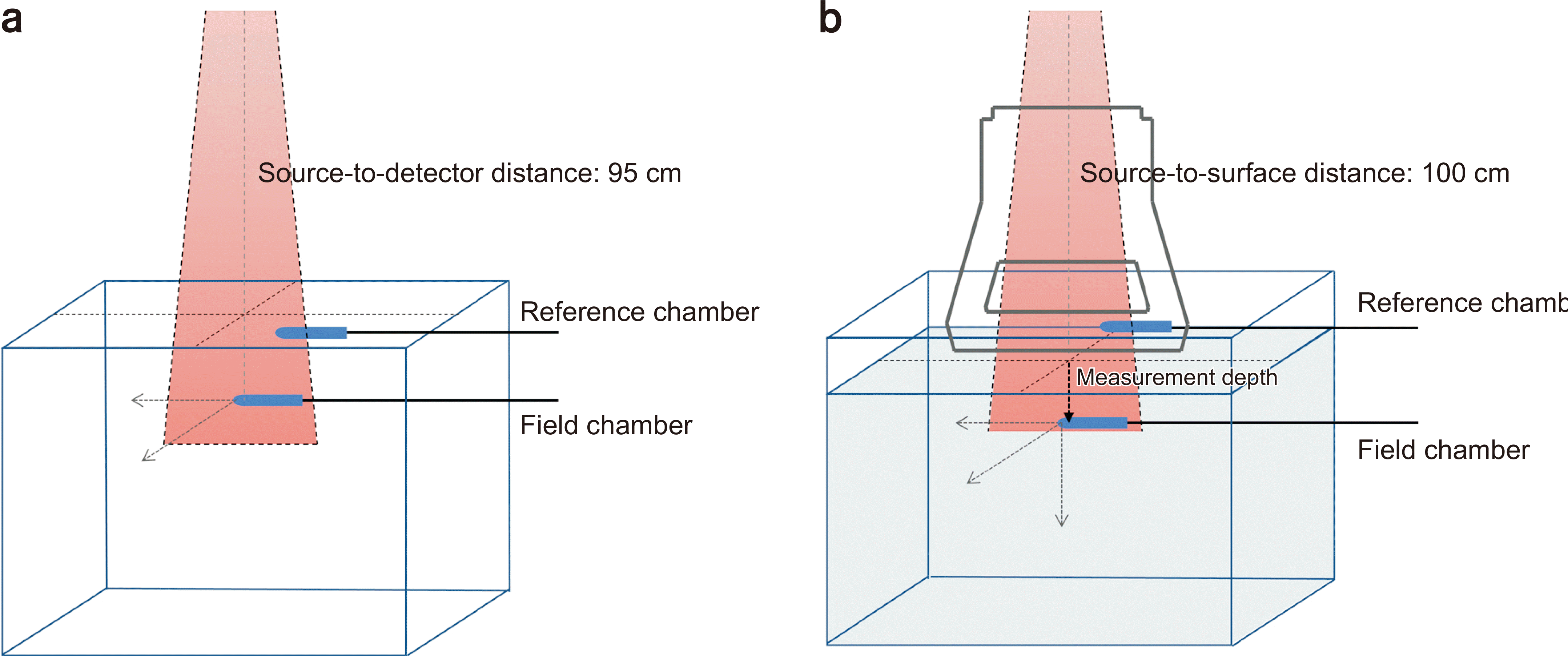




 PDF
PDF Citation
Citation Print
Print



 XML Download
XML Download