PDF
Citation
Print
INTRODUCTION
Orthodontists treat skeletal and dental malocclusions. They initially assess the patient’s skeletal pattern, and then decide whether the orthodontic treatment should be combined with an orthognathic surgery. Orthodontic treatment without an orthognathic surgery is a process of inducing an artificial form of dentoalveolar compensation, which is the primary mechanism in individuals with normal occlusion. Although these individuals show certain amounts of skeletal discrepancy, a well-coordinated dentoalveolar compensation can ensure normality of the occlusion. Therefore, a careful assessment of the characteristics of normal samples is necessary for establishing the treatment goal.
Many studies on dentoalveolar compensatory mechanisms have been reported,1-3 and significant anatomical variations in samples of normal occlusion have been widely discussed.4-7 The study by Casko and Shepherd5 reported that naturally occurring A point-nasion-B point angles ranged from –3.0° to 8.0°, and these findings were identical to the results reported by Kim et al.,7 who classified normal subjects into nine skeletal patterns and suggested characteristic features of dentoalveolar compensation for each of the nine groups. However, most of those studies mainly dealt with anteroposterior relationship.
Openbite malocclusion, one of the most challenging forms of malocclusion, can be orthodontically treated by intruding molars with the help of a skeletal anchorage system. However, the high potential of relapse after this treatment still challenges the orthodontists.8-10 To ensure the stability of the treatment, tooth movement within the range of biological adaptation relative to the skeletal pattern is essential, especially for non-surgical orthodontic treatment of openbite cases. Clues regarding the biologically acceptable range of tooth movements can be obtained from normal occlusion samples with diverse skeletal patterns. An adequate understanding of the individual norms for compensation may facilitate the development of individualized treatment plans. Since such intrusive tooth movement is usually planned in millimeters, linear measurement is more practical than angular measurement. However, only a few studies have analyzed the molar position using linear measurements.
Considering the envelope of discrepancy by Proffit and Sarver11 as the possible range of tooth movement, intrusive orthodontic tooth movement is known to be difficult. However, since the skeletal anchorage system is widely used in orthodontics, remarkable success of the intrusion in orthodontic tooth movement has been reported. The possible range of vertical tooth movement in the Proffit’s envelope has been extended, and the related vertical analysis of dentition in cephalometry has drawn much attention not only for malocclusion samples but also for normal samples. However, in cephalometry, most of the vertical measurements are for skeletal values and dental values are usually anteroposterior measurements. With the enlargement of the possible range of vertical tooth movement, vertical measurements of dentition have become essential, and in this regard, linear values are more intuitive and practical for clinical usage than angular values. Unlike cephalometric analysis using angular values, the analysis using linear values requires a calibration process for each individual because the head size varies widely, like the height of individuals. Some cephalometric studies used the anterior cranial base (ACB) length as a reference structure to evaluate the mandibular body length. However, this approach represents calibration of linear measurements in the anteroposterior dimension, and few studies have attempted to calibrate linear measurements in the vertical dimension, especially using the posterior cranial base (PCB) length as a reference structure.
Thus, the aim of this study was to evaluate the correlations among vertical measurements in the lateral cephalograms of normal samples and identify vertical skeletal variables that show correlation with the vertical position of the maxillary first molar (U6) by using vertical linear measurements calibrated on the vertical axis of coordinates.
Go to : 
MATERIALS AND METHODS
Samples
The samples were obtained from 103 non-growing Koreans (52 males, 51 females; average age, 23 years 9 months) among the normal occlusion samples in the Department of Orthodontics, Seoul National University Dental Hospital. The selection criteria were skeletal Class I relationship, Class I molar and canine relationships with normal overbite and overjet, minimal crowding (arch length discrepancy less than 1 mm), fully erupted permanent dentition except third molars, absence of supernumerary or malformed teeth, no temporomandibular joint disorder, and no history of previous orthodontic treatment.
Cephalometric analysis
Lateral cephalograms were taken and traced. The tracings were then digitized with a digitizer (INTUOS 2 graphic tablet; Wacom Technology Co., Vancouver, Canada) and analyzed using V-Ceph® (Osstem, Seoul, Korea) by a single investigator. Reference lines and cephalometric landmarks are listed in Figure 1.
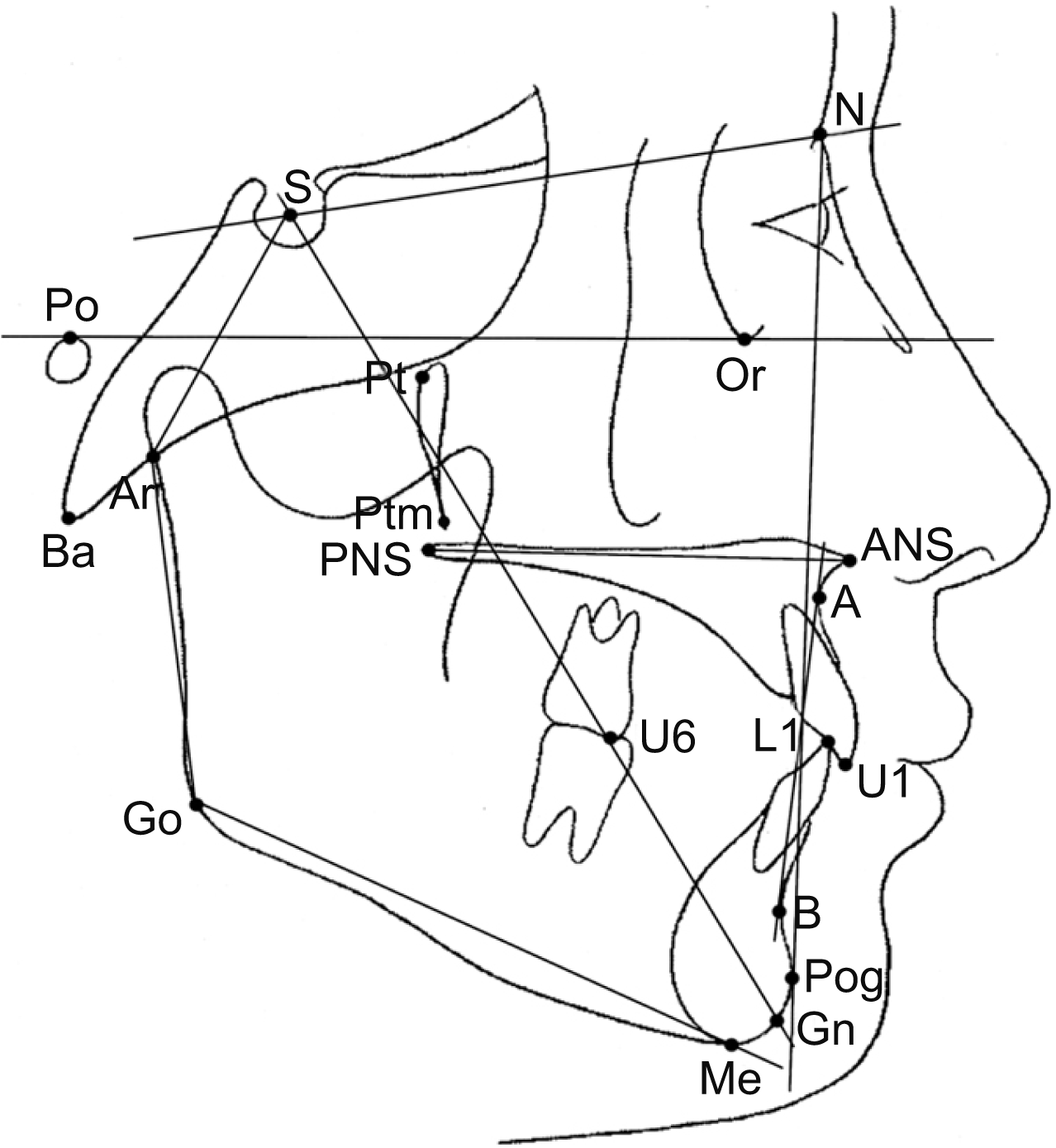 | Figure 1Cephalometric landmarks. S, sella; N, nasion; Or, orbitale; Po, porion; Ar, articulare; Ba, basion; Pt, pterygoid; Ptm, pterygomaxillary fissure; Go, gonion; Pog, pogonion; Gn, gnathion; Me, menton; ANS, anterior nasal spine; PNS, posterior nasal spine; A, A point; B, B point; U1, incisal tip of upper incisors; U6, mesiobuccal cusp of the upper first molars; L1, incisal tip of the lower incisors. Reference planes. SN, Sella-nasion; FH, porion-orbitale; ANS-PNS, palatal plane; U1-U6, occlusal plane; Go-Me, mandibular plane; nasion-pogonion, facial plane; sella-gnathion, Y axis.
|
To determine the relationship between the position of U6 and the vertical skeletal measurements, the sella-nasion (SN) plane was chosen as the horizontal reference plane because of its distinctiveness for measurement and anatomic stability as an ACB. The vertical skeletal measurements included 10 conventionally used measurements (ConV: nine angular values and one ratio value) (Table 1) and six uniquely derived linear values (NwLin) (Figure 2). ConV were the widely used measurements for vertical skeletal patterns in cephalometric analyses and NwLin were the newly developed measurements that aimed to analyze the relative vertical distance of the maxilla to the upper-level skeletal structures of the head.
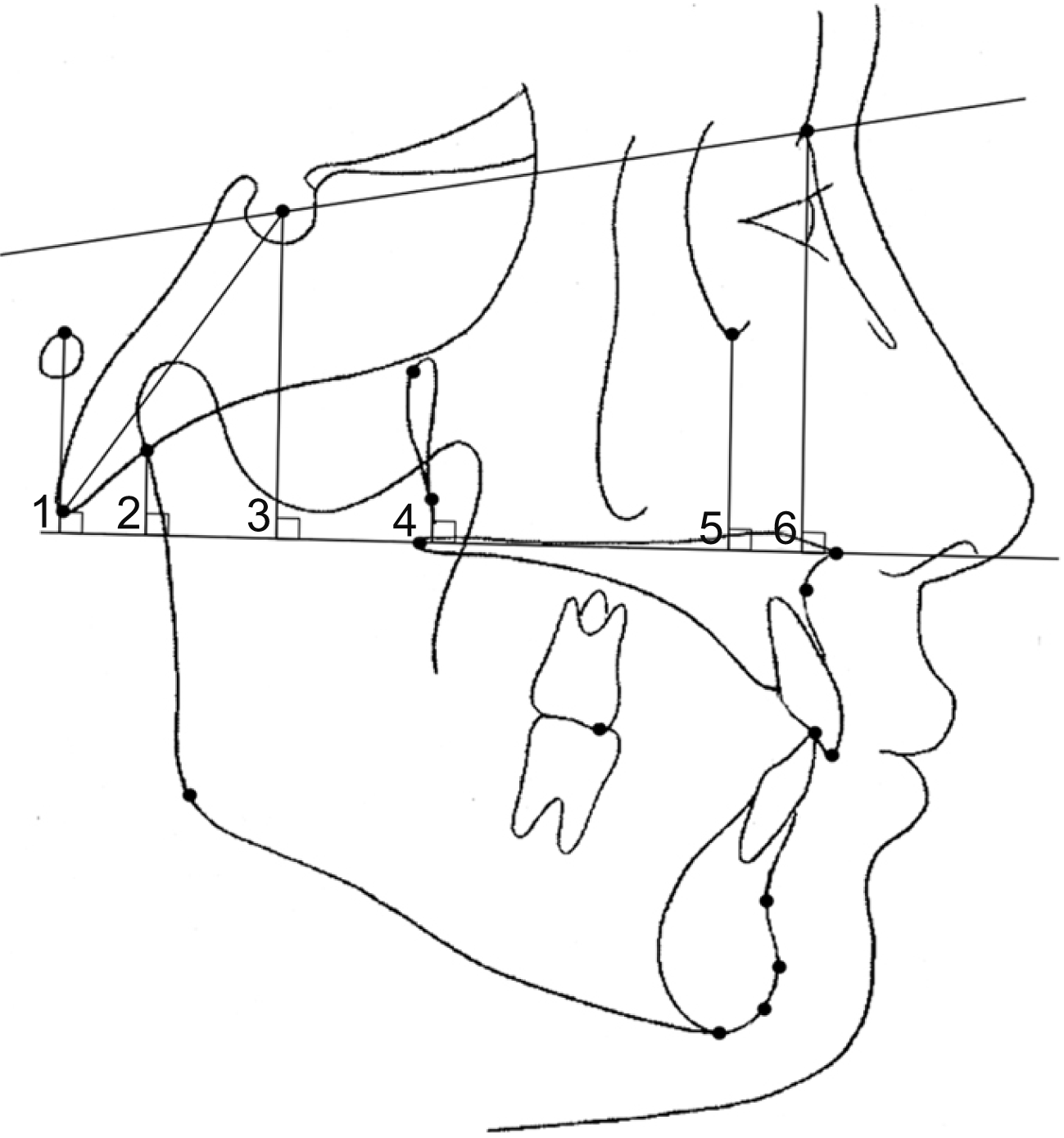 | Figure 2Vertical linear measurements used exclusively in this study: 1, Po to palatal plane; 2, Ar to palatal plane; 3, S to palatal plane (posterior component of the maxilla); 4, Ptm to palatal plane; 5, Or to palatal plane; 6, N to palatal plane (anterior component of the maxilla).
See Figure 1 for definition of each landmark.
|
Table 1
Conventionally used vertical skeletal measurements in this study
See Figure 1 for definition of each landmark.
Subsequently, any variables correlating with the vertical position of U6 (U6-SN) were evaluated, and the remaining independent variables underwent further analysis. To remove inter-correlations among these independent variables as well as to identify the more important variables that could be used for prediction of the vertical position of U6, a regression model was obtained with the sex and the cephalometric variables. To determine the best approach for calibration in the vertical dimension, each set of statistical analyses was performed three times: with the raw values, values calibrated to ACB length, and values calibrated to PCB length. The calibration was for prevention of bias due to the differences in individual head sizes.
The institutional review board of Seoul National University School of Dentistry for the protection of human subjects reviewed and approved the research protocol (No. S-D20150012).
Statistical analysis
To analyze the test-retest reliability of cephalometric analysis, 40 samples were randomly selected and measured 4 weeks after the initial measurement, and intra-class correlation coefficients were computed. To identify variables that were correlated with U6-SN, Pearson correlation analysis was performed. Regression models were obtained through multiple linear regression analyses. In all statistical analyses, p-values < 0.05 were considered statistically significant. Data were statistically processed with an open-source statistical software package (R ver. 3.4.2.; Free Software Foundation, Boston, MA, USA).
Go to :
RESULTS
The intra-class correlation coefficients were between 0.923 and 0.988 (p < 0.01) for all measurements. This result substantiated the reliability of repeated measurements by the investigator.
The Pearson correlation analyses showed the variables that significantly correlated with the vertical position of U6 among the 16 skeletal measurements. In this study, correlation coefficients greater than +0.20 and less than –0.20 showed statistical significance (r > +0.26, r < –0.26, p < 0.01; r > +0.20, r < –0.20, p < 0.05, two-tailed). In the analysis with the raw values of linear measurements (RawS), four of the 10 ConV and all six NwLin were statistically correlated with U6-SN. In the analysis performed using measurements calibrated to ACB length (CalACB), five of the 10 ConV and all six NwLin were statistically correlated with U6-SN, which was also calibrated to ACB length. In the analysis performed using measurements calibrated to PCB length (CalPCB), eight of the 10 ConV and all six NwLin showed statistically significant correlations with U6-SN, which was also calibrated to PCB length. Each correlated variable showed an increasing level of significance in the order of analyses with raw values, calibration to ACB length, and calibration to PCB length (Table 2).
Table 2
Pearson correlation analyses related to the vertical position of the maxillary first molar
| Measurement | Raw value |
Values calibrated to ACB length |
Values calibrated to PCB length |
|||||
|---|---|---|---|---|---|---|---|---|
|
|
|
|
||||||
| Pearson correlation coefficient (r) | p-value | Pearson correlation coefficient (r) | p-value | Pearson correlation coefficient (r) | p-value | |||
| Angular | ||||||||
| Articular angle | –0.095 | 0.338 | 0.161 | 0.105 | 0.146 | 0.142 | ||
| Saddle angle | 0.043 | 0.667 | 0.000 | 0.996 | 0.103 | 0.300 | ||
| Upper gonial angle | –0.233 | 0.018* | –0.569 | < 0.001*** | –0.341 | < 0.001*** | ||
| Lower gonial angle | 0.075 | 0.453 | 0.226 | 0.022* | 0.334 | 0.001** | ||
| Björk sum | –0.199 | 0.043* | –0.015 | 0.883 | 0.347 | < 0.001*** | ||
| Facial axis | –0.137 | 0.168 | –0.339 | < 0.001*** | –0.330 | 0.001** | ||
| SN to Go-Me | –0.200 | 0.043* | –0.015 | 0.882 | 0.347 | < 0.001*** | ||
| SN to Y-axis | 0.034 | 0.733 | 0.207 | 0.036* | 0.250 | 0.011* | ||
| ODI | 0.144 | 0.147 | –0.098 | 0.327 | –0.284 | 0.004** | ||
| Ratio | ||||||||
| Facial height ratio | 0.373 | < 0.001*** | 0.213 | 0.031* | –0.294 | 0.003** | ||
| New linear | ||||||||
| S to palatal plane | 0.740 | < 0.001*** | 0.704 | < 0.001*** | 0.822 | < 0.001*** | ||
| N to palatal plane | 0.665 | < 0.001*** | 0.696 | < 0.001*** | 0.884 | < 0.001*** | ||
| Or to palatal plane | 0.560 | < 0.001*** | 0.552 | < 0.001*** | 0.731 | < 0.001*** | ||
| Ptm to palatal plane | 0.361 | < 0.001*** | 0.395 | < 0.001*** | 0.659 | < 0.001*** | ||
| Po to palatal plane | 0.358 | < 0.001*** | 0.348 | < 0.001*** | 0.616 | < 0.001*** | ||
| Ar to palatal plane | 0.365 | < 0.001*** | 0.238 | 0.015* | 0.679 | < 0.001*** | ||
See Figure 1 for definition of each landmark.
The statistically significant variables from each set of the three correlation analyses and sex were used for regression analysis. Each of the three regression models was constructed with the final two variables (p < 0.01), which were the distances from the sella to the palatal plane (PP) (posterior component of the maxilla) and the nasion to the PP (anterior component of the maxilla) (Figure 3). The adjusted R2 values of the models with RawS, CalACB, and CalPCB were 0.709, 0.717, and 0.880, respectively. Sex did not have any effect in all three regression models (p > 0.05) (Table 3). Both variables showed positive coefficients for all three models (Figure 4; only the best fitting model of CalPCB is shown).
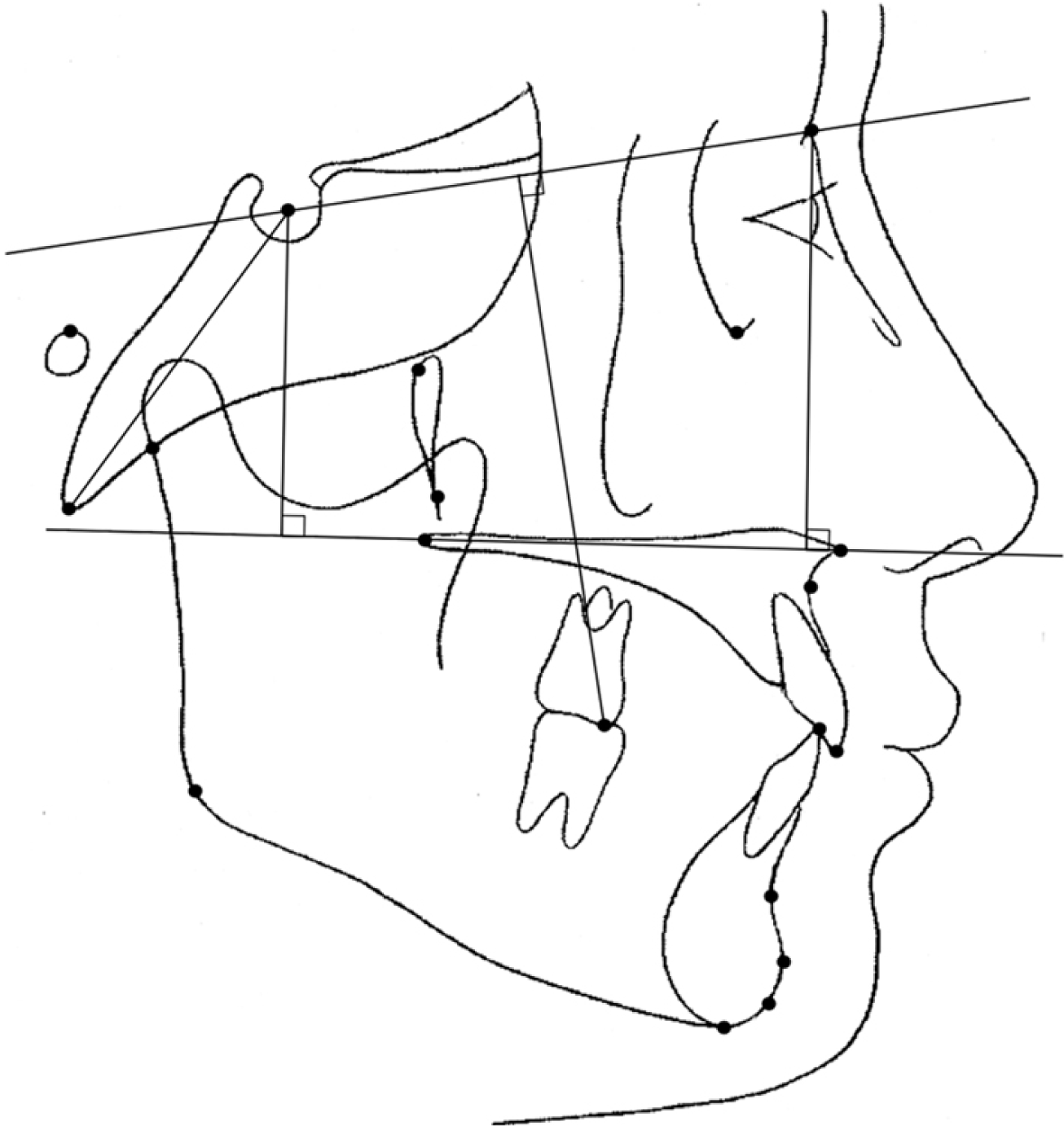 | Figure 3Final variables included in the regression models. Posterior component of the maxilla (sella to palatal plane); anterior component of the maxilla (nasion to palatal plane).
|
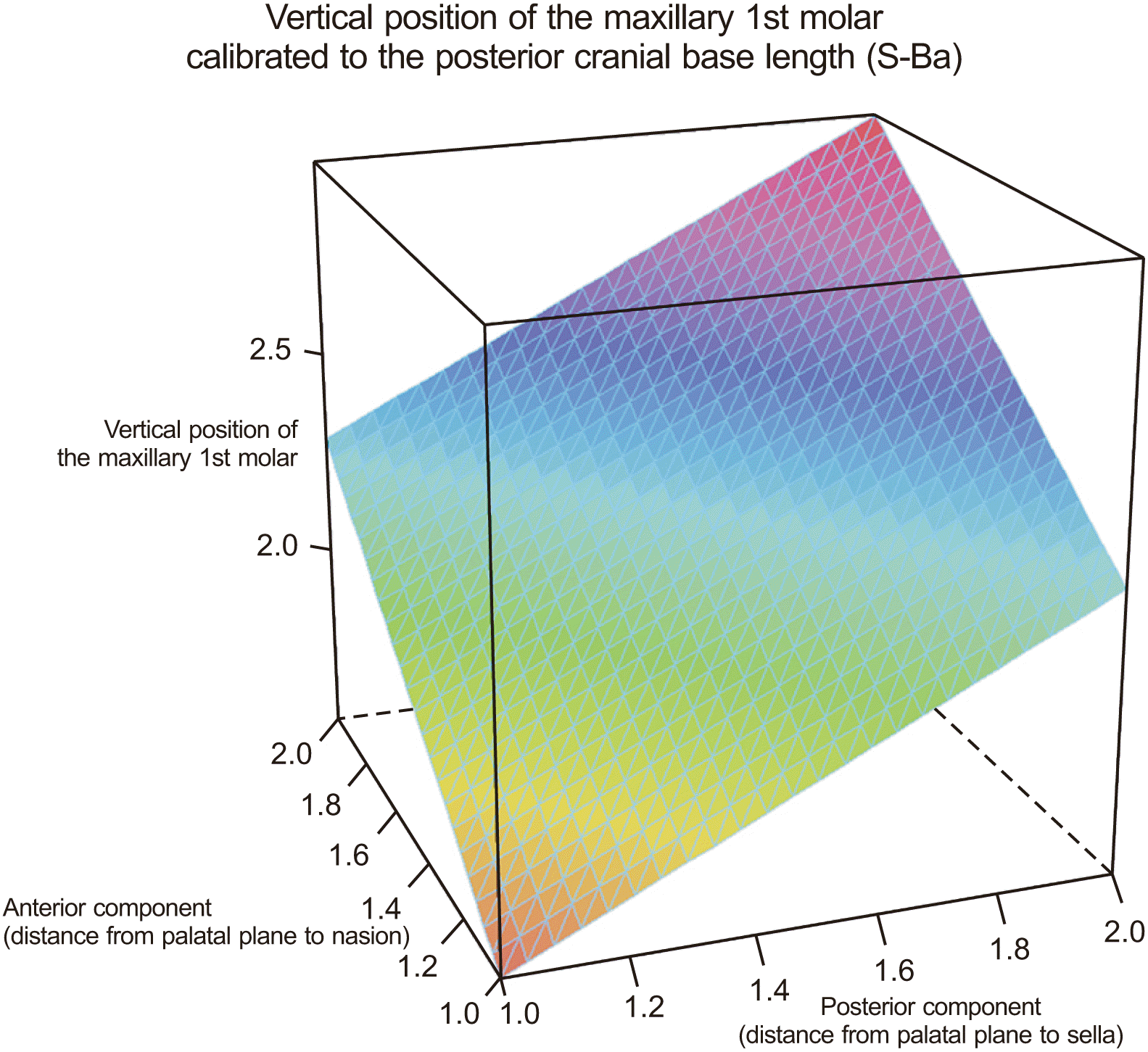 | Figure 4Three-dimensional wireframe plots of the final linear regression model with the posterior component of the maxilla (sella to palatal plane) and the anterior component of the maxilla (nasion to palatal plane) to predict the vertical position of the maxillary first molar (U6-SN), calibrated to the posterior cranial base length.
|
Table 3
Results of the multiple regression to identify variables that influence the vertical position of the maxillary first molar
|
Vertical position of the maxillary first molar* |
Independent variable | Significance | Adjusted R2 |
|---|---|---|---|
| Raw linear distance (mm) | 0.7092 | ||
| Sex | 0.6070 | ||
| Posterior component§ | < 0.0001 | ||
| Anterior component∥ | < 0.0001 | ||
|
When calibrated to the anterior cranial base length (mm)† |
0.7174 | ||
| Sex | 0.0634 | ||
| Posterior component | < 0.0001 | ||
| Anterior component | < 0.0001 | ||
|
When calibrated to the posterior cranial base length (mm)‡ |
0.8797 | ||
| Sex | 0.4270 | ||
| Posterior component | < 0.0001 | ||
| Anterior component | < 0.0001 |
Go to :
DISCUSSION
Many previous studies have evaluated skeletal and dental variations within the range of normal.4-7,12 Solow described that the dentoalveolar compensatory mechanism was necessary to coordinate the position of teeth relative to their basal bones.2 This mechanism is important for good occlusion as well as for stability. Because the coordination of the upper and lower jawbones is not always perfect during and after growth even in subjects with a normal occlusion, the dentoalveolar compensatory mechanism plays a major role in ensuring good occlusion. Kim et al.7 also pointed out that the skeletal patterns of individuals with normal occlusion were highly diverse. Although the samples were primarily selected on the basis of occlusion, the anteroposterior and the vertical skeletal relationships of samples with naturally occurring normal occlusion showed some variations that could even be classified into nine groups. These results suggested that an adequate understanding of the characteristics of dentoalveolar compensation and establishment of individual treatment goals were important for successful orthodontic treatment.
However, the aforementioned studies and the other cephalometric studies mainly evaluated the anteroposterior relationships of skeletal and dental patterns. Some of these studies reported measurements of vertical relationships, but most of them assessed skeletal patterns, not dental patterns. Moreover, most of the vertical measurements were angular, which could not be considered to have solely vertical components because they were usually oblique. On the other hand, linear values with reference points are much intuitive and can be truly vertical. However, linear values should be interpreted after calibration because they are dependent on head size. In a mathematical sense, for the calibration process of vertical measurements, the axis of the standard divider should be taken into account because the cephalograms are two-dimensional. Therefore, the anteroposterior linear measurements are better calibrated to ACB length and the vertical linear measurements are better calibrated to PCB length.
The cranial base has been of interest in the orthodontic field and is usually used as a relatively stable area of the craniofacial region. Since Björk drew attention to the influence of the cranial base on jaw prognathism,13 researchers have identified a possible relationship between the cranial base configuration and the jaw relationship. However, most previous studies dealt with anteroposterior jaw relationships and/or cranial base flexure and used ACB length as a calibration index.14-22 In comparison with those studies, this study used the PCB length as a calibration index for a stable and independent vertical value to ensure that the handling dimension was consistently vertical, not anteroposterior.
Although the dentition is commonly accepted to resemble the skeletal pattern when it is appropriately compensated, only a few previous studies have pointed out the characteristics of a fully compensated dentition. However, most of these studies did not show vertical relationships and mainly focused on the anteroposterior relationships of skeletal and dental patterns. This could be attributed to a lack of measurements for vertical analysis of the dentition.
The present study identified novel linear measurements for vertical analysis of skeletal and dental structures. Using these newly derived values, statistical analyses were repeated three times with different sets of variables; first with RawS of linear measurements, then with CalACB, and finally with CalPCB. The three correlation analyses revealed several significant variables among ConV and NwLin. The number of variables with statistical significance was the least for RawS and the most for CalPCB. For the variables that were included in all three sets of results, their levels of significance showed a decreasing tendency from RawS to CalPCB through CalACB. These results could imply that calibration to PCB length for vertical linear measurements had more power for the analysis and was more applicable to the development of linear cephalometric measurements than calibration to ACB length considering the general characteristics of orthodontics for dental decompensation on the vertical axis.
After the correlation analysis, multiple linear regression analyses were performed repeatedly three times to identify more clinically important variables, each with RawS, CalACB, and CalPCB, to verify the power of the calibration. Each of the three multiple regression analyses generated a two-variable model, which consisted of measurements of the distances from sella to PP and from nasion to PP. The adjusted R2 values were 0.709, 0.717, and 0.880, respectively, all of which can be considered remarkably high for biomedical research. The results showed that NwLin could be useful for cephalometric analysis and that calibration to PCB length had greater power of explanation than raw values and calibration to ACB length.
The calibrated distance of U6 to the SN plane was highly correlated with those of the sella and nasion to the PP, i.e., the vertical position of U6 was highly correlated with the vertical position of the maxilla, which was represented by the PP. The well-compensated vertical distance of U6 from the cranium can be estimated by the vertical distance of the maxilla from the cranium. Although this result seemed quite natural and obvious, the application of numerical estimation by regression analysis may have clinical significance in treatment planning for the amount of vertical tooth movement of upper molars. Moreover, there was no statistical evidence for this result from the previous studies.
On the basis of these results, the possible limits of dentoalveolar compensation can be estimated numerically by determining the vertical position of the maxilla from the ACB. These findings can be used to predict the response to molar intrusion, allowing decision-making regarding good stability and establishment of individualized treatment goals.
Previous studies that evaluated the morphologic characteristics of vertical malocclusions reported pronounced characteristics of the mandible but yielded controversial findings in the maxilla. Some studies reported that the anterior and posterior maxillary dentoalveolar height showed no significant differences between normal and hyperdivergent subjects.23-25 Other studies suggested that the anterior and posterior maxillary dentoalveolar heights appeared to be increased in hyperdivergent skeletal subjects1,26 and openbite subjects.25,27 The results of this study demonstrated that the problem of excessive dentoalveolar heights could be related to the vertical position of the maxilla, which disagreed with the findings of previous reports because calibrated values were used in this study and direct non-calibrated measurements were used in the previous studies.
In the statistical analysis of the CalPCB set, which seemed to be more powerful than the other two sets (RawS and CalACB), the angular measurements including overbite depth indicator (ODI), SN to gonion (Go)-menton (Me), facial axis, upper gonial angle, and lower gonial angle also proved to be related to U6-SN/PCB. These angular measurements have been used as typical variables related to the skeletal vertical pattern. The negative coefficients of ODI and facial axis (r = –0.284, p < 0.05; r = –0.330, p < 0.05, respectively) and positive coefficients of SN-Go-Me and upper gonial angle (r = 0.347, p < 0.05; r = 0.334, p < 0.05, respectively) meant that the hyperdivergent skeletal pattern tended to have maxillary molars far away from the cranial base vertically.28,29 The negative coefficient of the lower gonial angle (r = –0.341, p < 0.05) was mainly due to the compensatory counter-clockwise development of the mandibular corpus in the hyperdivergent skeletal pattern.
The facial height ratio was correlated with the vertical position of U6 (r = –0.294, p < 0.05). The negative correlation coincided with the skeletal characteristics of the hyperdivergent pattern. Moreover, the six newly derived measurements of sella to PP, nasion to PP, orbitale to PP, pterygomaxillary fissure to PP, porion to PP, and articulare to PP showed statistically significant correlations with U6-SN when calibrated to PCB length. These measurements represented the vertical distances of maxilla from the anatomic structures of its upper level. Thus, the vertical position of the maxilla could be influenced by its surrounding higher-level structures, which seemed to be another manifestation of the cephalo-caudal gradient in craniofacial growth.
Although the statistical analysis in this study drew a powerful regression model to predict the vertical position of U6 with vertical skeletal variables, further studies in malocclusion subjects should be performed to improve the clinical applicability of this model.
Go to :
CONCLUSION
In cephalometric analyses with linear measurements, calibration of the vertical values to PCB length would be better than calibration to ACB length. The newly derived vertical measurements in this study with calibration to the PCB length can be used for cephalometric analysis.
The vertical position of maxillary first molars could be determined by assessing the vertical position of the maxilla from the ACB in the normal samples. This finding can be used to determine the stable vertical position of upper molars acceptable for a given skeletal frame and to establish individualized orthodontic treatment goals.
Go to :
XML Download