1. Goodfellow I, Bengio Y, Courville A. 2016. Deep learning. MIT Press;Massachusetts:
2. Bini SA. 2018; Artificial intelligence, machine learning, deep learning, and cognitive computing: what do these terms mean and how will they impact health care? J Arthroplasty. 33:2358–2361. DOI:
10.1016/j.arth.2018.02.067. PMID:
29656964.

3. Garrido Á. 2017; Brain and artificial intelligence. Brain. 8:85–90.
5. McCulloch WS, Pitts W. 1943; A logical calculus of the ideas immanent in nervous activity. Bull Math Biol. 5:15–133. DOI:
10.1007/BF02478259. PMID:
2185863.
7. Rosenblatt F. 1961. Principles of neurodynamics: perceptrons and the theory of brain mechanisms. Spartan Books;Washington D.C.: DOI:
10.21236/AD0256582.
9. Russell SJ, Norvig P. 2003. Artificial intelligence: a modern approach. 2nd ed. Pearson Education, Inc.;Upper Saddle River:
10. Nair V, Hinton GE. 2010. Rectified linear units improve restricted Boltzmann machines. Paper presented at: ICML'10: Proceedings of the 27th International Conference on International Conference on Machine Learning. Haifa, Israel; 2010 Jun 21-25. p. 807–814.
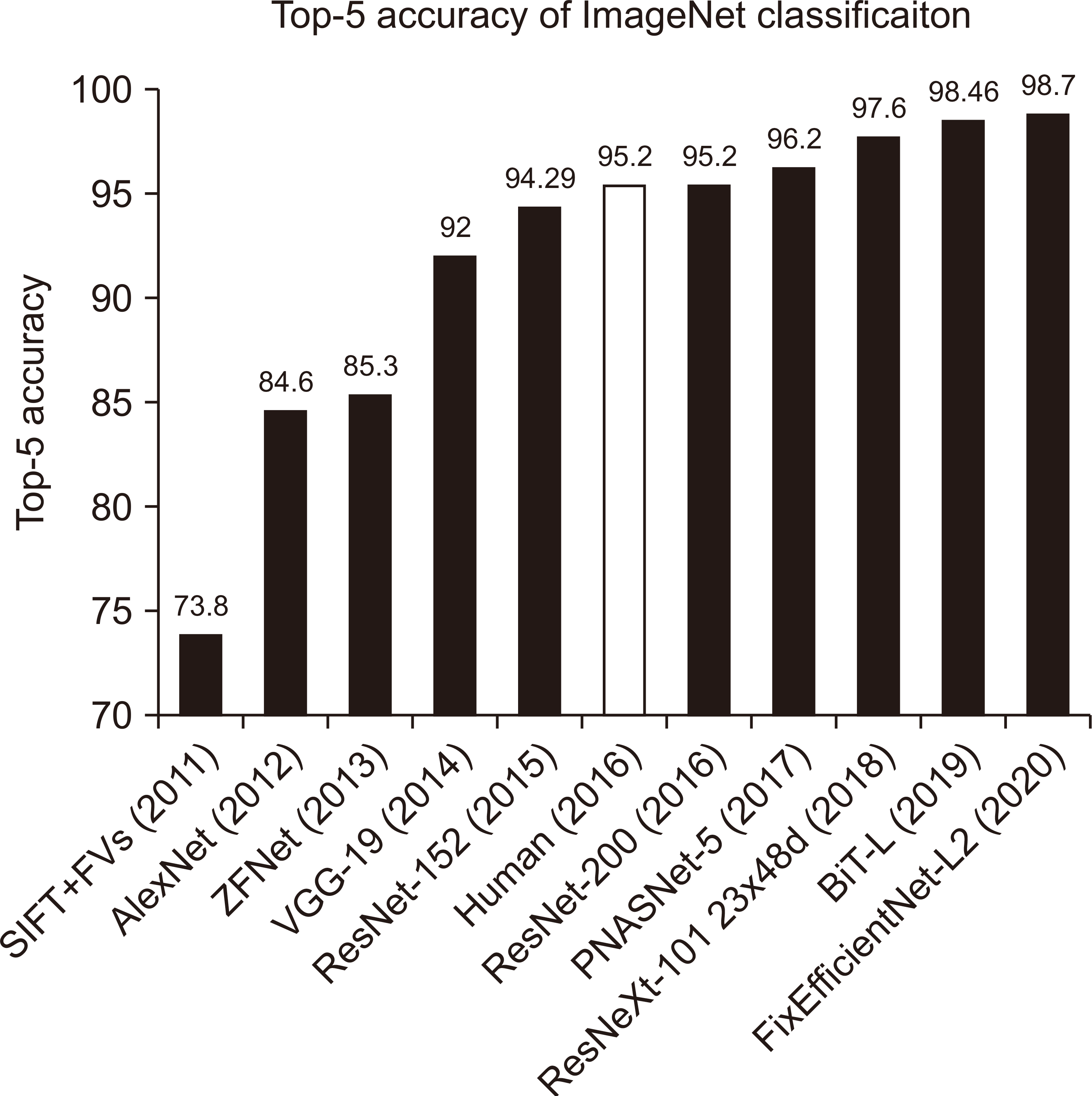
11. Krizhevsky A, Sutskever I, Hinton GE. 2012; ImageNet classification with deep convolutional neural networks. 1097–1105. PMID:
2185863.
12. He K, Zhang X, Ren S, Sun J. 2015. Deep residual learning for image recognition. arXiv.org;Ithaca: Available from:
https://arxiv.org/abs/1512.03385. cited 2020 Jul 23.
13. Goodfellow IJ, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, et al. 2014. Generative adversarial networks. arXiv.org;Ithaca: Available from:
https://arxiv.org/abs/1406.2661. cited 2020 Jul 23.
15. Gers FA, Schmidhuber J. 2000. Recurrent nets that time and count. Paper presented at: the IEEE-INNS-ENNS International Joint Conference on Neural Networks. 2000. Neural Computing: New Challenges and Perspectives for the New Millennium. Como, Italy; 2000 Jul 27. New Challenges and Perspectives for the New Millennium;Neural Computing: DOI:
10.1109/IJCNN.2000.861302.
16. Cho K, van Merrienboer B, Gulcehre C, Bahdanau D, Bougares F, Schwenk H, et al. 2014. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv.org;Ithaca: Available from:
https://arxiv.org/abs/1406.1078. cited 2020 Jul 23. DOI:
10.3115/v1/D14-1179.
17. Schuster M, Paliwal KK. 1997; Bidirectional recurrent neural networks. IEEE Trans Signal Process. 45:2673–2681. DOI:
10.1109/78.650093.

18. Krause B, Lu L, Murray I, Renals S. 2016. Multiplicative LSTM for sequence modelling. arXiv.org;Ithaca: Available from:
https://arxiv.org/abs/1609.07959. cited 2020 Jul 23.
19. Wu Y, Schuster M, Chen Z, Le QV, Norouzi M, Macherey W, et al. 2016. Google's neural machine translation system: bridging the gap between human and machine translation. arXiv.org;Ithaca: Available from:
https://arxiv.org/abs/1609.08144. cited 2020 Jul 23.
20. Cui S, Tseng HH, Pakela J, Ten Haken RK, El Naqa I. 2020; Introduction to machine and deep learning for medical physicists. Med Phys. 47:e127–e147. DOI:
10.1002/mp.14140. PMID:
32418339. PMCID:
PMC7331753.

21. Hanley J, Debois MM, Mah D, Mageras GS, Raben A, Rosenzweig K, et al. 1999; Deep inspiration breath-hold technique for lung tumors: the potential value of target immobilization and reduced lung density in dose escalation. Int J Radiat Oncol Biol Phys. 45:603–611. DOI:
10.1016/S0360-3016(99)00154-6. PMID:
10524412.

23. Ramsey CR, Scaperoth D, Arwood D, Oliver AL. 1999; Clinical efficacy of respiratory gated conformal radiation therapy. Med Dosim. 24:115–119. DOI:
10.1016/S0958-3947(99)00006-0. PMID:
10379508.

24. Shirato H, Shimizu S, Kunieda T, Kitamura K, van Herk M, Kagei K, et al. 2000; Physical aspects of a real-time tumor-tracking system for gated radiotherapy. Int J Radiat Oncol Biol Phys. 48:1187–1195. DOI:
10.1016/S0360-3016(00)00748-3. PMID:
11072178.

26. Sun WZ, Jiang MY, Ren L, Dang J, You T, Yin FF. 2017; Respiratory signal prediction based on adaptive boosting and multi-layer perceptron neural network. Phys Med Biol. 62:6822–6835. DOI:
10.1088/1361-6560/aa7cd4. PMID:
28665297. PMCID:
PMC5555420.

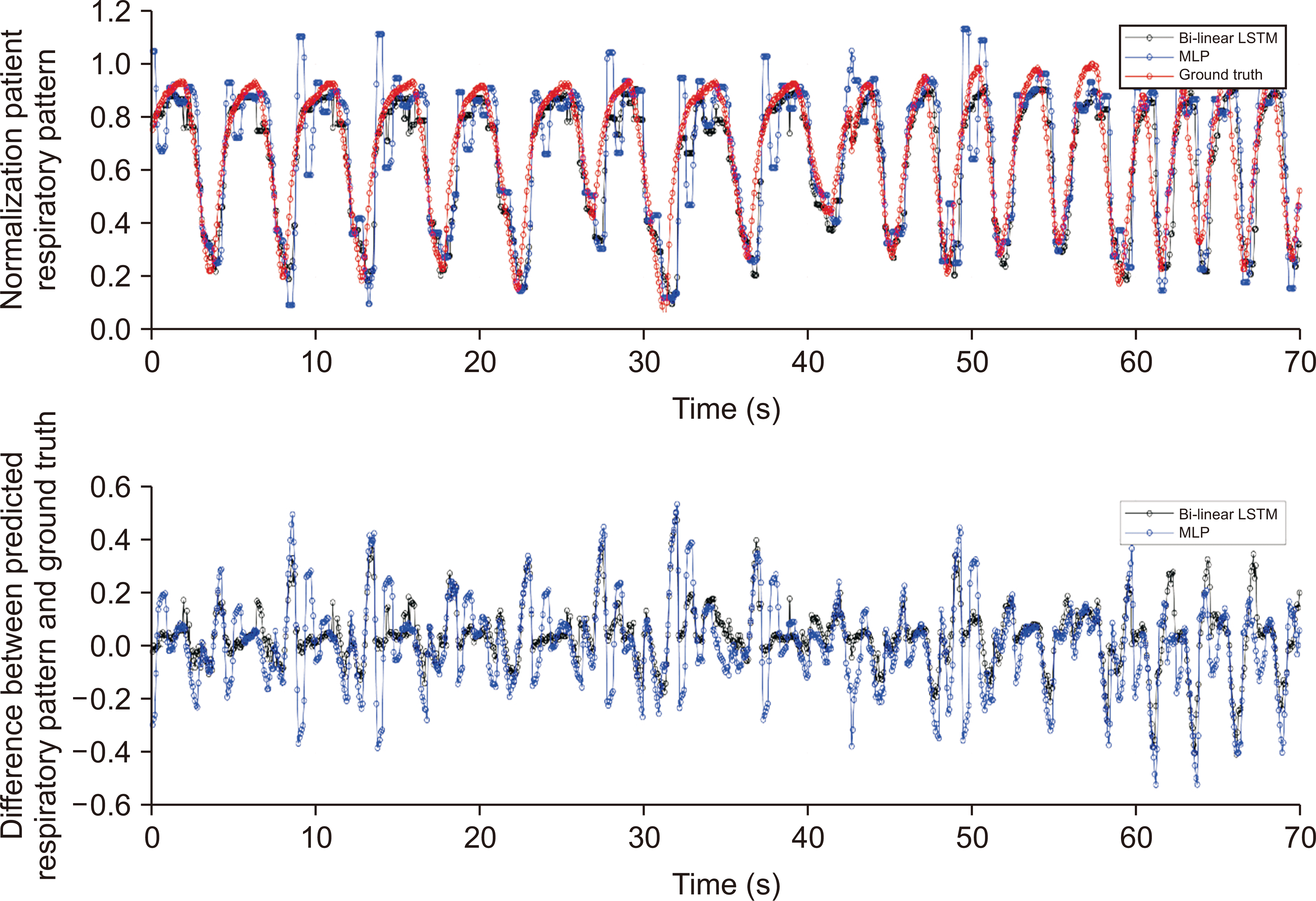
27. Wang R, Liang X, Zhu X, Xie Y. 2018; A feasibility of respiration prediction based on deep Bi-LSTM for real-time tumor tracking. IEEE Access. 6:51262–51268. DOI:
10.1109/ACCESS.2018.2869780.

28. Chaikh A, Thariat J, Thureau S, Tessonnier T, Kammerer E, Fontbonne C, et al. 2020; [Construction of radiobiological models as TCP (tumor control probability) and NTCP (normal tissue complication probability): from dose to clinical effects prediction]. Cancer Radiother. 24:247–257. French. DOI:
10.1016/j.canrad.2019.12.004. PMID:
32220563.
29. Luo Y, Chen S, Valdes G. 2020; Machine learning for radiation outcome modeling and prediction. Med Phys. 47:e178–e184. DOI:
10.1002/mp.13570. PMID:
32418338.

30. Arefan D, Mohamed AA, Berg WA, Zuley ML, Sumkin JH, Wu S. 2020; Deep learning modeling using normal mammograms for predicting breast cancer risk. Med Phys. 47:110–118. DOI:
10.1002/mp.13886. PMID:
31667873. PMCID:
PMC6980268.

32. Li H, Boimel P, Janopaul-Naylor J, Zhong H, Xiao Y, Ben-Josef E, et al. 2019; Deep convolutional neural networks for imaging data based survival analysis of rectal cancer. Proc IEEE Int Symp Biomed Imaging. 2019:846–849. DOI:
10.1109/ISBI.2019.8759301. PMID:
31929858. PMCID:
PMC6955095.

33. Tait LM, Hoffman D, Benedict S, Valicenti R, Mayadev JS. 2016; The use of MRI deformable image registration for CT-based brachytherapy in locally advanced cervical cancer. Brachytherapy. 15:333–340. DOI:
10.1016/j.brachy.2016.01.002. PMID:
26882845.

34. Qi M, Li Y, Wu A, Jia Q, Li B, Sun W, et al. 2020; Multi-sequence MR image-based synthetic CT generation using a generative adversarial network for head and neck MRI-only radiotherapy. Med Phys. 47:1880–1894. DOI:
10.1002/mp.14075. PMID:
32027027.

35. Yang C, Liu F, Ahunbay E, Chang YW, Lawton C, Schultz C, et al. 2014; Combined online and offline adaptive radiation therapy: a dosimetric feasibility study. Pract Radiat Oncol. 4:e75–e83. DOI:
10.1016/j.prro.2013.02.012. PMID:
24621436.

36. Chen L, Liang X, Shen C, Jiang S, Wang J. 2020; Synthetic CT generation from CBCT images via deep learning. Med Phys. 47:1115–1125. DOI:
10.1002/mp.13978. PMID:
31853974. PMCID:
PMC7067667.

38. Zhou Z, He Z, Jia Y. 2020; AFPNet: A 3D fully convolutional neural network with atrous-convolution feature pyramid for brain tumor segmentation via MRI images. Neurocomputing. 402:235–244. DOI:
10.1016/j.neucom.2020.03.097.

40. Rachmadi MF, Valdés-Hernández MDC, Agan MLF, Di Perri C, Komura T. Alzheimer's Disease Neuroimaging Initiative. 2018; Segmentation of white matter hyperintensities using convolutional neural networks with global spatial information in routine clinical brain MRI with none or mild vascular pathology. Comput Med Imaging Graph. 66:28–43. DOI:
10.1016/j.compmedimag.2018.02.002. PMID:
29523002.

41. Zhu W, Huang Y, Zeng L, Chen X, Liu Y, Qian Z, et al. 2019; AnatomyNet: deep learning for fast and fully automated whole-volume segmentation of head and neck anatomy. Med Phys. 46:576–589. DOI:
10.1002/mp.13300. PMID:
30480818.

42. Ahn SH, Yeo AU, Kim KH, Kim C, Goh Y, Cho S, et al. 2019; Comparative clinical evaluation of atlas and deep-learning-based auto-segmentation of organ structures in liver cancer. Radiat Oncol. 14:213. DOI:
10.1186/s13014-019-1392-z. PMID:
31775825. PMCID:
PMC6880380.

43. Quan TM, Hildebrand DGC, Jeong WK. 2016. FusionNet: a deep fully residual convolutional neural network for image segmentation in connectomics. arXiv.org;Ithaca: Available from:
https://arxiv.org/abs/1612.05360. cited 2020 Jul 23.
44. Vinod SK, Min M, Jameson MG, Holloway LC. 2016; A review of interventions to reduce inter-observer variability in volume delineation in radiation oncology. J Med Imaging Radiat Oncol. 60:393–406. DOI:
10.1111/1754-9485.12462. PMID:
27170216.

45. Rios Piedra EA, Taira RK, El-Saden S, Ellingson BM, Bui AAT, Hsu W. 2016; Assessing variability in brain tumor segmentation to improve volumetric accuracy and characterization of change. IEEE EMBS Int Conf Biomed Health Inform. 2016:380–383. DOI:
10.1109/BHI.2016.7455914. PMID:
28670648. PMCID:
PMC5489257.
46. Apolle R, Appold S, Bijl HP, Blanchard P, Bussink J, Faivre-Finn C, et al. 2019; Inter-observer variability in target delineation increases during adaptive treatment of head-and-neck and lung cancer. Acta Oncol. 58:1378–1385. DOI:
10.1080/0284186X.2019.1629017. PMID:
31271079.

47. Chabane KTW. 2018. Interobserver variation of prostate delineation on CT and MR by radiation oncologists, radiologists and urologists at the Universitas annex oncology department [dissertation]. University of the Free State;Bloemfontein:
48. Franco P, Arcadipane F, Trino E, Gallio E, Martini S, Iorio GC, et al. 2018; Variability of clinical target volume delineation for rectal cancer patients planned for neoadjuvant radiotherapy with the aid of the platform Anatom-e. Clin Transl Radiat Oncol. 11:33–39. DOI:
10.1016/j.ctro.2018.06.002. PMID:
29928706. PMCID:
PMC6008279.

49. Cabrera GG, Ehrgott M, Mason AJ, Raith A. 2018; A matheuristic approach to solve the multiobjective beam angle optimization problem in intensity-modulated radiation therapy. 25:243–268. DOI:
10.1111/itor.12241. PMID:
29928706. PMCID:
PMC6008279.
50. Breedveld S, Storchi PR, Voet PW, Heijmen BJ. 2012; iCycle: integrated, multicriterial beam angle, and profile optimization for generation of coplanar and noncoplanar IMRT plans. Med Phys. 39:951–963. DOI:
10.1118/1.3676689. PMID:
22320804.

51. Taasti VT, Hong L, Shim JSA, Deasy JO, Zarepisheh M. 2020; Automating proton treatment planning with beam angle selection using Bayesian optimization. Med Phys. 47:3286–3296. DOI:
10.1002/mp.14215. PMID:
32356335. PMCID:
PMC7429260.

52. Sadeghnejad Barkousaraie A, Ogunmolu O, Jiang S, Nguyen D. 2020; A fast deep learning approach for beam orientation optimization for prostate cancer treated with intensity-modulated radiation therapy. Med Phys. 47:880–897. DOI:
10.1002/mp.13986. PMID:
31868927.
53. Quan EM, Li X, Li Y, Wang X, Kudchadker RJ, Johnson JL, et al. 2012; A comprehensive comparison of IMRT and VMAT plan quality for prostate cancer treatment. Int J Radiat Oncol Biol Phys. 83:1169–1178. DOI:
10.1016/j.ijrobp.2011.09.015. PMID:
22704703. PMCID:
PMC3805837.

54. Hoffmann M, Pacey J, Goodworth J, Laszcyzk A, Ford R, Chick B, et al. 2019; Analysis of a volumetric-modulated arc therapy (VMAT) single phase prostate template as a class solution. Rep Pract Oncol Radiother. 24:92–96. DOI:
10.1016/j.rpor.2018.10.009. PMID:
30505239. PMCID:
PMC6251366.

55. Chen X, Men K, Li Y, Yi J, Dai J. 2019; A feasibility study on an automated method to generate patient-specific dose distributions for radiotherapy using deep learning. Med Phys. 46:56–64. DOI:
10.1002/mp.13262. PMID:
30367492.

56. Barragán-Montero AM, Nguyen D, Lu W, Lin MH, Norouzi-Kandalan R, Geets X, et al. 2019; Three-dimensional dose prediction for lung IMRT patients with deep neural networks: robust learning from heterogeneous beam configurations. Med Phys. 46:3679–3691. DOI:
10.1002/mp.13597. PMID:
31102554.
57. Galib SM, Lee HK, Guy CL, Riblett MJ, Hugo GD. 2020; A fast and scalable method for quality assurance of deformable image registration on lung CT scans using convolutional neural networks. Med Phys. 47:99–109. DOI:
10.1002/mp.13890. PMID:
31663137.

58. Nyflot MJ, Thammasorn P, Wootton LS, Ford EC, Chaovalitwongse WA. 2019; Deep learning for patient-specific quality assurance: identifying errors in radiotherapy delivery by radiomic analysis of gamma images with convolutional neural networks. Med Phys. 46:456–464. DOI:
10.1002/mp.13338. PMID:
30548601.

59. Interian Y, Rideout V, Kearney VP, Gennatas E, Morin O, Cheung J, et al. 2018; Deep nets vs expert designed features in medical physics: an IMRT QA case study. Med Phys. 45:2672–2680. DOI:
10.1002/mp.12890. PMID:
29603278.

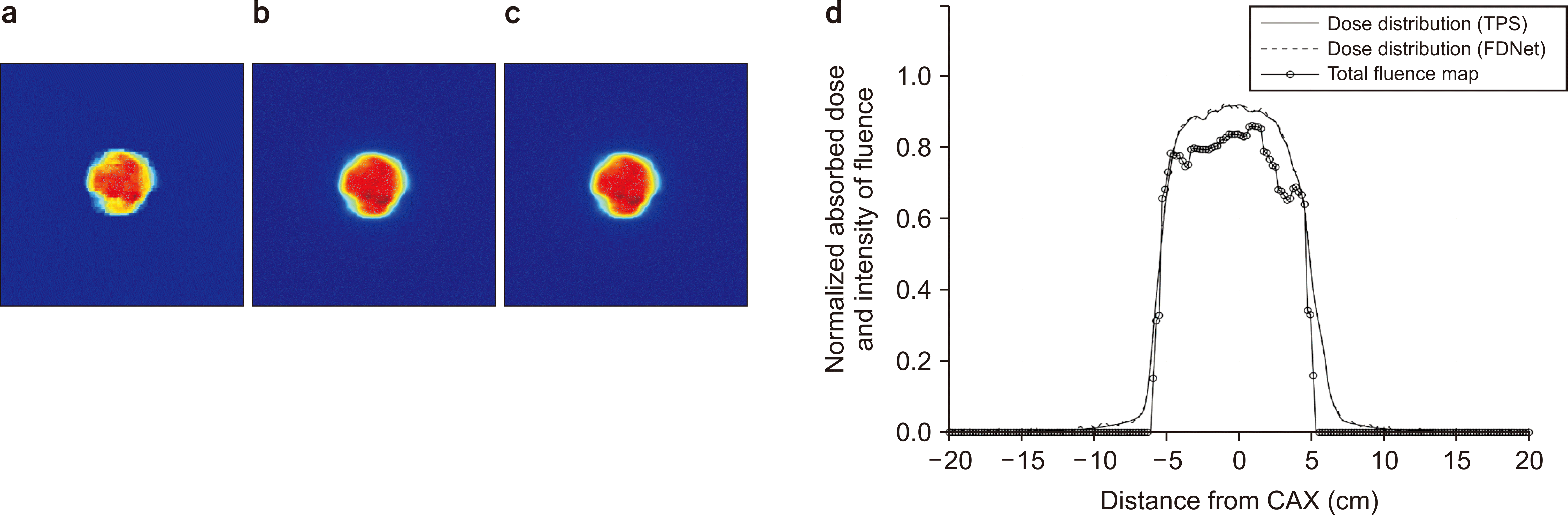
60. Cheon W, Kim SJ, Hwang UJ, Min BJ, Han Y. 2019; Feasibility study of the fluence-to-dose network (FDNet) for patient-specific IMRT quality assurance. J Korean Phys Soc. 75:724–734. DOI:
10.3938/jkps.75.724.

61. Kim KH, Do WJ, Park SH. 2018; Improving resolution of MR images with an adversarial network incorporating images with different contrast. Med Phys. 45:3120–3131. DOI:
10.1002/mp.12945. PMID:
29729006.
62. Chun J, Zhang H, Gach HM, Olberg S, Mazur T, Green O, et al. 2019; MRI super-resolution reconstruction for MRI-guided adaptive radiotherapy using cascaded deep learning: in the presence of limited training data and unknown translation model. Med Phys. 46:4148–4164. DOI:
10.1002/mp.13717. PMID:
31309585.

63. Cheon W, Lee J, Min BJ, Han Y. 2019; Super-resolution model for high-precision in vivo proton range verification using a stereo gamma camera: a feasibility study. J Korean Phys Soc. 75:617–627. DOI:
10.3938/jkps.75.617.

64. Lu Y, Kowarschik M, Huang X, Xia Y, Choi JH, Chen S, et al. 2019; A learning-based material decomposition pipeline for multi-energy x-ray imaging. Med Phys. 46:689–703. DOI:
10.1002/mp.13317. PMID:
30508253.

65. Cheon W, Kim SJ, Kim K, Lee M, Lee J, Jo K, et al. 2019; Feasibility of two-dimensional dose distribution deconvolution using convolution neural networks. Med Phys. 46:5833–5847. DOI:
10.1002/mp.13869. PMID:
31621917.





 PDF
PDF Citation
Citation Print
Print




 XML Download
XML Download