Review of the Existing Relative Biological Effectiveness Models for Carbon Ion Beam Therapy

Yejin Kim; Jinsung Kim; Seungryong Cho

doi:10.14316/pmp.2020.31.1.1

Journal List > Prog Med Phys > v.31(1) > 1145680

Go to TopGo to Top Go to BottomGo to Bottom

TOOLS

Kim, Kim, and Cho: Review of the Existing Relative Biological Effectiveness Models for Carbon Ion Beam Therapy

Review Article

Progress in Medical Physics 2020;31(1):1-7.

Published online: 31 March 2020

DOI: https://doi.org/10.14316/pmp.2020.31.1.1

Review of the Existing Relative Biological Effectiveness Models for Carbon Ion Beam Therapy

Yejin Kim¹

, Jinsung Kim²

, Seungryong Cho¹

¹Department of Nuclear and Quantum Engineering, Korea Advanced Institute of Science and Technology, Daejeon,

²Department of Radiation Oncology, Yonsei Cancer Center, Yonsei University College of Medicine, Seoul, Korea

Corresponding author Seungryong Cho (scho@kaist.ac.kr) Tel: 82-42-350-3828 Fax: 82-42-350-3810

Received 6 January 2020 Revised 9 March 2020 Accepted 9 March 2020

(open-access):

This is an open-access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

Hadron therapy, such as carbon and helium ions, is increasingly coming to the fore for the treatment of cancers. Such hadron therapy has several advantages over conventional radiotherapy using photons and electrons physically and clinically. These advantages are due to the different physical and biological characteristics of heavy ions including high linear energy transfer and Bragg peak, which lead to the reduced exit dose, lower normal tissue complication probability and the increased relative biological effectiveness (RBE). Despite the promising prospects on the carbon ion radiation therapy, it is in dispute with which bio-mathematical models to calculate the carbon ion RBE. The two most widely used models are local effect model and microdosimetric kinetic model, which are actively utilized in Europe and Japan respectively. Such selection on the RBE model is a crucial issue in that the dose prescription for planning differs according to the models. In this study, we aim to (i) introduce the concept of RBE, (ii) clarify the determinants of RBE, and (iii) compare the existing RBE models for carbon ion therapy.

Keywords: Carbon ion radiotherapy, Relative biological effectiveness, Local effect model, Microdosimetric kinetic model

Introduction

Hadron therapy, such as carbon and helium ions, is increasingly coming to the fore for the treatment of cancers [1]. Such hadron therapy has several advantages over conventional radiotherapy using photons and electrons physically and clinically [2]. These advantages are due to the different physical and biological characteristics of heavy ions including high liner energy transfer (LET) and Bragg peak, which lead to the reduced exit dose, lower normal tissue complication probability and the increased relative biological effectiveness (RBE) [2-4]. The physical depth-dose distribution of hadrons is characterized by a low entrance dose and an intensively high dose (Bragg peak) near the edge of their range with sharp fall-off at the distal region. The distinctively low entrance and exit doses are beneficial for sparing normal tissues, while the high dose at the Bragg peak is optimal for targeting solid tumors [5]. Furthermore, enhanced biological effectiveness near the Bragg peak by concentrated ionization results in more double strand breaks (DSB) and less repairs in a target organ. Among the hadrons, carbon ions show superior preclinical and clinical results than the protons. This is because the carbon ions have higher RBE, sharper dose distribution and minimal penumbra than protons [6]. Based on these therapeutically beneficial aspects of carbon ions, there are 13 carbon ion therapy facilities in clinical operations and 6 facilities under constructions including 2 facilities in South Korea in Dec 2019 according to the Particle Therapy Co-Operative Group. Likewise, there is an internationally growing number of clinical trials involving carbon ion radiation therapy since the first trial in June 1994 in Heavy Ion Medical Accelerator in China Japan [7,8]. There has been 63 ongoing clinical trials until Dec 2018 and 19 newly registered trials from Jan 2019 [9]. Despite the promising prospects on the carbon ion radiation therapy, it is in dispute with which bio-mathematical models to calculate the carbon ion RBE. The two most widely used models are local effect model and microdosimetric kinetic model, which are actively utilized in Heidelberg Ion Beam Therapy Center in Europe and National Institute of Radiological Science in Japan respectively. Such selection on the RBE model is a crucial issue in that the dose prescription for planning differs according to the models. In this study, we aim to (i) introduce the concept of RBE, (ii) clarify the determinants of RBE, and (iii) compare the existing RBE models for carbon ion therapy.

Relative Biological Effectiveness

1. Concept of relative biological effectiveness

For a given identical absorbed dose, irradiations with ion beams are biologically more effective than that with conventional photons. In other words, ion beam requires less physical dose than the photon beam in order to have the same biological effect. This elevated effectiveness of ion beam is described as a multiplication factor:

(1)

d_{ph} = RBE \cdot d_{ion}

Where d_ph and d_ion are the isoeffective photon dose and the ion dose respectively. In clinics, despite the rising demand for the more sophisticate calculation, the RBE for proton beam is fixed to 1.1. However, the RBE values for the carbon ion beam vary approximately from 1 to 10 depending on dose, beam quality, and biological factors [10]. Therefore, the carbon ion RBE should be carefully calculated so as to minimize the planning error. In order to calculate the RBE, a biological endpoint should be designated. There are several candidates for the biological endpoints including cell survival, normal tissue complication probabilities and tumor growth delay, whilst using the cell survival most commonly. The selection of the biological endpoint for the radiotherapy is delineated in details elsewhere [11,12].

2. Derivation

Given equation (1), the RBE can be rewritten as following:

(2)

RBE = \frac{d_{ph}}{d_{ion}} |_{isoeffect}

With the cell survival as a biological endpoint, the relationship between cell survival and delivered dose is formularized in Linear Quadratic (LQ) model [13].

(3)

lnS = - α d - β d^{2}

Where S is the survival probability, d is the delivered dose, and α and β are the parameters describing the cell’s radiosensitivity. Expecting to have the same cell survival from a single fraction of radiation each,

(4)

- lnS = α_{ion} d_{ion} + β_{ion} d_{ion}^{2} = α_{ph} d_{ph} + β_{ph} d_{ph}^{2}

Where α_ion and β_ion are the parameters for beam type ion. By rearranging the equation (4), the ion dose can be rewritten as following:

(5)

\begin{matrix} α_{ion} d_{ion} + β_{ion} d_{ion}^{2} = β_{ion} {(d_{ion} - \frac{α_{ion}}{{2 β}_{ion}})}^{2} - \frac{α_{ion}^{2}}{{4 β}_{ion}^{2}} = α_{ph} d_{ph} + β_{ph} d_{ph}^{2} \\ d_{ion} = \sqrt{\frac{α_{ion}^{2}}{{4 β}_{ion}^{2}} + \frac{α_{ph} d_{ph} + β_{ph} d_{ph}^{2}}{β_{ion}}} + \frac{α_{ion}}{{2 β}_{ion}} \end{matrix}

Likewise, the isoeffective photon dose is,

(6)

d_{ph} = \sqrt{\frac{α_{ph}^{2}}{{4 β}_{ph}^{2}} + \frac{α_{ion} d_{ion} + β_{ion} d_{ion}^{2}}{β_{ph}}} + \frac{α_{ph}}{{2 β}_{ph}}

Using the equations (5) and (6), the RBE is,

(7a)

RBE = \frac{d_{ph}}{d_{ion}} |_{isoeffect} = \frac{{RBE}_{\max} + \sqrt{{RBE}_{\max}^{2} + {4 RBE}_{\max} d_{ph} [1 + \frac{d_{ph}}{{(α / β)}_{ph}}] / {(α / β)}_{ion}}}{2 (1 + \frac{d_{ph}}{{(α / β)}_{ph}})}

(7b)

= \frac{{- (α / β)}_{ph} + \sqrt{{(α / β)}_{ph}^{2} + {4 (α / β)}_{ph} {RBE}_{\max} d_{ion} [1 + \frac{d_{ion}}{{(α / β)}_{ion}}]}}{{2 d}_{ion}}

(7c)

= \frac{\sqrt{{(α / β)}_{ph}^{2} + {4 d}_{ion} {(α / β)}_{ion} {RBE}_{\max} + {4 RBE}_{\min}^{2} d_{ion}^{2}} - {(α / β)}_{ph}}{{2 d}_{ion}}

With

{RBE}_{\max} \equiv α_{ion} / α_{ph}

the maximum RBE or the initial slope of the cell survival curve and

{RBE}_{\min} \equiv \sqrt{β_{ion} / β_{ph}}

the asymptotic RBE at high doses. The three transfigurations for RBE, which are (7a), (7b), and (7c), are for the diverse applications in clinical calculation.

Determinants of Relative Biological Effectiveness

Carbon ion RBE is determined by complex factors; particle energy, doses, cell types, and even patient’s radioresistance [14]. However, none of them are able to be estimated perfectly, leaving wide range of research fields to be explored. In this chapter, we specify three most significant determinants that affect to the carbon ion RBE and point out the limitations of the determinants.

1. Linear energy transfer

For ion beam therapy, linear energy transfer (LET) is usually used to quantify the beam quality. LET is the amount of energy that an ionizing particle transfers to the material traversed per unit distance. The main rationales for the therapeutic applications of carbon ion beam are high LET near the Bragg peak region and low LET in the entrance and exit region. Since the LET is uniquely defined for a single beam energy, use of an average value over energy spectrum of the carbon ion beam is inevitable. The average LET is either the fluence-averaged LET (LET_f) or dose-averaged LET.

(8a)

{LET}_{f} (z) = \frac{\sum_{i} \int_{0}^{\infty} S_{i} (E) ϕ_{i} (E, z) d E}{\sum_{i} \int_{0}^{\infty} ϕ_{i} (E, z) d E}

(8b)

{LET}_{d} (z) = \frac{\sum_{i} \int_{0}^{\infty} S_{i} (E) d_{i} (E, z) d E}{\sum_{i} \int_{0}^{\infty} d_{i} (E, z) d E}

Where z is the location, S_i is the stopping power of the specific particle i, ϕ is the particle fluence with energy E, and d is the respective dose. Since these two distinctive average types turn in different LET value, it is important to indicate which definition of the average LET refer to. The dose-averaged LET is generally adopted in clinical situation. However the validity of using dose-averaged LET for all applications is controversial. Especially in case of broad LET distributions, for example the spread-out Bragg peaks, LET_d is not sufficiently accurate for the carbon ion RBE [15]. In case of monoenergetic beam, LET_f is of course identical to LET_d , but this is not applicable for some clinical environments.

2. Biological end-point

Given the same beam species, RBE still can shift along with biological end-point, dose. Generally, RBE increases with decreasing dose. Nevertheless, the comparison condition should be clearly mentioned. For example, fixing the cell survival probability, the higher fraction number leads to higher increase in tolerance doses for photons than carbon ion. This, in turn, leads to the higher RBE with lower fractional dose (Fig. 1). On the other hand, fixing the fraction number, the survival curve of the LQ model for carbon ion beam reveals to be steeper than for photons. Thereby, the RBE rises with the decreasing dose in this condition.

3. Biological factors

Any biological factor that influences the response of the biological system will change the RBE. For example, various cell type, intrinsic radioresistance, and fractionation dependence are the candidates for biological factors to impact the RBE. Although these biological factors play in different mechanisms, some of them can be represented by α and β, the parameters of the LQ model [16-18]. The parameters α and β basically consider two different types of cell killing mechanisms: single and multiple hit of radiation. However, these parameters have intrinsic limitations in that they were derived from in-vitro experiments in a well-controlled condition which may be off the in-vivo clinical condition. Likewise, they cannot count for the diversity among the patient population nor the diversity within an individual.

Existing Relative Biological Effectiveness Models

1. Local effect model

1) Versions of local effect model

The first version of local effect model (LEM) was suggested in a stochastic framework by Scholz et al. [19] Since the first version in 1997, succeeding improvements were made to the model. The LEM is widely used for estimating the RBE in Europe for the carbon ion radiotherapy. The predictions from LEM I were reasonably compatible with experimental and clinical data. However, relatively high errors have been observed for high-energy and low-LET particles when using the model parameters. Therefore, LEM II were suggested to improve the predictions. In the second version, cluster effects of single strand breaks (SSBs) at the nanometer scale were taken into account. The clusters of SSBs consisting of individual SSBs spacing less than 25 base-pairs were considered as additional DSBs [20]. A further development was added to the existing LEM counting for more sophisticated track structure description, and this model is named LEM III [21]. In the most recent version LEM IV, the relationship between the final biological response and the initial spatial DNA damage distribution was explicitly explained [22,23]. Although the LEM has thus been improved, the LEM I is still in the clinical use while the others remain in an experimental stage [2-10].

2) Local effect model I

LEM I considers the local biological effects as a function of the ’local dose’ deposited by the charged particle tracks. Based on the measurable quantities like the X-ray survival curve, the radial dose profile within a track and a geometrical description of the cell nucleus, the LEM I suggests that the carbon ion RBE is formulated as a function of energy and atomic number of the particles. The LEM I uses the ’amorphous’ track structure approach, which will be discussed in this chapter [24,25].

The ‘local dose’ is an important concept for understanding LEM I. The main assumption of the LEM I is that the biological effect is utterly determined by the spatial local dose distribution inside the cell nucleus, regardless of the particle species either photons or heavy ions. In other words, the local dose distribution decides the biological effect within a cell nucleus eventually including the entire cell’s fate. It is assumed that the cell nucleus is homogenously filled with sensitive sites, i.e. DNAs. Dividing the cell nucleus volume V into multiple small subvolumes, one assigns a single subvolume to have a typical threshold value of damage, called a lethal damage. It is considered that a cell survives from irradiation only when none of the subvolumes within the cell nucleus received damage exceeding the threshold (lethal) damage.

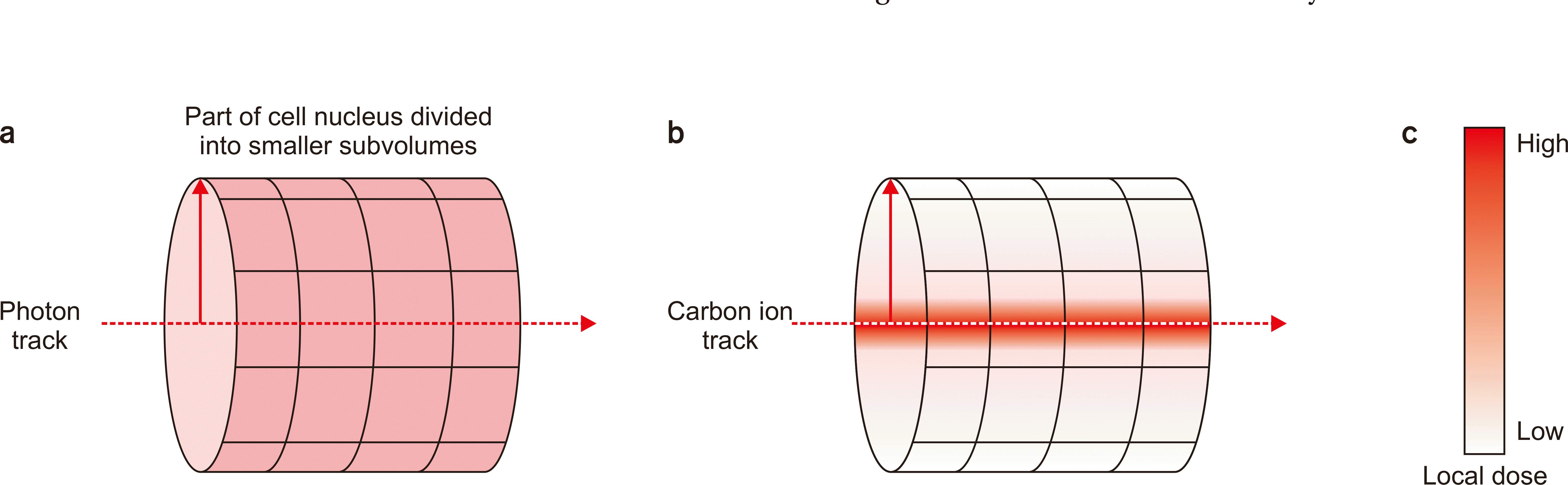
The amorphous track structure of the carbon ion irradiation is another critical aspect of LEM I. A comparison to the track structure of the photon irradiation is useful for understanding the carbon ion track structure. A photon interacts uniformly along the radial profile of the beam track within a cell nucleus, whereas a carbon ion has inhomogeneous interactions along the radial profile, approximately following the 1/r² rule. Then, the local dose distribution of carbon ion beam LD_ion (r) along the radial direction r is,

(9)

{LD}_{ion} (r) = {\begin{matrix} λ LET / r_{\min}^{2} & r < r_{\min} \\ λ LET / r^{2} & r_{\min} \leq r < r_{\max} \\ 0 & r_{\max} \end{matrix}

where λ is a normalization constant, r_min and r_max are cutoff parameters. The local dose distribution of photon beam LD_ph , however, is rather constant along r.

Considering this differences in track structure between photons and carbon ions, the biological effect within the cell nucleus, thus the cell fate after irradiation, will be drastically different. Even if the same total absorbed dose was given to a cell nucleus, a cell with a carbon ion irradiation would get more chances to have subvolumes with lethal damage because of the carbon ion track structure. Meanwhile, a cell nucleus irradiated with a photon receives uniform low local dose over the given volume, having no chance to make lethal damage (Fig. 2).

Then, a linear quadratic model is used to explain the cell survival curve for irradiation. The quadratic shape of the curve changes back to linear form beyond a certain transition dose D_t in LEM I. The determination of transition dose D_t is challenging since it requires cell survival experiments at very high doses.

2. Microdosimetric kinetic model

While LEM I assumes a continuous radial profile given a track position of the carbon ion, the microdosimetric kinetic model (MKM) follows microdosimetric principles. The MKM is grounded on the framework of the theory of dual radiation action (TDRA), suggested by Kellerer and Rossi in 1978 [26]. Based on the TDRA, the MKM is a specifically designed statistical model for the carbon ion RBE [27]. The MKM is mainly used in Japan for carbon ion radiotherapy.

1) Theory of dual radiation action

Dual radiation action deals with a process referring to the cellular lesions produced after ionizing irradiation. It states that, depending on the pattern of energy transfers to the cell, ’sublesions’ are produced after irradiation. These sublesions can interacts each other so as to produce ’lesions’ within a cell, which in turn determines the cell fate. In short, pairs of sublesions can combine to form a lesion.

It is assumed that the cell nucleus have a number of smaller regions called ’loci’, and a volume heavily occupied by many loci is termed to the ’sensitive matrix’. That is, a region with a collective loci is called sensitive matrix in a cell nucleus. The sensitive matrix is rather randomly distributed over a cell nucleus. A sublesion can be formed when an energy transfer from irradiation to a cell happens within a locus. Any pairs of sublesions within a single sensitive matrix can interact to form a lesion. The possibility to generate a lesion decreases as the distance between sublesions increases. Thus, it is more likely to form a lesion when the energy transfer is intensively concentrated within small region.

2) Microdosimetric kinetic model

Based on the concept of TDRA, the MKM provides a statistical way to derive the carbon ion RBE. The cell nucleus is regarded as a collection of compartments, called domains. A pair of potentially lethal lesions can develop to form a lethal lesion only when they are in the same domain. Domains share a common mass and volume, filling the cell nucleus without vacancy.

The derivation of carbon ion RBE in MKM framework begins with a statement that a probability of a particle to interact within a domain follows Poisson distribution,

(10)

P (j, µ) = \frac{e^{- µ} µ^{j}}{j!},

where j is the number of interactions within a domain and µ is the mean number of interactions per domain. Followed by statistical derivations, the cell survival fraction from carbon ion irradiations can be represented by

(11)

- lnS = α_{app} G + {βG}^{2}

(12)

α_{app} = α_{0} + γ β,

where G is an average absorbed carbon ion dose within a cell nucleus, α₀ refers to the limiting value of α as the LET approaches zero, and γ is a newly added parameter. By substituting Eq. (11) to Eq. (4) and re-arranging, one can write the carbon ion RBE by

(13)

RBE = \frac{\sqrt{α^{2} + 4 β S *} - α}{\sqrt{α_{app}^{2} + 4 β S *} - α_{app}}

, where S* is the negative of natural log of the chosen reference survival fraction. More detailed derivations are well explained elsewhere [27]. Here, γ characterizes the beam quality and is related to the variance of the microscopic energy deposition to the domains and the whole nucleus. Also, β is considered an intrinsic independent variable of the beam quality since the beam quality is fully characterized by the parameter γ.

Importantly, a phenomena called 'overkill effect' has later been considered by Kase et al. [28] in 2006. This effect is also called 'saturation effect', which counts for the interaction probability approaching a maximum value at large values of dose while being proportional to square of dose at low levels [28,29].

Conclusions

In this brief review article, we summarized the general concept of carbon ion RBE, specified the determinants of RBE, and explained the theories and interpretations of two existing RBE models: local effect model and microdosimetric kinetic model. There is an explosively increasing number of studies referring the carbon ion RBE. This adversely shows the demand on more comprehensively standardized estimation of the carbon ion RBE. As the carbon ion RBE models evolved rather separately in Europe and Japan, with their clinical trials in isolation to each other, the global randomized clinical trials are lacking. More comprehensive solution to the current challenge regarding the carbon ion RBE and clinical trials would, therefore, be highly desirable.

ACKNOWLEDGMENTS

Notes

Conflicts of Interest

The authors have nothing to disclose.

Availability of Data and Materials

All relevant data are within the paper and its Supporting Information files.

Author Contributions

Conceptualization: Yejin Kim, Jinsung Kim and Seungryong Cho. Investigation: Yejin Kim. Supervision: Jinsung Kim, Seungryong Cho. Visualization: Yejin Kim. Writing–original draft: Yejin Kim. Writing–review & editing: Jinsung Kim, Seungryong Cho.

REFERENCES

1. Durante M, Debus J. 2018; Heavy charged particles: does improved precision and higher biological effectiveness translate to better outcome in patients? Semin Radiat Oncol. 28:160–167. DOI: 10.1016/j.semradonc.2017.11.004. PMID: 29735192.

2. Karger CP, Peschke P. 2017; RBE and related modeling in carbon-ion therapy. Phys Med Biol. 63:01TR02. DOI: 10.1088/1361-6560/aa9102. PMID: 28976361.

3. Fossati P, Matsufuji N, Kamada T, Karger CP. 2018; Radiobiological issues in prospective carbon ion therapy trials. Med Phys. 45:e1096–e1110. DOI: 10.1002/mp.12506. PMID: 30421806.

4. Loeffler JS, Durante M. 2013; Charged particle therapy--optimization, challenges and future directions. Nat Rev Clin Oncol. 10:411–424. DOI: 10.1038/nrclinonc.2013.79. PMID: 23689752.

5. Wang T, Xiao P, Jia S, Yuan K, Yang H. 2014; [The basic structure of heavy-ion tumor therapy facility]. Zhongguo Yi Liao Qi Xie Za Zhi. 38:427–429, 438. Chinese. PMID: 25980131.

6. Ebner DK, Kamada T. 2016; The emerging role of carbon-ion radiotherapy. Front Oncol. 6:140. DOI: 10.3389/fonc.2016.00140. PMID: 27376030. PMCID: PMC4894867.

7. Mohamad O, Makishima H, Kamada T. 2018; Evolution of carbon ion radiotherapy at the National Institute of Radiological Sciences in Japan. Cancers (Basel). 10:E66. DOI: 10.3390/cancers10030066. PMID: 29509684. PMCID: PMC5876641.

8. Lazar AA, Schulte R, Faddegon B, Blakely EA, Roach M 3rd. 2018; Clinical trials involving carbon-ion radiation therapy and the path forward. Cancer. 124:4467–4476. DOI: 10.1002/cncr.31662. PMID: 30307603. PMCID: PMC6540799.

9. World Health Organization. International Clinical Trials Registry Platform Search Portal. Geneva: World Health Organization. Available from: http://apps.who.int/trialsearch/default.aspx . [cited 2020 Jan 6].

10. Grün R, Friedrich T, Elsässer T, Krämer M, Zink K, Karger CP, et al. 2012; Impact of enhancements in the local effect model (LEM) on the predicted RBE-weighted target dose distribution in carbon ion therapy. Phys Med Biol. 57:7261–7274. DOI: 10.1088/0031-9155/57/22/7261. PMID: 23075883.

11. Bentzen SM, Parliament M, Deasy JO, Dicker A, Curran WJ, Williams JP, et al. 2010; Biomarkers and surrogate endpoints for normal-tissue effects of radiation therapy: the importance of dose-volume effects. Int J Radiat Oncol Biol Phys. 76(3(Suppl)):S145–S150. DOI: 10.1016/j.ijrobp.2009.08.076. PMID: 20171510. PMCID: PMC3431963.

12. Lühr A, von Neubeck C, Krause M, Troost EGC. 2018; Relative biological effectiveness in proton beam therapy - current knowledge and future challenges. Clin Transl Radiat Oncol. 9:35–41. DOI: 10.1016/j.ctro.2018.01.006. PMID: 29594249. PMCID: PMC5862688.

13. McMahon SJ. 2018; The linear quadratic model: usage, interpretation and challenges. Phys Med Biol. 64:01TR01. DOI: 10.1088/1361-6560/aaf26a. PMID: 30523903.

14. Schlaff CD, Krauze A, Belard A, O’Connell JJ, Camphausen KA. 2014; Bringing the heavy: carbon ion therapy in the radiobiological and clinical context. Radiat Oncol. 9:88. DOI: 10.1186/1748-717X-9-88. PMID: 24679134. PMCID: PMC4002206.

15. Grün R, Friedrich T, Traneus E, Scholz M. 2019; Is the dose-averaged LET a reliable predictor for the relative biological effectiveness? Med Phys. Phys Med Biol. 46:1064–1074. DOI: 10.1002/mp.13347. PMID: 30565705.

16. Stavrev P, Stavreva N, Ruggieri R, Nahum A. 2015; On differences in radiosensitivity estimation: TCP experiments versus survival curves. a theoretical study. a theoretical study. 60:N293–N299. DOI: 10.1088/0031-9155/60/15/N293. PMID: 26215150.

17. Abolfath R, Peeler CR, Newpower M, Bronk L, Grosshans D, Mohan R. 2017; A model for relative biological effectiveness of therapeutic proton beams based on a global fit of cell survival data. Sci Rep. 7:8340. DOI: 10.1038/s41598-017-08622-6. PMID: 28827691. PMCID: PMC5567137.

18. Glatstein E. 2011; The omega on alpha and beta. Int J Radiat Oncol Biol Phys. 81:319–320. DOI: 10.1016/j.ijrobp.2011.01.011. PMID: 21871342.

19. Scholz M, Kellerer AM, Kraft-Weyrather W, Kraft G. 1997; Computation of cell survival in heavy ion beams for therapy. the model and its approximation. Radiat Environ Biophys. 36:59–66. DOI: 10.1007/s004110050055. PMID: 9128899.

20. Elsässer T, Scholz M. 2007; Cluster effects within the local effect model. Radiat Res. 167:319–329. DOI: 10.1667/RR0467.1. PMID: 17316069.

21. Elsässer T, Krämer M, Scholz M. 2008; Accuracy of the local effect model for the prediction of biologic effects of carbon ion beams in vitro and in vivo. Int J Radiat Oncol Biol Phys. 71:866–872. DOI: 10.1016/j.ijrobp.2008.02.037. PMID: 18430521.

22. Elsässer T, Weyrather WK, Friedrich T, Durante M, Iancu G, Krämer M, et al. 2010; Quantification of the relative biological effectiveness for ion beam radiotherapy: direct experimental comparison of proton and carbon ion beams and a novel approach for treatment planning. Int J Radiat Oncol Biol Phys. 78:1177–1183. DOI: 10.1016/j.ijrobp.2010.05.014. PMID: 20732758.

23. Stewart RD, Carlson DJ, Butkus MP, Hawkins R, Friedrich T, Scholz M. 2018; A comparison of mechanism-inspired models for particle relative biological effectiveness (RBE). Med Phys. 45:e925–e952. DOI: 10.1002/mp.13207. PMID: 30421808.

24. Scholz M, Kraft G. 1996; Track structure and the calculation of biological effects of heavy charged particles. Adv Space Res. 18:5–14. DOI: 10.1016/0273-1177(95)00784-C. PMID: 11538986.

25. Elsässer T, Cunrath R, Krämer M, Scholz M. 2008; Impact of track structure calculations on biological treatment planning in ion radiotherapy. New J Phys. 10:075005. DOI: 10.1088/1367-2630/10/7/075005.

26. Kellerer AM, Rossi HH. 2012; A generalized formulation of dual radiation action. Radiat Res. 178:AV204–AV213. DOI: 10.1667/RRAV17.1. PMID: 22870971.

27. Hawkins RB. 1994; A statistical theory of cell killing by radiation of varying linear energy transfer. Radiat Res. 140:366–374. DOI: 10.2307/3579114. PMID: 7972689.

28. Kase Y, Kanai T, Matsumoto Y, Furusawa Y, Okamoto H, Asaba T, et al. 2006; Microdosimetric measurements and estimation of human cell survival for heavy-ion beams. Radiat Res. 166:629–638. DOI: 10.1667/RR0536.1. PMID: 17007551.

29. Inaniwa T, Furukawa T, Kase Y, Matsufuji N, Toshito T, Matsumoto Y, et al. 2010; Treatment planning for a scanned carbon beam with a modified microdosimetric kinetic model. Phys Med Biol. 55:6721–6737. DOI: 10.1088/0031-9155/55/22/008. PMID: 21030747.

Fig. 1

Schematic illustration of the cell survival curve based on the LQ model (2). The Survival fraction is in log scale. The photons and carbon ions are considered to be isoeffective when the survival fractions are identical. The ratio of isoeffective photon and ion dose is determined to be RBE. For instance, fixing the survival fraction to 10%, carbon ion RBE is 2.82 whereas fixing to 1%, respective RBE is 2.25. RBE, relative biological effectiveness; LQ, Linear Quadratic.

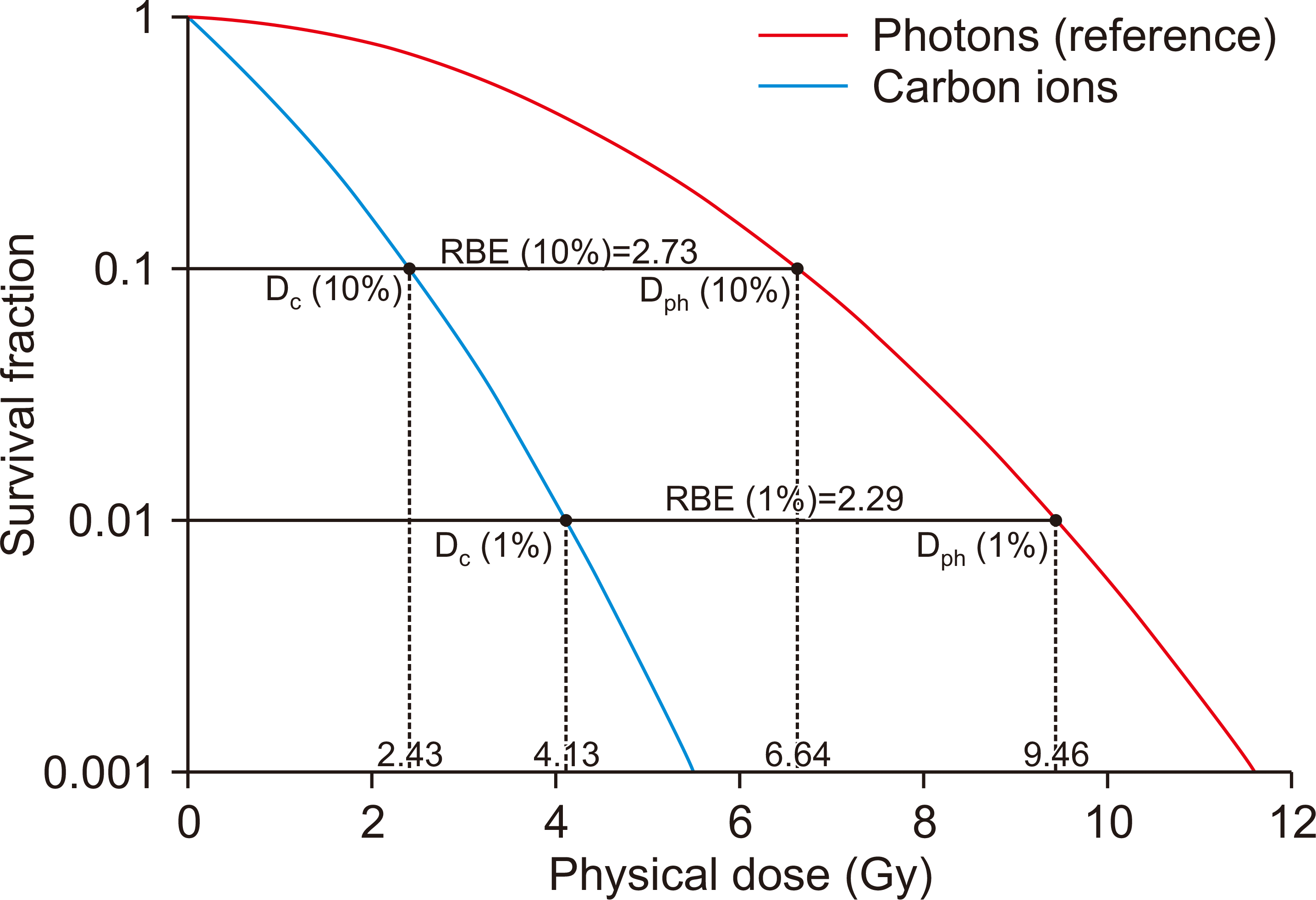
Fig. 2

Illustration of the track structure of photons and carbon ions. (a) Photon track structure within a part of cell nucleus divided into smaller subvolumes. The local dose is identical along the radial direction, denoted as a red straight line. (b) Carbon ion track structure indicates amorphous shape along the radial direction. (c) A scale bar indicates high local dose when red and zero dose when white.

TOOLS

Similar articles