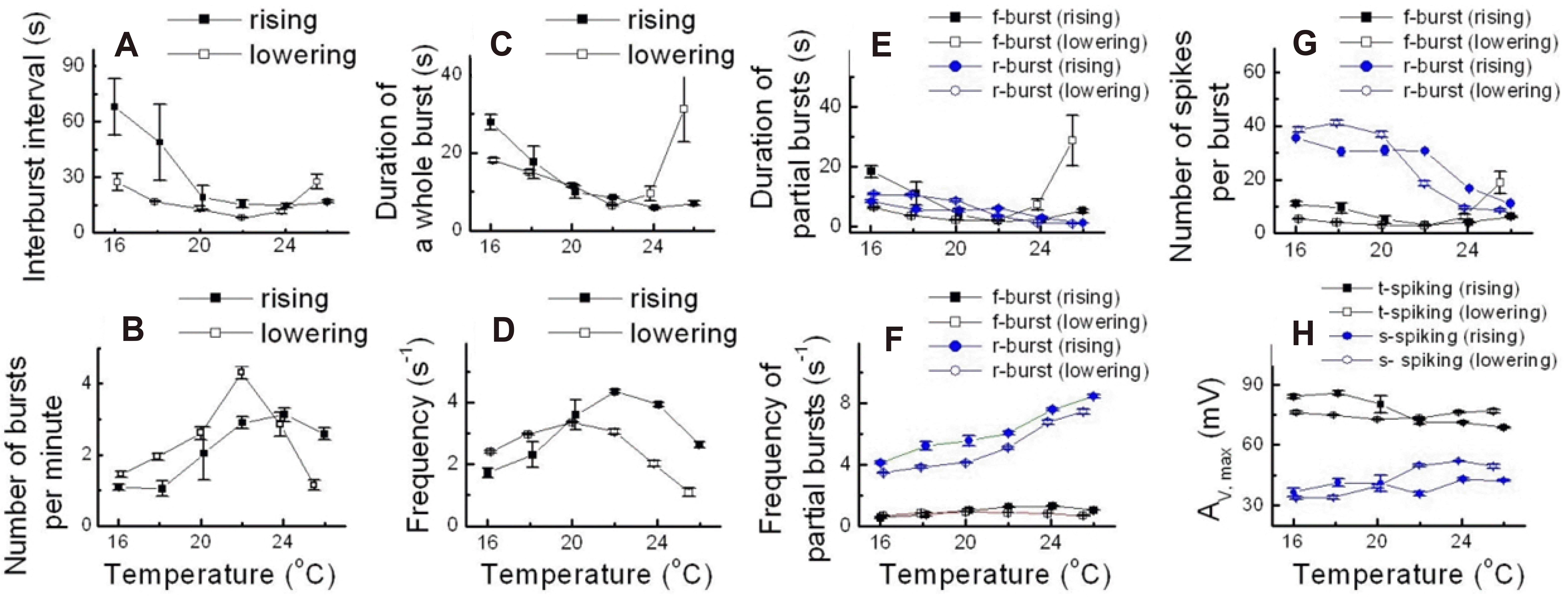
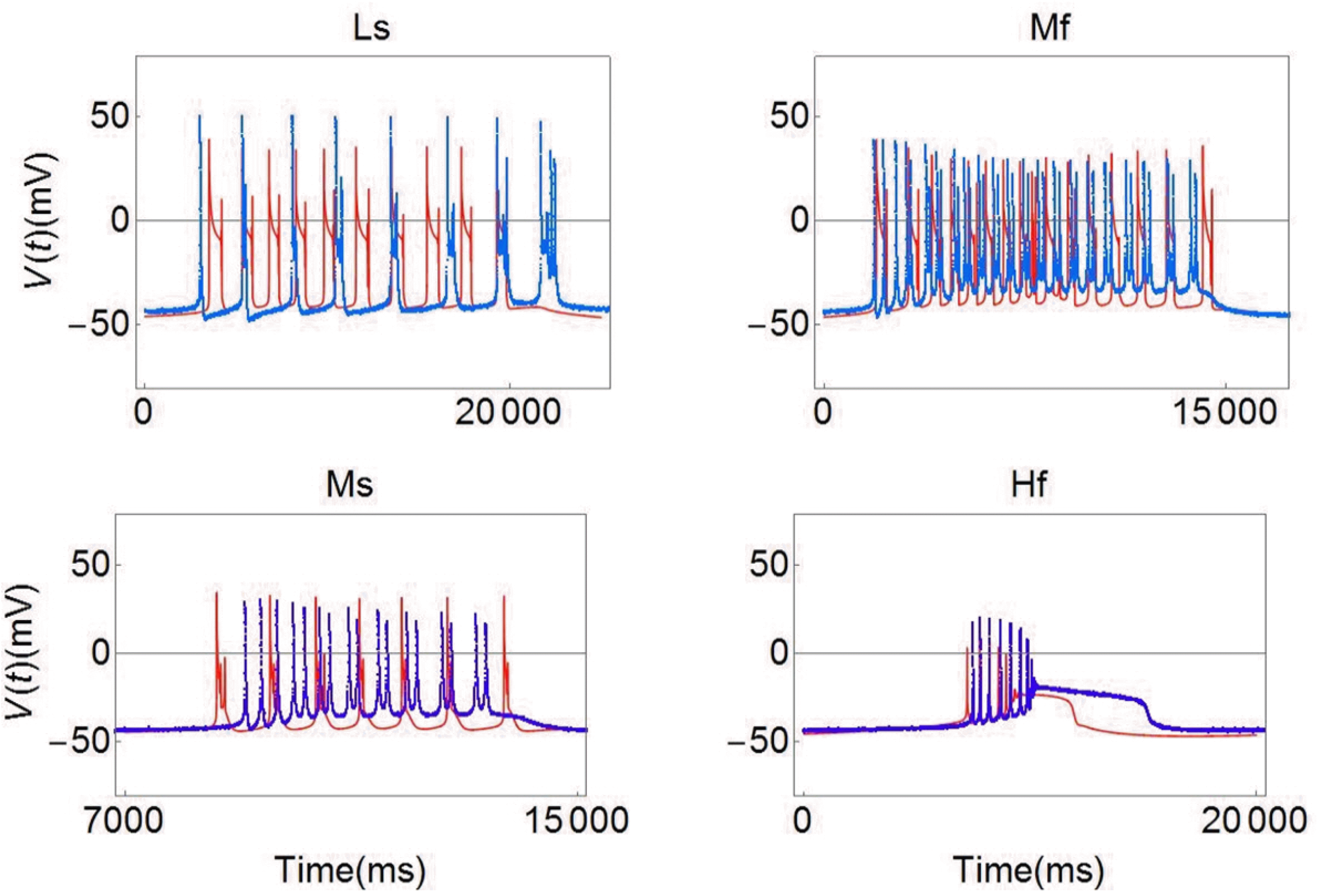
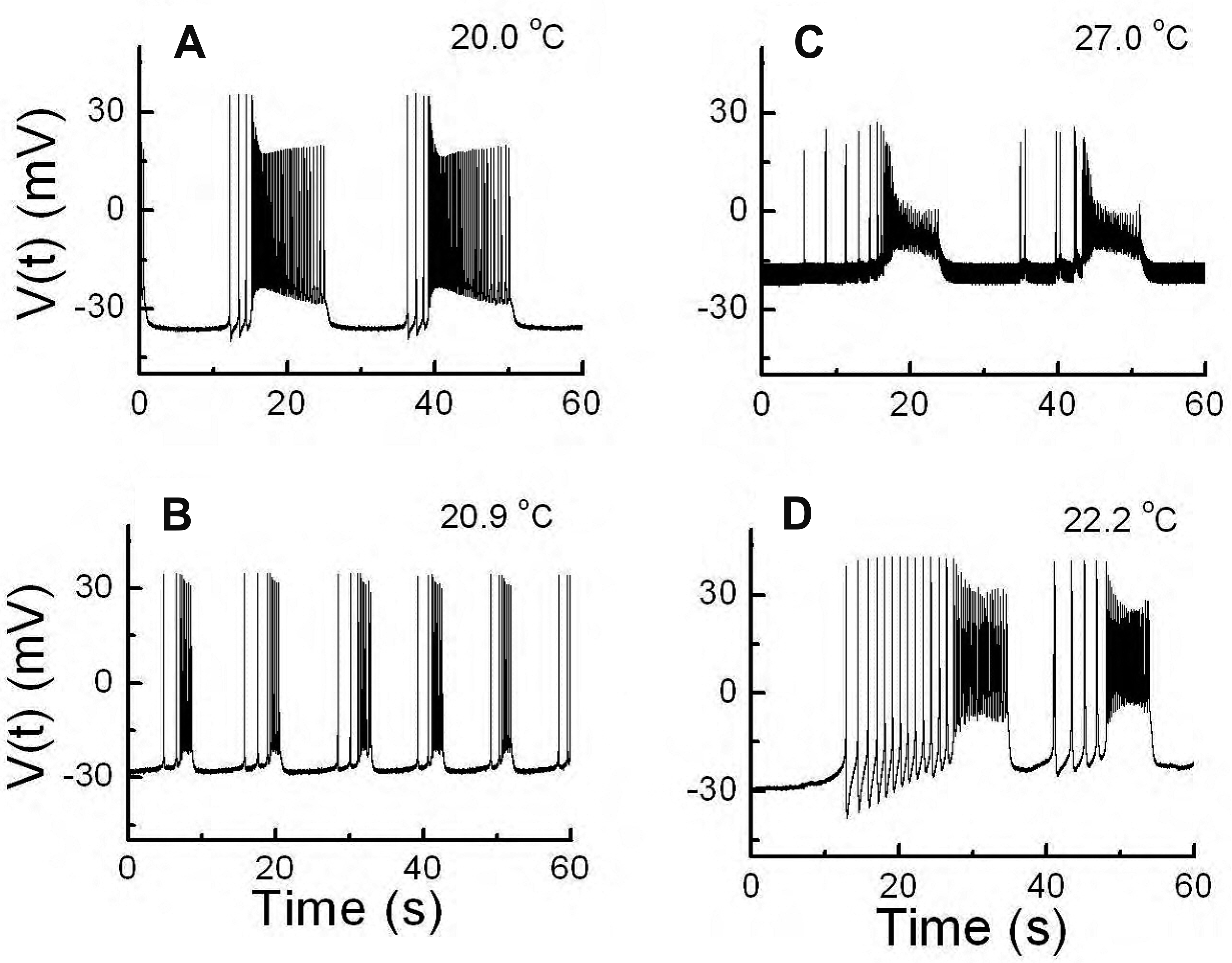
Overall description of experiments A to E
Previously we reported how the normal bursting pattern of R15 neurons in
Aplysia juliana changes with periodic temperature stimulation [
8]. In the present study, we sought to examine the bursting pattern of unspecified neurons in the abdominal ganglion of
Aplysia juliana with periodic stimulation of temperature change. For this purpose, we got the recording data from Experiments A to E. The bursting observed in Experiments A to D showed type 1 abnormal bursting patterns and the bursting of Experiment E exhibited type 2 abnormal bursting.
Table 1 describes the details of each experiment and presents two parts of the data obtained from five different experiments (Experiments A to E); data recorded at room temperature and data recorded during a period of temperature change. The data obtained from each experiment at room temperature revealed a stable AP before the temperature sweep. At room temperature, the average temperature ranges were from 15.2°C to 21.4°C, the average amplitude was from 42.7 mV to 70.9 mV, the maximum amplitude was from 55.9 mV to 76.7 mV, and the duration was from 14 min to 244 min.
A
max (mV) is defined as the difference between the maximum and minimum value of the membrane potential recorded for 1 min. Further information on computational analysis was published previously [
7-
9]. For temperature sweep data acquisition, the average temperature change was between 15.2°C and 27.8°C, the average recording duration was 1,024 min, the average number of temperature change cycles was 9, the average number of spikes was 20,269, and the average total recording time was 1,783 min. Microsoft visual C
++, Microcal Origin 6.0, and Mathematica 10.2 were used for data analysis, and results are presented as mean ± standard error (SE).
Specifications for experiment E (analysis of type 2 abnormal bursting)
During experiment E, 6,885 regular beatings were recorded at room temperature (~15°C) for 244 min, as shown in the 1st row in
Table 2. In the pre-cycle (from room temperature to the maximum temperature, then to the minimum temperature), 2,159 spikes were recorded. While periodically applying a sweep of temperature change to neurons in every 2 h cycle, the pattern of action potential firing, which depends on the temperature, changed regularly; each cycle is composed of an increase in temperature from about 13°C (temperature value in the silent state, each element in the 2nd column in
Table 2) to about 29°C (maximum temperature value, each element in the 7th column in
Table 2) followed by a decrease to about 13°C (temperature value in the silent state, each element in the 12th column in
Table 2). Briefly, the temperature was increased from about 13°C to about 29°C, then decreased to about 13°C. This cycle was continuously repeated for 44 cycles for 86 h.
Table 2
Specifications of experiment E
|
Cycle |
Silent |
Temperature when first spike was generated (°C) |
MNSPMRP |
Maximum temperature (°C) |
MNSPMLP |
Temperature when last spike was generated (°C) |
Silent |
TNS per cycle |
|
|
|
|
|
Temperature (°C) |
Duration (min) |
Temperature (°C) |
Number |
Temperature (°C) |
Number |
Duration (min) |
Temperature (°C) |
|
At RT |
Beating (duration = 244 min) |
6,885 |
|
Pre |
22.5 |
88 |
26.8 |
24.2 |
58 |
16.7 |
22 |
11.8 |
2,159 |
|
1st |
11.8 |
8 |
14.1 |
24.3 |
75 |
29.2 |
27.7 |
42 |
20.3 |
24 |
13.4 |
2,279 |
|
2nd |
13.4 |
5 |
13.5 |
24.8 |
56 |
29.0 |
26.2 |
32 |
18.9 |
21 |
13.7 |
1,836 |
|
3rd |
13.7 |
5 |
14.3 |
24.3 |
55 |
28.8 |
26.2 |
27 |
19.8 |
21 |
13.7 |
1,609 |
|
4th |
13.7 |
7 |
15.0 |
24.7 |
72 |
29.1 |
24.9 |
33 |
20.4 |
24 |
13.5 |
2,055 |
|
5th |
13.5 |
6 |
14.6 |
23.0 |
83 |
29.5 |
24.8 |
33 |
21.7 |
27 |
13.5 |
2,094 |
|
6th |
13.5 |
5 |
14.6 |
23.8 |
90 |
29.5 |
25.4 |
44 |
19.3 |
22 |
13.4 |
2,388 |
|
7th |
13.4 |
9 |
15.1 |
22.4 |
81 |
27.1 |
25.9 |
48 |
19.3 |
28 |
11.7 |
2,674 |
|
8th |
11.7 |
10 |
14.0 |
22.3 |
89 |
27.8 |
23.8 |
42 |
21.3 |
25 |
12.9 |
2,689 |
|
9th |
12.9 |
13 |
16.1 |
23.6 |
84 |
28.6 |
26.9 |
41 |
18.7 |
23 |
12.8 |
2,498 |
|
10th |
12.8 |
10 |
15.1 |
23.3 |
91 |
29.1 |
27.4 |
32 |
19.0 |
23 |
12.6 |
2,119 |
|
11th |
12.6 |
13 |
15.9 |
22.7 |
73 |
28.6 |
22.8 |
34 |
19.3 |
24 |
13.2 |
1,772 |
|
12th |
13.2 |
14 |
16.5 |
23.3 |
70 |
29.0 |
25.3 |
27 |
20.6 |
27 |
12.6 |
1,688 |
|
13th |
12.6 |
16 |
17.2 |
24.0 |
70 |
28.7 |
27.6 |
27 |
17.4 |
21 |
13.1 |
1,467 |
|
14th |
13.1 |
16 |
17.6 |
25.3 |
55 |
28.6 |
26.4 |
20 |
21.5 |
26 |
13.0 |
1,337 |
|
15th |
13.0 |
18 |
17.5 |
25.6 |
59 |
29.1 |
26.8 |
26 |
19.9 |
26 |
13.0 |
1,299 |
|
16th |
13.0 |
17 |
18.0 |
21.9 |
50 |
29.0 |
23.0 |
31 |
20.7 |
24 |
12.4 |
1,341 |
|
17th |
12.4 |
26 |
18.6 |
24.8 |
60 |
28.0 |
26.5 |
28 |
21.7 |
30 |
12.3 |
1,510 |
|
18th |
12.3 |
26 |
18.0 |
25.7 |
70 |
27.9 |
25.8 |
36 |
19.0 |
24 |
11.8 |
1,979 |
|
19th |
11.8 |
22 |
17.4 |
24.5 |
84 |
27.8 |
25.2 |
43 |
20.4 |
28 |
11.8 |
1,743 |
|
20th |
11.8 |
16 |
15.6 |
24.3 |
77 |
28.3 |
25.9 |
36 |
19.0 |
24 |
12.6 |
1,851 |
|
21th |
12.6 |
12 |
16.3 |
21.5 |
60 |
28.9 |
22.9 |
33 |
17.7 |
20 |
12.9 |
1,318 |
|
22th |
12.9 |
19 |
17.3 |
22.2 |
69 |
28.8 |
22.3 |
35 |
15.7 |
16 |
12.9 |
1,279 |
|
23th |
12.9 |
13 |
16.0 |
22.6 |
62 |
28.6 |
22.8 |
30 |
21.3 |
27 |
12.6 |
1,222 |
|
24th |
12.6 |
14 |
16.4 |
21.5 |
67 |
29.1 |
22.1 |
21 |
21.0 |
25 |
12.3 |
1,274 |
|
25th |
12.3 |
14 |
16.4 |
21.4 |
68 |
28.8 |
24.1 |
18 |
22.0 |
29 |
12.9 |
1,063 |
|
26th |
12.9 |
14 |
16.8 |
21.9 |
78 |
28.7 |
23.4 |
42 |
19.0 |
22 |
12.6 |
1,217 |
|
27th |
12.6 |
15 |
16.2 |
22.0 |
78 |
28.7 |
23.3 |
32 |
20.0 |
26 |
12.2 |
1,225 |
|
28th |
12.2 |
13 |
15.9 |
22.9 |
49 |
28.7 |
22.2 |
15 |
19.5 |
24 |
12.5 |
1,084 |
|
29th |
12.5 |
12 |
15.5 |
21.0 |
63 |
28.5 |
21.5 |
20 |
18.5 |
24 |
12.3 |
1,057 |
|
30th |
12.3 |
13 |
16.6 |
20.7 |
50 |
28.7 |
22.3 |
32 |
18.8 |
19 |
13.0 |
1,270 |
|
31th |
13.0 |
20 |
16.9 |
21.8 |
66 |
28.9 |
22.6 |
25 |
17.1 |
20 |
12.4 |
1,215 |
|
32th |
12.4 |
16 |
17.3 |
21.5 |
52 |
28.7 |
21.6 |
30 |
18.1 |
22 |
12.8 |
1,153 |
|
33th |
12.8 |
20 |
17.6 |
21.7 |
42 |
28.4 |
23.7 |
25 |
18.8 |
22 |
13.6 |
958 |
|
34th |
13.6 |
19 |
19.1 |
22.4 |
49 |
31.0 |
22.7 |
29 |
19.5 |
25 |
13.3 |
773 |
|
35th |
13.3 |
21 |
19.5 |
23.6 |
48 |
30.1 |
23.7 |
39 |
21.1 |
26 |
14.0 |
890 |
|
36th |
14.0 |
22 |
19.9 |
22.8 |
52 |
30.7 |
24.8 |
22 |
20.9 |
26 |
13.8 |
918 |
|
37th |
13.8 |
21 |
19.9 |
25.4 |
53 |
29.6 |
28.0 |
27 |
19.8 |
23 |
14.0 |
1,112 |
|
38th |
14.0 |
22 |
20.6 |
26.0 |
66 |
30.6 |
26.1 |
28 |
16.0 |
14 |
13.9 |
1,067 |
|
39th |
13.9 |
25 |
19.7 |
25.2 |
45 |
27.8 |
25.9 |
31 |
18.8 |
22 |
13.1 |
980 |
|
40th |
13.1 |
27 |
20.6 |
25.7 |
50 |
29.8 |
24.6 |
33 |
21.8 |
28 |
14.0 |
1,071 |
|
41th |
14.0 |
24 |
20.6 |
27.1 |
44 |
30.5 |
25.1 |
32 |
23.2 |
31 |
14.0 |
1,030 |
|
42th |
14.0 |
25 |
21.2 |
27.8 |
36 |
30.7 |
24.6 |
28 |
21.3 |
26 |
13.9 |
997 |
|
43th |
13.9 |
29 |
21.9 |
28.4 |
36 |
30.4 |
26.8 |
26 |
24.9 |
34 |
13.7 |
850 |
|
44th |
13.7 |
31 |
23.0 |
30.2 |
30 |
30.2 |
25.8 |
23 |
23.9 |
29 |
13.5 |
588 |
|
Average |
12.9 ± 0.1 |
16.4 ± 1.0 |
17.2 ± 0.3 |
23.7 ± 0.3 |
62.6 ± 2.3 |
29.0 ± 0.1 |
24.7 ± 1.8 |
30.8 ± 1.1 |
19.9 ± 0.2 |
24.3 ± 0.5 |
12.9 ± 0.1 |
1,450 ± 79 |

In the first three cycles, signals changed slightly after each cycle, and patterns did not show complete temperature dependence. After the 4th cycle, characteristic signals occurred repetitively at specific temperatures in each cycle. Therefore, although the total number of cycles was 44, we selected data from 34 of the 44 cycles and divided it into two halves (groups). To determine the temperature dependence and overall pattern change during the temperature change, we selected 34 cycles displaying stable activities (the 4th to the 37th cycle); cycles from the 4th to the 20th were assigned to the first group, and cycles from the 21th to the 37th were assigned to the second group. There were differences between signals from the first and second groups. In the first group signals appeared to be a mixture of two different patterns, and this was barely observed in the second group. Since these mixed signals became scarcer as the cycles proceeded, changes in patterns became more similar during each cycle. As summarized in
Table 2, for experiment E the average minimum temperature was 12.9°C ± 0.1°C. The first spike appeared at an average temperature of 17.2°C ± 0.3°C after an average of 16.4 ± 1.0 min during the silent phase. An average of 62.6 ± 2.3 maximum numbers of spikes per min appeared at an average temperature of 23.7°C ± 3°C during the rising phase. An average of 29.0°C ± 0.1°C was the maximum temperature during the temperature change cycle. An average of 30.8 ± 1.1 maximum number of spikes per min appeared at an average of 24.7°C ± 1.8°C in the lowering phase. Below an average of 19.9°C ± 0.2°C, no further spiking appeared. In a last silent phase of the cycle, the average duration was 24.3 ± 0.5 min and the average minimum temperature was 12.9°C ± 0.1°C.
Modified Plant model for simulation of type 2 abnormal bursting
To simulate the temperature-dependent bursting patterns of neurons in
Aplysia, we modified the Plant model [
12,
13] with temperature-dependent scaling factors [
7,
8,
14]. The Plant model was used previously to analyze fast and slow processes during parabolic bursting [
15]. In our present study, the components of the modified Plant model include a fast sodium current I
Na, a fast potassium current I
K, a slow inward calcium current I
Ca, calcium-activated potassium current I
K(Ca), and leak current, I
Cl.
where
and
where V represents the membrane potential, and VNa, VCa, VK, and VCl are the reversal potentials for the Na+, Ca2+, K+, and Cl– currents, respectively. _gNa, _gCa, _gK, and _gCl are the maximal conductances for the respective currents, and _gK(Ca) is the maximal conductance for the calcium-activated potassium current. The voltage-dependent activation and inactivation variables are expressed as m and h, respectively. The activation variable for the potassium channels is n. The slow activating conductance for the calcium current is expressed as χ.
Ca, which denotes the intracellular free calcium concentration, is treated as a parameter. The maximal relaxation time constants of h and n are represented by
_τh and
_τn, respectively, and ρ
–1 is an estimation of the time-constant of the Ca equation. The temperature-dependent scaling factor ρ(T) is defined as
ρ(T)≡1.3T-T010°C, and is also defined as
φ(T)≡3T-T010°C [
7,
8]. The steady-state values of activation (inactivation) variables –m
∞, χ
∞, and n
∞(h
∞) are functions of voltage. τ
h, τ
χ, and τ
n are relaxation time constants. Constant values for defining equations for steady-state values of activation (inactivation) variables and relaxation constants are represented by aa, bb, cc, dd, c
1, c
2, m
1, m
2, m
3, h
1, h
2, c
5, c
6, c
7, c
8, etc.
Glossary for equations
A, action potential amplitude
Aave, averaged action potential amplitude
Amax, maximum action potential amplitude
Ca, slow change in intracellular free calcium concentration
ICa, slow inward calcium current
IK, fast potassium current
IK(Ca), calcium-activated potassium current
ICl, leak current
INa, fast sodium current
T0, reference temperature (= 21.6°C)
V, membrane potential
VCa, reversal potential for calcium current
VK, reversal potential for potassium current
VCl, reversal potential for leak current
VNa, reversal potential for sodium current
Vmin, membrane potential at the negative peak
Cm, membrane capacitance
_gCa, maximal conductance for calcium ion current
_gK, maximal conductance for potassium ion current
_gK(Ca), maximal conductance for calcium activated potassium ion current
_gCl, maximal conductance for leak current
_gNa, maximal conductance for sodium ion current
h, voltage-dependent inactivation variable for sodium channel
m, voltage-dependent activation variable for sodium channel
n, activation variable for potassium channel
Kp, dissociation constant
Kc, constant values involved in the calcium ion concentration
aa, bb, cc, dd, a, b, c1, c2, m1, m2, m3, h1, h2, c5, c6, c7, c8, constant values involved in defining an equation for steady-state values of activation (inactivation) variables and relaxation constants
_τh, maximal relaxation time constant of h
_τn, maximal relaxation time constant of n
τh, τχ, τn, relaxation constant of h, χ, and n respectively
χ, slowly activating conductance for calcium current
ρ–1, estimation for the time-constant of the Ca-equation
ρ(T), temperature-dependent scaling factor; ρ(T)≡1.3T-T010°C
φ(T), temperature-dependent scaling factor; φ(T)≡3T-T010°C




 PDF
PDF Citation
Citation Print
Print



 XML Download
XML Download