Go to : 
INTRODUCTION
Creatinine is a breakdown product of creatine phosphate, particularly in muscle, and it is usually produced at a fairly constant rate by the muscles. This product is freely filtered and excreted into the urine by the kidney. In clinical settings, serum creatinine (Scr) measurements have been most commonly used to evaluate kidney function. The glomerular filtration rate (GFR) is defined as the flow rate of the filtered fluid through the kidney, and many equations have been developed to calculate estimated GFR (eGFR) based on Scr, including the modification of diet in renal disease (MDRD), the chronic kidney disease-epidemiology collaboration (CKD-EPI), Cockcroft–Gault, and Nankivell equations [1-4]. However, the measurement of Scr is prone to different types of error, and the interpretation of renal excretory function based on this measurement can be affected by various sources of interference, thereby making the measurements imprecise [5]. Although the Scr level is high during the early kidney transplantation period, the true renal excretory function of the graft is not low. Actual renal function is not increasing in proportion to the decline in the Scr level. The renal function might be the same regardless of the Scr level in transplantation settings. Therefore, a novel approach is needed when using Scr equations in the context of transplantation.
Some degree of ischemia and reperfusion injuries to the kidney graft are inevitable during transplant surgery. Delayed graft function (DGF) is generally defined as a transient discrepancy between the functional capacity of the transplanted kidney and fulfilment of the physiological needs of the recipient, as manifested by oliguria, lack of Scr decrease, or transient dependency on dialysis. It is still debated whether DGF, as the principal manifestation of initial ischemia/reperfusion injury, alone affects the ultimate behavior of the graft [6-8]. During the reperfusion period after the transplant, the kidney graft should exhibit functional recovery from ischemia/re-perfusion injury. Therefore, the excretory function might change over time after kidney transplantation. The patterns of the changes in renal function after transplantation remain unknown. We attempted to establish new-model equations based on the fact that the change in the creatinine concentration equals the input subtracted by the output of creatinine. These equations could be more applicable in the post-transplant period.
Go to : 
METHODS
All patients provided written informed consent and the Institutional Review Board of Ajou University Hospital approved this study (IRB No. AJIRB-MED-MDB-18-367).
Study Population
Total six hundred and twenty-three kidney allotransplantations were performed at Ajou University Hospital from January 2008 to June 2018. No selection procedures were applied. This was a retrospective and observational study.
Surgical Procedure of Kidney Transplantation
The standard surgical techniques of revascularization and urinary tract reconstruction were used for all transplantations included in this study. Vascular clamps were placed at the recipient’s iliac artery and vein to control the blood flow during vascular anastomosis. Immediately after anastomosis of the graft renal vein and artery to the recipient’s iliac vein and artery, the vascular clamps were released to restore blood flow to the kidney graft. The time of re-perfusion is defined as the time at which the vascular clamps were released. The ureter was implanted in the bladder using extravesical Lich-Gregoir ureteroneocystostomy [9,10].
Scr Measurement
Scr was measured using an automated assay on the Cobas 8000 C702 system (Roche Diagnostics, Basel, Switzerland).
Immunosuppression
The immunosuppression regimen consisted of cyclosporine (n=124, 19.9%) or tacrolimus (n=499, 80.1%), corticosteroids, and enteric coated mycophenolate sodium or mycophenolate mofetil. The calcineurin inhibitor cyclosporine or tacrolimus was administered orally at a dose of 10 mg/kg/day or 0.2 mg/kg/day, respectively, starting one or two days before the transplantation. Within a month after transplantation, the dose of the drug was individually adjusted with a goal trough blood level between 200 and 250 ng/mL for cyclosporine or between 5 and 10 ng/mL for tacrolimus. Here, the nephrotoxicity of the calcineurin inhibitor was clinically defined as reversible graft dysfunction with evidence of a substantially high concentration of the drug in the blood.
Mathematical Model Equations for Unchanged Renal Function
With respect to creatinine output, blood creatinine is cleared mostly by the kidney. However, extra-renal clearance, most likely by intestinal bacteria, could be relevant in cases of severe chronic renal disease [11]. Regardless of these physiological features that limit the use of Scr to calculate renal function, the following basic equation involving the input, output, and blood concentration of creatinine can be used: vdydt=m–vcy, where y=Scr (mg/dL), v=volume in which creatinine is evenly distributed (dL), m=rate of creatinine input (mg/hr), c=volumetric proportion of creatinine excretion per unit time (/hr), and dydt=change in the Scr concentration per unit time (mg/dL/hr). The parameter c is considered a constant (unchanged over time) if the renal excretory function is unchanged. The derivation of equations from this basic differential equation should consider various scenarios. First, the rate of creatinine input is greater than the creatinine output which is usually observed in transplant patients, and this can be expressed as
where k1(hr) is constant of integration. Second, the rate of creatinine input is the equal to the rate of creatinine output, and this can be expressed as
Third, the kidney function is almost zero (c=0), and this can be expressed as
where k3 is constant of integration (mg/dL).
Mathematical Model Equations for Improving Renal Function
An equation describing kidney function recovery should have the following properties: the equation should be continuous and integrable, always yield a value equal to or higher than 0, and provide incremental values until the asymptote. The logistic equation, which represents the time-varying carrying capacity, could be used in the following first-order linear differential equation. As logistic equations are commonly used to model population growth, this type of equation could also be used to model the functional recovery pattern of a kidney graft after transplantation. The basic concept underlying the modified logistic equation is dCdt=rC(1-cr), where r=rate of functional recovery and maximal functional capacity and C(t)=volumetric proportion of creatinine excretion per unit time (/hr) depending on the time variable. As a kidney with a greater functional reserve (maximal functional capacity) can more quickly recover its function (rate of functional recovery) after transplantation, it can be hypothesized that the growth rate and the carrying capacity in the original logistic equation are equal in the modified logistic equation. The following new generalized and deterministic equations for renal function and Scr can be derived
where a is a unitless constant and k5 is the constant of integration (hr). Finally, the mathematical association between Scr (y) and renal function (C) can be expressed as
Curve Fitting of the Models
The time intervals from re-perfusion during the surgical procedure to blood collection for measuring Scr until 30 days post-transplantation were calculated. The recipient’s Scr was measured every four hours on the first day and postoperatively on a daily basis. The time intervals and the laboratory results for the Scr measurements for each patient were inputted into Excel 2016 (Microsoft, Redmond, WA, USA). A total of 14,360 values were predicted using the model equations, and these were compared to measured Scr levels. For each patient, the values of the constants m/v, c, and k1 in equation 1 and r, a, k5, and m/v in equation 5 were individually obtained using the Excel 2016 “solver” function. To use the solver function, the objective cell was set to the minimal value of the sum of the squares of (model value-measured value), and the decision variables were the constants of equations 1 and 5. When the Scr of a recipient reached the baseline level, the recipient’s 24-hour urine was collected to determine the amount of excreted creatinine. This information was used to obtain the value of the constant “m” in equations 1 and 5.
Statistical Analysis
The values calculated using the model equations and the measured values were included in a linear regression analysis to determine the R2 (R square, coefficient of determination) and F-test values. A good curve fit with the measured Scr was strictly defined based on an R2 value greater than 0.95 for each equation. The unstandardized beta-coefficients for the constant and the coefficient were obtained using the P-value. The Durbin–Watson test values to measure auto-correlation in residuals from regression analysis were also obtained using IBM SPSS ver. 20 (IBM Corp., Armonk, NY, USA). Autocorrelation is the similarity of a time series over successive time intervals. The Durbin–Watson test reports a test statistic with a value from 0 to 4, where 2 is no autocorrelation.
Go to : 
RESULTS
Demographic Characteristics
All 623 patients who underwent kidney transplantation from January 2008 to June 2018 at a single institute were included to validate the mathematical equations for Scr, and 14,360 laboratory results for Scr from the time of transplantation (the time of re-perfusion) to 30 days post-transplantation were analyzed. The mean±standard deviation of the number of Scr measurements obtained from a patient at various time points post-transplantation is 23.05±4.07. Two hundred and sixty-six patients received a kidney from live donors, and three hundred and fifty-seven patients received a kidney from the deceased donors. Means±standard deviations of recipient age and donor age were 46.8±10.4 and 44.6±14.5 years, respectively; 256 recipients and 246 donors were women. Means±standard deviations of recipient weight (kg) and donor weight (kg) were 61.8±11.34 and 65.7±12.9, and those of recipient height (cm) and donor height (cm) were 164.7±8.7 and 166.0±9.0, respectively.
Validation of the Model (Equations 5 and 1)
An overall linear regression analysis yielded an R2 value for equation 5 of 0.972 (Fig. 1A), and the corresponding value for equation 1 was 0.925 (Fig. 1B). The F-test was used to determine whether the model is a good fit to the data, and the results yielded values of 504,146.461 (P<0.001) for equation 5 and 176,290.156 (P<0.001) for equation 1. The unstandardized beta-coefficient of equation 5 shows that the constant is –0.010 and the coefficient is 1.002 (P<0.001), and the unstandardized beta-coefficient of equation 1 shows that the constant is –0.010 and the coefficient is 1.003 (P<0.001). The Durbin–Watson test values to measure auto-correlation in residuals from regression analysis yielded 1.962 for equation 5 and 1.856 for equation 1. Equation 5 for improving renal function is more generalized and more applicable than equation 1 for unchanged renal function (Fig. 1C).
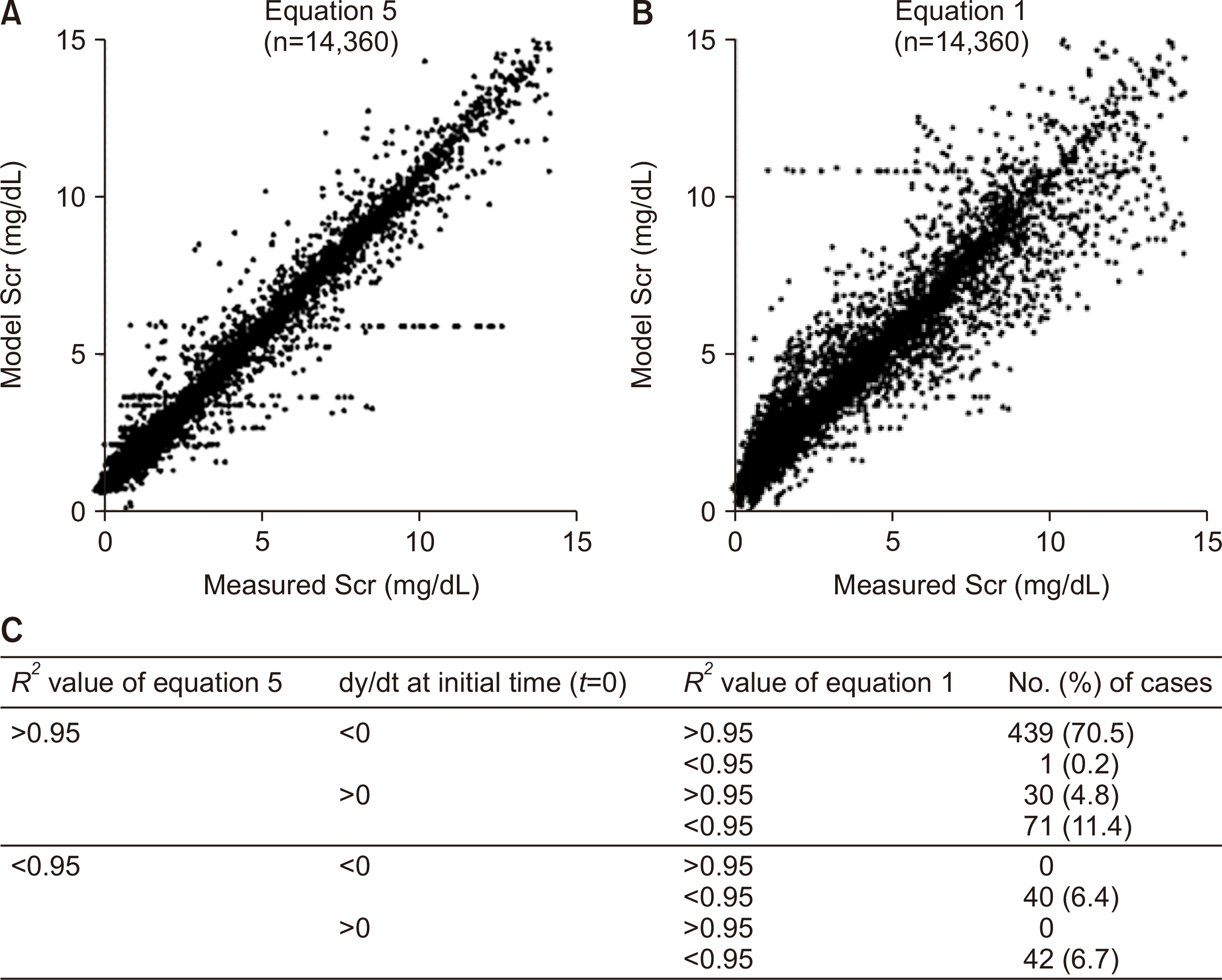 | Fig. 1Validation of model equations for serum creatinine (Scr) in total population. (A) Distribution of measured Scr values for the total population (n=623) and values obtained using equation 5 m(ertr+at+k5)v(ert+a). The R2 value is 0.972, and F-test value is 504,146.461 (P<0.001). (B) Distribution of measured
Scr values for the total population (n=623) and values obtained using equation 1 mvc{1+e-c(t+k1)}. The R2 value is 0.925, and F-test value is 176,290.156 (P<0.001). (C) Fitness characteristics of the model equations for the total population (n=623). For each equation, good curve fit to the measured Scr values is defined as an adjusted R2 value greater than 0.95. Among the 541 (86.9%) cases that showed good fit with equation 5, the initial dydt values of 101 cases (18.7%) are greater than 0. Among the 101 cases with initial dydt>0, 71 cases (70.3%) showed poor fit with equation 1. None of the cases that showed poor fit with equation 5 showed good fit with equation 1. Equation 5 for improving renal function is more generalized and more applicable than equation 1 for stable renal function.
|
An individual linear regression analysis of 623 patients showed that R2 values greater than 0.95 were obtained for equation 5 in 86.8% (541 cases) of the patients and equation 1 in 75.3% (469 cases) of the patients. The cases of poor fit between the values obtained with equation 5 and the measured values of Scr (R2<0.95) were clinically reviewed to determine the causes of this discrepancy, and the results revealed 26 cases of post-transplant dialysis, 15 episodes of rejection, 11 postoperative complications, 24 calcineurin inhibitor nephrotoxicities, 1 systemic and local infection, and 5 transient graft dysfunctions due to an undetermined cause.
Classification of the Functional Recovery Pattern Based on Equations 4 and 5
Using equation 4, the initial renal function immediately after re-perfusion following transplant surgery can be calculated as C(0)=r(1+a). The time at which a transplanted kidney recovers 99% of its functional capacity (r) is t=In(99a)r, and in general terms, the time at which the kidney recovers x% of its functional capacity (r) is t=1rInax(100-x). The proportion
of pre-transplant renal injury to expected full function of the graft can be calculated as r-C(0)r=a1+a. Five types of
functional recovery patterns were classified based on the severity of the pre-transplant injury and the speed of the functional recovery of the kidney graft post-transplantation (Fig. 2).
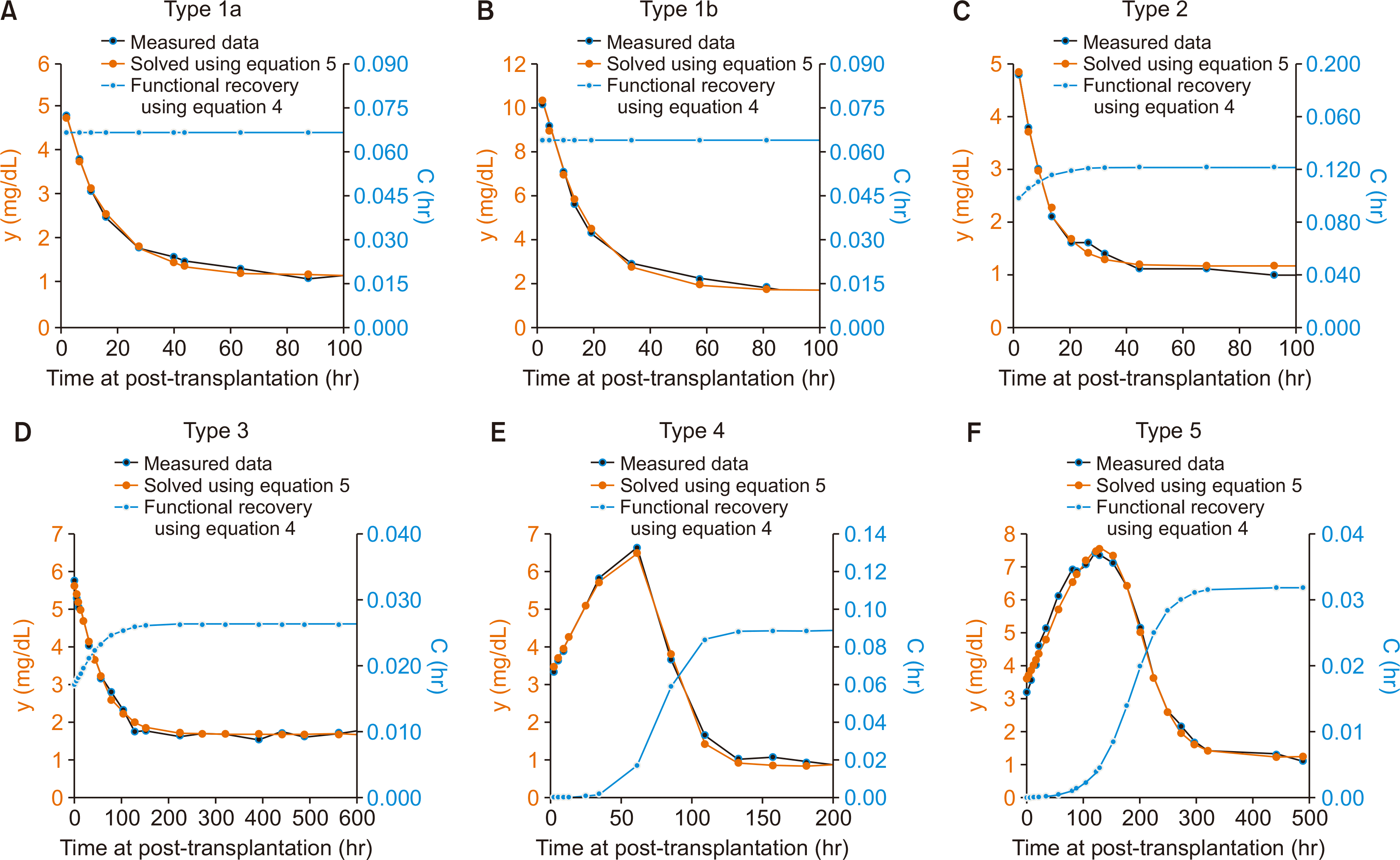 | Fig. 2Classification of the severity of pretransplant renal injury and recovery time at post-transplantation. (A) Example of type 1a. r=0.066472 (/hr), a=0.000000, k5=51.572055 (hr), m/v=0.077876 (mg/dL/hr). No pretransplant injury: 129 cases (23.8%). The constant “a” in equation 5 is nearly 0, and the constant “c” in equation 4 is equal to constant “r” in equation 5, which clinically suggests that the kidney graft reached full function immediately after reperfusion, and no further recovery of renal function was achieved after transplantation. (B) Example of type 1b. r=0.064122 (/hr), a=0.001416, k5=91.153870 (hr), m/v=0.106519 (mg/dL/hr). Minimal (1%) pretransplant injury: 29 cases (5.4%). The proportion of pre-transplant renal injury to expected full function of the graft, (r-C(0)r=a1+a), is less than 1%. (C) Example of type 2. r=0.121604 (/hr), a=0.293297, k5=41.148330 (hr), m/v=0.140837 (mg/dL/hr). Moderate (1%–50%) pretransplant injury and rapid functional recovery: 88 cases (16.3%). 0.01<(r-C(0)r=a1+a)≤0.5, and the recovery time required to reach 99% of the expected full function (functional capacity), t=In(99a)r based on equation 4, is less than 36 hours. (D) Example of type 3. r=0.026282 (/hr), a=0.591045, k5=170.169239 (hr), m/v=0.043779 (mg/dL/hr). Moderate (1%–50%) pretransplant injury and slow functional recovery: 90 cases (16.6%). 0.01<r-C(0)r=a1+a≤0.5, t=In(99a)r≥36 hours. (E) Example of type 4. r=0.088510 (/hr), a=983.131123, k5=43,805.651890 (hr), m/v=0.073571 (mg/dL/hr). Severe (>50%) pretransplant injury and rapid functional recovery: 103 cases (19.0%). r-C(0)r=a1+a> 0.5, t=In(99a)r<144 hours (6 days). (F) Example of type 5. r=0.031957 (/hr), a=354.134151, k5=32,054.956071 (hr), m/v=0.039461 (mg/dL/hr). Severe (>50%) pretransplant injury slow functional recovery: 102 cases (18.9%). r-C(0)r=a1+a>0.5, t=In(99a)r≥144 hours (6 days). |
Distribution of the Parameters, Pre-transplant Injury, and 99% Recovery Time
The median interquartile range of the constants r (/hr), a, k (hr), and m/v (mg/dL/hr) in the Scr equation were 0.074 (0.039–0.120), 0.533 (0.000–2.141), 118.525 (61.936–313.240), and 0.090 (0.055–0.134), respectively. Those of the proportion of the amount of kidney injury to maximal functional reserve (%) and the time of 99% of functional recovery (hr) were 34.79 (0.00–68.16) and 48.505 (27.107–152.751), respectively. Also, those values for each type of function recovery pattern after transplantation are displayed in Table 1.
Table 1
Distribution of the parameters, pre-transplant injury, and 99% recovery time
Comparison between Commonly Used eGFR Formulas and Creatinine Clearance Calculated Using the Model
Most of the eGFR formulas are mathematically applicable only if dydt=0. For example, for the type 1 functional recovery pattern (Fig. 3), even though the renal function does not change continuously after transplantation, the Scr level decreases to a certain asymptote (baseline), which results in an increase in eGFRs. The eGFRs calculated using Scr are not mathematically applicable until the Scr reaches a certain value (i.e., when dydt approaches 0, which reflects an equilibrium state in which the creatinine input rate equals the creatinine output rate). Although renal graft function continuously increases in the type 4 and 5 cases, the Scr level can initially increase because the creatinine output is less than the creatinine input. Until the Scr reaches a plateau or a certain level (i.e., when dydt approaches 0), the eGFR equations are not mathematically applicable. The differences between eGFRs and creatinine clearance (eGFR-CCr) decrease as dydt approaches 0 (Fig. 4). The difference between eGFRs and CCr (eGFR-CCr) is greater and widely distributed as dydt is far from 0. If dydt<0, the eGFR equations provide an underestimation; in contrast, the eGFR equations overestimate the results if dydt>0.
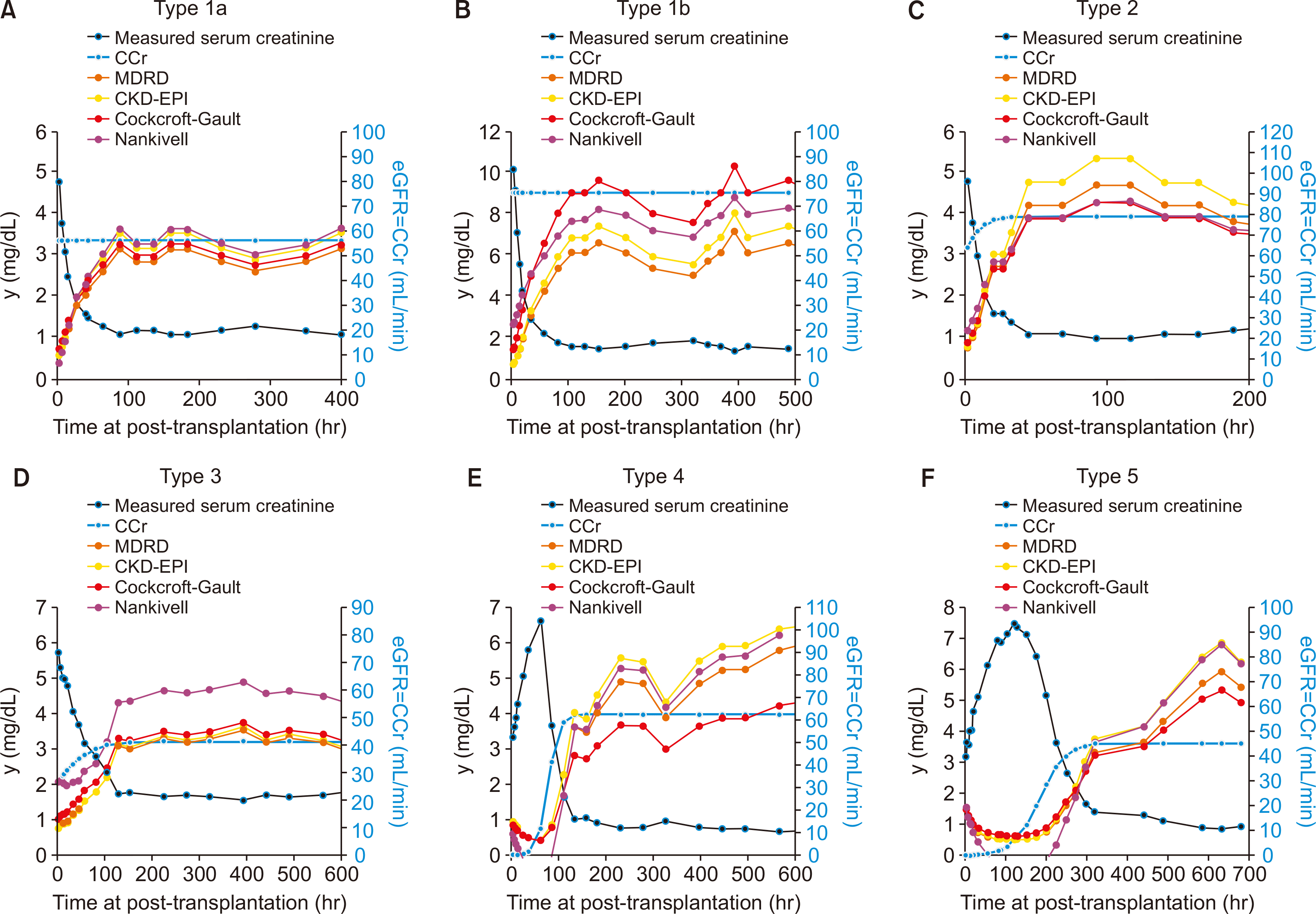 | Fig. 3Comparison of estimated glomerular filtration rates (eGFRs) and modeled creatinine clearance (CCr) for the example case of different types. (A) Comparison of eGFRs and modeled CCr for type 1a case. r=0.066472 (/hr), a=0.000000. (B) Comparison of eGFRs and modeled CCr for type 1b case. r=0.064122 (/hr), a=0.001416. (C) Comparison of eGFRs and modeled CCr for type 2 case. r=0.121604 (/hr), a=0.293297. (D) Comparison of eGFRs and modeled CCr for type 3 case. r=0.026282 (/hr), a=0.591045. (E) Comparison of eGFRs and modeled CCr for type 4 case. r=0.088510 (/hr), a=983.131123. (F) Comparison of eGFRs and modeled CCr for type 5 case. r=0.031957 (/hr), a=354.134151. MDRD, modification of diet in renal disease; CKD-EPI, chronic kidney disease-epidemiology collaboration. |
 | Fig. 4Distribution of estimated glomerular filtration rate (eGFR)- creatinine clearance (CCr) as a function of dydt. (A) Scatter plot of modification of diet in renal disease (MDRD) eGFR-modeled CCr as a function of dydt. (B) Scatter plot of chronic kidney disease-epidemiology collaboration (CKD-EPI) eGFR-modeled CCr as a function of dydt. (C) Scatter plot of Cockcroft-Gault eGFR-modeled CCr as a function of dydt. (D) Scatter plot of Nankivell eGFR-modeled CCr as a function of dydt. |
Scr levels (1,508) were measured within the narrow range of –0.000000002<dydt<0.000000002, and the corresponding eGFRs were calculated and compared to the CCr. Pearson’s correlation coefficients for the correlations of the MDRD, CKD-EPI, Cockcroft-Gault, and Nankivell eGFRs with the CCr were 0.446 (P<0.001), 0.459 (P<0.001), 0.651 (P<0.001), and 0.599 (P<0.001), respectively. Linear regression analysis showed that R2 values for the MDRD eGFR were 0.199, and those for the CKD-EPI, Cockcroft-Gault and Nankivell eGFRs were 0.211, 0.423, and 0.359, respectively. The F-test yielded values of 373.735 (P<0.001) for the MDRD eGFR, 402.860 (P<0.001) for the CKD-EPI eGFR, 1,105.812 (P<0.001) for the Cockcroft-Gault eGFR, and 842.871 (P<0.001) for the Nankivell eGFR (Fig. 5).
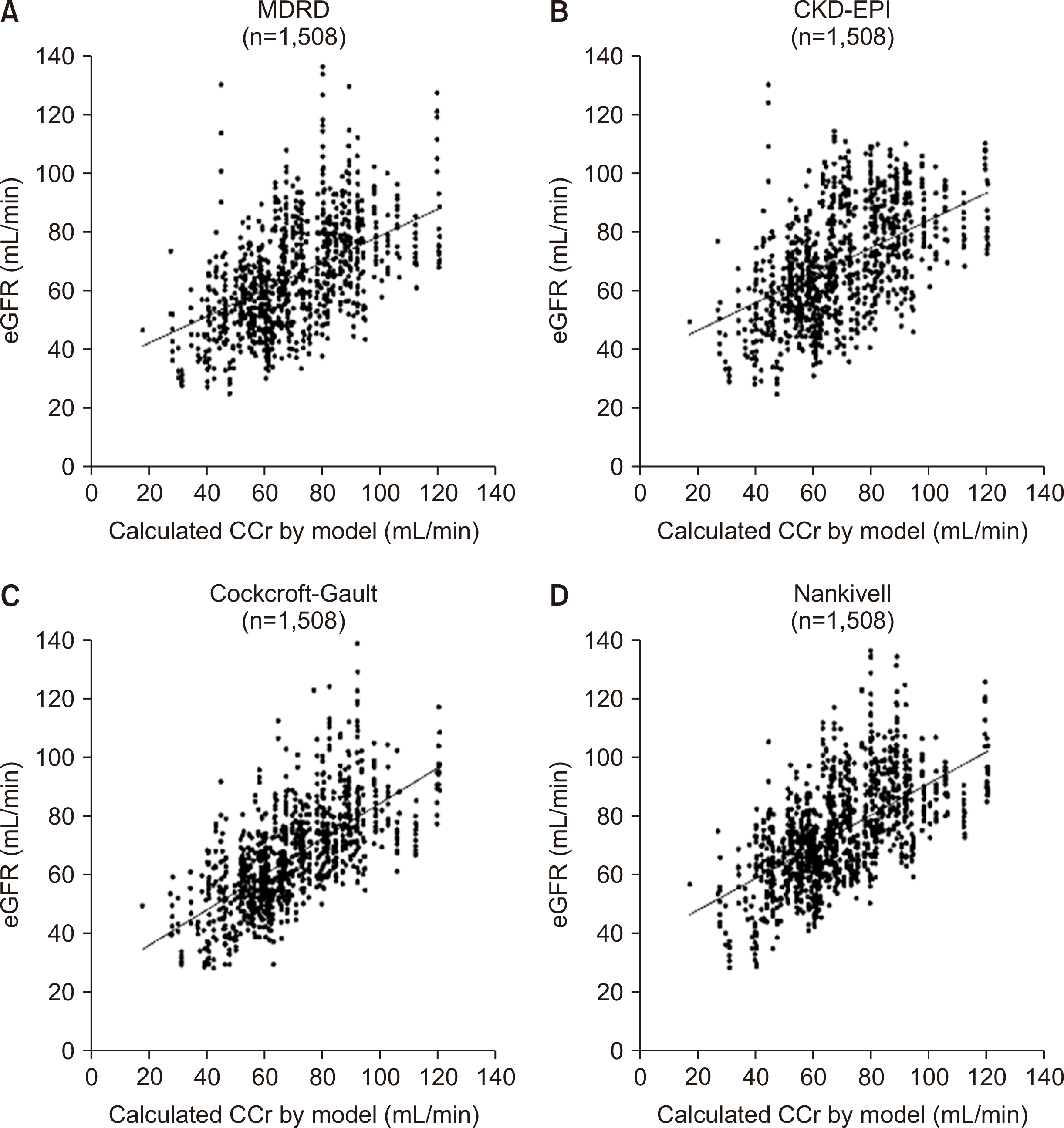 | Fig. 5Correlation between estimated glomerular filtration rate (eGFR) and modeled creatinine clearance (CCr) at dydt≒0. (A) Scatter plot of modification of diet in renal disease (MDRD) eGFR as a function of the CCr obtained with the model at –0.000000002<dydt<0.000000002. (B) Scatterplot of chronic kidney disease-epidemiology collaboration (CKD-EPI) eGFR as a function of the CCr obtained with the model at –0.000000002<dydt<0.000000002. (C) Scatterplot of Cockcroft-Gault eGFR as a function of the CCr obtained with the model at –0.000000002<dydt<0.000000002. (D) Scatterplot of Nankivell eGFR as a function of the CCr obtained with the model at –0.000000002<dydt<0.000000002. |
Go to : 
DISCUSSION
Scr measurement has been the most commonly used laboratory test for estimating the excretory function of the kidney. The mathematical or statistical association between Scr and renal function is crucial. The Kidney Disease Improving Global Outcomes statement proposes that creatinine-based eGFR equations should be used to evaluate the renal function in the everyday management of renal transplant recipients [12]. Most of the commonly used eGFR equations have been developed via statistical analysis of patients with chronic kidney disease. However, kidney transplant recipients comprised only 4% of the cohort used to derive the CKD-EPI eGFR equation. Several studies on kidney transplantation have reviewed the efficiency of the MDRD, Cockcroft-Gault and Nankivell equations, and the results have shown significant heterogeneity between studies and indicated that the equations show low precision and, consequently, limited accuracy [13]. Scr-based eGFR equations have never been demonstrated to improve the clinical recognition of changes in transplant function [14]. The basic assumption of the eGFR equations is that Scr does not change or only changes at a slow rate over time (dydt≒0). However, the Scr level usually changes very rapidly as the kidney graft exhibits functional recovery beginning immediately after kidney transplantation. The basic assumptions of the new equation should consider that Scr can change (dydt≠0) over time and that the renal excretory function can also change (dCdt≠0) over time. The pattern of the change in renal function should represent the functional recovery of a transplanted kidney from pre-transplant or ischemic injuries (dCdt≥0). Equation 5 y=m(ertr+at+k5)v(ert+a) was demonstrated to explain the changes in the measured Scr level over time in recipients with an uneventful post-transplant course. If equation 5 explains the measured Scr, equation 4 C(t)=rertert+a is useful for calculating the renal excretory function at a certain time. The degree of kidney injury before or during transplantation and the rate at which it recovers function after transplantation can be calculated using equation 4, and these calculated values are essential for research on DGF. It is difficult to find a simple definition of DGF due to the complexity of DGF pathophysiology, which explains why more than ten different definitions currently exist [8,15]. The most common definition of DGF is based on the post-transplant dialysis requirements (at least one dialysis session during the first week after transplantation). Although useful for data reporting, this definition suffers from many pitfalls, including clinically dependent decisions, dialysis requiring potassium or fluid overload, metabolic acidosis, and uremic symptoms, which might lead to misclassification or large variations in DGF rates that are observed in multicenter trials [16]. For more accurate data reporting, the mathematically derived equation 4 of the model can be used as the definition for DGF.
Among the mathematical models that the authors described, the model equation for improving renal function was regarded as the most complex and important mathematical model in this study. The assumption of a renal recovery pattern is a key hypothesis of this study because the functional recovery of transplanted kidney is not justified as a simple equation. As mentioned in the methods section, the authors assumed that the functional recovery of transplanted kidney should be continuous, integrable, and yield a value equal to or higher than 0. Furthermore, we assumed that the functional recovery of transplanted kidney should change over time and converge to zero when renal excretory function reaches the maximal functional capacity. As a result, it was appropriate that the logistic equation that explained a common model of population growth was the most suitable equation for our assumptions. Of course, there was a difference between the basic logistic equation and our equation that the rate of functional recovery and the maximal functional capacity were defined as an equal variable. The authors assumed that a graft kidney with a greater functional capacity would recover graft function more quickly. One of the major pieces of evidence supporting this assumption is that the grafts with different maximal functional capacity recover their function within a very short time after transplantation and reach the maximal functional capacity in the case of no post-transplant kidney injury. Therefore, the rate of recovery of the graft with the greater functional capacity should be relatively faster than the rate of other grafts. Further, theoretically, there is no significant mathematical error in setting two variables as an equal value in this equation.
Here, we assumed that there was little or no change in volume of creatinine distribution within the study period. We argue that perioperative volume resuscitation and fluid shifts can affect the volume of distribution in kidney transplant recipients. When the authors defined ‘v’ (volume in which creatinine is evenly distributed) in vdydt=m–vcy, ‘v’ was not a measured value but a value calculated by other variables. Additionally, creatinine is produced mainly by the body muscles, and each kidney transplant recipient has a different muscle burden, meaning that creatinine production may not be proportional to body weight. For example, the calculated ‘v’ of recipients who have many more muscles (more creatinine produced) can theoretically exceed their body weight. Admitting the volume change in the equation, the calculation of volume distribution is impossible. Yet the volume shift exists in the perioperative stage; the assumption that ‘v’ is a constant value through the equation is essential for supporting the equation in this study.
This study has several limitations. First, this study is based on retrospective data collection from kidney transplant recipients. In fitting the model equations, the same data were used to calculate the coefficients of the model for each individual. These coefficients vary significantly among individual recipients, and these are not revealed until the data have been collected and can be retrospectively calculated. Therefore, this study is not suitable for predicting GFR in real time and providing the concepts of renal graft function after transplantation along with a renal graft recovery pattern. Second, the mathematical models in this study have the following limitations. First, equation 5 cannot explain the measured Scr under two conditions. First, if the kidney graft is injured after transplantation, dCdt decreases to less than 0, so the Scr level predicted using equation 5 does not fit the measured Scr (9.0% of population) because this equation was developed under the assumption that dCdt>0 at all times. Second, if a patient is treated with dialysis after transplantation, creatinine is artificially eliminated from blood, and the resulting substantial amount of extra-renal creatinine output results in a lack of fit with the predictions obtained with equation 5 (4.2% of population).
In conclusion, the proposed equations can provide a new perspective on calculating the renal function during the early phases of kidney transplantation. Furthermore, these equations may be helpful for understanding the functional recovery patterns of kidney transplantation and assessing DGF pathophysiology. Nevertheless, these equations were specialized to analyze the renal function in kidney transplant recipients in an early period, and a study on the correlation between the equations and long-term graft outcomes is needed in the future.
Go to : 




 PDF
PDF Citation
Citation Print
Print



 XML Download
XML Download