Abstract
Artificial intelligence has been applied to many industries, including medicine. Among the various techniques in artificial intelligence, deep learning has attained the highest popularity in medical imaging in recent years. Many articles on deep learning have been published in radiologic journals. However, radiologists may have difficulty in understanding and interpreting these studies because the study methods of deep learning differ from those of traditional radiology. This review article aims to explain the concepts and terms that are frequently used in deep learning radiology articles, facilitating general radiologists' understanding.
As artificial intelligence (AI) rapidly evolves, the fields to which it can be applied are also expanding to various industries worldwide. This has led to substantial advances in the specific fields, such as web search, self-driving cars, natural language processing, and computer vision. AI has also been applied in the medical field. AI is a branch of computer science devoted to creating systems to perform tasks that typically require human intelligence (1). AI is a term that encompasses various techniques. Among them, machine learning is a field of study that gives computers the ability to learn patterns from data without being explicitly programmed. Deep learning is a subset of machine learning that uses multiple layers to progressively extract higher-level features from raw input (Fig. 1). Deep learning is the most popular technique in the medical imaging field, especially for image classification, lesion detection, and segmentation (234). Studies using deep learning, also in the field of radiology, have been increasing with a rapidly growing propensity. Hence, many articles on deep learning have been published in radiology journals. However, the methods used differ between these studies and conventional clinical radiologic studies. The most significant difference is that the deep learning study, includes the process of developing algorithms. In this process, several concepts and terms unfamiliar to radiologists are used. As a result, radiologists who are not accustomed to deep learning may have difficulty in understanding and interpreting these studies. Therefore, in this review article, we aim to simplify the concepts and terms that frequently appear in deep learning radiology papers. We hope that this article will help general radiologists understand and interpret deep learning papers as well as make communication easier when collaborating with deep learning scientists.
Ground truth is a term used in various fields to refer to data and/or methods related to a greater consensus or to reliable values/aspects that can be used as references (5). In deep learning, it usually refers to “correct labels” prepared by experts. However, in practice, it is often difficult to make correct labels. For example, when developing an algorithm to diagnose pneumonia in chest radiography, the ground truth is whether there is pneumonia in the chest radiography. In this task, there are two ways to make labels. One is a method by which radiologists review images to make labels and the other is a method based on radiologic reports. In the former case, a lot of time and effort is required and there may be an inter-reader disagreement on the label. In the latter case, the correctness of the labels itself may not be satisfactory.
Data curation is the organization and integration of data collected from various sources to add value to the existing data. Data curation includes all the processes necessary for principled and controlled data creation, maintenance, and management. Medical imaging data curation may include data anonymization, checking the representative of the data, unification of data formats, minimizing noise of the data, annotation, and creation of structured metadata such as clinical data associated with imaging data.
Acquiring large amounts of good-quality data is often difficult in clinical radiology. Data augmentation is an approach that alters the training data in a way that changes the data representation while keeping the label the same. It provides a way to artificially expand a dataset and maximize the usefulness of a well-curated image dataset. Popular augmentations of image data include blurring or skewing an image, modifying the contrast or resolution, flipping or rotating the image, adjusting zoom, and changing the location of a lesion (6). These strategies essentially present a slightly different appearance of the same finding and can make a deep learning algorithm more robust and generalizable.
Collected data are typically divided into three subsets according to their usage: training, validation, and test dataset. The training data are used to train and optimize the parameters of the model. The validation data are used to monitor the performance of the model during the training and to search for the best model. The test data are used to finally evaluate the performance of the developed model. It is crucial to divide the data to avoid any overlap between the training or validation datasets and the test dataset in terms of generalization of developed models. The required size of the dataset for training deep learning models depends on the nature and complexity of the task.
Programming language includes a vocabulary and a set of grammatical rules for instructing a computer to perform specific tasks. Popular programming languages include Python, Java, C, C++, C#, JavaScript, R, and MATLAB. The popularity of each programming language can be found on the TIOBE website (7). The deep learning framework is a collection of programs that facilitate the design, training, and validation of deep neural networks through a high-level programming interface. It supports massive arithmetic computation in the form of vectors, matrices, or multi-dimensional tensors on the latest graphics processing unit (GPU). Frameworks are generally written in a specific programming language. The popularity of Python is rising in the field of deep learning and data analysis owing to its ease of learning and the availability of many helpful deep learning libraries and frameworks written in python. There are several deep learning frameworks such as TensorFlow, Keras, PyTorch, Caffe, Theano, MXNet, and CNTK (8910). Google's TensorFlow and Facebook's PyTorch have been the most popular in recent times. Keras and Caffe will be merged into TensorFlow and PyTorch, respectively, in their next release. Theano has been deprecated and is no longer being maintained.
The terms “parameter” and “hyperparameter” frequently appear in papers on deep learning. A parameter refers to a variable that is automatically adjusted during the model training. In general, weight is used as the same term as a parameter. However, weight is sometimes used as a sub-concept of a parameter in a convolutional neural network (CNN) to distinguish it from another term, “kernel.” In this case, weight refers to the parameters of a fully connected layer of CNN and kernel refers to the parameters of a convolutional layer of CNN. (The layers of CNN will be highlighted in the section, Convolutional Neural Network). Furthermore, a “hyperparameter” is a variable used to design the deep learning model and is a variable to be set before training the model. Hyperparameters in a CNN include kernel size, the number of kernels, stride, padding, activation function, pooling method, model architecture, optimizer, learning rate, cost function, batch size, and epochs. Some of these hyperparameters will be highlighted later in this paper.
CNN is one of the artificial neural networks that can be characterized by a convolutional layer, which differs from other neural networks (Fig. 2). A typical CNN is composed of a convolutional layer, a pooling layer, and a fully connected layer (11). The convolutional layer is the core of a CNN. In mathematical terms, “convolution” refers to the mathematical combination of two functions to produce a third function. When used in a CNN, convolution means that a kernel (or filter = small matrix) is applied to the input data to produce a feature map (Fig. 3). The convolution operation has been widely used in image processing such as edge detection, sharpening, blurring, and so on. Through this process, different characteristics of the input images are extracted at different levels. The next step, pooling, is a down-sampling operation that reduces the in-plane dimension of the feature maps. The two common pooling methods are average pooling and max pooling method. Average pooling calculates the average value in the target area while max pooling extracts the maximum value in the target area. The fully connected layers (dense layers) map the features extracted by both the convolutional layers and the pooling layers to the final outputs of the model. One of the important components of CNN is an activation function. The activation function transforms the outputs of linear operations such as convolutions nonlinearly making the neural network capable of learning and performing more complex tasks. Although sigmoid or hyperbolic tangent functions were used previously, the most common nonlinear activation function is the rectified linear unit (ReLU) function. CNN is the most widely used deep learning model in medical image analysis for the following reasons (12). First, CNN is more efficient in terms of the number of parameters to be trained. In other regular neural networks, each layer is fully connected to all neurons in the next layer. The fact that two neurons are connected indicates that there is a parameter to be trained between the two neurons (not considering bias). Therefore, the number of parameters to be trained is huge in these regular neural networks. On the other hand, the neurons in one layer of CNN do not connect to all the neurons in the next layer but only to a small region of neurons in the next layer through the same kernel in the convolutional layers of CNN. In other words, the only parameters to be trained in the convolutional layers are the kernel in the convolutional layers. As a result, the number of parameters can be reduced in CNN. For example, when there is an input layer of 256 × 256 and an output layer of 256 × 256, there are a total of 42,9496,7296 ([256 × 256] × [256 × 256]) parameters in fully connected neural networks. On the other hand, if a 3 × 3 kernel is used in CNN, there are only 9 parameters that need to be trained. (Here we assume that the number of channels is only 1, i.e., gray-scale image.). Second, relevant features can be learned from an image (feature learning). In traditional image processing such as blurring or sharpening, kernels of the function are specific pre-defined filters. For example, smartphone applications can be used to make an original photo blurred or sharpened by using filters. In CNN, however, kernels are not pre-defined but are trained to perform a specific task from raw data. Kernels that are determined as the result of training are applied to the input images, then various feature maps at different levels are produced in the CNN. Third, CNN is more efficient for a completely new task because an already trained CNN (with trained parameters from another task, a concept that will be explained in more detail in transfer learning) can be slightly tuned for the new task. Finally, CNN has outperformed other algorithms on image analysis especially in pattern and image recognition applications until now. For example, all winners of the ImageNet Large Scale Visual Recognition Challenge (ILSVRC) that used CNN-based models, AlexNet, won the challenge in 2012 (12).
Recurrent neural network (RNN) is a class of neural networks effective at processing sequential inputs such as language, speech, and time-series data. In the radiologic field, RNN can be applied within domains such as electronic health records, including radiologic reports (1314). Generative adversarial network (GAN) is another deep learning algorithm where two neural networks of the generator and the discriminator compete and cooperate with each other. In the radiology field, GAN has been applied to synthesize realistic medical images (1516).
As mentioned above, one of the advantages of CNN is its ability to use the pre-trained CNN models. Many recent studies have developed models based on these pre-trained CNN models. For tasks related to object recognition, many CNN models have been developed through the ILSVRC, which is an annual software competition conducted by the ImageNet project. The CNN models of the top competitors of ILSVRC include LeNet, AlexNet, ZFNet, GoogLeNet/Inception, VGG Net, DenseNet, and ResNet. Tasks related to segmentation include U-Net and Mask-RCNN (121718192021222324).
Transfer learning is the process of taking a pre-trained model and “fine-tuning” the model with a new dataset (Fig. 4). The idea is that this pre-trained model acts as a feature extractor. More specifically, the pre-trained CNN models of the ILSVRC extract features such as edges and curves for object detection and image classification. Unless a new task differs totally from the ImageNet project in the dataset and the problem, the layers of the pre-trained model can be reused for feature extraction. Fully connected layers, with or without parts of the kernels of the convolutional layers of the pre-trained model, are then replaced with a new set and are trained with the dataset of the new task. Transfer learning can lessen the data demands for development of CNN models because the number of parameters for training can be reduced by reusing the parameters of the pre-trained models. Transfer learning can be useful in radiology since the number of medical images is usually limited.
Cost (loss) is the difference (not necessarily a mathematical difference) or compatibility between the true values (ground truth) and the values predicted by the model. A cost function (loss function) is a function comprising the true value and the predicted value and it is used to measure cost. The choice of the cost function used is determined based on the given tasks. Cross entropy and mean squared error are commonly used cost functions for classification tasks and regression tasks, respectively.
Forward propagation is a process used to calculate the predicted value from input data through the model. Back propagation is a process used to adjust each parameter of the model to minimize the cost (Fig. 5).
Model training is a process of parameter optimization used to minimize the difference between the true value and the model's predicted value. In CNN, the gradient descent method is used for parameter optimization, which further uses the gradient and learning rate to adjust the parameters. (Fig. 6). The gradient is a derivative of the cost function at a specific value of the parameter. The learning rate is a hyperparameter that controls how much the parameters of the model are adjusted. It is crucial to set the learning rate to an appropriate value. If the learning rate is very small, the model will converge too slowly. Conversely, if the learning rate is too large, the model will diverge (Fig. 7). There are three types of gradient descent that primarily differ in how much data are used to compute the gradient of the cost function. Batch gradient descent refers to calculating the derivative from all training data before calculating an update. Stochastic gradient descent (SGD) refers to calculating the derivative from each training data instance and calculating the update immediately. Finally, mini-batch gradient descent takes the best of batch gradient descent and SGD and performs an update for every mini-batch of n-training examples. Optimizing parameters with the gradient descent method may lead to problems when the same learning rate is uniformly applied to all parameters. Therefore, several algorithms have been developed for the optimization of the gradient and learning rate that need to be applied. These gradient descent optimization algorithms include SGD with momentum, Nesterov accelerated gradient, Adagrad, Adadelta, Adaptive Moment Estimation, and AdaMax (2526272829). However, none of them has a clear advantage over the other. The gradient descent optimization algorithm (the optimizer) is one of the important hyperparameters that must be determined in the model training process.
In general, the entire large dataset cannot pass into the neural network at once. Therefore, the dataset should be divided in order to pass. An Epoch refers to one forward pass and one backward pass of all the training data through the model. Usually, we repeat several epochs to train a model. Batch size is the fixed number of training data in one forward/backward pass. Batch size is determined by considering the total size of the dataset, the number of weights in the model, and the available memory of the GPU. Batch size usually ranges from 1 to 128. The higher the batch size, the more memory space will be needed. The number of iterations is the total number of passes (Fig. 8).
An ensemble of models implies to train multiple models by varying architectures, hyperparameter settings and training techniques and to combine predictions of each model. This method generally improves prediction performance compared to that of a single model.
Although the final performance of the model is determined by its performance on a test dataset, there is no means to predict how well a model will perform until its performance is tested on a test dataset. Cross-validation is a technique employed to estimate the performance of models in the “training” phase to check for overfitting and to get an idea about how the models will generalize to the given test dataset. In k-fold cross-validation, the training dataset is partitioned into k equal subsets. One data subset is kept as the validation set, and the others (k-1 subsets) are kept as a cross-validation training set. The model is then trained using the cross-validation training set, and the performance of the model is evaluated using the validation set. This process is repeated a total of k times while changing the validation set. The results from all the rounds are averaged to estimate the performance of the model.
For a classification task, receiver operating characteristic (ROC) curves are used for the model performance measurement. For a segmentation task, the Dice score (Sørensen-Dice coefficient = F1 score) and the Jaccard index (Jaccard similarity coefficient, Jaccard score = Intersection over Union) are used for model performance measurement (Fig. 9). In addition, the true positive rate = sensitivity = recall, true negative rate = specificity, false-positive rate, and false-negative rate can be used for model performance measurement depending on the given tasks.
This review article discusses the basic concepts of deep learning, especially CNN, and its commonly used terms. Radiologists who familiarize themselves with its concepts and terms will be better prepared to understand deep learning articles and to communicate with deep learning scientists.
Figures and Tables
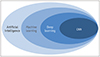 | Fig. 1Diagram of artificial intelligence hierarchy.Machine learning is field of study that gives computers ability to learn without being explicitly programmed. Deep learning is subset of machine learning that makes computation of multi-layer neural networks feasible. CNN is subset of deep learning characterized by convolutional layer. CNN = convolutional neural network
|
 | Fig. 2Schematic diagram of CNN model and other regular neural networks.
A. CNN includes convolutional layers, pooling layers, and fully connected layers. B. Each layer is fully connected to all neurons in next layer in other regular neural networks. Conv = convolution
|
 | Fig. 3Convolution and pooling.
A. Example of convolution and pooling. Convolution implies that kernel is applied to input image to produce feature map. Pooling is down-sampling operation. Input, kernel, and feature map are all expressed by matrices, and convolution and pooling are both matrix operations. In this example, a kernel (2 × 2) is applied across input data and element-wise product between kernel and input data is first calculated at each location and then summed to obtain output value in corresponding position of feature map (1 × 1 + 2 × 1 + 5 × 1 + 6 × 1 = 14). In pooling operation, max pooling with filter size of 2 × 2 is applied. Among four values (14, 18, 30, and 34), maximum value (34) is output in corresponding position of next layer. B. Visualization of feature maps through multi-step convolution and pooling. Example of visualized feature maps with chest radiographic image as input for task to differentiate between abdominal and chest radiographs.
|
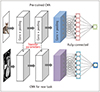 | Fig. 4Transfer learning.Transfer learning is process of taking pre-trained model (usually trained on large dataset, such as ImageNet) and “fine-tuning” model with new dataset. Fully connected layers, with or without parts of kernels of convolutional layers of pre-trained model are replaced with new set and are trained with dataset of new task.
|
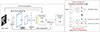 | Fig. 5Model training.Model training is process of parameter (kernel + weight) optimization through forward and back propagation. Forward propagation is process used to calculate predicted value from input data through model. Back propagation is process used to adjust each parameter of model toward minimizing cost. When presenting series of training samples to model, difference between predicted value and ground truth (target class or regression value) is measured using cost function. Using gradient descent method, all parameters (weights in fully connected layer and kernels in convolutional layer) are slightly adjusted to minimize cost.
|
 | Fig. 6Gradient descent.Gradient descent is optimization algorithm used to identify parameters that minimize cost. Parameter is repeatedly updated until cost reaches minimum with following formula: Wb = Wa − (learning rate) × (gradient). Optimal parameter of model is value that minimizes cost most.
In graph (A), gradient is negative at initial value of parameter (a), and value of (− learning rate × gradient at Wa) is positive. As result, parameter is updated toward increasing value. By repeating this process, minimum of cost function (c) can be obtained, which is parameter's optimal value. On the other hand, gradient is positive at initial value of parameter (a) in graph (B) and value of (− learning rate × gradient at Wa) is negative. As result, parameter is updated in direction of decreasing value, and minimum of cost function (c) is reached. Using gradient descent method, parameter can be optimized regardless of parameter's initial value (initial values of parameters are commonly randomly set). Letter “W” is derived from weight and weight is same as parameter in this case.
|
 | Fig. 7Effect of learning rate on model training.Learning rate is hyperparameter that determines degree of parameter update. It is important to set learning rate to appropriate value. If learning rate is too small, model will converge too slowly. On the other hand, if learning rate is too large, model will diverge without convergence. Letter “W” is derived from weight and weight is same as parameter in this case.
|
 | Fig. 8Epoch, batch, and iteration.There is dataset of 6 images. In C, batch size is 2, and algorithm is set to run for 2 epochs. Therefore, in each epoch, there are 3 batches (6 / 2 = 3). Each batch gets passed through algorithm, so there are 3 iterations per epoch. Since 2 epochs were specified, there are total of 6 iterations (3 × 2 = 6) for training. In A, batch size, epoch, and iteration are 3, 1, and 2, respectively. In B, batch size, epoch, and iteration are 2, 1, and 3, respectively.
|
References
1. Chartrand G, Cheng PM, Vorontsov E, Drozdzal M, Turcotte S, Pal CJ, et al. Deep learning: a primer for radiologists. Radiographics. 2017; 37:2113–2131.


2. Litjens G, Kooi T, Bejnordi BE, Setio AAA, Ciompi F, Ghafoorian M, et al. A survey on deep learning in medical image analysis. Med Image Anal. 2017; 42:60–88.


3. Dreyer KJ, Geis JR. When machines think: radiology’s next frontier. Radiology. 2017; 285:713–718.


4. Soffer S, Ben-Cohen A, Shimon O, Amitai MM, Greenspan H, Klang E. Convolutional neural networks for radiologic images: a radiologist's guide. Radiology. 2019; 290:590–606.


5. Cardoso JR, Pereira LM, Iversen MD, Ramos AL. What is gold standard and what is ground truth? Dental Press J Orthod. 2014; 19:27–30.

6. Zhong Z, Zheng L, Kang G, Li S, Yang Y. Random erasing data augmentation. eprint arXiv;2017. Accessed April 1, 2019. Available at: https://ui.adsabs.harvard.edu/abs/2017arXiv170804896Z.
7. TIOBE index for April 2019. TIOBE Web site;Accessed April 30, 2019. https://www.tiobe.com/tiobe-index/.
8. Jia Y, Shelhamer E, Donahue J, Karayev S, Long J, Girshick R, et al. Caffe: convolutional architecture for fast feature embedding. eprint arXiv;2014. Accessed April 1, 2019. Available at: https://ui.adsabs.harvard.edu/abs/2014arXiv1408.5093J.
9. Bastien F, Lamblin P, Pascanu R, Bergstra J, Goodfellow I, Bergeron A, et al. Theano: new features and speed improvements. eprint arXiv;2012. Accessed April 1, 2019. Available at: https://ui.adsabs.harvard.edu/abs/2012arXiv1211.5590B.
10. Abadi M, Barham P, Chen J, Chen Z, Davis A, Dean J, et al. TensorFlow: a system for large-scale machine learning. eprint arXiv;2016. Accessed April 1, 2019. Available at: https://ui.adsabs.harvard.edu/abs/2016arXiv160508695A.
11. Lee JG, Jun S, Cho YW, Lee H, Kim GB, Seo JB, et al. Deep learning in medical imaging: general overview. Korean J Radiol. 2017; 18:570–584.



12. Krizhevsky A, Sutskever I, Hinton GE. ImageNet classification with deep convolutional neural networks. Advances in Neural Information Processing Systems. 2012; 25:1090–1098.

13. Lee C, Kim Y, Kim YS, Jang J. Automatic disease annotation from radiology reports using artificial intelligence implemented by a recurrent neural network. AJR Am J Roentgenol. 2019; 212:734–740.


14. Girshick R, Donahue J, Darrell T, Malik J. Rich feature hierarchies for accurate object detection and semantic segmentation. eprint arXiv;2013. Accessed April 1, 2019. Available at: https://ui.adsabs.harvard.edu/abs/2013arXiv1311.2524G.
15. Kazuhiro K, Werner RA, Toriumi F, Javadi MS, Pomper MG, Solnes LB, et al. Generative adversarial networks for the creation of realistic artificial brain magnetic resonance images. Tomography. 2018; 4:159–163.



16. Goodfellow IJ, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, et al. Generative adversarial networks. eprint arXiv;2014. Accessed April 1, 2019. Available at: https://ui.adsabs.harvard.edu/abs/2014arXiv1406.2661G.
17. Ronneberger O, Fischer P, Brox T. U-net: convolutional networks for biomedical image segmentation. eprint arXiv;2015. Accessed April 1, 2019. Available at: https://ui.adsabs.harvard.edu/abs/2015arXiv150504597R.
18. Huang G, Liu Z, van der Maaten L, Weinberger KQ. Densely connected convolutional networks. eprint arXiv;2016. Accessed April 1, 2019. Available at: https://ui.adsabs.harvard.edu/abs/2016arXiv160806993H.
19. Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition. eprint arXiv;2014. Accessed April 1, 2019. Available at: https://ui.adsabs.harvard.edu/abs/2014arXiv1409.1556S.
20. He K, Zhang X, Ren S, Sun J. Deep residual learning for image recognition. eprint arXiv;2015. Accessed April 1, 2019. Available at: https://ui.adsabs.harvard.edu/abs/2015arXiv151203385H.
21. Szegedy C, Liu W, Jia Y, Sermanet P, Reed S, Anguelov D, et al. Going deeper with convolutions. eprint arXiv;2014. Accessed April 1, 2019. Available at: https://ui.adsabs.harvard.edu/abs/2014arXiv1409.4842S.
22. He K, Gkioxari G, Dollár P, Girshick R. Mask R-CNN. eprint arXiv;2017. Accessed April 1, 2019. Available at: https://ui.adsabs.harvard.edu/abs/2017arXiv170306870H.
23. Lecun Y, Bottou L, Bengio Y, Haffner P. Gradient-based learning applied to document recognition. Proceedings of the IEEE. 1998; 86:2278–2324.

24. Zeiler MD, Fergus R. Visualizing and understanding convolutional networks. eprint arXiv;2013. Accessed April 1, 2019. Available at: https://ui.adsabs.harvard.edu/abs/2013arXiv1311.2901Z.
25. Qian N. On the momentum term in gradient descent learning algorithms. Neural Netw. 1999; 12:145–151.


26. Nesterov YE. A method for solving the convex programming problem with convergence rate O(1/k2). Dokl Akad Nauk SSSR. 1983; 269:543–547.
27. Duchi J, Hazan E, Singer Y. Adaptive subgradient methods for online learning and stochastic optimization. J Mach Learn Res. 2011; 12:2121–2159.
28. Zeiler MD. ADADELTA: an adaptive learning rate method. eprint arXiv;2012. Accessed April 1, 2019. Available at: https://ui.adsabs.harvard.edu/abs/2012arXiv1212.5701Z.
29. Kingma DP, Ba J. Adam: a method for stochastic optimization. eprint arXiv;2014. Accessed April 1, 2019. Available at: https://ui.adsabs.harvard.edu/abs/2014arXiv1412.6980K.




 PDF
PDF ePub
ePub Citation
Citation Print
Print



 XML Download
XML Download