Exact solution for the kinetics of reversible reaction
Let us consider the following simple reversible reaction scheme
Where the first step is reversible with a forward rate constant k1 and reverse rate constant k2, and the second step is irreversible with the rate constant k3. The rate constant has the units of the amount per unit time, which are omitted for simplicity in this tutorial. The rate equations are:
Linear ordinary differential equations can be solved using Laplace transformation or the matrix method.[
23712] We used the latter to obtain an exact solution because of its simplicity. The above expressions can be written in matrix form:
By setting
|−k1−λk20k1−(k2+k3)−λ00k3−λ|=0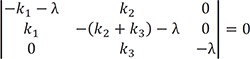
, where λ is the eigenvalue, and solving for λ, we get the following characteristic polynomial:
Where p = k1 + k2 + k3 and q = k1k3. The solutions of the quadratic equation in Eq. (5) are given by
and
The resulting eigenvalues are 0, −α, and −β. These eigenvalues are substituted into the eigenvalue equation to yield the corresponding eigenvectors of
[001], [β−k1k1β], and [α−k1k1α]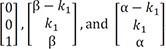
, spectively.
Because the matrix M has three distinct real eigenvalues and their corresponding eigenvectors, we can express the solution as
At t = 0, A = A0 and B = C = 0, and A + B + C = A0 at all times. Using these boundary conditions, we can solve Eq. (6) to get C0 = A0, C1 = −C2 and C1 = A0/(β – α). Then, the final expressions for the above differential equations (1–3) are
We can compare these results to those for a consecutive two-step reaction, as described in the previous tutorial.[
13] We can easily show that the latter has the eigenvalues of 0, −
k1, and −
k3, by setting
k2 = 0 in Eq. (5). The solutions for
B and
C, equations 8 and 9 in this study, are very similar to those for the consecutive reaction (Equations 7 and 9 in Reference,[
13] respectively). Thus, the expressions for the maximum amount of
B (
Bmax) and the time to reach the peak (
tmax) can be obtained in a similar way:
and
respectively.
Graphical insights into the kinetics of reversible reactions
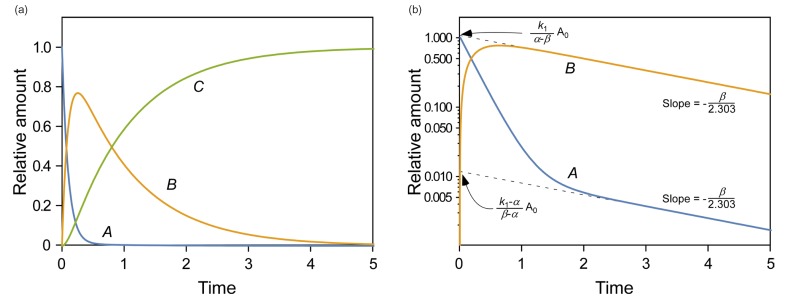
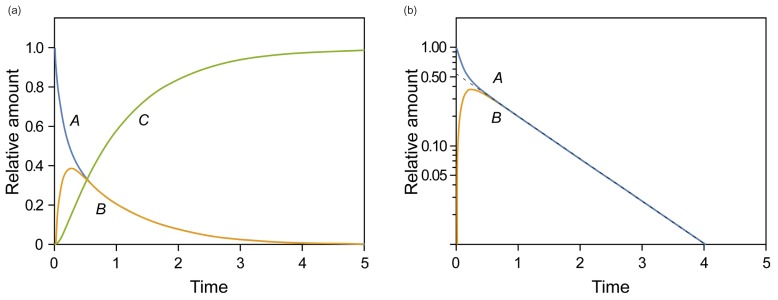
Figure 1 shows representative amount versus time curves of
A,
B, and
C, plotted on a linear and semi-logarithmic scale for three different cases: (a)
k1 = 10,
k2 = 0.1, and
k3 = 1; (b)
k1 = 5,
k2 = 4, and
k3 = 2; (c)
k1 = 1,
k2 = 5, and
k3 = 0.2. When
k1 and
k3 are relatively larger than
k2, that is, the reverse reaction is negligible, linear plots of the amount versus time curves of
A and
B for the reversible reaction (
Fig. 1a) look very similar to those for a consecutive irreversible reaction (see
Figure 2 in Reference[
13]). The semi-logarithmic plots for the former case (
Fig. 1b), however, look different from those for the latter case (see
Figure 3a in Reference[
13]). In the former case, two curves are always parallel to each other in the elimination phase, whereas they are not in the latter case. The difference can be explained as follows. For an irreversible reaction, the amount of
A is described by one exponential term, whereas for the reversible reaction, it is described by two exponential terms. For the latter, the first term in Eq. (7) or (8) decreases faster than the second term over time, because α is always larger than β. This means that the elimination phase is governed by the second term. Therefore, the first term can be neglected when
t is sufficiently large. In semi-logarithmic plots of
A and
B, thus, both slopes for the elimination phase are linear and identical and given by –β/2.303. The y-intercepts for
A and
B are
α−k1α−βA0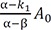
and
k1α−βA0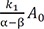
, respectively. When 2
k1 = 2
k2 +
k3, the intercepts are the same, as shown in
Figure 2. If 2
k1 < 2
k2 +
k3, the curves
A and
B will not cross each other. As a third case, we set
k1 = 1,
k2 = 5, and
k3 = 0.2, which satisfies this condition. It is noteworthy that the semi-logarithmic plots for this case (
Fig. 3b) strongly resemble those for the consecutive irreversible reaction (see
Figure 3b in Reference[
13]). In the latter case, the semi-logarithmic plots of plasma concentrations versus time of A and B become parallel straight lines at large
t only when the formation rate of B is much slower than its elimination rate; that is, the metabolism is formation rate-limited (FRL).[
131415] In addition, the intercept for [B] becomes greater than that for [A] when the distribution volume of
B,
VB, is much smaller than that of
A,
VA (see
Figure 3c in Reference[
13]). However, we need to be cautious when we apply this feature to the interpretation of the time profiles of the semi-logarithmic plots of a drug and its metabolite because this feature is commonly observed in reversible metabolic reactions. The pharmacokinetic parameters for each case, including
tmax and
Bmax, are summarized in
Table 1.
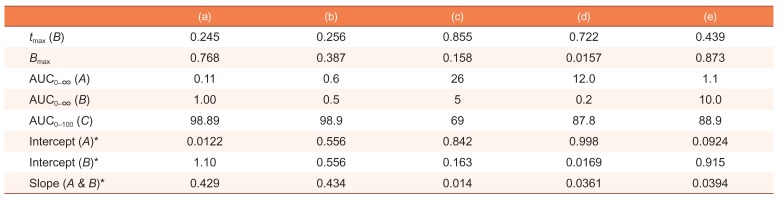
Table 1
Pharmacokinetic parameters for the following cases: (a) k1 = 10, k2 = 0.1, and k3 = 1 (as in Fig. 1); (b) k1 = 5, k2 = 4, and k3 = 2 (as in Figure 2); (c) k1 = 1, k2 = 5, and k3 = 0.2 (as in Figure 3); (d) k1 = 0.1, k2 = 1, and k3 = 5, (as in Figure 4a); (e) k1 = 10, k2 = 1, and k3 = 0.1 (as in Figure 4b)
|
(a) |
(b) |
(c) |
(d) |
(e) |
|
tmax (B) |
0.245 |
0.256 |
0.855 |
0.722 |
0.439 |
|
Bmax
|
0.768 |
0.387 |
0.158 |
0.0157 |
0.873 |
|
AUC0–∞ (A) |
0.11 |
0.6 |
26 |
12.0 |
1.1 |
|
AUC0–∞ (B) |
1.00 |
0.5 |
5 |
0.2 |
10.0 |
|
AUC0–100 (C) |
98.89 |
98.9 |
69 |
87.8 |
88.9 |
|
Intercept (A)*
|
0.0122 |
0.556 |
0.842 |
0.998 |
0.0924 |
|
Intercept (B)*
|
1.10 |
0.556 |
0.163 |
0.0169 |
0.915 |
|
Slope (A & B)*
|
0.429 |
0.434 |
0.014 |
0.0361 |
0.0394 |

The area under the curve (AUC) is an important pharmacokinetic parameter, representing total drug exposure over time. The AUC for A and B can be obtained by directly integrating Eqs. (7) and (8) from zero to infinity, respectively, and expressed as
Thus, the ratio of AUC
A to AUC
B can be simplified to
k2+k3k1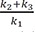
. The AUC for C can also be calculated by integrating Eq. (9) from zero to
t and given by
Using a time integration method,[
1416] we can obtain the relationship between AUC and rate constant or clearance, which has the units of volume (V) per unit time (CL =
k × V). By separating the variables in Eqs. (7–9) and integrating both sides with respect to their respective variables, we can write the equations as follows:
They should satisfy the following boundary conditions: [B] = [C] = 0 at t = 0; [A] = [B] = 0 and VC × [C] = A0 at t = ∞. By substituting k1 = CL1/VA, k2 = CL2/VB, and k3 = CL3/VC, we get
Eq. (19) can be rearranged as
These relationships are helpful in understanding pharmacokinetic features and metabolic pathways.[
141718]
Approximation of the kinetics of reversible reactions
To get a good approximate solution for a reversible reaction scheme, approximation approaches have been developed and are widely used.[
121920] Depending upon the reactivity of the intermediate species, we can use either of two approximation approaches. One is a steady-state approximation, in which the intermediate species
B is very reactive and hence short lived. This approximation is useful for explaining reactions involving radical species. The other is an equilibrium approximation, in which B is quite stable and long-lived because the equilibrium reaction proceeds faster than the product formation reaction; that is,
k1,
k2 >>
k3. For both approaches, the following condition should be satisfied:
In the steady-state approximation, B is extremely unstable and very short-lived and thus is present in most of the time in extremely small amounts. By assuming that B ≈ 0, we can get a new boundary condition: A + C = A0. From Eq. (22), Eq. (2) can be rearranged to yield:
For the steady-state approximation, this ratio should be very small because the amount of B is much smaller than that of A. Substituting Eq. (23) into Eq. (1) and re-arranging it for A, we have
By separating the variables and integrating the resulting equation, we get
Using the above expression and the new boundary condition, A + C = A0, we obtain
Now we can solve Eq. (2) for B using Eq. (26), to get
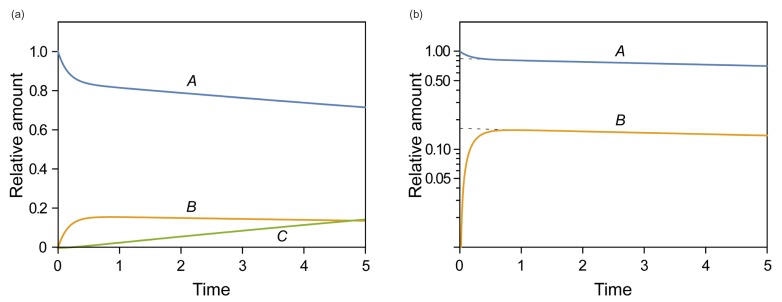
We plot the exact and approximate solutions for the case where
k1 = 0.1,
k2 = 1, and
k3 = 5 (
Fig. 4a). Because
k1k2+k3=0.11+5~0.017≪1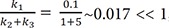
, the requirement for the steady-state approximation is satisfied. As the reaction begins, the amount of B quickly increases but is still extremely small (
Bmax = 0.016 at
tmax = 0.72) for most of the time, as expected. As shown in
Figure 4a, the approximate solutions (dashed lines) agree well with the exact solutions (solid lines).
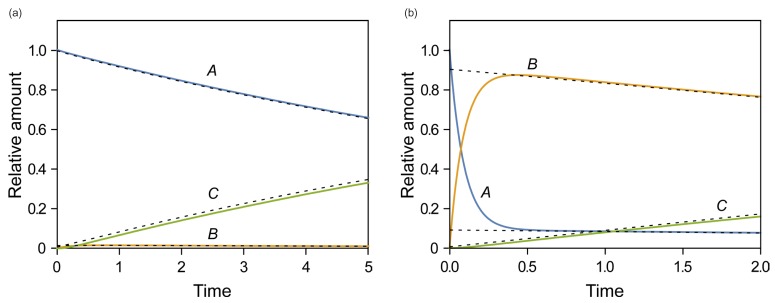 | Figure 4Linear plots of the amount-time curves of A, B, or C for the cases of (a) k1 = 0.1, k2 = 1, and k3 = 5, corresponding to the steady-state approximation, and (b) k1 = 10, k2 = 1, and k3 = 0.1, corresponding to the equilibrium approximation. The solid and dashed lines represent the exact and approximate solutions, respectively. The abscissa and ordinate denote time and the amount of each species, respectively, in arbitrary unit. See text for details.
|
For the equilibrium approximation, the reaction needs to be in pseudo-equilibrium. In such a case, we can express
Where Keq is an equilibrium constant. Because
we also have
Because of the above condition, it is not feasible to directly solve Eqs. (1) and (2). Instead, we need to combine the two equations to get
If we define X = A + B = A0 – C, from Eq. (28), we can express A and B as
Now Eq. (30) can be solved for X to get
Then, we have
In
Figure 4b, we show the plots of the exact and approximate solutions for the case where
k1 = 10,
k2 = 1, and
k3 = 0.1. Unlike in
Figure 4a, the amount of B is not negligible (
Bmax = 0.87 at
tmax = 0.44). The reaction rapidly reaches quasi-equilibrium, after which the amount of B slowly decreases. As shown in
Figure 4b, the approximate solutions (dashed lines) agree well with the exact solutions (solid lines).
The difference between steady-state and equilibrium approximate approaches lies in the range of their applicability. [
20] When we introduce an additional constraint,
k2 >>
k1 into the equilibrium approach and
k2 >>
k3 into the steady state approach, both methods will yield the same solution.[
20] This relationship can be further explained by considering an approximate expression for β. Using the following binomial theorem
we can obtain the binomial expansion of β, which yields
If k1 + k2 >> k3 or k2 + k3 >> k1, the second and higher order terms in the expansion can be negligible, and the first term can be further simplified to be the same as the exponent in the equilibrium approximation [see Eqs. (33–35)] or in the steady-state approximation [see Eqs. (25–27)], respectively. For a refined approximation, we can differentiate Eq. (23) for A and B with respect to time t to get
By substituting Eqs. (3), (23), and (37) into Eq. (29) and rearranging the resulting equation, we get
We expect a better approximate solution from the above equation compared with that produced by Eq. (24).
Application of the Reversible Reaction Scheme
The reversible reaction scheme is also used to describe drug distribution after rapid intravenous injection. Drug distribution within the body is often described by a two-compartment model with central and peripheral compartments.[
21] In this model, an injected drug will be either eliminated or distributed within the central compartment, representing intravascular space, and the peripheral compartment, representing non-metabolizing body tissues. The distribution phase can be expressed by two linear differential equations similar to Eqs. 1 and 2.[
21] The solution for drug concentration in each compartment can be obtained using a similar approach and described by two exponential terms.
To explain the kinetics of an enzyme-catalyzed reaction, a Michaelis-Menten model has been widely used.[
222324] When an enzyme and a substrate form a complex, the binding of the substrate to the active site of the enzyme is non-covalent and reversible. If the conversion of the enzyme-substrate complex to a product is the rate-limiting process, the concentration of the complex can be considered to be constant. Then, the equilibrium approximation will give a hyperbolic relationship between the initial reaction rate, v_0, and substrate concentration [
S], known as the Michaelis-Menten equation,
Where
Vmax is the maximum reaction rate achieved when all of the active sites are occupied by substrates. The Michaelis constant, in the original article,[
2223] is given by
KS=k2k1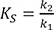
. When a steady-state approximation is used, the constant is given by
Km=k2+k3k1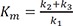
. [
24]
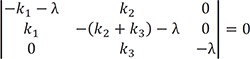 , where λ is the eigenvalue, and solving for λ, we get the following characteristic polynomial:
, where λ is the eigenvalue, and solving for λ, we get the following characteristic polynomial: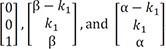 , spectively.
, spectively.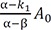 and k1α−βA0
and k1α−βA0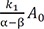 , respectively. When 2k1 = 2k2 + k3, the intercepts are the same, as shown in Figure 2. If 2k1 < 2k2 + k3, the curves A and B will not cross each other. As a third case, we set k1 = 1, k2 = 5, and k3 = 0.2, which satisfies this condition. It is noteworthy that the semi-logarithmic plots for this case (Fig. 3b) strongly resemble those for the consecutive irreversible reaction (see Figure 3b in Reference[13]). In the latter case, the semi-logarithmic plots of plasma concentrations versus time of A and B become parallel straight lines at large t only when the formation rate of B is much slower than its elimination rate; that is, the metabolism is formation rate-limited (FRL).[131415] In addition, the intercept for [B] becomes greater than that for [A] when the distribution volume of B, VB, is much smaller than that of A, VA (see Figure 3c in Reference[13]). However, we need to be cautious when we apply this feature to the interpretation of the time profiles of the semi-logarithmic plots of a drug and its metabolite because this feature is commonly observed in reversible metabolic reactions. The pharmacokinetic parameters for each case, including tmax and Bmax, are summarized in Table 1.
, respectively. When 2k1 = 2k2 + k3, the intercepts are the same, as shown in Figure 2. If 2k1 < 2k2 + k3, the curves A and B will not cross each other. As a third case, we set k1 = 1, k2 = 5, and k3 = 0.2, which satisfies this condition. It is noteworthy that the semi-logarithmic plots for this case (Fig. 3b) strongly resemble those for the consecutive irreversible reaction (see Figure 3b in Reference[13]). In the latter case, the semi-logarithmic plots of plasma concentrations versus time of A and B become parallel straight lines at large t only when the formation rate of B is much slower than its elimination rate; that is, the metabolism is formation rate-limited (FRL).[131415] In addition, the intercept for [B] becomes greater than that for [A] when the distribution volume of B, VB, is much smaller than that of A, VA (see Figure 3c in Reference[13]). However, we need to be cautious when we apply this feature to the interpretation of the time profiles of the semi-logarithmic plots of a drug and its metabolite because this feature is commonly observed in reversible metabolic reactions. The pharmacokinetic parameters for each case, including tmax and Bmax, are summarized in Table 1.
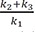 . The AUC for C can also be calculated by integrating Eq. (9) from zero to t and given by
. The AUC for C can also be calculated by integrating Eq. (9) from zero to t and given by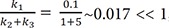 , the requirement for the steady-state approximation is satisfied. As the reaction begins, the amount of B quickly increases but is still extremely small (Bmax = 0.016 at tmax = 0.72) for most of the time, as expected. As shown in Figure 4a, the approximate solutions (dashed lines) agree well with the exact solutions (solid lines).
, the requirement for the steady-state approximation is satisfied. As the reaction begins, the amount of B quickly increases but is still extremely small (Bmax = 0.016 at tmax = 0.72) for most of the time, as expected. As shown in Figure 4a, the approximate solutions (dashed lines) agree well with the exact solutions (solid lines).




 PDF
PDF ePub
ePub Citation
Citation Print
Print



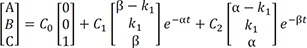
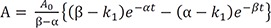
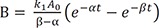
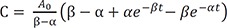
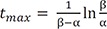
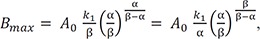
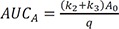
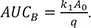
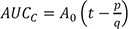
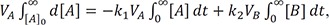
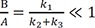
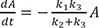
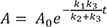
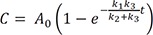
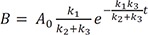
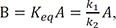
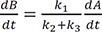
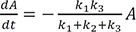
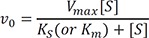
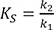
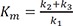
 XML Download
XML Download