An analytical solution is not a numerical solution, and it can calculate concentrations at any time point without calculating the intervening time points (if the input function was not changed meanwhile). On the contrary, it is necessary to calculate concentrations of intervening many time points if one has only a numerical solution (in other words, if you use numerical integration).
If a drug is administered without previous dosing and not an endogenous substance, the drug concentration at time 0 (initial condition) will be zero. However, if the drug is cleared insufficiently from the previous dose or an endogenous substance, the drug concentrations of each compartment at time 0 (the initial condition) would not be zero. This condition is called non-zero initial condition here.
With zero initial values, it is not so difficult to have an analytical solution. And, if the pharmacokinetic model is a one-compartment model, Non-zero initial value problem can be solved without much difficulty using the rule of superposition for the drug amount (or concentration).
However, if the pharmacokinetic model is a multi-compartment model and the initial condition is not-zero for all compartments, one can not simply use the rule of superposition for the concentrations because the drug of each compartment moves between compartments.
For the simulation, numerical integration is often sufficient. However, for the fitting or estimation, an analytical solution is usually better because of the speed. Solutions with a single dose or zero-initial value are easily found in textbooks. However, solutions for the multi-compartment model with non-zero initial value are harder to find. Authors would like to present the most elegant way to solve this kind of problems analytically.
Case presentation
[Dosing history]
At 0-hour, 100 mg of a drug was administered by intravenous bolus.
At 24-hour, 150 mg of a drug was infused intravenously with the rate of 50 mg/hr.
At 48-hour, 100 mg of a drug was administered orally.
[Measurement time points]
The concentrations of a drug at 0, 1, 2, 4, 8, 12 hours after each dose with given pharmacokinetic parameters.
[Exercise 1. One-compartment model]
If the drug is disposed by a one-compartment model with the pharmacokinetic parameters of Ka = 1, Ke = 0.1, F = 1, and V = 1, what will be the concentrations at the measurement time points?
[Exercise 2. Two-compartment model]
If the drug is disposed by a two-compartment model with the pharmacokinetic parameters of Ka = 1, Ke = K10 = 0.1, K12 = 3, K21 = 1, F = 1, and V = 1, what will be the concentrations at the measurement time points?
[Exercise 3. Three-compartment model]
If the drug is disposed by a three-compartment model with the pharmacokinetic parameters of Ka = 1, Ke = K10 = 0.1, K12 = 3, K21 = 1, K13 = 2, K31 = 0.5, F = 1, and V = 1, what will be the concentrations at the measurement time points?
The easiest way to solve the above problem is using the ‘wnl' R package. This package can be used to solve all of the pharmacokinetic and pharmacodynamic exercises in the pharmacokinetic textbooks or manuals. This can also be called in other packages for therapeutic drug monitoring, parameter estimation, pharmacokinetic or pharmacodynamic simulation. This package is for deterministic simulations, but not for stochastic ones. For a stochastic simulation, one needs to generate random pharmacokinetic parameters using multivariate distributions and random residuals.
To install this from the default repository, use the following command.
require(wnl)
# Solution 1
X1 = Comp1(Ke = 0.1, Ka = 1, DAT2) ; X1
matplot(DAT2[, “TIME”], X1, type = “l”)
# Solution 2
Sol = SolComp2(K10 = 0.1, K12 = 3, K21 = 1)
X2 = nComp(Sol, Ka = 1, DAT2) ; X2
matplot(DAT2[, “TIME”], X2, type = “l”)
# Solution 3
Sol = SolComp3(K10 = 0.1, K12 = 3, K21 = 1, K13 = 2, K31 = 0.5)
X3 = nComp(Sol, Ka = 1, DAT2) ; X3
matplot(DAT2[, “TIME”], X3, type = “l”)
The results of the above R script were confirmed with ADAPT 5 and NONMEM 7.4.3.
One can see all the source script with the following commands, and all the functions have only 20 to 40 lines for each.
ExpandDH # Expand Dosing History to include all non-differentiable points
Comp1 # One-compartment model with pharmacokinetic parameters
nComp # Multi-compartment model with lambdas and coefficients
SolComp2 # Solver for lambdas and coefficients of a 2-compartment model
SolComp3 # Solver for lambdas and coefficients of a 3-compartment model
There are many ways to solve this kind of problems. The strategy adopted here is that each amount at time ti will be calculated using the elapsed time (delta t) from the previous time point ti-1 and an initial condition equal to the condition (amounts of each compartment) of the previous time ti-1 point. This strategy is used for software such as NONMEM and ADAPT.
The list of terms related to the differential equation but not explained here are ordinary differential equation, initial value problem, coupled linear differential equation, homogenous differential equation, inhomogeneous differential equation, homogenous solution, particular solution, impulse response function, Laplace transformation, and convolution. The definitions and meaning of these terms can be found in textbooks or on the internet without difficulty.
Go to :

One-compartment model with non-zero initial condition
After intravenous bolus injection, the drug amount at time t, X(t) in the central compartment (or concentration if you divide the amount by the volume of distribution) can be calculated using the following equation.
where X(0) is the initial condition, the amount in the body at the time 0, and Ke the elimination rate constant.
Here e−Ket is called the impulse response function, or the response function to the unit impulse.
Eq. 1 is the solution to the following differential equation (Eq. 2).
If the drug is infused intravenously with the rate R (Eq. 3), the solution is Eq. 4.
Eq. 4 is also viewed as a homogenous solution + a particular solution because Eq. 2 is a homogenous differential equation and Eq. 3 is an inhomogeneous differential equation.
The followings are true in general.
where
A: coefficient matrix
→X(t)
: general solution of the differential equation
d→Xdt=A→X+→f(t)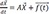
→XH(t)=exp(At)→Xo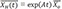
: solution of the homogenous differential equation
d→Xdt=A→X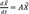
exp(At): impulse response function
→f(t)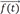
: input function
→XP(t)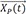
: particular solution of the inhomogeneous differential equation
*: convolution operator
If a drug is infused and administered orally, the differential equation is
where Ka is the absorption rate constant, and Xg(0) is the orally administered dose multiplied by its bioavailability.
Then the solution is
This is interestingly the summation of each solution for intravenous bolus, infusion, and oral dosing.
If Ka = Ke = K, the solution becomes
Go to :

Two-compartment model with non-zero initial condition
The differential equation for a typical two-compartment model is
where
Ke = K10: the elimination rate constant from the central compartment
Kcp = K12: the rate constant from the central to the peripheral compartment
Kpc = K21: the rate constant from the peripheral to the central compartment
R: infusion rate to the central compartment. Infusion is given to the central compartment only.
Ka: the absorption rate constant from the gut compartment
Xg(0): amount in the gut compartment at time 0. It is after the multiplication with bioavailability.
The solution of the above would be the following.
L−1 indicates inverse Laplace transformation.
For the matrix within the brackets,
is inverted to have
The denominator is a quadratic equation, and if the roots are −λ1 and −λ2,
where
Here, we present only the case that roots are two distinct real values, because this is practically true in real situation.
where
C1=λ1−Kpcλ1−λ2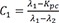 C2=Kpc−λ2λ1−λ2
C2=Kpc−λ2λ1−λ2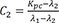 C3=−Kpcλ1−λ2
C3=−Kpcλ1−λ2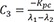 C4=Kpcλ1−λ2
C4=Kpcλ1−λ2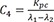
C5=−Kcpλ1−λ2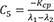 C6=Kcpλ1−λ2
C6=Kcpλ1−λ2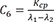 C7=λ1−Ke−Kcpλ1−λ2
C7=λ1−Ke−Kcpλ1−λ2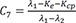 C8=Ke+Kcp−λ2λ1−λ2
C8=Ke+Kcp−λ2λ1−λ2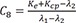
Therefore,
Therefore, the homogenous solution is
Then the particular solution for intravenous dosing is
Because the infusion rate for the peripheral compartment is zero, we can only consider the first column of exp(At).
If we integrate Eq. 25,
and
The particular solution for an oral dose is
Integration of Eq. 28 becomes
and
then
Now we can add Eq. 24, Eq. 27, and Eq. 31 for the general solution
For intravenous only or oral administration only, replace Xg(0) or R with 0 respectively.
Special cases, when one of the divisors is 0, have different solutions.
When Kpc = Kcp = λ2 = 0 (therefore λ1 = ke), the solution reduces to that of the one-compartment model.
Go to :

Three-compartment model with non-zero initial condition
The differential equation for a typical three-compartment model is
where
K10: the elimination rate constant from the central compartment
K12: the rate constant from the central to the first peripheral compartment
K21: the rate constant from the first peripheral to the central compartment
K13: the rate constant from the central to the second peripheral compartment
K31: the rate constant from the second peripheral to the central compartment
R: infusion rate to the central compartments. Infusion rates for the peripheral compartments are 0s.
Ka: the absorption rate constant from the gut compartment
Xg(0): amount in the gut compartment at time 0. It is after the multiplication with bioavailability.
The above equation can be solved with the same way to the two-compartment model case.
where
Let −λ1, −λ2, −λ3 be the three distinct roots of real values. (In real situations, roots are almost always three distinct real values.)
where
C1=(K21−λ1)(K31−λ1)(λ2−λ1)(λ3−λ1)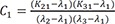 C2=(K21−λ2)(K31−λ2)(λ1−λ2)(λ3−λ2)
C2=(K21−λ2)(K31−λ2)(λ1−λ2)(λ3−λ2)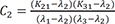 C3=(K21−λ3)(K31−λ3)(λ1−λ3)(λ2−λ3)
C3=(K21−λ3)(K31−λ3)(λ1−λ3)(λ2−λ3)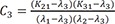
C4=K21(K31−λ1)(λ2−λ1)(λ3−λ1)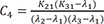 C5=K21(K31−λ2)(λ1−λ2)(λ3−λ2)
C5=K21(K31−λ2)(λ1−λ2)(λ3−λ2)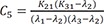 C6=K21(K31−λ3)(λ1−λ3)(λ2−λ3)
C6=K21(K31−λ3)(λ1−λ3)(λ2−λ3)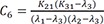
C7=K31(K21−λ1)(λ2−λ1)(λ3−λ1)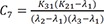 C8=K31(K21−λ2)(λ1−λ2)(λ3−λ2)
C8=K31(K21−λ2)(λ1−λ2)(λ3−λ2)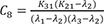 C9=K31(K21−λ3)(λ1−λ3)(λ2−λ3)
C9=K31(K21−λ3)(λ1−λ3)(λ2−λ3)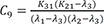
C10=K12(K31−λ1)(λ2−λ1)(λ3−λ1)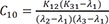 C11=K12(K31−λ2)(λ1−λ2)(λ3−λ2)
C11=K12(K31−λ2)(λ1−λ2)(λ3−λ2)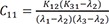 C12=K12(K31−λ3)(λ1−λ3)(λ2−λ3)
C12=K12(K31−λ3)(λ1−λ3)(λ2−λ3)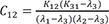
C16=K12K31(λ2−λ1)(λ3−λ1)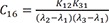 C17=K12K31(λ1−λ2)(λ3−λ2)
C17=K12K31(λ1−λ2)(λ3−λ2)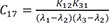 C18=K12K31(λ1−λ3)(λ2−λ3)
C18=K12K31(λ1−λ3)(λ2−λ3)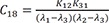
C19=K13(K21−λ1)(λ2−λ1)(λ3−λ1)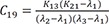 C20=K13(K21−λ2)(λ1−λ2)(λ3−λ2)
C20=K13(K21−λ2)(λ1−λ2)(λ3−λ2)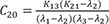 C21=K13(K21−λ3)(λ1−λ3)(λ2−λ3)
C21=K13(K21−λ3)(λ1−λ3)(λ2−λ3)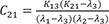
C22=K21K13(λ2−λ1)(λ3−λ1)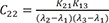 C23=K21K13(λ1−λ2)(λ3−λ2)
C23=K21K13(λ1−λ2)(λ3−λ2)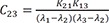 C24=K21K13(λ1−λ3)(λ2−λ3)
C24=K21K13(λ1−λ3)(λ2−λ3)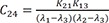
Heaviside cover-up method is convenient to get the above Cs.
Therefore, the impulse response function is
and the homogenous solution is
The particular solution for an intravenous infusion is
Similarly, the particular solution for an oral dose is
Consequently, the summation of Eq. 38, Eq. 39, and Eq. 40 is the general solution for the three-compartment model.
In cases of intravenous only or oral administration only, replace Xg(0) or R with 0 respectively.
When one of the divisors becomes 0, the solution is different from the above.
When K13 = K31 = λ3 = 0, the solution reduces to that of the two-compartment model.
Go to :

Conclusion
The analytical solutions of linear pharmacokinetic compartment models with a non-zero initial condition can be obtained elegantly using the matrix operations, integration, and the following facts
i) Pharmacokinetic compartment models for intravenous infusion or oral administration can be expressed using inhomogeneous differential equations.
ii) The general solution of an inhomogeneous differential equation is the sum of the homogenous solution and the particular solution.
iii) The particular solution is the convolution of the impulse response function from the homogenous solution and the input functions such as intravenous infusion rate or input rate from the depot compartment.
iv) Laplace transformation can be used to solve coupled linear differential equations.
Go to :

 : general solution of the differential equation d→Xdt=A→X+→f(t)
: general solution of the differential equation d→Xdt=A→X+→f(t)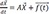
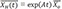 : solution of the homogenous differential equation d→Xdt=A→X
: solution of the homogenous differential equation d→Xdt=A→X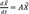
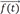 : input function
: input function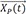 : particular solution of the inhomogeneous differential equation
: particular solution of the inhomogeneous differential equation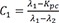 C2=Kpc−λ2λ1−λ2
C2=Kpc−λ2λ1−λ2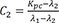 C3=−Kpcλ1−λ2
C3=−Kpcλ1−λ2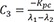 C4=Kpcλ1−λ2
C4=Kpcλ1−λ2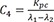
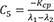 C6=Kcpλ1−λ2
C6=Kcpλ1−λ2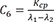 C7=λ1−Ke−Kcpλ1−λ2
C7=λ1−Ke−Kcpλ1−λ2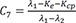 C8=Ke+Kcp−λ2λ1−λ2
C8=Ke+Kcp−λ2λ1−λ2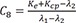
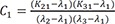 C2=(K21−λ2)(K31−λ2)(λ1−λ2)(λ3−λ2)
C2=(K21−λ2)(K31−λ2)(λ1−λ2)(λ3−λ2)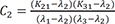 C3=(K21−λ3)(K31−λ3)(λ1−λ3)(λ2−λ3)
C3=(K21−λ3)(K31−λ3)(λ1−λ3)(λ2−λ3)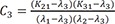
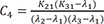 C5=K21(K31−λ2)(λ1−λ2)(λ3−λ2)
C5=K21(K31−λ2)(λ1−λ2)(λ3−λ2)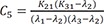 C6=K21(K31−λ3)(λ1−λ3)(λ2−λ3)
C6=K21(K31−λ3)(λ1−λ3)(λ2−λ3)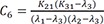
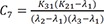 C8=K31(K21−λ2)(λ1−λ2)(λ3−λ2)
C8=K31(K21−λ2)(λ1−λ2)(λ3−λ2)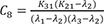 C9=K31(K21−λ3)(λ1−λ3)(λ2−λ3)
C9=K31(K21−λ3)(λ1−λ3)(λ2−λ3)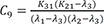
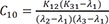 C11=K12(K31−λ2)(λ1−λ2)(λ3−λ2)
C11=K12(K31−λ2)(λ1−λ2)(λ3−λ2)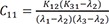 C12=K12(K31−λ3)(λ1−λ3)(λ2−λ3)
C12=K12(K31−λ3)(λ1−λ3)(λ2−λ3)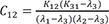
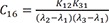 C17=K12K31(λ1−λ2)(λ3−λ2)
C17=K12K31(λ1−λ2)(λ3−λ2)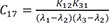 C18=K12K31(λ1−λ3)(λ2−λ3)
C18=K12K31(λ1−λ3)(λ2−λ3)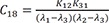
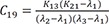 C20=K13(K21−λ2)(λ1−λ2)(λ3−λ2)
C20=K13(K21−λ2)(λ1−λ2)(λ3−λ2)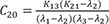 C21=K13(K21−λ3)(λ1−λ3)(λ2−λ3)
C21=K13(K21−λ3)(λ1−λ3)(λ2−λ3)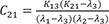
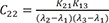 C23=K21K13(λ1−λ2)(λ3−λ2)
C23=K21K13(λ1−λ2)(λ3−λ2)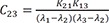 C24=K21K13(λ1−λ3)(λ2−λ3)
C24=K21K13(λ1−λ3)(λ2−λ3)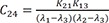




 PDF
PDF ePub
ePub Citation
Citation Print
Print



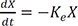
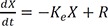
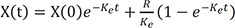
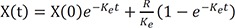
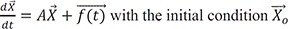
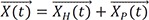
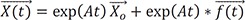
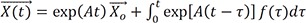
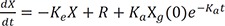
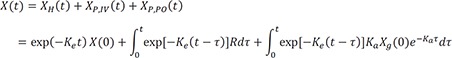
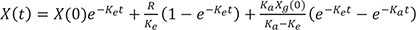
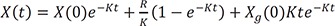
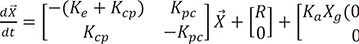
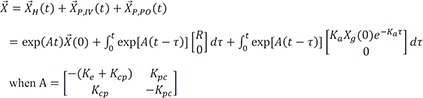
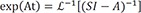
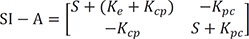
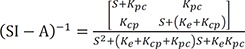
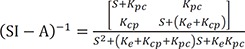
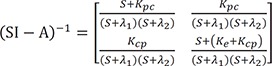
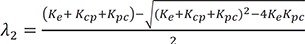
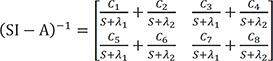
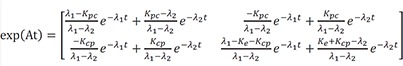
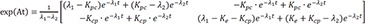
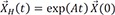
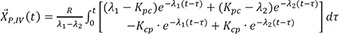
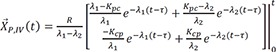
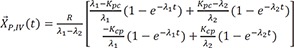
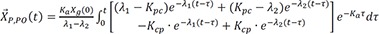
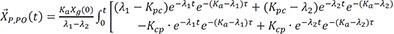
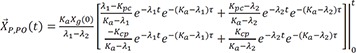
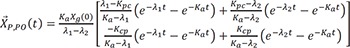
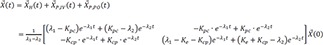
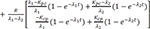
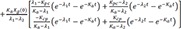
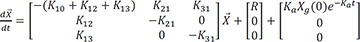
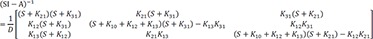
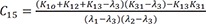
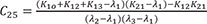
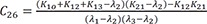
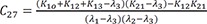
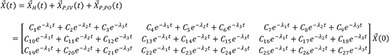
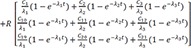
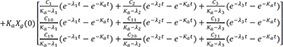
 XML Download
XML Download