PDF
ePub
Citation
Print
Abstract
The biomechanics study of the hip is aims to understand and explore the dynamic principles of weight transfer through the hip joint. This basic science knowledge can be applied in a variety of areas, including degenerative joint diseases and hip replacement arthroplasty. In particular, understanding of the biomechanics of the hip has led to the development of materials, design and fixation of implants, and it can be applied in various areas, such as the selection of surgical methods and the location of the implant. Moreover, it is essential to have good knowledge of the biomechanics of the hip to achieve better clinical results for patients. Therefore, this paper introduces the basic knowledge and biomechanical characteristics of a normal hip and hip replacement arthroplasty, which are needed to approach the biomechanics of the hip.
References
1. Houcke JV, Khanduja V, Pattyn C, Audenaert E. The history of biomechanics in total hip arthroplasty. Indian J Orthop. 2017. 51:359–67.
2. Mow VC, Ateshian GA, Spilker RL. Biomechanics of diarthrodial joints: a review of twenty years of progress. J Biomech Eng. 1993. 115:460–7.
3. Polkowski GG, Clohisy JC. Hip biomechanics. Sports Med Arthrosc Rev. 2010. 18:56–62.
4. Bombelli R. The biomechanics of the normal and dysplastic hip. Chir Organi Mov. 1997. 82:117–27.
5. Maquet P. Biomechanics of hip dysplasia. Acta Orthop Belg. 1999. 65:302–14.
6. McLeish RD, Charnley J. Abduction forces in the one-legged stance. J Biomech. 1970. 3:191–209.
7. Charnley J. Arthroplasty of the hip. A new operation. Lancet. 1961. 1:1129–32.
8. Lim LA, Carmichael SW, Cabanela ME. Biomechanics of total hip arthroplasty. Anat Rec. 1999. 257:110–6.
9. Carter DR, Hayes WC. The compressive behavior of bone as a two-phase porous structure. J Bone Joint Surg Am. 1977. 59:954–62.
10. Crowninshield RD, Pedersen DR, Brand RA. A measurement of proximal femur strain with total hip arthroplasty. J Biomech Eng. 1980. 102:230.
11. Engh CA, Bobyn JD, Glassman AH. Porous-coated hip replacement. The factors governing bone ingrowth, stress shielding, and clinical results. J Bone Joint Surg Br. 1987. 69:45–55.
12. Carter DR, Orr TE, Fyhrie DP. Relationships between loading history and femoral cancellous bone architecture. J Biomech. 1989. 22:231–44.
13. Prendergast PJ, Huiskes R. The biomechanics of Wolff’s law: recent advances. Ir J Med Sci. 1995. 164:152–4.
14. Sumner DR, Galante JO. Determinants of stress shielding: design versus materials versus interface. Clin Orthop Relat Res. 1992. 274:202–12.
15. Kutzner KP, Freitag T, Bieger R. . Biomechanics of a cemented short stem: standard vs. line-to-line cementation techniques. A biomechanical in-vitro study involving six osteoporotic pairs of human cadaver femurs. Clin Biomech (Bristol, Avon). 2018. 52:86–94.
16. Yettram AL, Wright KW. Biomechanics of the femoral component of total hip prostheses with particular reference to the stress in the bone-cement. J Biomed Eng. 1979. 1:281–5.
17. Jasty M, Burke D, Harris WH. Biomechanics of cemented and cementless prostheses. Chir Organi Mov. 1992. 77:349–58.
18. Bieger R, Ignatius A, Reichel H, Dürselen L. Biomechanics of a short stem: in vitro primary stability and stress shielding of a conservative cementless hip stem. J Orthop Res. 2013. 31:1180–6.
19. Bishop NE, Burton A, Maheson M, Morlock MM. Biomechanics of short hip endoprostheses—the risk of bone failure increases with decreasing implant size. Clin Biomech (Bristol, Avon). 2010. 25:666–74.
20. Morscher EW, Wirz D. Current state of cement fixation in THR. Acta Orthop Belg. 2002. 68:1–12.
21. Tanzer M, Maloney WJ, Jasty M, Harris WH. The progression of femoral cortical osteolysis in association with total hip arthroplasty without cement. J Bone Joint Surg Am. 1992. 74:404–10.
Figure 1.
Moment (M) is defined as the product of the force (F) and the vertical distance (I) at which it is applied (M=F×I).
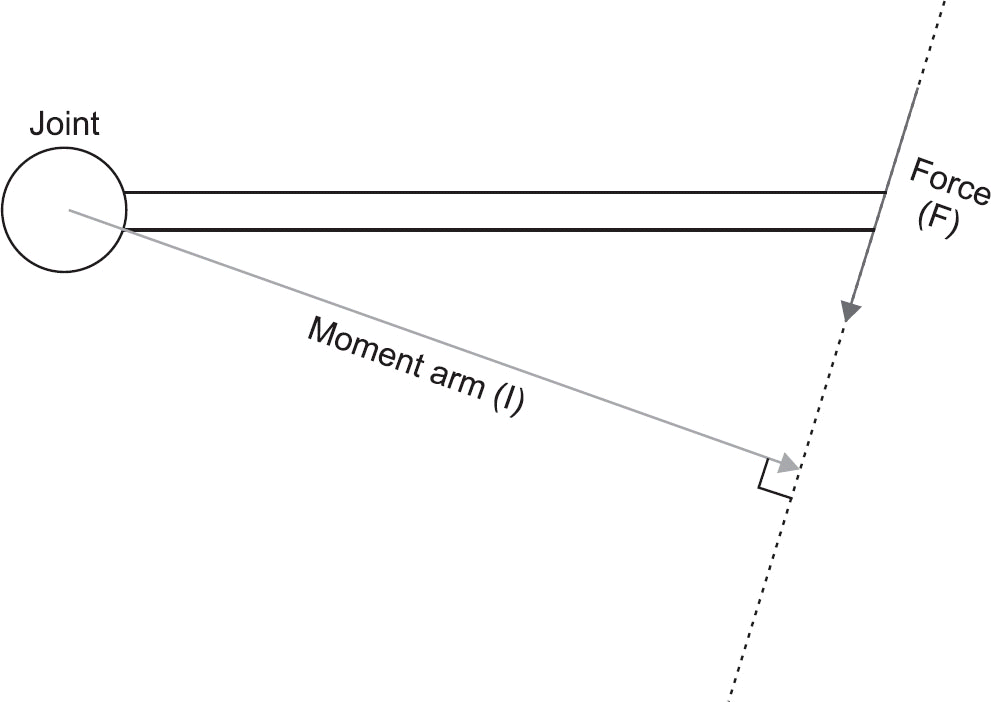
Figure 2.
According to the lever principle, the value of multiplying the abductor force (F) by the distance of the abductor moment arm (A) is equal to the value obtained by multiplying the weight (5/6W) by the distance of the weight arm (B).
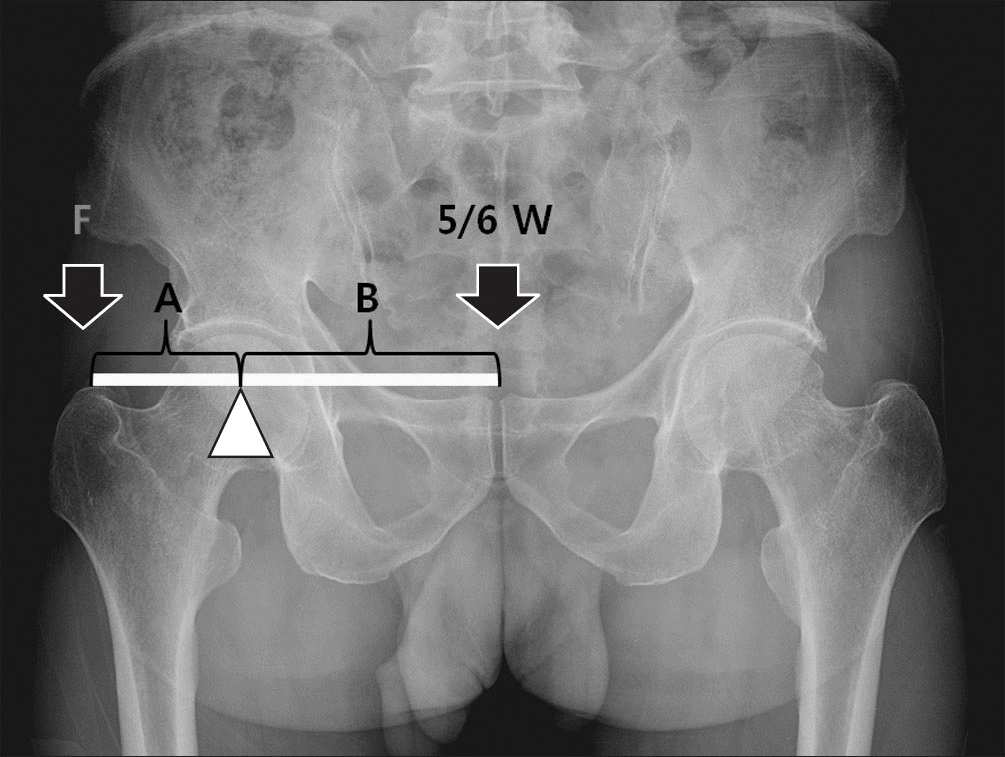
Figure 3.
The moment of body weight is equal to the sum of the moment of the abductor (F) and the cane (F’). A, moment arm of the abductor; B, moment arm of body center; C, distance between body center and cane; F’, the applied force to cane; W, weight.
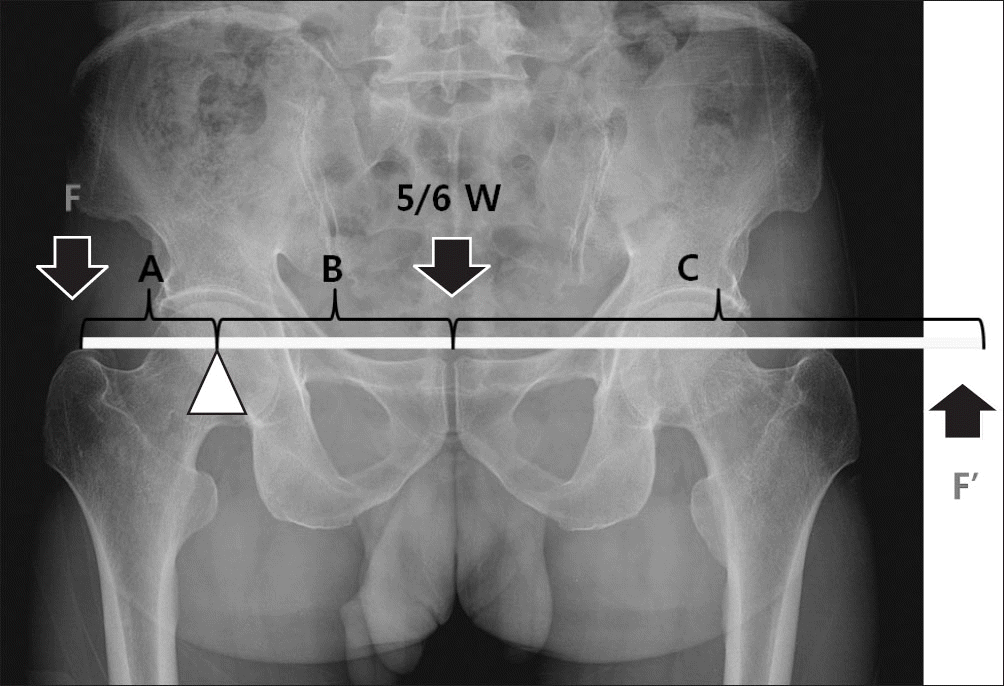
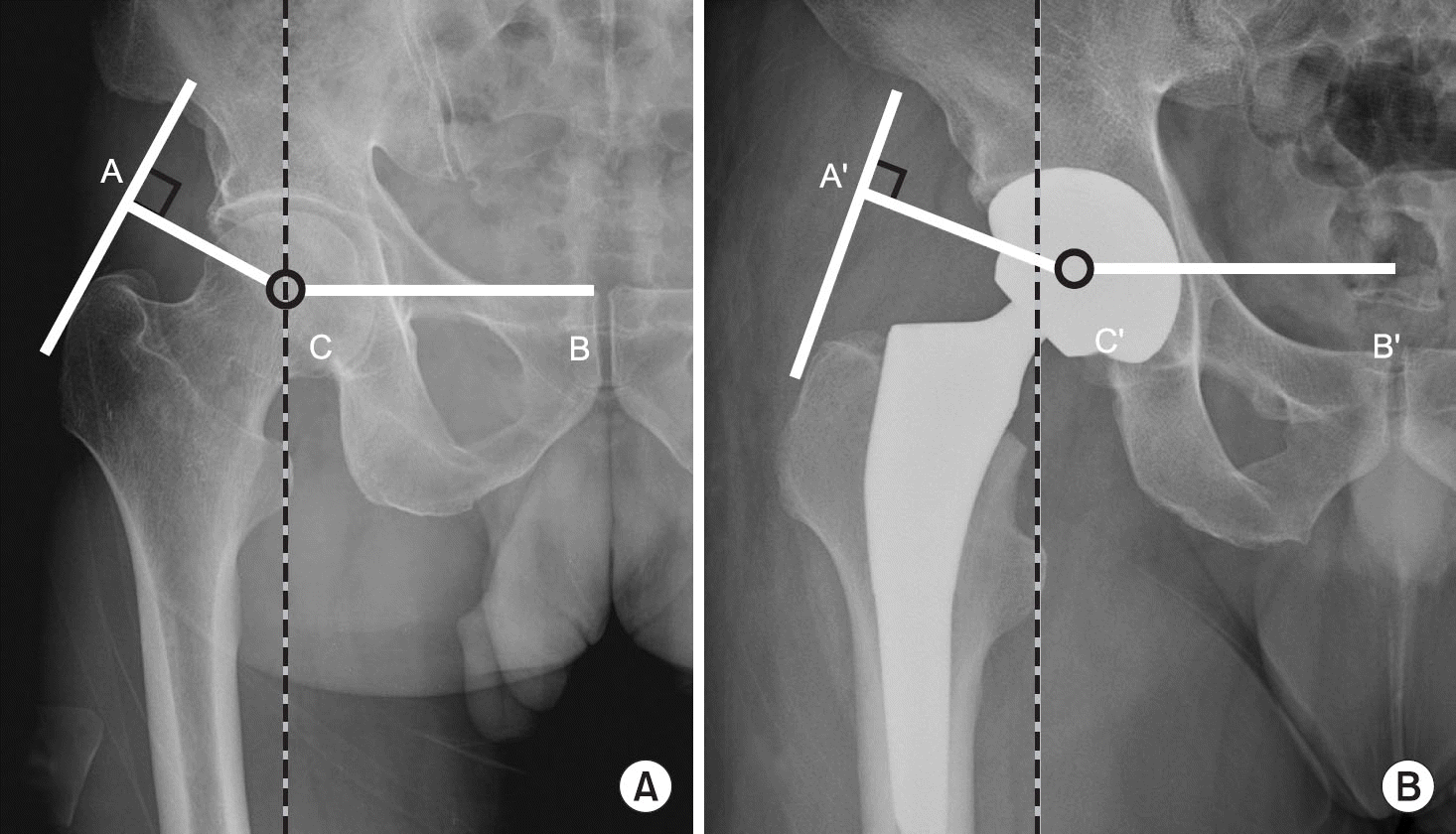
Figure 4.
X-ray images of before (A) and after (B) hip replacement arthroplasty. After hip replacement arthroplasty, the center of the hip was moved inside and the moment arm of the abductorwas extended. AC, moment arm of the abductor; BC, moment arm of body weight; C, center of the hip joint; A’C, moment arm of the abductor after hip replacement arthroplasty; B’C, moment arm of the body weight after hip replacement arthroplasty; C’, center of the hip after total hip arthroplasty.
XML Download