Toward a grey box approach for cardiovascular physiome

Minki Hwang; Chae Hun Leem; Eun Bo Shim

doi:10.4196/kjpp.2019.23.5.305

Journal List > Korean J Physiol Pharmacol > v.23(5) > 1130906

Go to TopGo to Top Go to BottomGo to Bottom

TOOLS

Hwang, Leem, and Shim: Toward a grey box approach for cardiovascular physiome

Review Article

The Korean Journal of Physiology & Pharmacology 2019; 23(5): 305-310.

Published online: 26 August 2019

DOI: https://doi.org/10.4196/kjpp.2019.23.5.305

Toward a grey box approach for cardiovascular physiome

Minki Hwang¹, Chae Hun Leem², Eun Bo Shim^1,³

¹SiliconSapiens Inc., Seoul 06097, Korea.

²Department of Physiology, University of Ulsan College of Medicine, Seoul 05505, Korea.

³Department of Mechanical and Biomedical Engineering, Kangwon National University, Chuncheon 24341, Korea.

Correspondence: Eun Bo Shim. ebshim@kangwon.ac.kr

Received 10 July 2019 Revised 2 August 2019 Accepted 6 August 2019

The Korean Physiological Society and The Korean Society of Pharmacology

(open-access):

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

The physiomic approach is now widely used in the diagnosis of cardiovascular diseases. There are two possible methods for cardiovascular physiome: the traditional mathematical model and the machine learning (ML) algorithm. ML is used in almost every area of society for various tasks formerly performed by humans. Specifically, various ML techniques in cardiovascular medicine are being developed and improved at unprecedented speed. The benefits of using ML for various tasks is that the inner working mechanism of the system does not need to be known, which can prove convenient in situations where determining the inner workings of the system can be difficult. The computation speed is also often higher than that of the traditional mathematical models. The limitations with ML are that it inherently leads to an approximation, and special care must be taken in cases where a high accuracy is required. Traditional mathematical models are, however, constructed based on underlying laws either proven or assumed. The results from the mathematical models are accurate as long as the model is. Combining the advantages of both the mathematical models and ML would increase both the accuracy and efficiency of the simulation for many problems. In this review, examples of cardiovascular physiome where approaches of mathematical modeling and ML can be combined are introduced.

Keywords: Machine learning, Mathematical model, Patient-specific modeling

INTRODUCTION

Since the birth of the modern concept of artificial intelligence (AI) in the 1950s [1], development has occurred in fits and starts; recently, with advances in computing hardware, AI is experiencing an unprecedentedly rapid progress and widespread adoption. Big data, which is indispensable in the application of AI, is now manageable by virtue of the increased computing power. Among the branches of AI, machine learning (ML) includes algorithms that can learn to predict outcomes given input data by means of training, which is a process of determining model parameters [2]. A set of ML algorithms utilizes artificial neural networks consisting of artificial neurons mimicking those of humans (Fig. 1A). The network consists of multiple layers composed of nodes at which values are computed based on the node values of the previous layer using the weights defined between each node of the adjacent layers (Fig. 1A). When the number of layers increases, the algorithm is called “deep learning” [3].

Traditionally, mathematical models were constructed to describe phenomena in nature or explain their mechanism, and predictions were made by solving model equations. This methodology is based on the notion that there are underlying laws for every phenomenon in nature. By contrast, the aforementioned AI approach does not consider any underlying laws, and can be applied to any phenomenon in nature or society even when constructing a mathematical model is difficult. Another benefit of using AI in prediction is that the computational speed is often higher than the mathematical model. Conversely, a drawback of the AI approach is that it is inherently an approximation, and special care is required in situations where high accuracy is needed. Combining the advantages of both mathematical model and AI approach would increase both accuracy and efficiency of the simulation for many problems.

Here, we review some of the examples in the area of cardiovascular physiome in which mathematical modeling and ML can be combined. Some of the popular ML techniques are explained first, and examples in the area of cardiovascular image processing, blood flow, cardiac electrical wave propagation, and drug toxicity analysis are introduced. We discuss combining mathematical models and ML approach to maximize the accuracy and efficiency of the simulations.

MACHINE LEARNING METHODOLOGIES

Artificial neural network

An artificial neural network (ANN) is a model of decisionmaking process, which uses artificial neurons mimicking those of humans. The decision is made based on the final values obtained from the computations defined by the structure of the network. The network consists of multiple layers composed of nodes (Fig. 1A). The value of each node is computed using the values of nodes in the preceding layer and the weights defined between each node. The following formula is typically used to compute the node values.

y_{j} = \sum_{i = 1}^{N} (w_{i j} \times x_{i}) + b_{j}

where y_j is the jth node value of the current layer, N is the number of nodes in the preceding layer, x_j is the ith node value of the preceding layer, w_ij is the weight specified between x_j and y_j, and b_j is the jth constant called ‘bias’. The values of w_ij and b_j can be obtained using various algorithms given a set of known input and output data. The process of obtaining w_ij and b_j is called ‘training’. Once training is completed, i.e., the values of w_ij and b_j are obtained, an output can be calculated for a new set of input data. Many software libraries provide w_ij and b_j for a given set of input and output data. The quality of the output is dependent on the number of layers and nodes, and these numbers need to be ascertained for a given problem.

Convolutional neural network

Convolutional neural networks (CNN) are mainly used in image analysis [4]. A set of weights, usually in the form of a 3 × 3 matrix, is shifted over the image pixels and multiplied with the pixel values to generate a new image (Fig. 1B). This new image contains the main features of the original one and is called the ‘feature map’. A large number of feature maps is usually generated, and after going through several layers, eventually converge to a single map or single value, which is the final prediction. The set of weights is called the ‘kernel’ or ‘filter’, and can be of any size such as 5 × 5 or 7 × 7. A CNN can be more efficient than an ANN because the number of weights can be much smaller (e.g., 9 in the case of a 3 × 3 filter). The values of the weights are obtained using various algorithms given a set of input images and known output data (training). There are software libraries available to determine the adequate weights as in the case of an ANN. When a new input is provided, for which the output is not known, a prediction is made using the obtained weights. The quality of the output is dependent on the number of feature maps, layers and kernel size, and these numbers need to be ascertained for a given problem.

Generative adversarial network

A generative adversarial network (GAN) is an unsupervised ML model which implies that training is performed without a known output [5 6]. A GAN is mainly used in image analysis to produce the images of certain features. Training is performed with two networks: a generator and a discriminator. A generator network produces an output image, and a discriminator network compares the output image to the real image. The training of the networks is performed in such a way that the discriminator quantifies the difference between the image generated by the generator and the real image, and the difference is minimized. ANNs or CNNs can be used for both the generator and discriminator networks.

APPLICATIONS OF MACHINE LEARNING TO PHYSIOMIC SIMULATIONS

Cardiovascular image processing

ML is increasingly used in cardiovascular image processing as it automates the process with greater accuracy [7 8 9 10]. It assists doctors in diagnosing and predicting diseases by accurately analyzing medical images. Increasingly sophisticated ML algorithms are being developed and applied in medical image analysis. The areas of application of ML in medical image analysis include image recognition, segmentation, registration, and reconstruction [11]. Bratt et al. [12] performed aortic flow quantification applying ML to the segmentation of the aortic valve. They designed an ML model to track the aortic valve borders using a neural network approach, and compared the results with manual segmentation in a validation cohort [12]. An extensive review can be found in [8 10 11]. This ML algorithm can be combined with a traditional mathematical method of image segmentation. Fig. 2 presents an example of coronary artery segmentation coupling ML with a traditional mathematical method. We developed this method for the construction of a patient-specific model of coronary arteries that can be used in the computational analysis of coronary hemodynamics. The outcome of the coupling method is better than that of the ML only method.

Blood flow simulation

A blood flow simulation requires blood vessel segmentation from medical images, and ML algorithm can improve its quality. In addition to the segmentation, the blood flow simulation itself can benefit from ML algorithms [13 14 15 16]. Itu et al. [17] developed an ML-based model for predicting the fractional flow reserve (FFR) in coronary arteries (Fig. 3). Their model predicted FFR along the centerline of the coronary tree, in contrast with invasively measured FFR. Their ML model was trained with data obtained by traditional mathematical modeling. They generated a total of 12,000 coronary arterial geometries with various parameters such as the stenosis location, lesion length, and branching angle. They solved Navier–Stokes equations for these geometries and used the resulting data as input and output sets for the training data for the ML model. When the new sets of patient-specific geometries were used as input data for the ML model, the output FFR results from the ML model were nearly identical to those from mathematical modeling. It only took seconds for the ML model to generate an FFR solution, which is a dramatic reduction of computation time compared with the several hours required for mathematical modeling. McKinley et al. [18] reproduced the perfusion maps of the brain using supervised ML techniques. They trained various ML models with various set and patch sizes to determine the effects of these parameters. The current challenge in applying ML in the blood flow simulation is the prediction of long-term behavior as the error accumulates at each time step.

Cardiac electrical wave propagation

The electrical wave propagation in the heart is another active research area where computer simulation plays a significant role. In the mathematical modeling approach, the governing equation of the electrical wave propagation is solved numerically to obtain the electrical potential distribution in the heart as a function of time. A limitation of this approach is that the computation time would be prohibitive for application in clinical settings. ML can be an alternative as the computation time is reduced significantly. Cantwell et al. [19] observed that the computation time for solving a two-dimensional diffusion equation can be reduced by a factor of 40 using a fully convolutional neural network even in the absence of a cellular electrophysiology model in the equation. We attempted to use ML techniques to obtain solutions to the two-dimensional diffusion equation with a cellular electrophysiology model. Fig. 4 shows the electrical wave propagation during 150 ms from an initial distribution of membrane potential. The results from the ML model are compared with those from the mathematical model solutions. The ML model used was an artificial neural network with three hidden layers. The number of nodes for each hidden layer was 64, 16, and 4. The simulation results from the mathematical modeling were used for the training data for the ML model. The input training data was the voltage at a node and the eight surrounding nodes at the previous time step, and the output training data was the voltage at the node at the current time step. A time step size of 0.5 ms was used for the ML model. The computation time for the ML model was reduced by a factor of thirty approximately compared to mathematical modeling. Another area of cardiac electrophysiology where ML is actively used is electrocardiogram (ECG) analysis. ECG morphology is automatically analyzed and classified into a specific type of arrhythmia. A review of various techniques and clinical implications can be found in [20].

Drug toxicity analysis

ML can be utilized in all stages of drug development from target validation to data analysis in clinical trials [21]. In particular, the effect of drugs on the prolongation of the QT interval in ECG is of interest as the QT interval prolongation is a risk factor for the Torsade de Pointes which can lead to a sudden cardiac death. Constructing a mathematical model of the heart and torso that provides ECG given the changes in ionic currents is one way of testing the effects of drugs on the QT interval. Leveraging ML can be a faster way to accomplish the same task. Costabal et al. [22] constructed an ML model for testing the effect of drugs on the QT interval (Fig. 5). They built a surrogate model for the QT interval using a Gaussian process regression combining information from the mathematical modeling. They performed a sensitivity analysis to determine the effect of each individual ionic current on the QT interval. A review of the applications of ML in drug development can be found in [21].

GREY BOX APPROACH

When a model is needed for the prediction of the future behavior of a system, the traditional approach is to derive mathematical equations reflecting the workings of the system. This approach may be called ‘white box’ because the inner workings of the model are clearly described in the model equations (Fig. 6). By contrast, the ML approach is often labeled ‘black box’ as the model parameters are determined independently from the underlying mechanisms supporting the system (Fig. 6). The advantage of the ‘white box’ approach is that the inner workings of the system are accurately reflected in the model equation, but the drawback is that the mechanisms should be known a priori to build the model equations, and the computational time is often prohibitive. The ‘black box’ approach, in contrast, does not require the system mechanisms to be known a priori, and as a result, it can be applied to any system even when the mechanisms are unknown. The ‘black box’ approach is generally faster than the ‘white box’ when performing simulations even though the accuracy is generally inferior to that of the ‘white box’.

Considering their benefits and drawbacks in the methodological aspect, an alternative method in cardiovascular physiome can be to combine these two approaches and only retain the strengths of each approach. Deist et al. [23] recently reported a simulationassisted ML where they used approximate simulations in ML. Utilizing simulation results as training data in ML would be another example of ‘grey box’ approach. This approach looks promising and more efforts are probably needed in this direction. In a grey box approach, there exist two distinct versions: black box oriented and white box oriented (Fig. 6).

CONCLUSION

ML techniques are increasingly gaining adoption in almost every area of industry and academia, and new methods are constantly being developed by numerous experts. Physiomic simulation is also an area where the role of ML is rapidly increasing. The ‘black box’ approach, however, comes with benefits and limitations, as does the traditional ‘white box’ approach. Combining the two methodologies by only retaining the strength of each approach appears promising for maximizing the accuracy and efficiency of the predictions.

Figures and Tables

Fig. 1

Schematic machine learning (ML) algorithm.

A set of the ML algorithms utilizing artificial neural network consisting of artificial neurons mimicking those of human (A), and convolutional neural network mainly used in image analysis (B).

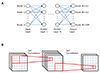
Fig. 2

An example of image segmentation method coupling machine learning (ML) and mathematical segmentation algorithm.

Here, there-dimensional model of coronary arteries was extracted from computed tomographic images.

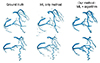
Fig. 3

Comparison of the fractional flow reserve (FFR) contours of coronary arteries.

(A) is computational fluid dynamics-based computed FFR distributions, and machine learning-based FFR distribution is shown in (B) (Figure from Itu L, et al. J Appl Physiol 2016;121:42-52 with permission [17]).

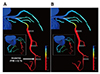
Fig. 4

Comparison of electric potential contours in two-dimensional cardiac tissue.

Upper panel is computed from a mathematical model. Lower panel was obtained from machine learning algorithm. Colors in the images represent electric potential level of cardiac tissue.

Fig. 5

A machine leanring model for testing the effect of drugs on the QT interval.

A surrogate model was built for the QT interval using a Gaussian process regression combining information from the mathematical modeling (Figure from Costabal FS, et al. Comput Methods Appl Mech Eng 2019;348:313–333 [22] [https://doi.org/10.1016/j.cma.2019.01.033] under the Creative Commons Attribution License [https://creativecommons.org/licenses/by/4.0/]).

Fig. 6

Schematic of grey box approach.

Grey box approach combines white box and black box approaches and only retains the strengths of each approach. AI, artificial intelligence.

ACKNOWLEDGEMENTS

We would like to thank Editage (www.editage.co.kr) for English language editing.

Notes

^{Author contributions} M.H. wrote the original draft. C.H.L. and E.B.S. edited the manuscript.

^{CONFLICTS OF INTEREST} The authors declare no conflicts of interest.

References

1. Russell SJ, Norvig P. Artificial intelligence: a modern approach. 2nd ed. New Delhi: Prentice Hall;2003.

2. Mitchell TM. Machine learning. New York: McGraw-Hill;1997.

3. Schmidhuber J. Deep learning in neural networks: an overview. Neural Netw. 2015; 61:85–117.

4. Krizhevsky A, Sutskever I, Hinton GE. Pereira F, Burges CJC, Bottou L, Weinberger KQ. ImageNet classification with deep convolutional neural networks. In : NIPS'12 Proceedings of the 25th International Conference on neural information processing systems; New York: Curran Associates Inc;2012. p. 1097–1105.

5. Goodfellow IJ, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, Courville A, Bengio Y. In : Ghahramani Z, Welling M, Cortes C, Lawrence ND, Weinberger KQ, editors. Generative adversarial nets. NIPS'14 Proceedings of the 27th International Conference on neural information processing systems; Cambridge: MIT Press Cambridge;2014. p. 2672–2680.

6. Ghahramani Z. Unsupervised learning. In : Bousquet O, von Luxburg U, Ratsch G, editors. Advanced lectures on machine learning. Berlin: New York: Springer;2004.

7. Lundervold AS, Lundervold A. An overview of deep learning in medical imaging focusing on MRI. Z Med Phys. 2019; 29:102–127.

8. Ker J, Wang L, Rao J, Lim T. Deep learning applications in medical image analysis. IEEE Access. 2017; 6:9375–9389.

9. Liu S, Wang Y, Yang X, Lei B, Liu L, Li S, Ni D, Wang T. Deep learning in medical ultrasound analysis: a review. Engineering. 2019; 5:261–275.

10. Shen D, Wu G, Suk HI. Deep learning in medical image analysis. Annu Rev Biomed Eng. 2017; 19:221–248.

11. Maier A, Syben C, Lasser T, Riess C. A gentle introduction to deep learning in medical image processing. Z Med Phys. 2019; 29:86–101.

12. Bratt A, Kim J, Pollie M, Beecy AN, Tehrani NH, Codella N, Perez-Johnston R, Palumbo MC, Alakbarli J, Colizza W, Drexler IR, Azevedo CF, Kim RJ, Devereux RB, Weinsaft JW. Machine learning derived segmentation of phase velocity encoded cardiovascular magnetic resonance for fully automated aortic flow quantification. J Cardiovasc Magn Reson. 2019; 21:1.

13. Kurata A, Fukuyama N, Hirai K, Kawaguchi N, Tanabe Y, Okayama H, Shigemi S, Watanabe K, Uetani T, Ikeda S, Inaba S, Kido T, Itoh T, Mochizuki T. On-site computed tomography-derived fractional flow reserve using a machine-learning algorithm- clinical effectiveness in a retrospective multicenter cohort. Circ J. 2019; 83:1563–1571.

14. Wang Z. Support vector machine learning-based cerebral blood flow quantification for arterial spin labeling MRI. Hum Brain Mapp. 2014; 35:2869–2875.

15. Jordanski M, Radovic M, Milosevic Z, Filipovic N, Obradovic Z. Machine learning approach for predicting wall shear distribution for abdominal aortic aneurysm and carotid bifurcation models. IEEE J Biomed Health Inform. 2018; 22:537–544.

16. Riordon J, Sovilj D, Sanner S, Sinton D, Young EWK. Deep learning with microfluidics for biotechnology. Trends Biotechnol. 2019; 37:310–324.

17. Itu L, Rapaka S, Passerini T, Georgescu B, Schwemmer C, Schoebinger M, Flohr T, Sharma P, Comaniciu D. A machine-learning approach for computation of fractional flow reserve from coronary computed tomography. J Appl Physiol (1985). 2016; 121:42–52.

18. McKinley R, Hung F, Wiest R, Liebeskind DS, Scalzo F. A machine learning approach to perfusion imaging with dynamic susceptibility contrast MR. Front Neurol. 2018; 9:717.

19. Cantwell CD, Mohamied Y, Tzortzis KN, Garasto S, Houston C, Chowdhury RA, Ng FS, Bharath AA, Peters NS. Rethinking multiscale cardiac electrophysiology with machine learning and predictive modelling. Comput Biol Med. 2019; 104:339–351.

20. Lyon A, Mincholé A, Martínez JP, Laguna P, Rodriguez B. Computational techniques for ECG analysis and interpretation in light of their contribution to medical advances. J R Soc Interface. 2018; 15:20170821.

21. Vamathevan J, Clark D, Czodrowski P, Dunham I, Ferran E, Lee G, Li B, Madabhushi A, Shah P, Spitzer M, Zhao S. Applications of machine learning in drug discovery and development. Nat Rev Drug Discov. 2019; 18:463–477.

22. Costabal FS, Matsuno K, Yao J, Perdikaris P, Kuhl E. Machine learning in drug development: characterizing the effect of 30 drugs on the QT interval using Gaussian process regression, sensitivity analysis, and uncertainty quantification. Comput Methods Appl Mech Eng. 2019; 348:313–333.

23. Deist TM, Patti A, Wang Z, Krane D, Sorenson T, Craft D. Simulation assisted machine learning. Bioinformatics. 2019; DOI: 10.1093/bioinformatics/btz199. [Epub ahead of print].

TOOLS

Similar articles