Deep Learning in MR Image Processing

Doohee Lee; Jingu Lee; Jingyu Ko; Jaeyeon Yoon; Kanghyun Ryu; Yoonho Nam

doi:10.13104/imri.2019.23.2.81

Journal List > Investig Magn Reson Imaging > v.23(2) > 1129699

Go to TopGo to Top Go to BottomGo to Bottom

TOOLS

Lee, Lee, Ko, Yoon, Ryu, and Nam: Deep Learning in MR Image Processing

Review Article

Investigative Magnetic Resonance Imaging 2019; 23(2): 81-99.

Published online: 30 June 2019

DOI: https://doi.org/10.13104/imri.2019.23.2.81

Deep Learning in MR Image Processing

Doohee Lee¹, Jingu Lee¹, Jingyu Ko¹, Jaeyeon Yoon¹, Kanghyun Ryu², Yoonho Nam³

¹Laboratory for Imaging Science and Technology, Department of Electrical and Computer Engineering, Institute of Engineering Research, Seoul National University, Seoul, Korea.

²Department of Electrical and Electronic Engineering, Yonsei University, Seoul, Korea.

³Department of Radiology, Seoul St. Mary's Hospital, College of Medicine, The Catholic University of Korea, Seoul, Korea.

Correspondence to: Yoonho Nam, Ph.D. Department of Radiology, Seoul St. Mary's Hospital, College of Medicine, The Catholic University of Korea, 222 Banpo-daero, Seocho-gu, Seoul 06591, Korea. Tel. +82-2-2258-1965, Fax. +82-2-599-6771, yhnam83@gmail.com

Received 12 September 2018 Revised 21 January 2019 Accepted 18 February 2019

Korean Society of Magnetic Resonance in Medicine

(open-access):

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

Recently, deep learning methods have shown great potential in various tasks that involve handling large amounts of digital data. In the field of MR imaging research, deep learning methods are also rapidly being applied in a wide range of areas to complement or replace traditional model-based methods. Deep learning methods have shown remarkable improvements in several MR image processing areas such as image reconstruction, image quality improvement, parameter mapping, image contrast conversion, and image segmentation. With the current rapid development of deep learning technologies, the importance of the role of deep learning in MR imaging research appears to be growing. In this article, we introduce the basic concepts of deep learning and review recent studies on various MR image processing applications.

Keywords: Deep learning, Machine learning, Image processing

INTRODUCTION

Recently, deep learning methods have shown great potential in various tasks that involve handling large amounts of digital data, including image (1), voice (2), and text data (3). In particular, image processing and computer vision applications employing deep learning have achieved remarkable success in applications including the denoising (4 5 6), recognition (1 7 8), detection, and segmentation (9 10) of objects. In the field of MR imaging research, deep learning methods are also being increasingly applied in a wide range of areas to complement or replace traditional model-based methods. Although most studies on these methods have been conducted and evaluated in a limited condition so as to show their general applicability, deep learning methods have shown remarkable improvements in several MR image processing areas, such as image reconstruction from under-sampled k-space data, image quality improvement, and organ or lesion segmentation from MR images. With the rapid developments currently underway in deep learning, data management, and computing technologies, the role of deep learning in MR imaging research appears to be increasingly important. In this article, we provide an overview of deep learning applications in MR image processing. First, we briefly introduce the basic concepts of deep learning. Second, we review recent studies on various MR image processing applications. Third, we introduce popular tools for deep learning implementation. Finally, we conclude with limitations and future directions of deep learning in MR image processing.

Deep Learning: a Brief Overview

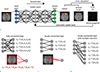
Deep learning is a branch of machine learning based on the use of multiple layers to learn data representations, and can be applied to both supervised and unsupervised learning (11). These multiple layers allow the machine to learn multiple level features of data in order to achieve its desired function. Figure 1a presents a simplified version of a neural network, which has been the most widely used deep learning architecture over the last decade. Each layer of deep learning architecture consists of a set of nodes, and each node is represented by a digitized number. For example, a set of voxels in image data is often used as an input layer in MR image processing applications. Typically, the nodes of the previous layer are connected to the nodes of the next layer through the weighted sum with bias. In addition, a non-linear activation function, such as a rectified linear unit or a hyperbolic tangent, is applied to the calculated values. With appropriate selection of the activation function, this activation process adds non-linearity to the network and accelerates the learning process (12). The nodes of the previous layer can be connected to each node of the next layer either fully or locally, as shown in Figure 1b and c, respectively. A locally-connected layer often has multiple channels. Figure 1d shows a locally-connected layer with two different channels. In this case, individual channels have their own connections. A representative example of such a layer is a convolutional layer with multiple convolution kernels. For image data, these are related to the size of the receptive field. This connection has adjustable parameters for weight (w) and bias (b), and the number of parameters depends on the number of connected nodes as well as the parameter-sharing method. The fully-connected layer can have a very large number of parameters to be optimized, because all of the nodes are connected with their weights and biases. By contrast, the convolutional layer (which is most widely used as a locally-connected layer based on single- or multi-dimensional convolution operations in image processing applications) has a relatively small number of parameters, because this layer shares the parameters for the convolution kernels. In the case of the convolutional layer, the number of parameters is mainly determined by the number of channels. In particular, the deep learning architecture that contains multiple convolutional layers to learn data representation is called the convolutional neural network (CNN). For image processing applications, CNN is one of the most popular and effective deep learning methods used (11). The deep learning training process automatically sets the values of the parameters of each layer so as to generate the output data we seek from the input data. The backpropagation procedure is typically used to determine the parameters of the multiple layers of the neural network (13 14). This procedure involves computing the gradients of the pre-determined objective functions with respect to the parameters, then updating the parameters based on these calculated gradients. For supervised learning with image processing applications, various error metrics (e.g., mean absolute error, mean squared error, and structural similarity) between the output and the ground truth can be used for the objective function. The overall training process can be summarized in the following six steps: 1. Initialize parameters (w, b), 2. Forward pass (Input → Output), 3. Error calculation (Output, Ground truth → E), 4. Backpropagation, 5. Update parameters (w, b), 6. Repeat steps 2-5 until E reaches an acceptable level. In this article, we briefly covered only a few important elements of the deep neural network, which is one of the representative architectures of deep learning. For further detail on the various deep learning architectures, refer to the previous studies (15 16) focusing on deep learning architectures.

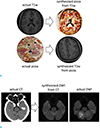
Based on the recent improvements in computational power and the large amount of curated data available, recent deep learning architectures can have very large numbers of layers and parameters. For example, GoogLeNet (17) has 22 layers with five million parameters and ResNet (7) has 152 layers with 60 million parameters. However, with these very high representational capacities, deep learning methods can suffer from the overfitting of results for insufficient training data. In addition, recent deep learning-based image processing methods have exhibited the ability to generate realistic fake images in various applications (18 19). In medical image processing, this possibility should be carefully considered. Figure 2a shows these high representational capacities of deep learning methods. Using a cycle-consistent adversarial network (20) and thousands of MR and pizza images, we trained the network to generate either pizza images from T1-weighted MR images or T1-weighted MR images from pizza images. Interestingly, the network showed the ability to learn a relationship between two datasets that initially appeared to be physically unrelated. Similarly, we trained the network to generate MR diffusion-weighted images from actual CT images using the co-registered actual CT and diffusion-weighted images. As shown in Figure 2b, the network generated the realistic synthesized diffusion-weighted image from the actual CT image. However, this generated diffusion-weighted image does not include the pathologic information which appears on the corresponding actual diffusion-weighted image. Note that this example is a simple experiment meant to demonstrate the ability of deep learning to generate a realistic fake image. This example does not demonstrate that deep learning cannot accomplish this task. Practically, it is very difficult to show the reliability of the information of the image generated by deep learning from the limited test data, but this is much more important than generating a realistic image in the field of medical image processing. When developing a deep learning-based method, using a rigorous evaluation process is essential to avoid overfitting to training data or the generation of fake information. In order to evaluate the performance of the network, it is generally recommended to split data into training, valid, and test sets. The training set data are used to determine the network parameters. In most cases, the network shows good performance for the training set after an iterative learning process with the proper adjustment of the network structure and its hyperparameters, due to its very high capacity. Therefore, the separate validation set is required to predict the general performance of the network. The data in the validation set should not be fed into the network because the model should have the ability to apply external data not included in the training process. The network structure and its hyperparameters are typically adjusted by monitoring the performance of the network for the validation set. Eventually, the network was tuned to show good performances for both the training and validation sets. However, this still did not guarantee good performance for data not in the training and validation sets. For this reason, the test data set is also required, and should only be used to evaluate the performance of a completely trained network. If the training and validation sets show good results but the test set does not show good results, the network is considered to be overfitted. The optimally fitted network shows good or similar performances for all three data sets. Figure 3 summarizes data splitting for development and evaluation. In most MRI applications, it is difficult to collect sufficiently large amounts of training data to reflect the real world. Therefore, a researcher who wants to apply deep learning methods to MRI applications should carefully determine what data to collect, how much data to collect, and how to split the data.

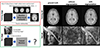
For the training set, data augmentation is generally recommended in order to increase the robustness for input data variances. Like other image processing applications, various spatial transformations including rotating, flipping, shifting, and resizing in the image domain as well as adding randomly generated noises with proper probability distributions are commonly used to augment input data. Figure 4 shows a simple example of the effect of data augmentation on deep learning. We trained the deep neural network using 27 T1-weighted MR images as outputs and the corresponding Fourier domain data (k-space in MR) as inputs from a single subject in order to investigate whether the neural network could learn the 2D Fourier transform for general images. The networks without and with data augmentation were trained using MR data from a single subject and tested using the Fourier domain data of another MR image and a “Lena” image. Excluding augmentation, all parameters, such as learning rate and epoch, were the same across the two networks. In this example, the slightly modified architecture of automated transform by manifold approximation (21) was used for training and testing. Image rotating, flipping, and shifting, as well as the addition of Gaussian random noises were used for data augmentation. For both networks, the representative image of the training set shows similar reconstruction results. By contrast, the “Lena” image shows largely different reconstruction results for the two networks. Through the use of data augmentation, this network has learned 2D Fourier transform for general images to some extent. Although this simple example shows the potential of successful learning by using conventional data augmentation due to the explicit relationship between the input and output data, the characteristics of MR imaging should be considered when performing data augmentation in practical MR image processing applications. For example, the spatial sensitivities of the individual receive coils and the reconstruction methods for accelerated data are closely related to the noise patterns appearing on MR images. These noise patterns of MR images differ from those of natural images or other medical imaging devices. Physiological motions of a subject during data acquisition can also highly affect the noise patterns on MR images. Therefore, understanding the MR physics and data acquisition process is helpful for appropriate data augmentation in most MR image processing applications. In some cases, simulated data based on MR physics can be used to increase the diversity of training data. For example, parameter mapping from MR images is generally conducted through model fitting from the acquired MR images. Based on the model, infinite simulated signals can theoretically be generated and used for the training set. It would be effective to use an appropriate model to represent the MR data. However, it is still difficult in practice to solve most MR image processing problems in this way, due to various factors that are not included in the model.

MR Image Processing Applications

Image Reconstruction

Brief History of MR Image Reconstruction

The concept of reconstructing images from nuclear magnetic resonance signals was developed using the spatial encoding capability of field gradient coils (22 23). The encoding scheme first applies a spatially varying magnetic field, a so-called gradient field, in order to allocate a certain nuclear resonance frequency for a location. Then, each location of the signal is inversely speculated from the encoded frequency spectrum. In this process, we call the encoded signals in the spatial frequency domain ‘k-space’. MRI reconstruction involves how to transform k-space into image domain. In the early history of MRI, the most basic and important link between the two domains was the Fourier transformation relationship. The Fourier transformation between the domains is based on one-to-one matching, and thus the total number of k-space data points required to generate the image array is the same as the number of image array elements, in conventional MRI reconstruction.

Further spatial encoding possibility by using multi-coil data acquisition has been shown to lead to a substantially faster data acquisition time. Since the data of each channel are acquired simultaneously and have independent spatial sensitivity information, we can reduce the frequency encoding steps (i.e., decreasing k-space sampling rates). This type of fast data acquisition and subsequent reconstruction is referred to as ‘parallel imaging’. For the reconstruction, the sensitivity maps of individual coils were used to differentiate aliased images due to the reduced sampling rate in k-space (24 25 26). Parallel imaging has revolutionized MRI from two perspectives: First, it demonstrated the potential to go beyond Nyquist sampling theorem using additional information. Secondly, it improved the clinical usefulness of MRI by reducing the scan time.

Beyond the gradient field and multi-coil encodings, morphological priors for the reconstructed images have been utilized to innovate MRI reconstruction performance. One milestone study suggested that the wavelet transform of the natural images should be sparse, inspired by the JPEG2000 compression standard (27). Under this assumption, rarely-sampled k-space data can be reconstructed to ground-truth images by removing noisy artifacts. Unlike the multi-coil acceleration scheme, the procedure includes the concept of non-linear transformation, which may result in an improved signal-to-noise ratio. However, it also involves the risk of concealing image details beneath the morphological constraints.

Deep Learning for MR Image Reconstruction

A deep neural network has been used to imitate the conventional image reconstruction methods. The reasons for why deep learning is intensively tested for reconstruction fall into the following three categories: 1) to learn data-driven prior, 2) to take advantage of high reconstruction speed, and 3) to improve and optimize the conventional reconstruction methods. In this section, we review how the deep learning method can cause differences in the categories as compared to the conventional reconstruction (Fig. 5).

Deep learning for the reconstruction mostly relies on data distribution to learn a function that maps input to output. Identifying weights and biases in a neural network involves fitting parameters that best describe the data distribution. Therefore, we refer to deep learning as a data-driven approach. From the property, the neural network memorizes image features and regards these as the prior condition (i.e., most probable solution), which is ambiguous to be planted in the physics model (1 28). This causes deep learning results to have seemingly nice quality and be robust to artifacts. On the other hand, their data-driven nature may become a drawback when the network is applied to data that was not involved in the training stage.

Without a doubt, the most time-consuming process in iterative reconstructions for accelerated MR data reconstruction is calculating the gradient of the object function with respect to the variables (29). In the deep learning approach, it is not necessary to calculate the gradient for the forwarding step; the gradient calculation is only done for the back propagation step in network training. Additionally, the number of deep learning parameters is designed to be much smaller than the number describing an arbitrary mapping from images to images. This dimension reduction can be attributed to the rationale of manifold approximation. A recent study demonstrated the manifold property of human brain images and proposed a neural network that transforms arbitrarily encoded k-space into images (21). This manifold approximation was additionally validated in other studies (30). Another group proposed a concept of residual labeling to facilitate manifold learning and explained the principles of manifold learning in a theoretical manner (31 32).

Another important application of deep learning is the optimization of nonlinear reconstruction. The recent state-of-the-art algorithm of the accelerated data reconstruction uses a featured domain to formulate the image prior as an optimization target function. For example, most compressed sensing reconstructions enforce the sparsity of the wavelet coefficients (i.e., minimizing the L1-norm of the wavelet transform of images). However, it is difficult to determine which domain or norm criteria shows the most optimal performance. Hammernik et al. (33) proposed manipulating the neural network structure to follow the compressed sensing reconstruction procedure. The network, named the ‘variational network’, allocates the activation functions and convolution kernels to be trained, making it so that we can find the best domain for sparsity enhancement and norm criteria for the reconstruction. The results outperform the conventional reconstruction methods and show good generalization potentials (34). As another example, Akcakaya et al. (35) suggested a neural network which replaces a linear k-space convolution kernel for parallel imaging reconstruction. In the image domain, several studies have formulated the same problem as de-aliasing tasks and used generative adversarial networks as well as conventional CNN to remove aliasing artifacts (36 37 38 39). In addition, a method that solves the parallel imaging problem in both k-space and image domains was proposed (40).

Further investigation is required to integrate the benefits of the deep learning and model-based approaches. A simple solution involves including model-based loss at the training phase of deep learning while the reconstruction time increases when using the customized loss function. Otherwise, one can merge deep learning-based loss to the optimization regularization terms (33 41). Another solution may be cascading model-based optimization and deep learning solution. These opportunities need to be investigated further in order to take full advantage of deep learning in addition to model knowledge.

Image Quality Improvement

Deep learning has become a promising technology that has been pushing the boundary of image quality enhancement. In natural image processing applications, deep learning-based methods for quality improvement are developing very rapidly (42). In recent MR image applications, the methods used for natural images have been adequately modified to apply MR images by considering the principles in which MRI images are generated, although early studies have been conducted by applying the methods originating from the field of natural image processing without modifications. In this section, we review recent deep learning studies on MR image denoising, artifact correction, super-resolution, and other quality enhancement methods.

Denoising is one of the most important aspects of image quality improvement. In practice, generally, the MR signals are always perturbed by various unwanted noises, and image denoising can be considered as an inverse problem of finding the values of the signal minimizing noise contaminations. The conventional image denoising methods are model-based methods, followed by sparse coding, effective prior, and low-rank approaches (43 44 45 46). Combined with the knowledge of the conventional methods, the deep learning methods are reported to show superior performances. Jin et al. (47) suggested a CNN algorithm as an alternative to the regularized iterative algorithms based on the observation that the inverse problems defined by a convolution operator are iteratively solved by repeated convolutions and point-wise nonlinearities. Furthermore, Jifara et al. (4) and Zhang et al. (6) demonstrated that the residual learning framework, which involves training the network to separate the noise from a noisy observation, can boost the denoising performance. In addition, Lee et al. (48) also proposed a residual learning method for solving compressed sensing reconstruction by showing that the noisy artifact originating from the randomly under-sampled k-space has a topologically simpler manifold than that of the original images. Benou et al. (42) proposed an ensemble of voxel-wise DNNs for spatiotemporal denoising in DCE-MRI. Kyathanahally et al. (49) proposed a deep learning approach for the detection and removal of ghosting artifacts in MR spectroscopy by training a huge simulated spectra database with and without ghosting artifacts. Spectrograms were fed to the CNN-structured network in order to allow for the detection of the ghosting artifacts, and an encoder-decoder network was designed for the removal of the artifacts.

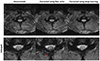
MRI has unique characteristics of artifacts due to its spatial encoding schemes and reconstruction algorithms. One of the most common artifacts in MRI is caused by various motions of a subject, which results in the pernicious construction of a k-space, leading to contamination of the entire image. Many techniques have been proposed to tackle this problem, and these can be categorized as either prospective or retrospective methods (50 51 52 53 54 55). The conventional techniques used additional motion detectors or external devices such as navigators (55) or motion tracking systems (52). Several methods have been proposed to use only the acquired k-space only by minimizing a cost function for the motion estimation (50 51 54). However, computational complexity has been a limiting factor of these techniques because of the high degree of freedom (i.e., six for a rigid motion) and the variety of motions that can occur. In order to overcome this, the deep learning methods that can address the computational challenge using datadriven power have been applied for motion correction and detection. Several studies have demonstrated the feasibility of deep learning applications to the retrospective motion correction, indicating the reduction of motion artifacts in the brain (56 57 58), cervical spine (59), and liver (60). Figure 6 shows the results from the deep learning-based retrospective motion correction for the cervical spine gradient echo images (59). The common training schemes of previous studies were image-to-image approaches, using the CNN structures with a set of the motion-corrupted and motion-free images. Another study attempted to automatically detect motion artifacts through the binary classification of ‘motion’ or ‘no motion’ using CNN (61).

Image super-resolution is a well-known ill-posed problem that can result in multiple outputs for a single input, with the objective of restoring high-resolution images from low-resolution images. Deep learning involves successfully replacing the conventional methods as a state-of-the-art algorithm to solve this problem in natural image applications. Deep learning also shows superior performance to the conventional interpolation methods in MRI applications in the brain (62 63 64 65) and musculoskeletal system (66). Pham et al. (62) used a landmark method named SRCNN and demonstrated the super-resolution applications using deep learning (62 67). Kim et al. (65) and Shi et al. (63) proposed a CNN with a residual framework for training mapping between the low resolution image and the high frequency portions of the k-space (63 65). In addition, Kim et al. (65) suggested incorporating images with different contrasts as well as using an adversarial network. A generative adversarial network (GAN) was also used in Chen et al. (64), who proposed a dense-net structure for generation network. Chaudhari et al. (66) used deep learning for generating thin-slice musculoskeletal images from those of higher slice thickness while maintaining high in-plane resolution, in order to reduce scan time.

Deep learning also addresses the artifacts observed in specific pulse sequences. For example, a single-shot echo planar imaging (EPI) suffers from the so-called Nyquist (N/2) ghosting artifact, notably at high field. The Nyquist ghosting artifact is caused by the misalignments between odd and even k-space lines, mainly caused by eddy current-induced gradient delays and off-resonance. Lee et al. (70) proposed a reference-free EPI ghost correction method using a deep learning approach which has been reported to improve the image quality and decrease the computation time as compared to the conventional method. Deep learning can perform direct improvement of the image quality by using the data-driven power. Kim et al. (71) demonstrated that the CNN approach led to improvements in ASL perfusion images quality using a smaller number of subtraction images. The results were shown to outperform the conventional methods in the quantitative measurements. Ryu et al. (69) showed that improved fluid attenuated inversion recovery (FLAIR) images can be synthesized with a combination of the generated images obtained from the synthetic MRI protocol, known as magnetic resonance imaging compilation (MAGIC) (68). The FLAIR images generated from the synthetic MRI protocol exhibit several common artifacts due to the imperfect model fitting (71). The deep learning method successfully corrected these artifacts, preserving the contrast of conventional FLAIR images, as shown in Figure 7.

Parameter Mapping

Quantitative MR parameter mapping is also an area where deep learning is actively applied due to its capability for function approximation. The measurable information that can be quantified from MRI is extensive. Examples include estimating the parameters from the analytical signal model and measuring the volume of lesions in the image. In this section, we limit our scope to the applications of the deep learning techniques in the model-based parameter mapping, since the measurement of the structural parameters has a strong association with the segmentation problems, as covered in the next section. Golkov et al. (72) proposed a q-space deep learning method which enables the estimation of diffusion kurtosis measured from twelve-fold less data. Bertleff et al. (73) proposed a neural network approach used for voxel-wise diffusion parameter mapping, which was found to have superior robustness and sensitivity to the state-of-the-art model fitting method. Both studies applied neural networks to voxel-wise estimation. An artificial neural network was designed as a multilayer perceptron and was trained to predict microstructural parameters from the acquired data. A similar approach was used to estimate the oxygen extraction fraction (OEF) from the gradient-echo sample spin-echo (GESSE) sequence (74). With a given quantitative signal model, an artificial synthetic dataset was generated and used as a training set. In addition, due to its rapid forward processing time, this approach is a promising method that has great potential to be applied to the clinical use of quantitative MR. The multilayer perceptron model is also applicable to the MR relaxation parameters such as T1, T2, and proton density. Lee et al. (75) proposed a multilayer perceptron method for T2 mapping (Fig. 8) using a multi-echo spin-echo sequence. In order to accurately estimate T2, the effects of B1 inhomogeneity were also considered, and the complexity of the model has been overcome using the proposed artificial neural network method, which requires a long processing time in the conventional manners (75).

Recently, the deep learning technique was applied to overcome the limitations of the conventional reconstruction method of magnetic resonance fingerprinting (MRF), which uses variations in the pulse sequence parameters to generate unique signal evolutions for multi-parametric measurements in a single scan (76). The conventional MRF reconstruction method involves dictionary matching with the measured signal using the dictionary generated by simulating the magnetization evolution. In order to ensure reconstruction accuracy, a large size of the dictionary is necessary, but this requires memory and computational power, which are the limiting factors for a clinical application of MRF. Cohen et al. (77) proposed a deep learning approach based on the multilayer perceptron structure, which was trained with the dictionary to approximate the function which maps the measured signals to the multiple parameters. Compared to the conventional methods, dramatic reductions in reconstruction time as well as robustness to the noise were reported.

Deep learning can also be used effectively in problems where it is not practical to obtain a gold standard reference. Quantitative susceptibility mapping (QSM), which involves estimation from phase images of gradient echo images, is a representative example (79). For QSM calculation, at least three independent scans with different head orientations are required in order to obtain a gold standard reference (80). To avoid this impractical scan issue, non-linear optimization methods have been proposed for the reconstruction of QSM from a single-scan using various prior information (79 81 82 83). A deep learning approach was proposed, which takes advantage of the deep neural network to map the gold standard QSM (as reconstructed from multiple scans) from a single orientation data (78). The U-net structure was modified to process the data with 3D computations, which supports the physical processing of the magnetic dipoles. The network architecture and representative test images from the network for QSM reconstruction are presented in Figure 9.

The use of deep learning fosters great potential in MR parameter mapping, demonstrating the ability to learn the direct mapping of the gold standard values with a fast reconstruction time. In addition, while the conventional parameter mapping methods have been preceded by the formation of the analytical models, the deep learning method indicates the potential for estimation with sufficient data generated by simulations of experiments, even without any analytical model. However, current deep learning studies reveal some limitations that hinder the practical use of deep learning methods in parameter mapping. The end-to-end property of the deep neural networks do not provide any clarity as to how they derive the results, or the corresponding accountability of their derivations. Furthermore, since the outcome of the network depends entirely on the training dataset, it is also difficult to predict how the network would operate on inputs that they have never encountered. This issue is practically important, because the boundaries and distributions of parameters for clinical data are difficult to define. The robustness over variable scan parameters (TR, TE, etc.) is also difficult, since the input of the network should be within the domain of the trained data. In order to overcome these drawbacks, attempts have been made to understand how the network works (84 85 86) and to generalize learning, including transfer learning (87 88 89) or interpretable deep learning (90 91).

Image Contrast Conversion

Deep learning has also shown potential in the contrast conversion of various medical images. Contrast conversion involves transforming one type of medical image to another without actually acquiring the images. Once the contrast conversion has been completely learned, synthesizing one type of medical images with other types, having different contrasts or modalities, is made possible. For example, a CT image can be reconstructed with a MR image without an actual scan of a CT protocol. It is difficult to completely replace the original CT images with the synthesized CT images for general purpose, but it may be useful for limited applications, such as attenuation correction for integrated MR-PET systems. Liu et al. (92) demonstrated that the generated synthetic CT images can be used to calculate attenuation maps for accurate PET quantification. Using the synthetic deep learned CT image to calculate the attenuation map outperforms other previous techniques using MR images alone, including atlas-based methods and segmentation-based methods for brain imaging. Research on the generation of accurate CT images with MR images is of great interest, and many related studies have been conducted (93 94 95). For example, Jun et al. (96) showed that contrast-enhanced 3D gradient recalled echo (CE 3D-GRE) images can be transformed into black-blood (BB) images. They also demonstrated that the sensitivity of the synthetic BB images is almost equivalent to that of the actual BB images, and interestingly, the synthetic BB images outperformed the actual images in terms of false positive lesion detection error. On the other hand, Gong et al. (97) showed that full dose gadolinium-enhanced MR images can be synthesized with low dose MR images. This study demonstrated the potential for reducing the necessary gadolinium dose for a patient using the deep learning method. Ryu et al. (98) showed the potential utility of the deep learning based synthesized magnetization-prepared rapid gradient-echo (MPRAGE) images from multiecho gradient-echo images by comparing the accuracies of the brain segmentation results between the synthesized and actual MPRAGE images. Figure 10 shows the representative test images of the input, output, and ground truth data for the deep neural network.

In order to train the network to successfully perform contrast conversion, data pre-processing steps, including intensity normalization and co-registration, are crucial. Another important factor is the architecture of the deep neural network. For the image transformation, fully convolutional networks such as U-Net (99) are preferred over fully-connected networks, because they do not have fully-connected layers and thus allow for spatial invariance (100). Finally, the selection of the loss function highly affects the synthesized output images. Euclidean losses, called pixel-wise losses, such as mean squared error loss and mean absolute error loss, were conventionally used. However, these losses are reported to cause blurring in cases of uncertainty in the inference. Recently, loss functions mimicking human perceptions have also been proposed, such as perceptual loss (101) and generative adversarial network loss (GAN) (102), but using those loss functions for medical images would require a more careful validation process.

Image Segmentation

The segmentation of MR images is an essential step for the quantitative assessment of various applications such as identifying the margins of a lesion for surgical planning or measuring the volumes of the organs for a population study. The typical image segmentation algorithm depends on the spatial properties of image intensity values. Specifically, discontinuity and similarity are the key properties for the segmentation of a specific object. However, it is difficult to establish a generalized method for the intensity-based segmentation, because the image intensities of most MR images are not quantitative and are largely influenced by environmental factors such as imaging hardware, protocol, and noises. Although several successful automatic segmentation algorithms have been developed and used in specific applications, such as brain segmentation from T1-weighted images (103 104), these methods involve complex and extensive processing steps (which are sensitive to input variations) and often require manual interventions for abnormal cases. In addition, there is still a lack of robust algorithms available in many areas requiring segmentation tasks. Further, advances in deep learning architectures such as U-net (99) or DeepLab (9) and large amounts of image data are expected to solve the limitations of traditional methods and improve the performance in MR image segmentation applications. Recently, deep learning methods have shown the best performances in most contests dealing with MR image segmentations, such as the brain tumor segmentation challenge. Recent methods for MR image segmentations have mostly used 3D operations to reflect the object's spatial context in 3D space. In order to increase robustness, ensemble methods using combinations of differently-constructed architectures have often been adopted for MR image segmentations. Kamnitsas et al. (105) proposed ensembles of multiple models and architectures for a robust brain tumor segmentation from MR images of four different contrast (FLAIR, T1, contrast-enhanced T1 and T2). They used the multiple 3D CNNs, which have different architectures and characteristics, in order to obtain more reliable estimates using the advantages of each model. Rajchl et al. (106), developed the deep learning-based brain segmentation tool from T1-weighted MR images using the ResNet architecture (7) as an encoder and multiple fully connecter networks as a decoder. As compared to the traditional methods, the method developed by Rajchl et al. (106) shows a remarkably fast processing time (90 seconds per a subject) with good reproducibility and robustness. In addition, deep learning-based methods are actively applied in various MR image segmentation applications such as brain tumors (107 108 109), prostate cancer (110 111 112), stroke lesions (105 113), and knee cartilage (114 115 116).

Tools for Deep Learning

In this section, we introduce research tools for implementing deep learning algorithm for MR image processing applications. Various research tools have been used in the MRI research community, but MATLAB (https://www.mathworks.com/) and Python (https://www.python.org/) are currently the most popular, due to their easy interfaces and rich libraries. In recent years, it has become relatively easy to begin conducting a deep learning study, because several graphical process unit available deep learning libraries are actively distributed and updated for both the MATLAB and python interfaces. For the MATLAB interface, MatConvNet (http://www.vlfeat.org/matconvnet/) has been distributed for various CNN applications, and MATLAB has recently started to offer native support for deep learning libraries. For the Python interface, Tensorflow (https://www.tensorflow.org/) and Pytorch (https://pytorch.org) are the most popular open-source deep learning libraries, and they are widely used in various research fields today. Interestingly, the deep learning algorithms implemented using these open-source deep learning libraries are also being shared by research communities worldwide. The deep learning technologies are developing, spreading, and being evaluated very rapidly with these open-source projects.

In conclusion, this article, the basic concepts of deep learning have been briefly explained, and recent deep learning studies on various MR image processing applications have been reviewed. As is the case in other data processing fields, the role of deep learning is expected to become increasingly important in the field of MR image processing. In addition, deep learning is also currently being actively applied in the fields of MR image analysis and interpretation, such as computer-aided diagnosis. Advances in image processing area through deep learning will help areas such as computer-aided detection or diagnosis as well. Although deep learning methods have shown remarkable performances in many MR image processing applications, care should be taken in applying them due to their unclear working mechanisms. In addition, it is important to build a database that contains fine quality and large amounts of data, since the performance of a deep learning method depends on the training dataset used. For clinical applications, analysis of how the deep learning method produces the outputs for various inputs from different imaging conditions including different scanners, pulse sequences, or reconstruction methods should be conducted. One of the most important goals of MRI is to acquire accurate information from the reconstructed images for the purpose of patient care or scientific research. Therefore, the development and evaluation of the deep learning-based methods should also go along with this primary goal.

Figures and Tables

Fig. 1

(a) Overall process of the learning process for the simplified version of the neural network, which is the most widely used deep learning architecture in image processing applications. The nodes of the previous layer can be connected to each node of the next layer in various ways. (b) Fully-connected layer. (c) Locally-connected layer. (d) Locally-connected layer with multiple channels.

Fig. 2

Examples showing the ability of deep learning to generate realistic fake images. (a) Representative test images from the trained network for generating either pizza images from T1-weighted MR images or T1-weighted MR images from pizza images. (b) Representative test images from the tr ained network for generating MR diffusion-weighted images from actual CT images. The network generated the realistic synthesized diffusion-weighted image from the actual CT image. However, this generated diffusion-weighted image does not include the pathologic information which appears on the corresponding actual diffusion-weighted image. These two examples were generated using the generative adversarial networks, which are popular deep neural networks used for image-to-image translation tasks (18 19 20).

Fig. 3

Splitting data into training, valid, and test sets is generally recommended so as to avoid overfitting and evaluate the performance objectively. The optimally fitted network shows similarly good performances for all three data sets.

Fig. 4

Simple example of the effect of data augmentation on deep learning. Data augmentation is generally recommended in order to increase the robustness for input data variances. The slightly modified architecture of automated transform by manifold approximation (21) was used in this example.

Fig. 5

Tools for MRI image reconstruction. The intersection of the individual solution distributions from the tools may represent the most likely solution.

Fig. 6

Retrospective motion correction using deep learning. Motion corrupted image (left), compensated images with 1D navigator (center), and deep learning approach (right). The second row shows the enlarged images of the cervical spinal cord region.

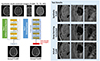Fig. 7

Artifact correction for synthetic fluid attenuated inversion recovery (FLAIR) images using deep learning. Several artifacts are common on conventional model-based synthetic FLAIR images (68). The deep learning method suggested by Ryu et al. (69) successfully corrected these artifacts, thereby preserving the contrast of conventional FLAIR images (70).

Fig. 8

Multilayer perceptron method for T2 mapping using a multi-echo spin-echo sequence. The effects of B1 inhomogeneity were also considered, and the complexity of the model has been overcome using the proposed method (75).

Fig. 9

Deep neural network trained to map the gold standard QSM (COSMOS) reconstructed from multiple scans) from a single orientation phase data (78).

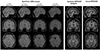Fig. 10

Synthesized magnetization-prepared rapid gradient-echo (MPRAGE) images from multiecho gradient-echo images. The deep neural network (3D U-Net) was used in this example (98).

Acknowledgments

This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (NRF-2017R1D1A1B03030772).

References

1. Krizhevsky A, Sutskever I, Hinton GE. ImageNet classification with deep convolutional neural networks. In : NIPS 2012: Neural Information Processing Systems; Lake Tahoe, Nevada. 2012. p. 1097–1105.

2. Hinton G, Deng I, Yu D, et al. Deep neural networks for acoustic modeling in speech recognition: the shared views of four research groups. IEEE Signal Processing Magazine. 2012; 29:82–97.

3. Sutskever I, Vinyals O, Le QV. Sequence to sequence learning with neural networks. In : Proceedings of the 27th International Conference on Neural Information Processing Systems - Vol 2; 2014. p. 3104–3112.

4. Jifara W, Jiang F, Rho S, Cheng M, Liu S. Medical image denoising using convolutional neural network: a residual learning approach. J Supercomput. 2017; 1–15.

5. Vincent P, Larochelle H, Lajoie I, Bengio Y, Manzagol PA. Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion. J Mach Learn Res. 2010; 11:3371–3408.

6. Zhang K, Zuo W, Chen Y, Meng D, Zhang L. Beyond a Gaussian denoiser: residual learning of deep CNN for image denoising. IEEE Trans Image Process. 2017; 26:3142–3155.

7. He K, Zhang X, Ren S, Sun J. Deep residual learning for image recognition. In : Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR); 2016. p. 770–778.

8. Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv:1409.1556. 2014.

9. Chen LC, Papandreou G, Kokkinos I, Murphy K, Yuille AL. DeepLab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected CRFs. IEEE Trans Pattern Anal Mach Intell. 2018; 40:834–848.

10. Noh H, Hong S, Han B. Learning deconvolution network for semantic segmentation. In : Proceedings of the IEEE International Conference on Computer Vision (ICCV); 2015. p. 1520–1528.

11. LeCun Y, Bengio Y, Hinton G. Deep learning. Nature. 2015; 521:436–444.

12. Glorot X, Bordes A, Bengio Y. Deep sparse rectifier neural networks. In : Proceedings of the 14th International Conference on Artificial Intelligence and Statistics (AISTATS), 2011. Volume 15 of JMLR: W&CP 15; 2011. p. 315–323.

13. LeCun Y, Boser B, Denker JS, et al. Handwritten digit recognition with a back-propagation network. Advances in neural information processing system 2. 1990. p. 396–404.

14. LeCun Y, Bottou L, Bengio Y, Haffner P. Gradient-based learning applied to document recognition. Proceedings of the IEEE. 1998; 86:2278–2324.

15. Goodfellow I, Bengio Y, Courville A, Bengio Y. Deep learning. Cambridge: MIT Press;2016.

16. Schmidhuber J. Deep learning in neural networks: an overview. Neural Netw. 2015; 61:85–117.

17. Szegedy C, Liu W, Jia Y, et al. Going deeper with convolutions. In : Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR); 2015. p. 1–9.

18. Goodfellow I, Pouget-Abadie J, Mirza M, et al. Generative adversarial nets. In : Proceedings of the 27th International Conference on Neural Information Processing Systems; 2014. 2:p. 2672–2680.

19. Isola P, Zhu J-Y, Zhou T, Efros AA. Image-to-image translation with conditional adversarial networks. In : Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR); 2017. p. 1125–1134.

20. Zhu J-Y, Park T, Isola P, Efros AA. Unpaired image-toimage translation using cycle-consistent adversarial networks. In : Proceedings of the IEEE International Conference on Computer Vision (ICCV); 2017. p. 2223–2232.

21. Zhu B, Liu JZ, Cauley SF, Rosen BR, Rosen MS. Image reconstruction by domain-transform manifold learning. Nature. 2018; 555:487–492.

22. Lauterbur PC. Image formation by induced local interactions. Examples employing nuclear magnetic resonance. 1973. Clin Orthop Relat Res. 1989; 3–6.

23. Mansfield P, Maudsley AA. Medical imaging by NMR. Br J Radiol. 1977; 50:188–194.

24. Griswold MA, Jakob PM, Heidemann RM, et al. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn Reson Med. 2002; 47:1202–1210.

25. Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magn Reson Med. 1999; 42:952–962.

26. Sodickson DK, Manning WJ. Simultaneous acquisition of spatial harmonics (SMASH): fast imaging with radiofrequency coil arrays. Magn Reson Med. 1997; 38:591–603.

27. Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med. 2007; 58:1182–1195.

28. Wang G, Ye JC, Mueller K, Fessler JA. Image reconstruction is a new frontier of machine learning. IEEE Trans Med Imaging. 2018; 37:1289–1296.

29. Boyd S, Vandenberghe L. Convex optimization. New York: Cambridge University Press;2004. p. 127–214.

30. Han Y, Yoo J, Kim HH, Shin HJ, Sung K, Ye JC. Deep learning with domain adaptation for accelerated projection-reconstruction MR. Magn Reson Med. 2018; 80:1189–1205.

31. Ye JC, Han Y, Cha E. Deep convolutional framelets: a general deep learning framework for inverse problems. SIAM J Imaging Sci. 2018; 11:991–1048.

32. Lee D, Yoo J, Ye JC. Deep residual learning for compressed sensing MRI. In : IEEE 14th International Symposium on Biomedical Imaging (ISBI); 2017. p. 15–18.

33. Hammernik K, Klatzer T, Kobler E, et al. Learning a variational network for reconstruction of accelerated MRI data. Magn Reson Med. 2018; 79:3055–3071.

34. Knoll F, Hammernik K, Kobler E, Pock T, Recht MP, Sodickson DK. Assessment of the generalization of learned image reconstruction and the potential for transfer learning. Magn Reson Med. 2019; 81:116–128.

35. Akcakaya M, Moeller S, Weingartner S, Ugurbil K. Scan-specific robust artificial-neural-networks for k-space interpolation (RAKI) reconstruction: Database-free deep learning for fast imaging. Magn Reson Med. 2019; 81:439–453.

36. Yang G, Yu S, Dong H, et al. DAGAN: Deep de-aliasing generative adversarial networks for fast compressed sensing MRI reconstruction. IEEE Trans Med Imaging. 2018; 37:1310–1321.

37. Quan TM, Nguyen-Duc T, Jeong WK. Compressed sensing MRI reconstruction using a generative adversarial network with a cyclic loss. IEEE Trans Med Imaging. 2018; 37:1488–1497.

38. Mardani M, Gong E, Cheng JY, et al. Deep generative adversarial neural networks for compressive sensing MRI. IEEE Trans Med Imaging. 2019; 38:167–179.

39. Hyun CM, Kim HP, Lee SM, Lee S, Seo JK. Deep learning for undersampled MRI reconstruction. Phys Med Biol. 2018; 63:135007.

40. Eo T, Jun Y, Kim T, Jang J, Lee HJ, Hwang D. KIKInet: cross-domain convolutional neural networks for reconstructing undersampled magnetic resonance images. Magn Reson Med. 2018; 80:2188–2201.

41. Aggarwal HK, Mani MP, Jacob M. MoDL: Model-based deep learning architecture for inverse problems. IEEE Trans Med Imaging. 2019; 38:394–405.

42. Benou A, Veksler R, Friedman A, Riklin Raviv T. Ensemble of expert deep neural networks for spatio-temporal denoising of contrast-enhanced MRI sequences. Med Image Anal. 2017; 42:145–159.

43. Dabov K, Foi A, Katkovnik V, Egiazarian K. Image restoration by sparse 3D transform-domain collaborative filtering. In : Image Processing: Algorithms and Systems VI; International Society for Optics and Photonics;2008. p. 681207.

44. Elad M, Aharon M. Image denoising via sparse and redundant representations over learned dictionaries. IEEE Trans Image Process. 2006; 15:3736–3745.

45. Zoran D, Weiss Y. From learning models of natural image patches to whole image restoration. In : IEEE International Conference on Computer Vision (ICCV); 2011. p. 479–486.

46. Gu S, Zhang L, Zuo W, Feng X. Weighted nuclear norm minimization with application to image denoising. In : IEEE Conference on Computer Vision and Pattern Recognition (CVPR); 2014. p. 2862–2869.

47. Jin KH, McCann MT, Froustey E, Unser M. Deep convolutional neural network for inverse problems in imaging. IEEE Trans Image Process. 2017; 26:4509–4522.

48. Lee D, Yoo J, Tak S, Ye J. Deep residual learning for accelerated mri using magnitude and phase networks. IEEE Trans Biomed Eng. 2018; 65:1985–1995.

49. Kyathanahally SP, Doring A, Kreis R. Deep learning approaches for detection and removal of ghosting artifacts in MR spectroscopy. Magn Reson Med. 2018; 80:851–863.

50. Atkinson D, Hill DL, Stoyle PN, Summers PE, Keevil SF. Automatic correction of motion artifacts in magnetic resonance images using an entropy focus criterion. IEEE Trans Med Imaging. 1997; 16:903–910.

51. Loktyushin A, Nickisch H, Pohmann R, Scholkopf B. Blind retrospective motion correction of MR images. Magn Reson Med. 2013; 70:1608–1618.

52. Ooi MB, Krueger S, Thomas WJ, Swaminathan SV, Brown TR. Prospective real-time correction for arbitrary head motion using active markers. Magn Reson Med. 2009; 62:943–954.

53. Maclaren J, Armstrong BS, Barrows RT, et al. Measurement and correction of microscopic head motion during magnetic resonance imaging of the brain. PLoS One. 2012; 7:e48088.

54. Haskell MW, Cauley SF, Wald LL. TArgeted Motion Estimation and Reduction (TAMER): Data Consistency Based Motion Mitigation for MRI Using a Reduced Model Joint Optimization. IEEE Trans Med Imaging. 2018; 37:1253–1265.

55. Kober T, Marques JP, Gruetter R, Krueger G. Head motion detection using FID navigators. Magn Reson Med. 2011; 66:135–143.

56. Sommer K, Brosch T, Rafael W, et al. Correction of motion artifacts using a multi-resolution fully convolutional neural network. In : Proceeding ISMRM Scientific Meeting & Exhibition; 2018. p. 1175.

57. Johnson PM, Drangova M. Motion correction in MRI using deep learning. In : Proceeding ISMRM Scientific Meeting & Exhibition; 2018. p. 4098.

58. Pawar K, Chen Z, Shah J, Egan GF. Motion correction in MRI using deep convolutional neural network. In : Proceeding ISMRM Scientific Meeting & Exhibition; 2018. p. 1174.

59. Lee H, Ryu K, Nam Y, Lee J, Kim DH. Reduction of respiratory motion artifact in c-spine imaging using deep learning: Is substitution of navigator possible? In : Proceeding ISMRM Scientific Meeting & Exhibition; 2018. p. 2660.

60. Tamada D, Kromrey M-L, Onishi H, Motosugi U. Method for motion artifact reduction using a convolutional neural network for dynamic contrast enhanced MRI of the liver. arXiv preprint arXiv 2018:1807.06956.

61. Meding K, Loktyushin A, Hirsch M. Automatic detection of motion artifacts in MR images using CNNS. In : 42nd IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP); 2017. p. 811–815.

62. Pham CH, Ducournau A, Fablet R, Rousseau F. Brain MRI super-resolution using deep 3D convolutional networks. In : IEEE 14th International Symposium on Biomedical Imaging (ISBI); 2017. p. 197–200.

63. Shi J, Liu Q, Wang C, Zhang Q, Ying S, Xu H. Superresolution reconstruction of MR image with a novel residual learning network algorithm. Phys Med Biol. 2018; 63:085011.

64. Chen Y, Xie Y, Zhou Z, Shi F, Christodoulou AG, Li D. Brain MRI super resolution using 3D deep densely connected neural networks. In : 2018 IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018); 2018. p. 739–742.

65. Kim KH, Do WJ, Park SH. Improving resolution of MR images with an adversarial network incorporating images with different contrast. Med Phys. 2018; 45:3120–3131.

66. Chaudhari AS, Fang Z, Kogan F, et al. Super-resolution musculoskeletal MRI using deep learning. Magn Reson Med. 2018; 80:2139–2154.

67. Dong C, Loy CC, He K, Tang X. Image Super-Resolution Using Deep Convolutional Networks. IEEE Trans Pattern Anal Mach Intell. 2016; 38:295–307.

68. Tanenbaum LN, Tsiouris AJ, Johnson AN, et al. Synthetic MRI for Clinical Neuroimaging: Results of the Magnetic Resonance Image Compilation (MAGiC) Prospective, Multicenter, Multireader Trial. AJNR Am J Neuroradiol. 2017; 38:1103–1110.

69. Ryu K, Nam Y, Gho SM, et al. Data-driven synthetic MRI FLAIR artifact correction via deep neural network. J Magn Reson Imaging. 2019; [Epub ahead of print].

70. Lee J, Han Y, Ye JC. k-Space Deep Learning for Reference-free EPI Ghost Correction. arXiv preprint arXiv 2018:1806.00153v2.

71. Kim KH, Choi SH, Park SH. Improving Arterial Spin Labeling by Using Deep Learning. Radiology. 2018; 287:658–666.

72. Golkov V, Dosovitskiy A, Sperl JI, et al. q-Space Deep Learning: Twelve-Fold Shorter and Model-Free Diffusion MRI Scans. IEEE Trans Med Imaging. 2016; 35:1344–1351.

73. Bertleff M, Domsch S, Weingartner S, et al. Diffusion parameter mapping with the combined intravoxel incoherent motion and kurtosis model using artificial neural networks at 3 T. NMR Biomed. 2017; 30:[Epub ahead of print].

74. Domsch S, Murle B, Weingartner S, Zapp J, Wenz F, Schad LR. Oxygen extraction fraction mapping at 3 Tesla using an artificial neural network: a feasibility study. Magn Reson Med. 2018; 79:890–899.

75. Lee D, Jung W, Lee J, et al. SafeNet: Artificial neural network for real-time T2 mapping with quality assurance. In : Joint Annual Meeting ISMRM-ESMRMB; ISMRM;2018. p. 2277.

76. Ma D, Gulani V, Seiberlich N, et al. Magnetic resonance fingerprinting. Nature. 2013; 495:187–192.

77. Cohen O, Zhu B, Rosen MS. MR fingerprinting Deep RecOnstruction NEtwork (DRONE). Magn Reson Med. 2018; 80:885–894.

78. Yoon J, Gong E, Chatnuntawech I, et al. Quantitative susceptibility mapping using deep neural network: QSMnet. Neuroimage. 2018; 179:199–206.

79. Shmueli K, de Zwart JA, van Gelderen P, Li TQ, Dodd SJ, Duyn JH. Magnetic susceptibility mapping of brain tissue in vivo using MRI phase data. Magn Reson Med. 2009; 62:1510–1522.

80. Liu T, Spincemaille P, de Rochefort L, Kressler B, Wang Y. Calculation of susceptibility through multiple orientation sampling (COSMOS): a method for conditioning the inverse problem from measured magnetic field map to susceptibility source image in MRI. Magn Reson Med. 2009; 61:196–204.

81. Liu T, Liu J, de Rochefort L, et al. Morphology enabled dipole inversion (MEDI) from a single-angle acquisition: comparison with COSMOS in human brain imaging. Magn Reson Med. 2011; 66:777–783.

82. Wharton S, Schafer A, Bowtell R. Susceptibility mapping in the human brain using threshold-based k-space division. Magn Reson Med. 2010; 63:1292–1304.

83. de Rochefort L, Liu T, Kressler B, et al. Quantitative susceptibility map reconstruction from MR phase data using bayesian regularization: validation and application to brain imaging. Magn Reson Med. 2010; 63:194–206.

84. Papyan V, Romano Y, Elad M. Convolutional Neural Networks Analyzed via Convolutional Sparse Coding. J Mach Learn Res. 2017; 83:1–52.

85. Wiatowski T, Bolcskei H. A Mathematical Theory of Deep Convolutional Neural Networks for Feature Extraction. IEEE Trans Inf Theory. 2018; 64:1845–1866.

86. Ye JC, Han Y, Cha E. Deep Convolutional Framelets: A General Deep Learning Framework for Inverse Problems. SIAM J Imaging Sci. 2018; 11:991–1048.

87. Razavian AS, Azizpour H, Sullivan J, Carlsson S. CNN features off-the-shelf: an astounding baseline for recognition. arXiv preprint arXiv 2014:1403.6382.

88. Yosinski J, Clune J, Bengio Y, Lipson H. How transferable are features in deep neural networks?. In : Ghahramani Z, Welling M, Cortes C, Lawrence ND, Weinberger KQ, editors. Advances in neural information processing systems 27. Curran Associates, Inc.;2014. p. 3320–3328.

89. Knoll F, Hammernik K, Kobler E, Pock T, Recht MP, Sodickson DK. Assessment of the generalization of learned image reconstruction and the potential for transfer learning. Magn Reson Med. 2019; 81:116–128.

90. Fong RC, Vedaldi A. Interpretable explanations of black boxes by meaningful perturbation. In : IEEE International Conference on Computer Vision (ICCV); 2017. p. 3449–3457.

91. Zeiler MD, Fergus R. Visualizing and understanding convolutional networks. Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics). Volume 8689 LNCS, No. PART 1. Springer Verlag;2014. p. 818–833.

92. Liu F, Jang H, Kijowski R, Bradshaw T, McMillan AB. Deep learning MR imaging-based attenuation correction for PET/MR imaging. Radiology. 2018; 286:676–684.

93. Han X. MR-based synthetic CT generation using a deep convolutional neural network method. Med Phys. 2017; 44:1408–1419.

94. Xiang L, Wang Q, Nie D, et al. Deep embedding convolutional neural network for synthesizing CT image from T1-Weighted MR image. Med Image Anal. 2018; 47:31–44.

95. Wolterink JM, Dinkla AM, Savenije MHF, Seevinck PR, van den Berg CAT, Isgum I. Deep MR to CT synthesis using unpaired data. In : International Workshop on Simulation and Synthesis in Medical Imaging; Cham: Springer;2017. p. 14–23.

96. Jun Y, Eo T, Kim T, et al. Deep-learned 3D black-blood imaging using automatic labelling technique and 3D convolutional neural networks for detecting metastatic brain tumors. Sci Rep. 2018; 8:9450.

97. Gong E, Pauly JM, Wintermark M, Zaharchuk G. Deep learning enables reduced gadolinium dose for contrast-enhanced brain MRI. J Magn Reson Imaging. 2018; 48:330–340.

98. Ryu K, Shin NY, Kim DH, Nam Y. Synthesizing T1 weighted MPRAGE image from multi echo GRE images via deep neural network. Magn Reson Imaging. 2019; [Epub ahead of print].

99. Ronneberger O, Fischer P, Brox T. U-net: Convolutional networks for biomedical image segmentation. In : International Conference on Medical Image Computing and Computer-assisted Invervention; 2015. p. 234–241.

100. Long J, Shelhamer E, Darrell T. Fully convolutional networks for semantic segmentation. In : Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR); Cham: Springer;2015. p. 3431–3440.

101. Yang Q, Yan P, Zhang Y, et al. Low-Dose CT Image Denoising Using a Generative Adversarial Network With Wasserstein Distance and Perceptual Loss. IEEE Trans Med Imaging. 2018; 37:1348–1357.

102. Nie D, Trullo R, Lian J, et al. Medical image synthesis with context-aware generative adversarial networks. In : Medical Image Computing and Computer-Assisted Intervention-MICCAI 2017-20th International Conference, Proceedings; Springer Verlag;2017. p. 417–425.

103. Fischl B. FreeSurfer. Neuroimage. 2012; 62:774–781.

104. Jenkinson M, Beckmann CF, Behrens TE, Woolrich MW, Smith SM. Fsl. Neuroimage. 2012; 62:782–790.

105. Kamnitsas K, Chen L, Ledig C, Rueckert D, Glocker B. Multi-scale 3D convolutional neural networks for lesion segmentation in brain MRI. Ischemic Stroke Lesion Segment. 2015; 13:46.

106. Rajchl M, Pawlowski N, Rueckert D, Matthews PM, Glocker B. NeuroNet: Fast and robust reproduction of multiple brain image segmentation pipelines. arXiv preprint arXiv 2018:1806.04224.

107. Havaei M, Davy A, Warde-Farley D, et al. Brain tumor segmentation with deep neural networks. Med Image Anal. 2017; 35:18–31.

108. Pereira S, Pinto A, Alves V, Silva CA. Brain tumor segmentation using convolutional neural networks in MRI images. IEEE Trans Med Imaging. 2016; 35:1240–1251.

109. Akkus Z, Galimzianova A, Hoogi A, Rubin DL, Erickson BJ. Deep learning for brain MRI segmentation: state of the art and future directions. J Digit Imaging. 2017; 30:449–459.

110. Liu S, Zheng H, Feng Y, Li W. Prostate cancer diagnosis using deep learning with 3D multiparametric MRI. SPIE Med Imaging. 2017; 10134:1–4.

111. Song Y, Zhang YD, Yan X, et al. Computer-aided diagnosis of prostate cancer using a deep convolutional neural network from multiparametric MRI. J Magn Reson Imaging. 2018; 48:1570–1577.

112. Milletari F, Navab N, Ahmadi S-A. V-net: fully convolutional neural networks for volumetric medical image segmentation. In : 2016 Fourth International Conference on 3D Vision (3DV); IEEE;2016. p. 565–571.

113. Guerrero R, Qin C, Oktay O, et al. White matter hyperintensity and stroke lesion segmentation and differentiation using convolutional neural networks. Neuroimage Clin. 2018; 17:918–934.

114. Norman B, Pedoia V, Majumdar S. Use of 2D U-net convolutional neural networks for automated cartilage and meniscus segmentation of knee MR imaging data to determine relaxometry and morphometry. Radiology. 2018; 288:177–185.

115. Prasoon A, Petersen K, Igel C, Lauze F, Dam E, Nielsen M. Deep feature learning for knee cartilage segmentation using a triplanar convolutional neural network. Med image Comput Comput Assist Interv. 2013; 16:246–253.

116. Zhou Z, Zhao G, Kijowski R, Liu F. Deep convolutional neural network for segmentation of knee joint anatomy. Magn Reson Med. 2018; 80:2759–2770.

TOOLS

Similar articles