Introduction
Age estimation from skeletal remains is an important step in forensic biological identification. Biological identification is an important screening process to provide information to prove identity, as a narrowing of estimation of age range in age estimation is crucial. It can save time and is a key factor in cases involving accidents or homicide.
For an estimation of age at death from skeletal remains, methods can be categorized into two main groups: sub-adult and adult. The estimation of adult age mostly relies on the skeletal degenerative processes [
1]. Various skeletal parts can be utilized as adult age indicators. These include: cranial sutures of the skull [
2], dental wear [
3], the sternal end of the first rib [
4], and fourth rib [
56], the pubic symphysis [
7] and auricular surfaces [
8] of the pelvis, and histomorphometry of the cortical bone [
91011]. In this study the focus of interest is on the vertebral osteophytes. Osteophyte formation on the vertebral column occurs and increases with age, and the development of vertebral osteophytes has been shown to be a general indicator of age [
121314], but the use of vertebral osteophytes for age estimation has not been investigated in Thai people. To address this issue, a study of age estimation from vertebral osteophytes in a Thai population was conducted with the main objective of developing an age estimation equation by using vertebral osteophytes for age-at-death estimation of Thais.
A great deal of research has been conducted into adult age estimation, and several methods can be applied using various parts of the human skeleton [
234567891011]. Key morphological changes included in these studies were those involving cranial sutures, the pubic symphysis, auricular surface, and the sternal ends of first and fourth ribs [
245678]. However, in real situations some bones that are found are barely intact, although some researchers report that in many cases the vertebral column was found to survive even if the limbs and skull had been destroyed by intense burning or by animals [
15]. The presence and development of vertebral osteophytes can also be used as an age determination method [
15], but reliability of the findings are still in doubt and need additional study.
The degenerative process is a crucial factor in most methods developed for estimating adult age [
1]. Vertebral osteophytes have been focused on for their age-related characteristics and can be useful as an age predicting tool [
15].
Degenerative change in the intervertebral discs between the vertebral bodies occur as a natural part of aging. This is an important component of osteoarthritis. Joint movement increases with age, as does reduction of such things as cell proteoglycan, collagen fibers and fluid in the intervertebral discs [
121617]. The degeneration process begins at the nucleus pulposus with cell loss and matrix alteration [
16,
17,
18]. The most significant biochemical change to occur in disc degeneration is loss of proteoglycan [
1617].
Shapiro and Risbud's study is cited [
16]:
This loss is responsible for a fall in osmotic pressure and a loss of hydration. The loss of proteoglycan thus has a major effect on the disc's load-bearing behavior due to damage caused by the collapse of the intervertebral disc and surface cartilage of the joint. The instability of the joint responds by increasing bone formation [
12]. When calcium mask becomes bone regeneration, osteoarthritis produces vertebral osteophytes. These osteophytes arise from proliferating inner annular fibers which undergo metaplasia into cartilage, which calcify and proceed through an endochondral ossification sequence [
16]. Degeneration in the end plate is associated with cell proliferation, cartilage disorganization, and new bone formation [
16]. Thus, vertebral osteophytes can be used to estimate the age. With increasing age an increasing prevalence and severity of disc degeneration has been observed. However, an understanding of what constitutes normal progression remains unclear, as many factors can participate and modify the degenerative process. Genetics is one of the components that can alter this normality by accelerating or decelerating the degenerative process. This change is reviewed elsewhere and includes changes in cell function such as expression levels of genes, the stability of mRNA transcripts or proteins, or the binding affinity of protein interacting partners, caused by genetic variations in or near participating genes. In establishing a cohort for genetic study of disc degeneration, the effect of age must be taken into consideration in terms of subject recruitment and data analyses [
16].
In 1958, Stewart [
19] published a paper which presented some observations on vertebra osteophytosis from the standpoint of age identification. The condition of the superior and inferior borders of each vertebral centrum was rated subjectively on a five-point scale running from 0 (no lipping) to 4 (maximum lipping) [
19]. Later, researchers such as Snodgrass [
20], Van Der Merwe et al. [
21], Kim et al. [
22], and Listi and Manhein [
23] applied this concept to the study of the osteophyte formation. Later studies in Thailand, on the prevalence of vertebral osteophyte formation were conducted by researchers such as Namking et al. [
12] and Chanapa and collegues [
1314]. All of the above mentioned corresponding findings, specifically those related to the formation of osteophytes and age showed a correlation that was statistically significant, but there was still no relationship available for use in age estimation. However, in 2006 Watanabe and Terazawa [
15] defined new grading scores for osteophyte formation. These included four grades, 0, 1, 2, and 3, based on the height of spur, lipping, and bridging at the superior and inferior margins of the cervical, thoracic, and lumbar vertebral bodies. The grading was obtained from the inspection and palpation of 225 bodies during autopsy. The average maximum values of the cervical, thoracic, and lumbar parts, respectively, were defined as the “osteophyte formation index” in each individual and statistical analysis of the integrated data was used to estimate age [
15]. This method was thus accepted as a useful tool in estimating age at death [
15].
The current study is based on the scoring method concept only from Snodgrass [
20] and Watanabe and Terazawa [
15], but different methods for data collection and data analysis include the following:
The Snodgrass study (2004) is cited [
20]:
Each vertebra in the thoracic and lumbar segments of the vertebral column was scored for osteophytosis. This five-stage classification system assesses the stage of osteophytosis separately for each of the superior and inferior surface margins of the vertebral centra. Osteophytes were scored when located on the anterior or lateral regions of the vertebral centra. For each vertebral region a mean score was calculated and a total osteophyte score was calculated by combining the scores of the thoracic and lumbar regions. These scores were calculated by summing the degree of lipping for the superior and inferior margins of the vertebral centra and dividing by the number of vertebral surfaces present in each region (i.e., 24 for the thoracic region and 10 for the lumbar region) [
20].
The Watanabe and Terazawa's study (2006) is cited [
15]:
Evaluated it by inspection and palpation of front surfaces of the cervical, thoracic, and lumbar parts of vertebrae, and bilateral surfaces of the thoracic part, using the previously measured finger's width as a standard indicator. The largest value in each part was used for analysis. And the average of the maximum values, respectively, at cervical, thoracic, and lumbar parts was defined as ‘osteophyte formation index’ in each individual. The degree of osteophyte formation was based on the height of the process of the vertebral column, which represents spur, lipping, and bridging of osteophyte formation at the superior and inferior margins of the vertebral bodies [
15].
Watanabe and Terazawa's study (2006) [
15] used the length of the osteophyte at 0.8 cm as a cut-off point, using a finger-width measurement; the current study could not determine why Watanabe decided on this, but in this study (2019) the length was recorded by digital vernier caliper and measuring tape.
In the current study, all vertebrae (C2–L5) were evaluated for the presence and stage of formation of osteophytes, and the maximum expression was recorded. This staged classification system was used to assess the stage of osteophyte formation of the superior and inferior margins of the vertebral body based on Snodgrass (five-stage classification), Watanabe (four-stage classification), and a new modified score by the length of the vertebral osteophyte (six-stage classification). All scoring methods in all 3 methods have been collected and analyzed according to this study, which is different from previous studies (Snodgrass [
20] and Watanabe and Terazawa [
15]). Mean osteophyte scores were recorded for the entire column and also for each subcategory of vertebrae using a digital vernier caliper and measuring tape. The scores were calculated by dividing the sum of the scores by the total number of vertebrae examined. For example, the mean lumbar osteophyte score was the sum score of all vertebrae divided by 5 (i.e., 6 for the cervical region, 12 for the thoracic region, and 5 for the lumbar region).
This study used a scoring method based on Snodgrass [
20] and Watanabe and Terazawa [
15]. The two previous scoring methods are used because both of these methods have been published and used for estimating age. As well, they're easy, fast and inexpensive. Earlier studies have provided a wide variety of scoring methods, but there are no studies that can be used to estimate an age equation. Previously, Stewart [
19] invented a pattern for the scoring of osteophytes. There are many references to Stewart [
20212223] including Snodgrass; however, the reason why this study makes reference to Snodgrass is because they included clearer descriptions and more pictures than the other studies. Additionally, Watanabe's method is a study that was able to produce equations of age and newly defined grading scores in osteophyte formation.
Go to :

Materials and Methods
This study used vertebral columns from a Thai sample which included cervical (C2–C7), thoracic (T1–T12), and lumbar (L1–L5) vertebrae from 400 individuals (262 males, 138 females) of known sex and age at death from the Forensic Osteology Research Center (FORC), Faculty of Medicine, Chiang Mai University. Ages ranged between 22 and 97 years. The reference sample consisted of Thai individuals who were born between 1913 and 1995.
Individuals with atypical numbers of vertebrae and evidence of vertebral damage were excluded from the study. Each vertebra in the cervical, thoracic and lumbar segments were scored for degree of osteophyte formation according to criteria established by Snodgrass [
20] (five-stage classification), Watanabe and Terazawa [
15] (four-stage classification), and the new modified score by length of vertebral osteophyte (six-stage classification) (
Table 1).
Table 1
Degree of osteophyte formation based on Snodgrass, Watanabe, and Praneatpolgrang

|
Score |
Description |
|
Snodgrass [20] |
Watanabe and Terazawa [15] |
Praneatpolgrang (this study) |
|
0 |
No degenerative change |
No rugged surface |
No rugged surface |
|
1 |
Slight lipping |
Slightly rugged surface |
Rugged surface prominent by less than 2 mm in length |
|
2 |
Moderate lipping |
Degree between score 1 and 3 |
Rugged surface prominent between 2 and 4.99 mm in length |
|
3 |
Severe lipping |
Rugged surface prominent by more than 0.8 cm in height |
Rugged surface prominent between 5 and 8 mm in length |
|
4 |
Ankylosis of adjacent vertebrae |
- |
Rugged surface prominent by more than 8 mm in length |
|
5 |
- |
- |
Fusion of adjacent vertebrae |

From each individual, all vertebrae were evaluated for presence and stage of osteophyte formation; however, the atlas was not considered in the assessment of osteophytes due to the lack of body in the atlas. This staged classification system was used to assess the stage of osteophyte formation of the superior and inferior margins of the vertebral body (
Fig. 1) by evaluating the scores, ranging from no osteophyte to maximum osteophyte. Osteophyte expression can vary considerably within each vertebra, the maximum expression was the one recorded (
Fig. 2). Mean osteophyte scores were recorded for the entire column and also for each subcategory of vertebrae. These scores were calculated by dividing the sum of the scores by the total number of vertebrae examined. For example, the mean lumbar osteophyte score was the sum score of all vertebrae divided by 5 (i.e., 6 for the cervical region, 12 for the thoracic region, and 5 for the lumbar region).
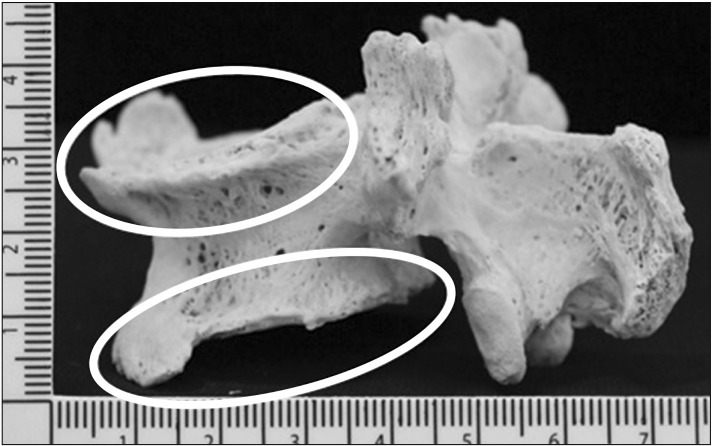 | Fig. 1Position of osteophyte formation at the superior and inferior margins of the vertebral body.
|
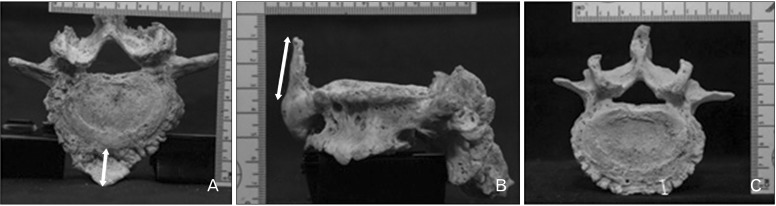 | Fig. 2Praneatpolgrang scoring method. Osteophyte expression can vary considerably within each vertebra, the maximum expression was recorded. Measurement of the length (mm) in the maximum expression by the new modified score by length of vertebral osteophytes: 0, no rugged surface; 1, rugged surface prominent by less than 2 mm in length; 2, rugged surface prominent between 2 and 4.99 mm in length; 3, rugged surface prominent between 5 and 8 mm in length; 4, rugged surface prominent by more than 8 mm in length; and 5, fusion of adjacent vertebrae. Images represent maximum length in the oblique direction (A), vertical direction (B), and horizontal direction (C), respectively.
|
In the statistical tests using descriptive statistics including medians, means, standard deviations, Pearson's correlation test, and Linear regression analysis, we defined P<0.05 significant. All statistical analyses were performed using the SPSS software package (SPSS for Windows, version 20, IBM Corp., Armonk, NY, USA). Statistical analysis was carried out to discover the correlation between the degree of osteophyte formation and age. The following were statistically obtained for each sex: correlation coefficient, regression equation, standard error of estimate between age and degree of osteophyte formation in each vertebra and vertebral column segment.
Go to :

Results
For a combination of both sexes, the mean age and standard deviation were 66.02 and 15.619 years, respectively. There were no significant differences in the mean age of the subjects between males (mean±SD, 65.82±15.534 years) and females (66.41±15.827 years) (
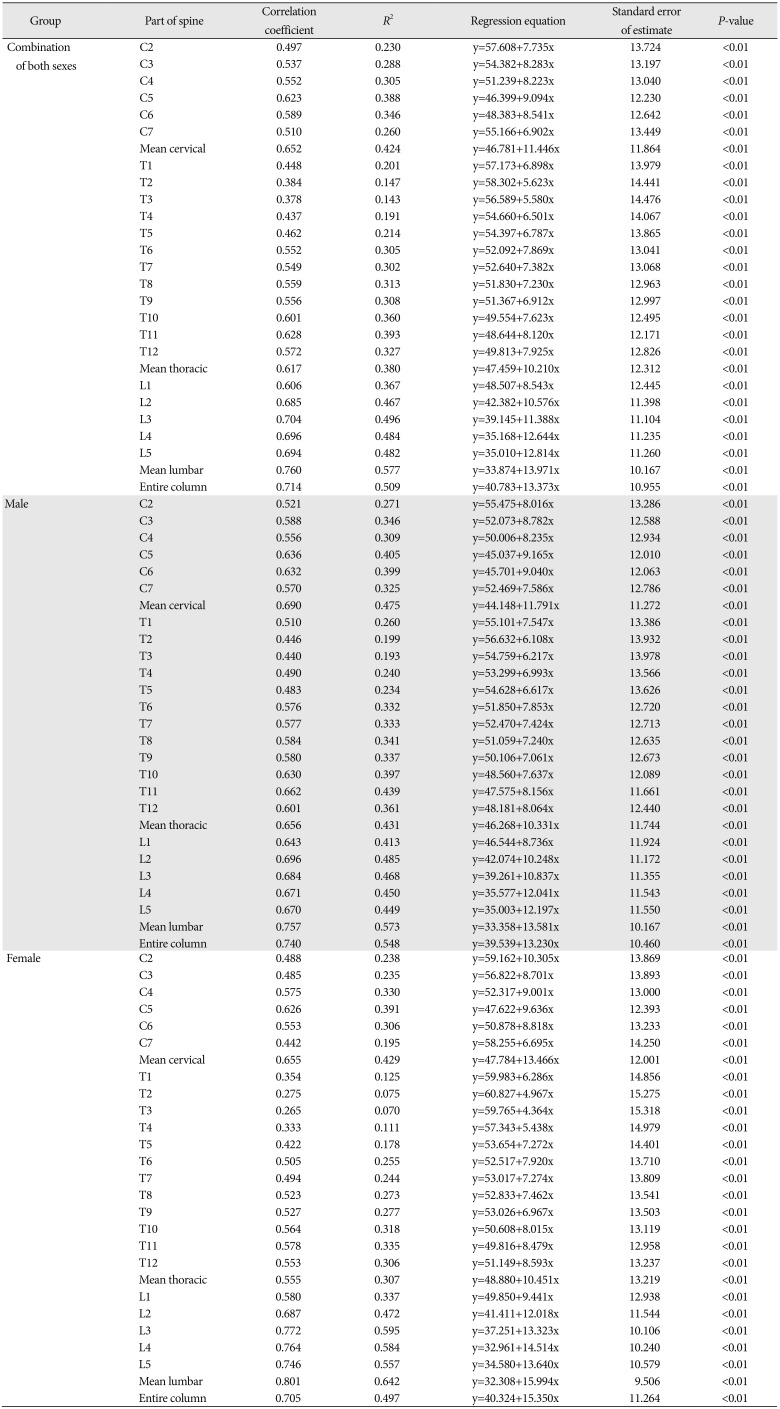
P>0.05, Student's t-test). In all parts of the vertebral column, there was a significant correlation between the score value and the age. The following were statistically obtained for the sexes combined and each sex separately: correlation coefficient, regression equation, standard error of estimate (SE) between the score at each segment of the vertebral column and age, and between the mean in each segment of vertebrae and age. Regression lines of criteria established by Snodgrass (five-stage classification) were y=33.874+13.971x (SE, 10.167), y=33.358+13.581x (SE, 10.167), and y=32.308+15.994x (SE, 9.506) in mean lumbar area for combined sexes, males, and females, respectively (
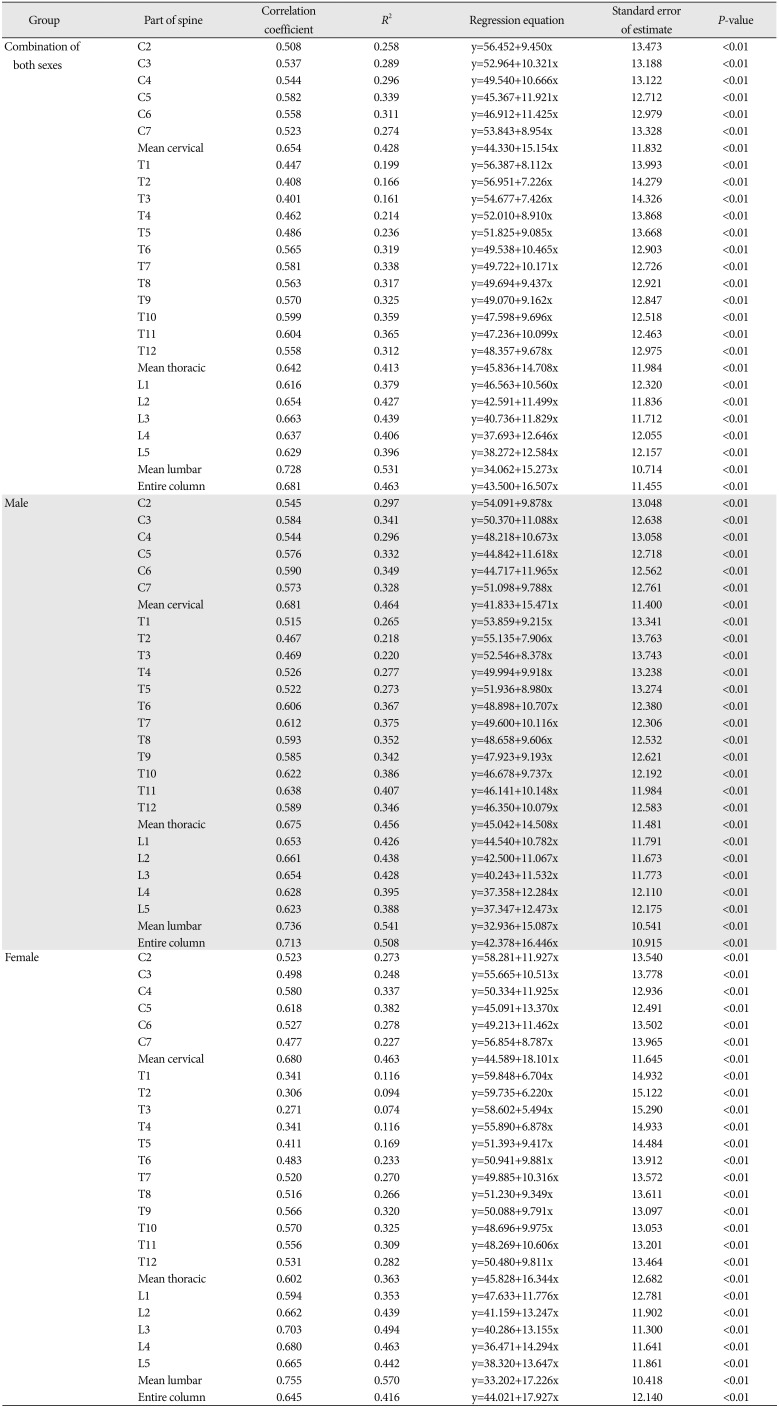
Table 2). Regression lines of criteria established by Watanabe and Terazawa (four-stage classification) were y=34.062+15.273x (SE, 10.714), y=32.936+15.087x (SE, 10.541), and y=33.202+17.226x (SE, 10.418) in mean lumbar are for combined sexes, males, and females, respectively (
Table 3). Regression lines of criteria established by new modified score by length of vertebral osteophyte (this stydy) (six-stage classification) were y=35.402+10.552x (SE, 10.369), y=34.469+10.342x (SE, 10.275), and y=34.260+12.107x (SE, 9.813) in mean lumbar area for combined sexes, males, and females, respectively (
Table 4).
Table 2
Statistical data for age (y) estimation equation from vertebral osteophytes (x) using criteria established by Snodgrass (five-stage classification) [20]
|
Group |
Part of spine |
Correlation coefficient |
R2
|
Regression equation |
Standard error of estimate |
P-value |
|
Combination of both sexes |
C2 |
0.497 |
0.230 |
y=57.608+7.735x |
13.724 |
<0.01 |
|
C3 |
0.537 |
0.288 |
y=54.382+8.283x |
13.197 |
<0.01 |
|
C4 |
0.552 |
0.305 |
y=51.239+8.223x |
13.040 |
<0.01 |
|
C5 |
0.623 |
0.388 |
y=46.399+9.094x |
12.230 |
<0.01 |
|
C6 |
0.589 |
0.346 |
y=48.383+8.541x |
12.642 |
<0.01 |
|
C7 |
0.510 |
0.260 |
y=55.166+6.902x |
13.449 |
<0.01 |
|
Mean cervical |
0.652 |
0.424 |
y=46.781+11.446x |
11.864 |
<0.01 |
|
T1 |
0.448 |
0.201 |
y=57.173+6.898x |
13.979 |
<0.01 |
|
T2 |
0.384 |
0.147 |
y=58.302+5.623x |
14.441 |
<0.01 |
|
T3 |
0.378 |
0.143 |
y=56.589+5.580x |
14.476 |
<0.01 |
|
T4 |
0.437 |
0.191 |
y=54.660+6.501x |
14.067 |
<0.01 |
|
T5 |
0.462 |
0.214 |
y=54.397+6.787x |
13.865 |
<0.01 |
|
T6 |
0.552 |
0.305 |
y=52.092+7.869x |
13.041 |
<0.01 |
|
T7 |
0.549 |
0.302 |
y=52.640+7.382x |
13.068 |
<0.01 |
|
T8 |
0.559 |
0.313 |
y=51.830+7.230x |
12.963 |
<0.01 |
|
T9 |
0.556 |
0.308 |
y=51.367+6.912x |
12.997 |
<0.01 |
|
T10 |
0.601 |
0.360 |
y=49.554+7.623x |
12.495 |
<0.01 |
|
T11 |
0.628 |
0.393 |
y=48.644+8.120x |
12.171 |
<0.01 |
|
T12 |
0.572 |
0.327 |
y=49.813+7.925x |
12.826 |
<0.01 |
|
Mean thoracic |
0.617 |
0.380 |
y=47.459+10.210x |
12.312 |
<0.01 |
|
L1 |
0.606 |
0.367 |
y=48.507+8.543x |
12.445 |
<0.01 |
|
L2 |
0.685 |
0.467 |
y=42.382+10.576x |
11.398 |
<0.01 |
|
L3 |
0.704 |
0.496 |
y=39.145+11.388x |
11.104 |
<0.01 |
|
L4 |
0.696 |
0.484 |
y=35.168+12.644x |
11.235 |
<0.01 |
|
L5 |
0.694 |
0.482 |
y=35.010+12.814x |
11.260 |
<0.01 |
|
Mean lumbar |
0.760 |
0.577 |
y=33.874+13.971x |
10.167 |
<0.01 |
|
Entire column |
0.714 |
0.509 |
y=40.783+13.373x |
10.955 |
<0.01 |
|
Male |
C2 |
0.521 |
0.271 |
y=55.475+8.016x |
13.286 |
<0.01 |
|
C3 |
0.588 |
0.346 |
y=52.073+8.782x |
12.588 |
<0.01 |
|
C4 |
0.556 |
0.309 |
y=50.006+8.235x |
12.934 |
<0.01 |
|
C5 |
0.636 |
0.405 |
y=45.037+9.165x |
12.010 |
<0.01 |
|
C6 |
0.632 |
0.399 |
y=45.701+9.040x |
12.063 |
<0.01 |
|
C7 |
0.570 |
0.325 |
y=52.469+7.586x |
12.786 |
<0.01 |
|
Mean cervical |
0.690 |
0.475 |
y=44.148+11.791x |
11.272 |
<0.01 |
|
T1 |
0.510 |
0.260 |
y=55.101+7.547x |
13.386 |
<0.01 |
|
T2 |
0.446 |
0.199 |
y=56.632+6.108x |
13.932 |
<0.01 |
|
T3 |
0.440 |
0.193 |
y=54.759+6.217x |
13.978 |
<0.01 |
|
T4 |
0.490 |
0.240 |
y=53.299+6.993x |
13.566 |
<0.01 |
|
T5 |
0.483 |
0.234 |
y=54.628+6.617x |
13.626 |
<0.01 |
|
T6 |
0.576 |
0.332 |
y=51.850+7.853x |
12.720 |
<0.01 |
|
T7 |
0.577 |
0.333 |
y=52.470+7.424x |
12.713 |
<0.01 |
|
T8 |
0.584 |
0.341 |
y=51.059+7.240x |
12.635 |
<0.01 |
|
T9 |
0.580 |
0.337 |
y=50.106+7.061x |
12.673 |
<0.01 |
|
T10 |
0.630 |
0.397 |
y=48.560+7.637x |
12.089 |
<0.01 |
|
T11 |
0.662 |
0.439 |
y=47.575+8.156x |
11.661 |
<0.01 |
|
T12 |
0.601 |
0.361 |
y=48.181+8.064x |
12.440 |
<0.01 |
|
Mean thoracic |
0.656 |
0.431 |
y=46.268+10.331x |
11.744 |
<0.01 |
|
L1 |
0.643 |
0.413 |
y=46.544+8.736x |
11.924 |
<0.01 |
|
L2 |
0.696 |
0.485 |
y=42.074+10.248x |
11.172 |
<0.01 |
|
L3 |
0.684 |
0.468 |
y=39.261+10.837x |
11.355 |
<0.01 |
|
L4 |
0.671 |
0.450 |
y=35.577+12.041x |
11.543 |
<0.01 |
|
L5 |
0.670 |
0.449 |
y=35.003+12.197x |
11.550 |
<0.01 |
|
Mean lumbar |
0.757 |
0.573 |
y=33.358+13.581x |
10.167 |
<0.01 |
|
Entire column |
0.740 |
0.548 |
y=39.539+13.230x |
10.460 |
<0.01 |
|
Female |
C2 |
0.488 |
0.238 |
y=59.162+10.305x |
13.869 |
<0.01 |
|
C3 |
0.485 |
0.235 |
y=56.822+8.701x |
13.893 |
<0.01 |
|
C4 |
0.575 |
0.330 |
y=52.317+9.001x |
13.000 |
<0.01 |
|
C5 |
0.626 |
0.391 |
y=47.622+9.636x |
12.393 |
<0.01 |
|
C6 |
0.553 |
0.306 |
y=50.878+8.818x |
13.233 |
<0.01 |
|
C7 |
0.442 |
0.195 |
y=58.255+6.695x |
14.250 |
<0.01 |
|
Mean cervical |
0.655 |
0.429 |
y=47.784+13.466x |
12.001 |
<0.01 |
|
T1 |
0.354 |
0.125 |
y=59.983+6.286x |
14.856 |
<0.01 |
|
T2 |
0.275 |
0.075 |
y=60.827+4.967x |
15.275 |
<0.01 |
|
T3 |
0.265 |
0.070 |
y=59.765+4.364x |
15.318 |
<0.01 |
|
T4 |
0.333 |
0.111 |
y=57.343+5.438x |
14.979 |
<0.01 |
|
T5 |
0.422 |
0.178 |
y=53.654+7.272x |
14.401 |
<0.01 |
|
T6 |
0.505 |
0.255 |
y=52.517+7.920x |
13.710 |
<0.01 |
|
T7 |
0.494 |
0.244 |
y=53.017+7.274x |
13.809 |
<0.01 |
|
T8 |
0.523 |
0.273 |
y=52.833+7.462x |
13.541 |
<0.01 |
|
T9 |
0.527 |
0.277 |
y=53.026+6.967x |
13.503 |
<0.01 |
|
T10 |
0.564 |
0.318 |
y=50.608+8.015x |
13.119 |
<0.01 |
|
T11 |
0.578 |
0.335 |
y=49.816+8.479x |
12.958 |
<0.01 |
|
T12 |
0.553 |
0.306 |
y=51.149+8.593x |
13.237 |
<0.01 |
|
Mean thoracic |
0.555 |
0.307 |
y=48.880+10.451x |
13.219 |
<0.01 |
|
L1 |
0.580 |
0.337 |
y=49.850+9.441x |
12.938 |
<0.01 |
|
L2 |
0.687 |
0.472 |
y=41.411+12.018x |
11.544 |
<0.01 |
|
L3 |
0.772 |
0.595 |
y=37.251+13.323x |
10.106 |
<0.01 |
|
L4 |
0.764 |
0.584 |
y=32.961+14.514x |
10.240 |
<0.01 |
|
L5 |
0.746 |
0.557 |
y=34.580+13.640x |
10.579 |
<0.01 |
|
Mean lumbar |
0.801 |
0.642 |
y=32.308+15.994x |
9.506 |
<0.01 |
|
Entire column |
0.705 |
0.497 |
y=40.324+15.350x |
11.264 |
<0.01 |

Table 3
Statistical data for age (y) estimation equation from vertebral osteophytes (x) using criteria established by Watanabe and Terazawa (four-stage classification) [15]
|
Group |
Part of spine |
Correlation coefficient |
R2
|
Regression equation |
Standard error of estimate |
P-value |
|
Combination of both sexes |
C2 |
0.508 |
0.258 |
y=56.452+9.450x |
13.473 |
<0.01 |
|
C3 |
0.537 |
0.289 |
y=52.964+10.321x |
13.188 |
<0.01 |
|
C4 |
0.544 |
0.296 |
y=49.540+10.666x |
13.122 |
<0.01 |
|
C5 |
0.582 |
0.339 |
y=45.367+11.921x |
12.712 |
<0.01 |
|
C6 |
0.558 |
0.311 |
y=46.912+11.425x |
12.979 |
<0.01 |
|
C7 |
0.523 |
0.274 |
y=53.843+8.954x |
13.328 |
<0.01 |
|
Mean cervical |
0.654 |
0.428 |
y=44.330+15.154x |
11.832 |
<0.01 |
|
T1 |
0.447 |
0.199 |
y=56.387+8.112x |
13.993 |
<0.01 |
|
T2 |
0.408 |
0.166 |
y=56.951+7.226x |
14.279 |
<0.01 |
|
T3 |
0.401 |
0.161 |
y=54.677+7.426x |
14.326 |
<0.01 |
|
T4 |
0.462 |
0.214 |
y=52.010+8.910x |
13.868 |
<0.01 |
|
T5 |
0.486 |
0.236 |
y=51.825+9.085x |
13.668 |
<0.01 |
|
T6 |
0.565 |
0.319 |
y=49.538+10.465x |
12.903 |
<0.01 |
|
T7 |
0.581 |
0.338 |
y=49.722+10.171x |
12.726 |
<0.01 |
|
T8 |
0.563 |
0.317 |
y=49.694+9.437x |
12.921 |
<0.01 |
|
T9 |
0.570 |
0.325 |
y=49.070+9.162x |
12.847 |
<0.01 |
|
T10 |
0.599 |
0.359 |
y=47.598+9.696x |
12.518 |
<0.01 |
|
T11 |
0.604 |
0.365 |
y=47.236+10.099x |
12.463 |
<0.01 |
|
T12 |
0.558 |
0.312 |
y=48.357+9.678x |
12.975 |
<0.01 |
|
Mean thoracic |
0.642 |
0.413 |
y=45.836+14.708x |
11.984 |
<0.01 |
|
L1 |
0.616 |
0.379 |
y=46.563+10.560x |
12.320 |
<0.01 |
|
L2 |
0.654 |
0.427 |
y=42.591+11.499x |
11.836 |
<0.01 |
|
L3 |
0.663 |
0.439 |
y=40.736+11.829x |
11.712 |
<0.01 |
|
L4 |
0.637 |
0.406 |
y=37.693+12.646x |
12.055 |
<0.01 |
|
L5 |
0.629 |
0.396 |
y=38.272+12.584x |
12.157 |
<0.01 |
|
Mean lumbar |
0.728 |
0.531 |
y=34.062+15.273x |
10.714 |
<0.01 |
|
Entire column |
0.681 |
0.463 |
y=43.500+16.507x |
11.455 |
<0.01 |
|
Male |
C2 |
0.545 |
0.297 |
y=54.091+9.878x |
13.048 |
<0.01 |
|
C3 |
0.584 |
0.341 |
y=50.370+11.088x |
12.638 |
<0.01 |
|
C4 |
0.544 |
0.296 |
y=48.218+10.673x |
13.058 |
<0.01 |
|
C5 |
0.576 |
0.332 |
y=44.842+11.618x |
12.718 |
<0.01 |
|
C6 |
0.590 |
0.349 |
y=44.717+11.965x |
12.562 |
<0.01 |
|
C7 |
0.573 |
0.328 |
y=51.098+9.788x |
12.761 |
<0.01 |
|
Mean cervical |
0.681 |
0.464 |
y=41.833+15.471x |
11.400 |
<0.01 |
|
T1 |
0.515 |
0.265 |
y=53.859+9.215x |
13.341 |
<0.01 |
|
T2 |
0.467 |
0.218 |
y=55.135+7.906x |
13.763 |
<0.01 |
|
T3 |
0.469 |
0.220 |
y=52.546+8.378x |
13.743 |
<0.01 |
|
T4 |
0.526 |
0.277 |
y=49.994+9.918x |
13.238 |
<0.01 |
|
T5 |
0.522 |
0.273 |
y=51.936+8.980x |
13.274 |
<0.01 |
|
T6 |
0.606 |
0.367 |
y=48.898+10.707x |
12.380 |
<0.01 |
|
T7 |
0.612 |
0.375 |
y=49.600+10.116x |
12.306 |
<0.01 |
|
T8 |
0.593 |
0.352 |
y=48.658+9.606x |
12.532 |
<0.01 |
|
T9 |
0.585 |
0.342 |
y=47.923+9.193x |
12.621 |
<0.01 |
|
T10 |
0.622 |
0.386 |
y=46.678+9.737x |
12.192 |
<0.01 |
|
T11 |
0.638 |
0.407 |
y=46.141+10.148x |
11.984 |
<0.01 |
|
T12 |
0.589 |
0.346 |
y=46.350+10.079x |
12.583 |
<0.01 |
|
Mean thoracic |
0.675 |
0.456 |
y=45.042+14.508x |
11.481 |
<0.01 |
|
L1 |
0.653 |
0.426 |
y=44.540+10.782x |
11.791 |
<0.01 |
|
L2 |
0.661 |
0.438 |
y=42.500+11.067x |
11.673 |
<0.01 |
|
L3 |
0.654 |
0.428 |
y=40.243+11.532x |
11.773 |
<0.01 |
|
L4 |
0.628 |
0.395 |
y=37.358+12.284x |
12.110 |
<0.01 |
|
L5 |
0.623 |
0.388 |
y=37.347+12.473x |
12.175 |
<0.01 |
|
Mean lumbar |
0.736 |
0.541 |
y=32.936+15.087x |
10.541 |
<0.01 |
|
Entire column |
0.713 |
0.508 |
y=42.378+16.446x |
10.915 |
<0.01 |
|
Female |
C2 |
0.523 |
0.273 |
y=58.281+11.927x |
13.540 |
<0.01 |
|
C3 |
0.498 |
0.248 |
y=55.665+10.513x |
13.778 |
<0.01 |
|
C4 |
0.580 |
0.337 |
y=50.334+11.925x |
12.936 |
<0.01 |
|
C5 |
0.618 |
0.382 |
y=45.091+13.370x |
12.491 |
<0.01 |
|
C6 |
0.527 |
0.278 |
y=49.213+11.462x |
13.502 |
<0.01 |
|
C7 |
0.477 |
0.227 |
y=56.854+8.787x |
13.965 |
<0.01 |
|
Mean cervical |
0.680 |
0.463 |
y=44.589+18.101x |
11.645 |
<0.01 |
|
T1 |
0.341 |
0.116 |
y=59.848+6.704x |
14.932 |
<0.01 |
|
T2 |
0.306 |
0.094 |
y=59.735+6.220x |
15.122 |
<0.01 |
|
T3 |
0.271 |
0.074 |
y=58.602+5.494x |
15.290 |
<0.01 |
|
T4 |
0.341 |
0.116 |
y=55.890+6.878x |
14.933 |
<0.01 |
|
T5 |
0.411 |
0.169 |
y=51.393+9.417x |
14.484 |
<0.01 |
|
T6 |
0.483 |
0.233 |
y=50.941+9.881x |
13.912 |
<0.01 |
|
T7 |
0.520 |
0.270 |
y=49.885+10.316x |
13.572 |
<0.01 |
|
T8 |
0.516 |
0.266 |
y=51.230+9.349x |
13.611 |
<0.01 |
|
T9 |
0.566 |
0.320 |
y=50.088+9.791x |
13.097 |
<0.01 |
|
T10 |
0.570 |
0.325 |
y=48.696+9.975x |
13.053 |
<0.01 |
|
T11 |
0.556 |
0.309 |
y=48.269+10.606x |
13.201 |
<0.01 |
|
T12 |
0.531 |
0.282 |
y=50.480+9.811x |
13.464 |
<0.01 |
|
Mean thoracic |
0.602 |
0.363 |
y=45.828+16.344x |
12.682 |
<0.01 |
|
L1 |
0.594 |
0.353 |
y=47.633+11.776x |
12.781 |
<0.01 |
|
L2 |
0.662 |
0.439 |
y=41.159+13.247x |
11.902 |
<0.01 |
|
L3 |
0.703 |
0.494 |
y=40.286+13.155x |
11.300 |
<0.01 |
|
L4 |
0.680 |
0.463 |
y=36.471+14.294x |
11.641 |
<0.01 |
|
L5 |
0.665 |
0.442 |
y=38.320+13.647x |
11.861 |
<0.01 |
|
Mean lumbar |
0.755 |
0.570 |
y=33.202+17.226x |
10.418 |
<0.01 |
|
Entire column |
0.645 |
0.416 |
y=44.021+17.927x |
12.14 |
<0.01 |

Table 4
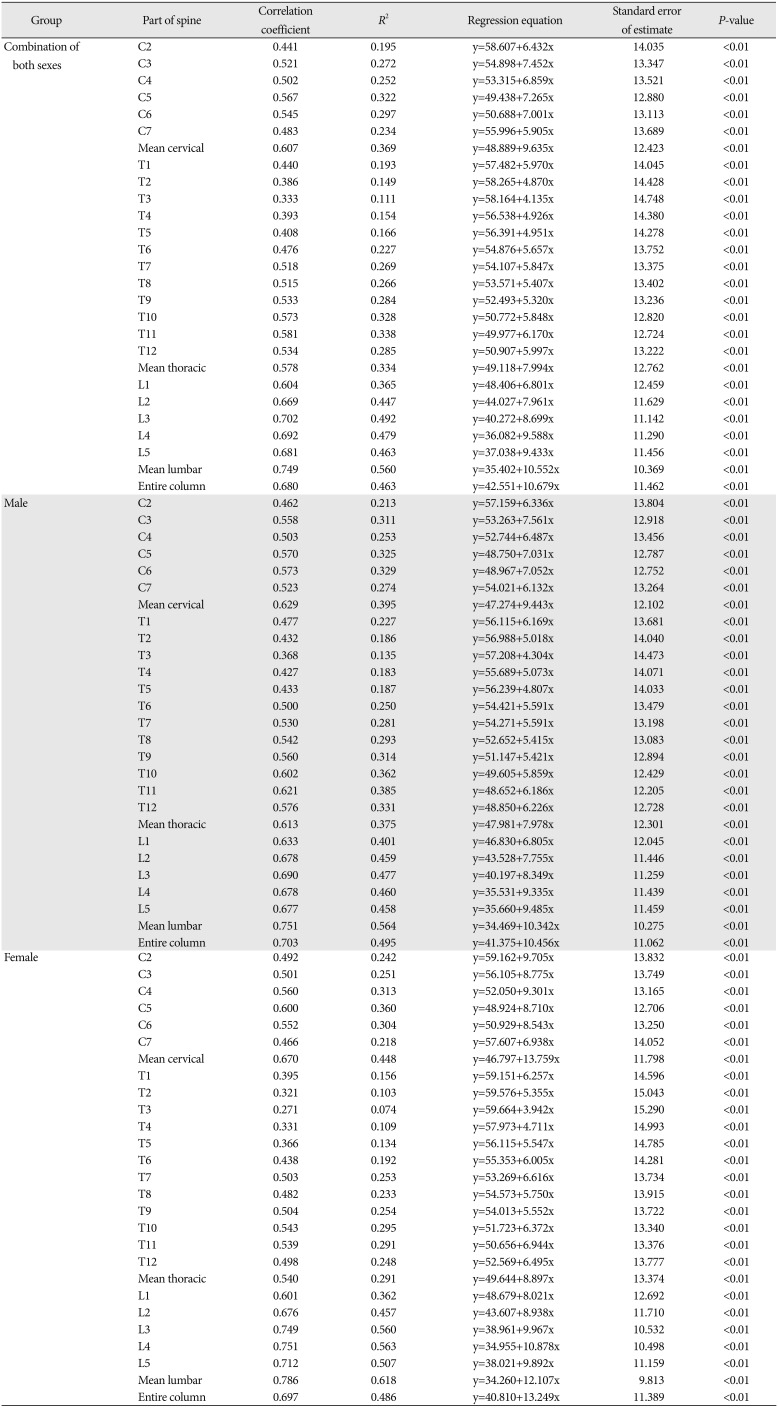
Statistical data for age (y) estimation equation from vertebral osteophytes (x) using criteria established by new modified score by length of vertebral osteophyte (this study) (six-stage classification)
|
Group |
Part of spine |
Correlation coefficient |
R2
|
Regression equation |
Standard error of estimate |
P-value |
|
Combination of both sexes |
C2 |
0.441 |
0.195 |
y=58.607+6.432x |
14.035 |
<0.01 |
|
C3 |
0.521 |
0.272 |
y=54.898+7.452x |
13.347 |
<0.01 |
|
C4 |
0.502 |
0.252 |
y=53.315+6.859x |
13.521 |
<0.01 |
|
C5 |
0.567 |
0.322 |
y=49.438+7.265x |
12.880 |
<0.01 |
|
C6 |
0.545 |
0.297 |
y=50.688+7.001x |
13.113 |
<0.01 |
|
C7 |
0.483 |
0.234 |
y=55.996+5.905x |
13.689 |
<0.01 |
|
Mean cervical |
0.607 |
0.369 |
y=48.889+9.635x |
12.423 |
<0.01 |
|
T1 |
0.440 |
0.193 |
y=57.482+5.970x |
14.045 |
<0.01 |
|
T2 |
0.386 |
0.149 |
y=58.265+4.870x |
14.428 |
<0.01 |
|
T3 |
0.333 |
0.111 |
y=58.164+4.135x |
14.748 |
<0.01 |
|
T4 |
0.393 |
0.154 |
y=56.538+4.926x |
14.380 |
<0.01 |
|
T5 |
0.408 |
0.166 |
y=56.391+4.951x |
14.278 |
<0.01 |
|
T6 |
0.476 |
0.227 |
y=54.876+5.657x |
13.752 |
<0.01 |
|
T7 |
0.518 |
0.269 |
y=54.107+5.847x |
13.375 |
<0.01 |
|
T8 |
0.515 |
0.266 |
y=53.571+5.407x |
13.402 |
<0.01 |
|
T9 |
0.533 |
0.284 |
y=52.493+5.320x |
13.236 |
<0.01 |
|
T10 |
0.573 |
0.328 |
y=50.772+5.848x |
12.820 |
<0.01 |
|
T11 |
0.581 |
0.338 |
y=49.977+6.170x |
12.724 |
<0.01 |
|
T12 |
0.534 |
0.285 |
y=50.907+5.997x |
13.222 |
<0.01 |
|
Mean thoracic |
0.578 |
0.334 |
y=49.118+7.994x |
12.762 |
<0.01 |
|
L1 |
0.604 |
0.365 |
y=48.406+6.801x |
12.459 |
<0.01 |
|
L2 |
0.669 |
0.447 |
y=44.027+7.961x |
11.629 |
<0.01 |
|
L3 |
0.702 |
0.492 |
y=40.272+8.699x |
11.142 |
<0.01 |
|
L4 |
0.692 |
0.479 |
y=36.082+9.588x |
11.290 |
<0.01 |
|
L5 |
0.681 |
0.463 |
y=37.038+9.433x |
11.456 |
<0.01 |
|
Mean lumbar |
0.749 |
0.560 |
y=35.402+10.552x |
10.369 |
<0.01 |
|
Entire column |
0.680 |
0.463 |
y=42.551+10.679x |
11.462 |
<0.01 |
|
Male |
C2 |
0.462 |
0.213 |
y=57.159+6.336x |
13.804 |
<0.01 |
|
C3 |
0.558 |
0.311 |
y=53.263+7.561x |
12.918 |
<0.01 |
|
C4 |
0.503 |
0.253 |
y=52.744+6.487x |
13.456 |
<0.01 |
|
C5 |
0.570 |
0.325 |
y=48.750+7.031x |
12.787 |
<0.01 |
|
C6 |
0.573 |
0.329 |
y=48.967+7.052x |
12.752 |
<0.01 |
|
C7 |
0.523 |
0.274 |
y=54.021+6.132x |
13.264 |
<0.01 |
|
Mean cervical |
0.629 |
0.395 |
y=47.274+9.443x |
12.102 |
<0.01 |
|
T1 |
0.477 |
0.227 |
y=56.115+6.169x |
13.681 |
<0.01 |
|
T2 |
0.432 |
0.186 |
y=56.988+5.018x |
14.040 |
<0.01 |
|
T3 |
0.368 |
0.135 |
y=57.208+4.304x |
14.473 |
<0.01 |
|
T4 |
0.427 |
0.183 |
y=55.689+5.073x |
14.071 |
<0.01 |
|
T5 |
0.433 |
0.187 |
y=56.239+4.807x |
14.033 |
<0.01 |
|
T6 |
0.500 |
0.250 |
y=54.421+5.591x |
13.479 |
<0.01 |
|
T7 |
0.530 |
0.281 |
y=54.271+5.591x |
13.198 |
<0.01 |
|
T8 |
0.542 |
0.293 |
y=52.652+5.415x |
13.083 |
<0.01 |
|
T9 |
0.560 |
0.314 |
y=51.147+5.421x |
12.894 |
<0.01 |
|
T10 |
0.602 |
0.362 |
y=49.605+5.859x |
12.429 |
<0.01 |
|
T11 |
0.621 |
0.385 |
y=48.652+6.186x |
12.205 |
<0.01 |
|
T12 |
0.576 |
0.331 |
y=48.850+6.226x |
12.728 |
<0.01 |
|
Mean thoracic |
0.613 |
0.375 |
y=47.981+7.978x |
12.301 |
<0.01 |
|
L1 |
0.633 |
0.401 |
y=46.830+6.805x |
12.045 |
<0.01 |
|
L2 |
0.678 |
0.459 |
y=43.528+7.755x |
11.446 |
<0.01 |
|
L3 |
0.690 |
0.477 |
y=40.197+8.349x |
11.259 |
<0.01 |
|
L4 |
0.678 |
0.460 |
y=35.531+9.335x |
11.439 |
<0.01 |
|
L5 |
0.677 |
0.458 |
y=35.660+9.485x |
11.459 |
<0.01 |
|
Mean lumbar |
0.751 |
0.564 |
y=34.469+10.342x |
10.275 |
<0.01 |
|
Entire column |
0.703 |
0.495 |
y=41.375+10.456x |
11.062 |
<0.01 |
|
Female |
C2 |
0.492 |
0.242 |
y=59.162+9.705x |
13.832 |
<0.01 |
|
C3 |
0.501 |
0.251 |
y=56.105+8.775x |
13.749 |
<0.01 |
|
C4 |
0.560 |
0.313 |
y=52.050+9.301x |
13.165 |
<0.01 |
|
C5 |
0.600 |
0.360 |
y=48.924+8.710x |
12.706 |
<0.01 |
|
C6 |
0.552 |
0.304 |
y=50.929+8.543x |
13.250 |
<0.01 |
|
C7 |
0.466 |
0.218 |
y=57.607+6.938x |
14.052 |
<0.01 |
|
Mean cervical |
0.670 |
0.448 |
y=46.797+13.759x |
11.798 |
<0.01 |
|
T1 |
0.395 |
0.156 |
y=59.151+6.257x |
14.596 |
<0.01 |
|
T2 |
0.321 |
0.103 |
y=59.576+5.355x |
15.043 |
<0.01 |
|
T3 |
0.271 |
0.074 |
y=59.664+3.942x |
15.290 |
<0.01 |
|
T4 |
0.331 |
0.109 |
y=57.973+4.711x |
14.993 |
<0.01 |
|
T5 |
0.366 |
0.134 |
y=56.115+5.547x |
14.785 |
<0.01 |
|
T6 |
0.438 |
0.192 |
y=55.353+6.005x |
14.281 |
<0.01 |
|
T7 |
0.503 |
0.253 |
y=53.269+6.616x |
13.734 |
<0.01 |
|
T8 |
0.482 |
0.233 |
y=54.573+5.750x |
13.915 |
<0.01 |
|
T9 |
0.504 |
0.254 |
y=54.013+5.552x |
13.722 |
<0.01 |
|
T10 |
0.543 |
0.295 |
y=51.723+6.372x |
13.340 |
<0.01 |
|
T11 |
0.539 |
0.291 |
y=50.656+6.944x |
13.376 |
<0.01 |
|
T12 |
0.498 |
0.248 |
y=52.569+6.495x |
13.777 |
<0.01 |
|
Mean thoracic |
0.540 |
0.291 |
y=49.644+8.897x |
13.374 |
<0.01 |
|
L1 |
0.601 |
0.362 |
y=48.679+8.021x |
12.692 |
<0.01 |
|
L2 |
0.676 |
0.457 |
y=43.607+8.938x |
11.710 |
<0.01 |
|
L3 |
0.749 |
0.560 |
y=38.961+9.967x |
10.532 |
<0.01 |
|
L4 |
0.751 |
0.563 |
y=34.955+10.878x |
10.498 |
<0.01 |
|
L5 |
0.712 |
0.507 |
y=38.021+9.892x |
11.159 |
<0.01 |
|
Mean lumbar |
0.786 |
0.618 |
y=34.260+12.107x |
9.813 |
<0.01 |
|
Entire column |
0.697 |
0.486 |
y=40.810+13.249x |
11.389 |
<0.01 |

Correlation coefficients of criteria established by the method of Snodgrass [
14] were as follows: 0.378<
r<0.76,
P<0.01; 0.44<
r<0.757,
P<0.01; and 0.265<
r<0.801,
P<0.01 for a combination of the sexes, males, and females, respectively. Correlation coefficients of criteria established by the method of Watanabe and colleagues were as follows: 0.401<
r<0.728,
P<0.01; 0.467<
r<0.736,
P<0.01; and 0.271<
r<0.755,
P<0.01 for a combination of the sexes, males, and females, respectively. Correlation coefficients of criteria established by the method of Praneatpolgrang and colleagues were as follows: 0.333<
r<0.749,
P<0.01; 0.368<
r<0.751,
P<0.01; and 0.271<
r<0.786,
P<0.01 for a combination of the sexes, males, and females, respectively.
Go to :

Discussion
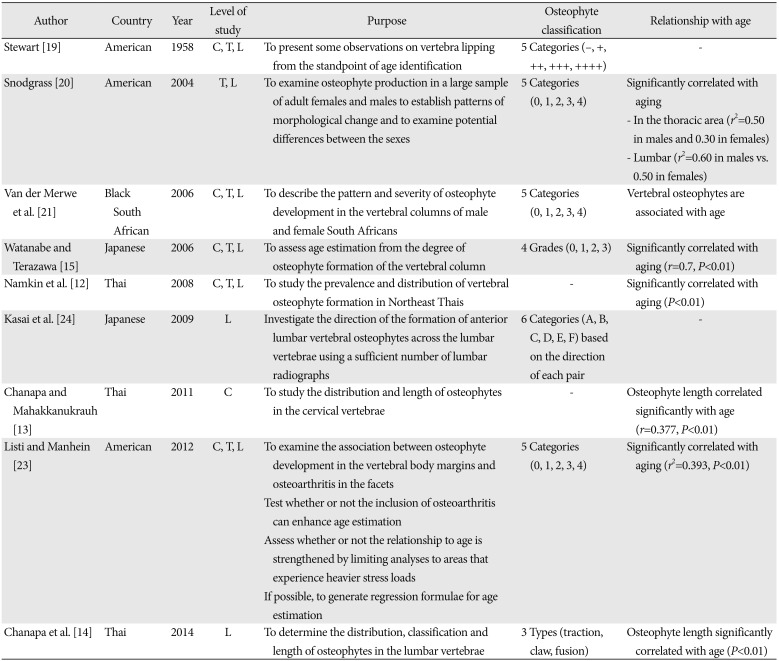
In the past there have been several studies into vertebral osteophyte formation (
Table 5). Many researchers have reported many corresponding findings [
121314151920212324] on osteophyte formation and age, showing statistically significant correlations. But no relationship had been published for its use in age estimation until Watanabe and Terazawa [
15] and Listi and Manhein [
23] tried to conduct research into age estimation in relation to osteophyte formation. Watanabe went on to create an equation to estimate the age [
15].
Table 5
A summary of studies into vertebral osteophyte formation
|
Author |
Country |
Year |
Level of study |
Purpose |
Osteophyte classification |
Relationship with age |
|
Stewart [19] |
American |
1958 |
C, T, L |
To present some observations on vertebra lipping from the standpoint of age identification |
5 Categories (−, +, ++, +++, ++++) |
- |
|
Snodgrass [20] |
American |
2004 |
T, L |
To examine osteophyte production in a large sample of adult females and males to establish patterns of morphological change and to examine potential differences between the sexes |
5 Categories (0, 1, 2, 3, 4) |
Significantly correlated with aging |
|
- In the thoracic area (r2=0.50 in males and 0.30 in females) |
|
- Lumbar (r2=0.60 in males vs. 0.50 in females) |
|
Van der Merwe et al. [21] |
Black South African |
2006 |
C, T, L |
To describe the pattern and severity of osteophyte development in the vertebral columns of male and female South Africans |
5 Categories (0, 1, 2, 3, 4) |
Vertebral osteophytes are associated with age |
|
Watanabe and Terazawa [15] |
Japanese |
2006 |
C, T, L |
To assess age estimation from the degree of osteophyte formation of the vertebral column |
4 Grades (0, 1, 2, 3) |
Significantly correlated with aging (r=0.7, P<0.01) |
|
Namkin et al. [12] |
Thai |
2008 |
C, T, L |
To study the prevalence and distribution of vertebral osteophyte formation in Northeast Thais |
- |
Significantly correlated with aging (P<0.01) |
|
Kasai et al. [24] |
Japanese |
2009 |
L |
Investigate the direction of the formation of anterior lumbar vertebral osteophytes across the lumbar vertebrae using a sufficient number of lumbar radiographs |
6 Categories (A, B, C, D, E, F) based on the direction of each pair |
- |
|
Chanapa and Mahakkanukrauh [13] |
Thai |
2011 |
C |
To study the distribution and length of osteophytes in the cervical vertebrae |
- |
Osteophyte length correlated significantly with age (r=0.377, P<0.01) |
|
Listi and Manhein [23] |
American |
2012 |
C, T, L |
To examine the association between osteophyte development in the vertebral body margins and osteoarthritis in the facets Test whether or not the inclusion of osteoarthritis can enhance age estimation Assess whether or not the relationship to age is strengthened by limiting analyses to areas that experience heavier stress loads If possible, to generate regression formulae for age estimation |
5 Categories (0, 1, 2, 3, 4) |
Significantly correlated with aging (r2=0.393, P<0.01) |
|
Chanapa et al. [14] |
Thai |
2014 |
L |
To determine the distribution, classification and length of osteophytes in the lumbar vertebrae |
3 Types (traction, claw, fusion) |
Osteophyte length significantly correlated with age (P<0.01) |

The current study used a scoring method based on Snodgrass [
20] and Watanabe and Terazawa [
15]. The two previous scoring methods are used because both of these methods have been published for use in estimating age. Earlier studies have provided a wide variety of scoring methods. But there are no studies that can be used to estimate an age equation.
Watanabe was a study that could produce an equations for age. It was a new method of scoring based on the height of the osteophyte, but the range is still wide.
This study presents all 23 subcategories (C2–L5) of the vertebrae and shows all three scoring methods of the different processes from previous studies for age estimation equations for males, females and combined sexes of unknown sex, in order to be useful to readers and be applied in real situations. Also, these findings need to be used in accordance with the situations that occur around skeletal remains in order to help identity them.
In this study, analysis of the scoring for the degree of osteophyte formation using the three different criteria (Snodgrass, Watanabe, and Praneatpolgrang [this study]) resulted in no difference between the correlation coefficients. In comparing the correlation coefficient and
R2 values of the three scoring methods (Snodgrass, Watanabe, and Praneatpolgrang), we attempted to find out which of the three ways was best. The results indicate that all three ways are similar, showing that the three scores for degree of osteophyte formation in females was not significantly different and had a correlation coefficient of 0.801 (
Table 2) using the Snodgrass [
20] (five-stage classification) criteria. Snodgrass' scoring criteria was better than the other two scoring criteria (correlation coefficients of Snodgrass criteria were 0.76, 0.757, and 0.801 for a combination of the sexes, males, and females, respectively). This study used a new modified score by the length of vertebral osteophyte (
Tables 1,
4). The new modified score measurement is more objective than the others because it provides a more frequent scoring range, which is clearer by the length of the osteophyte and makes the scoring faster by using a digital vernier caliper and measuring tape, which can be seen clearly and more objectively. Correlation coefficients of the Praneatpolgrang criteria were as follows: 0.749, 0.751, and 0.786 for a combination of the sexes, males, and females, respectively, and correlation coefficients of Praneatpolgrang's scoring criteria were considered to have high correlation [
25]. All three scoring methods could be practically used because they had relatively high correlation with age [
25].
The advantage of this research is that all three scoring criteria of different processes from previous studies for age estimation equations for males, females, and combined sexes are simple, easy to use, inexpensive and fast methods for estimating the age of a skeleton. Snodgrass' study (2004) [
20] cannot create an age estimation equation, possibly due to a different process. The current study's preliminary results show the possibility of using vertebral osteophytes for age-at-death estimation in the Thai population.
The entire spinal columns and each subcategory of vertebrae were scored for the degree of osteophyte formation according to criteria established by Snodgrass [
20] (five-stage classification), Watanabe and Terazawa [
15] (four-stage classification), and the new modified score using the length of vertebral osteophyte method (this study) (six-stage classification). The report includes all age equations for an entire column and each subcategory of vertebrae (
Tables 2,
3,
4) for three criteria of scores to determine the degree of osteophyte formation. Some sections showed a low correlation but the authors see that as a useful finding for further investigation. Also these findings need to be used in accordance with the situation that occurs around each skeletal remains in order to help identity them. This includes cases where all vertebrae are found, in which case the highest correlation coefficient and R
2 values should be sought. If only a few vertebrae are discovered this method should probably not be used.
The current study has been developed for three scoring methods and providesa more frequent scoring range using Praneatpolgrang's scoring. The new modified score measurement is clearer by the length of the osteophyte. It uses a larger reference sample from 400 individuals. This study can add weight to the findings from investigations of age estimation in the Thai population and can be useful in the field when dealing with forensic cases.
Go to :











 PDF
PDF ePub
ePub Citation
Citation Print
Print



 XML Download
XML Download