High-Resolution Numerical Simulation of Respiration-Induced Dynamic B0 Shift in the Head in High-Field MRI

So-Hee Lee; Ji-Seong Barg; Seok-Jin Yeo; Seung-Kyun Lee

doi:10.13104/imri.2019.23.1.38

Journal List > Investig Magn Reson Imaging > v.23(1) > 1125200

Go to TopGo to Top Go to BottomGo to Bottom

TOOLS

Lee, Barg, Yeo, and Lee: High-Resolution Numerical Simulation of Respiration-Induced Dynamic B0 Shift in the Head in High-Field MRI

Original Article

iMRI 2019;23(1):38-45.

Published online: 10 January 2019

DOI: https://doi.org/10.13104/imri.2019.23.1.38

High-Resolution Numerical Simulation of Respiration-Induced Dynamic B₀ Shift in the Head in High-Field MRI

So-Hee Lee^1,², Ji-Seong Barg^1,², Seok-Jin Yeo^1,², Seung-Kyun Lee^1,²

¹Center for Neuroscience Imaging Research, Institute for Basic Science (IBS), Suwon, Korea

²Department of Biomedical Engineering, Sungkyunkwan University, Suwon, Korea

Correspondence to: Seung-Kyun Lee, Ph.D. Center for Neuroscience Imaging Research, Department of Biomedical Engineering, Sungkyunkwan University, 2066 Seobu-ro, Jangan-gu, Suwon-si, Gyeonggi-do 16419, Korea. Tel. +82-31-299-4401 Fax. +82-31-299-4506 E-mail: seungkyun@skku.edu

Received 29 August 2018 Revised 29 November 2018 Accepted 1 February 2019

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

Purpose

To demonstrate the high-resolution numerical simulation of the respiration-induced dynamic B₀ shift in the head using generalized susceptibility voxel convolution (gSVC).

Materials and Methods

Previous dynamic B₀ simulation research has been limited to low-resolution numerical models due to the large computational demands of conventional Fourier-based B₀ calculation methods. Here, we show that a recently-proposed gSVC method can simulate dynamic B₀ maps from a realistic breathing human body model with high spatiotemporal resolution in a time-efficient manner. For a human body model, we used the Extended Cardiac And Torso (XCAT) phantom originally developed for computed tomography. The spatial resolution (voxel size) was kept isotropic and varied from 1 to 10 mm. We calculated B₀ maps in the brain of the model at 10 equally spaced points in a respiration cycle and analyzed the spatial gradients of each of them. The results were compared with experimental measurements in the literature.

Results

The simulation predicted a maximum temporal variation of the B₀ shift in the brain of about 7 Hz at 7T. The magnitudes of the respiration-induced B₀ gradient in the x (right/left), y (anterior/posterior), and z (head/feet) directions determined by volumetric linear fitting, were < 0.01 Hz/cm, 0.18 Hz/cm, and 0.26 Hz/cm, respectively. These compared favorably with previous reports. We found that simulation voxel sizes greater than 5 mm can produce unreliable results.

Conclusion

We have presented an efficient simulation framework for respiration-induced B₀ variation in the head. The method can be used to predict B₀ shifts with high spatiotemporal resolution under different breathing conditions and aid in the design of dynamic B₀ compensation strategies.

Keywords: Dynamic B₀ shift, Dynamic shim, Respiration, Susceptibility, Brain, 7T

References

1. Koch KM, Rothman DL, de Graaf RA. Optimization of static magnetic field homogeneity in the human and animal brain in vivo. Prog Nucl Magn Reson Spectrosc. 2009; 54:69–96.

2. Kim PK, Lim JW, Ahn CB. Higher order shimming for ultrafast spiral-scan imaging at 3 tesla MRI system. J Korean Soc Magn Reson Med. 2007; 11:95–102.

3. Foerster BU, Tomasi D, Caparelli EC. Magnetic field shift due to mechanical vibration in functional magnetic resonance imaging. Magn Reson Med. 2005; 54:1261–1267.

4. Hutton C, Andersson J, Deichmann R, Weiskopf N. Phase informed model for motion and susceptibility. Hum Brain Mapp. 2013; 34:3086–3100.

5. Bouwman JG, Bakker CJ. Alias subtraction more efficient than conventional zero-padding in the Fourier-based calculation of the susceptibility induced perturbation of the magnetic field in MR. Magn Reson Med. 2012; 68:621–630.

6. Zahneisen B, Asslander J, LeVan P, et al. Quantification and correction of respiration induced dynamic field map changes in fMRI using 3D single shot techniques. Magn Reson Med. 2014; 71:1093–1102.

7. Zeller M, Kraus P, Muller A, Bley TA, Kostler H. Respiration impacts phase difference-based field maps in echo planar imaging. Magn Reson Med. 2014; 72:446–451.

8. Van de Moortele PF, Pfeuffer J, Glover GH, Ugurbil K, Hu X. Respiration-induced B₀ fluctuations and their spatial distribution in the human brain at 7 Tesla. Magn Reson Med. 2002; 47:888–895.

9. Vannesjo SJ, Wilm BJ, Duerst Y, et al. Retrospective correction of physiological field fluctuations in high-field brain MRI using concurrent field monitoring. Magn Reson Med. 2015; 73:1833–1843.

10. Meineke J, Nielsen T. Data-driven correction of B₀-off-resonance fluctuations in gradient-echo MRI. In Proceedings of the 26th Annual Meeting of ISMRM. Paris, France. 2018. 1172.

11. Marques JP, Bowtell R. Application of a Fourier-based method for rapid calculation of field inhomogeneity due to spatial variation of magnetic susceptibility. Concepts Magn Reson Part B. 2005; 25B:65–78.

12. Lee SK, Hwang SH, Barg JS, Yeo SJ. Rapid, theoretically artifact-free calculation of static magnetic field induced by voxelated susceptibility distribution in an arbitrary volume of interest. Magn Reson Med. 2018; 80:2109–2121.

13. Segars WP, Mahesh M, Beck TJ, Frey EC, Tsui BM. Realistic CT simulation using the 4D XCAT phantom. Med Phys. 2008; 35:3800–3808.

14. Silva-Rodriguez J, Tsoumpas C, Dominguez-Prado I, Pardo-Montero J, Ruibal A, Aguiar P. Impact and correction of the bladder uptake on 18 F-FCH PET quantification: a simulation study using the XCAT2 phantom. Phys Med Biol. 2016; 61:758–773.

15. Koybasi O, Mishra P, St James S, Lewis JH, Seco J. Simulation of dosimetric consequences of 4D-CT-based motion margin estimation for proton radiotherapy using patient tumor motion data. Phys Med Biol. 2014; 59:853–867.

16. Lowther N, Ipsen S, Marsh S, Blanck O, Keall P. Investigation of the XCAT phantom as a validation tool in cardiac MRI tracking algorithms. Phys Med. 2018; 45:44–51.

17. Paganelli C, Summers P, Gianoli C, Bellomi M, Baroni G, Riboldi M. A tool for validating MRI-guided strategies: a digital breathing CT/MRI phantom of the abdominal site. Med Biol Eng Comput. 2017; 55:2001–2014.

18. Dewal RP, Yang QX. Volume of interest-based fourier transform method for calculation of static magnetic field maps from susceptibility distributions. Magn Reson Med. 2016; 75:2473–2480.

19. Raj D, Paley DP, Anderson AW, Kennan RP, Gore JC. A model for susceptibility artefacts from respiration in functional echoplanar magnetic resonance imaging. Phys Med Biol. 2000; 45:3809–3820.

20. Lee SK, Barg JS, Yeo SJ. Respiration-induced dynamic B₀ shifts in the head: numerical simulation based on generalized susceptibility voxel convolution (gSVC). The 6th International Congress on Magnetic Resonance Imaging (ICMRI). Seoul, Korea. 2018.

Fig. 1.

Sagittal cross sections of the brain mask (dotted line) and the susceptibility model at voxel sizes of 0.1 cm (a) and 0.7 cm (b). Tick mark labels indicate voxels. For each voxel size, frames 1 (left) and 5 (right) are displayed out of the 10 frames in the breathing cycle simulated by the 4D XCAT model. Color bar at the bottom indicates susceptibility in ppm (0 = air and lung, −8.5 = blood, −9 = other tissue, −11 = bone).

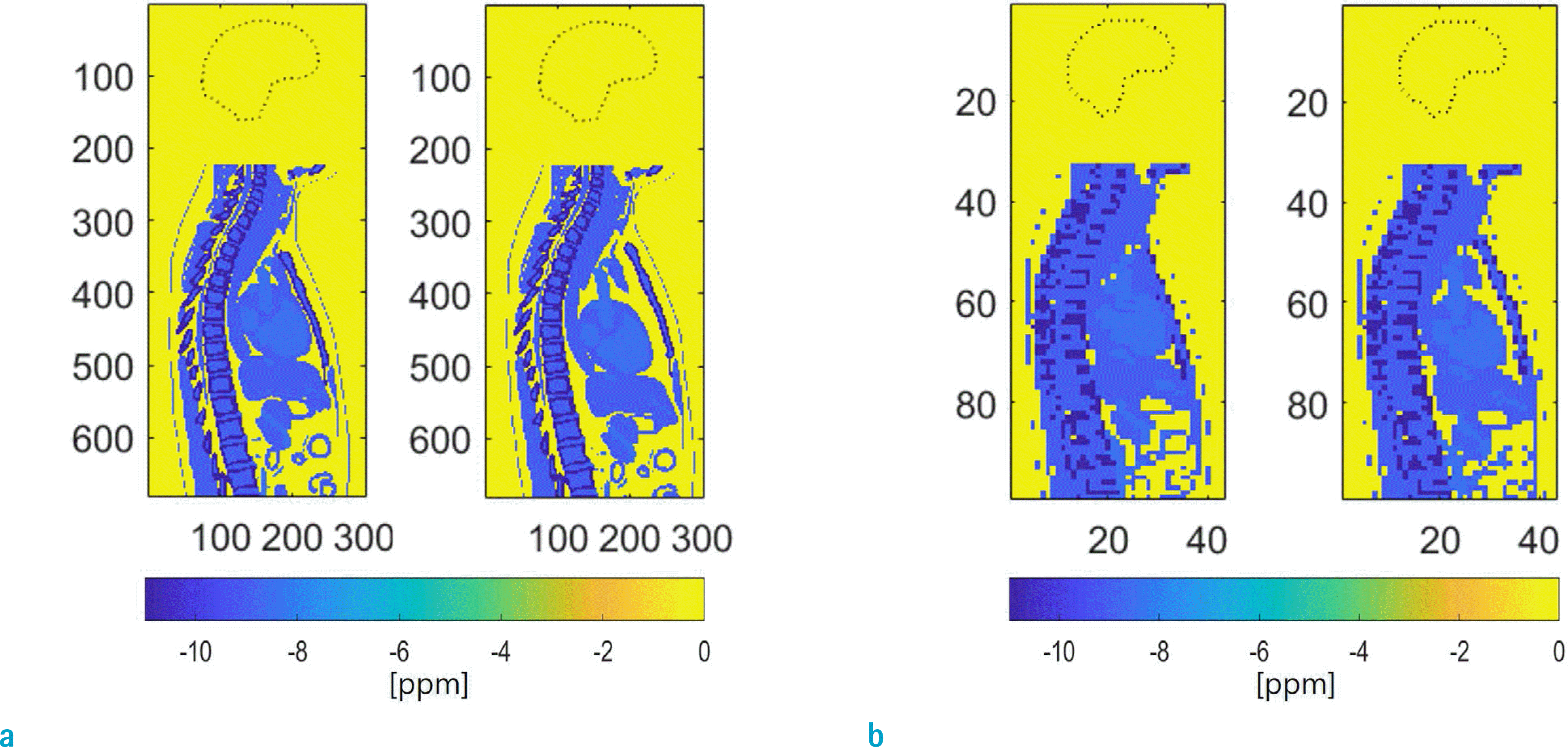
Fig. 2.

Midsagittal view of the respiration-induced B₀ shift in the brain at 7T at 10 time points in a breathing cycle. Time order is from left-to-right. The B₀ calculation algorithm gSVC was used. (a) and (b) correspond to voxel sizes of 0.1 cm and 0.7 cm, respectively. Note significant differences between B₀ shifts computed at 0.7 cm vs. 0.1 cm resolution.

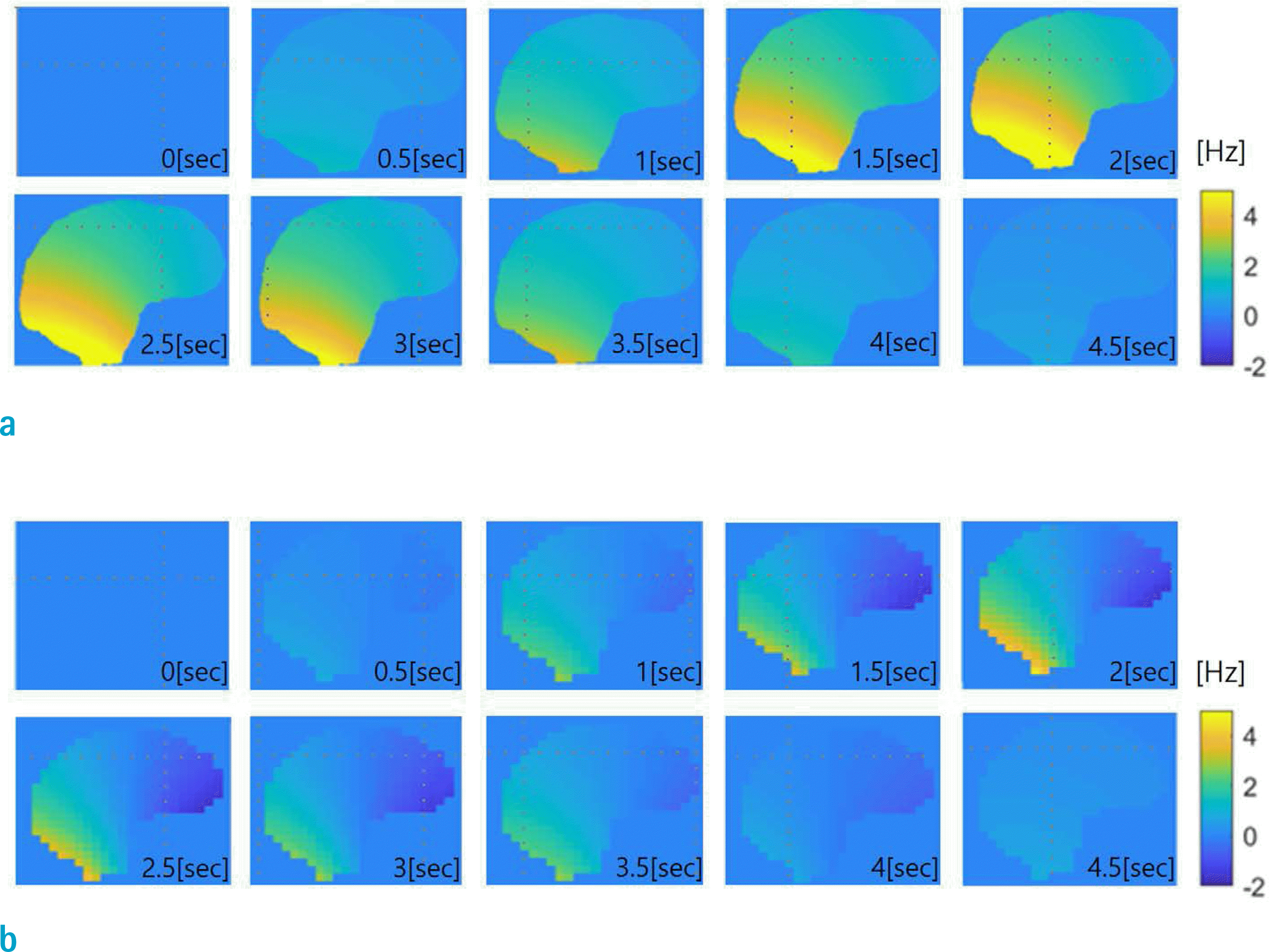
Fig. 3.

Time dependence of B₀ shift statistics in the brain during breathing computed at 0.1 cm voxel size. Maximum B₀ shift of 7.2 Hz is observed at 2 s (5^th frame).

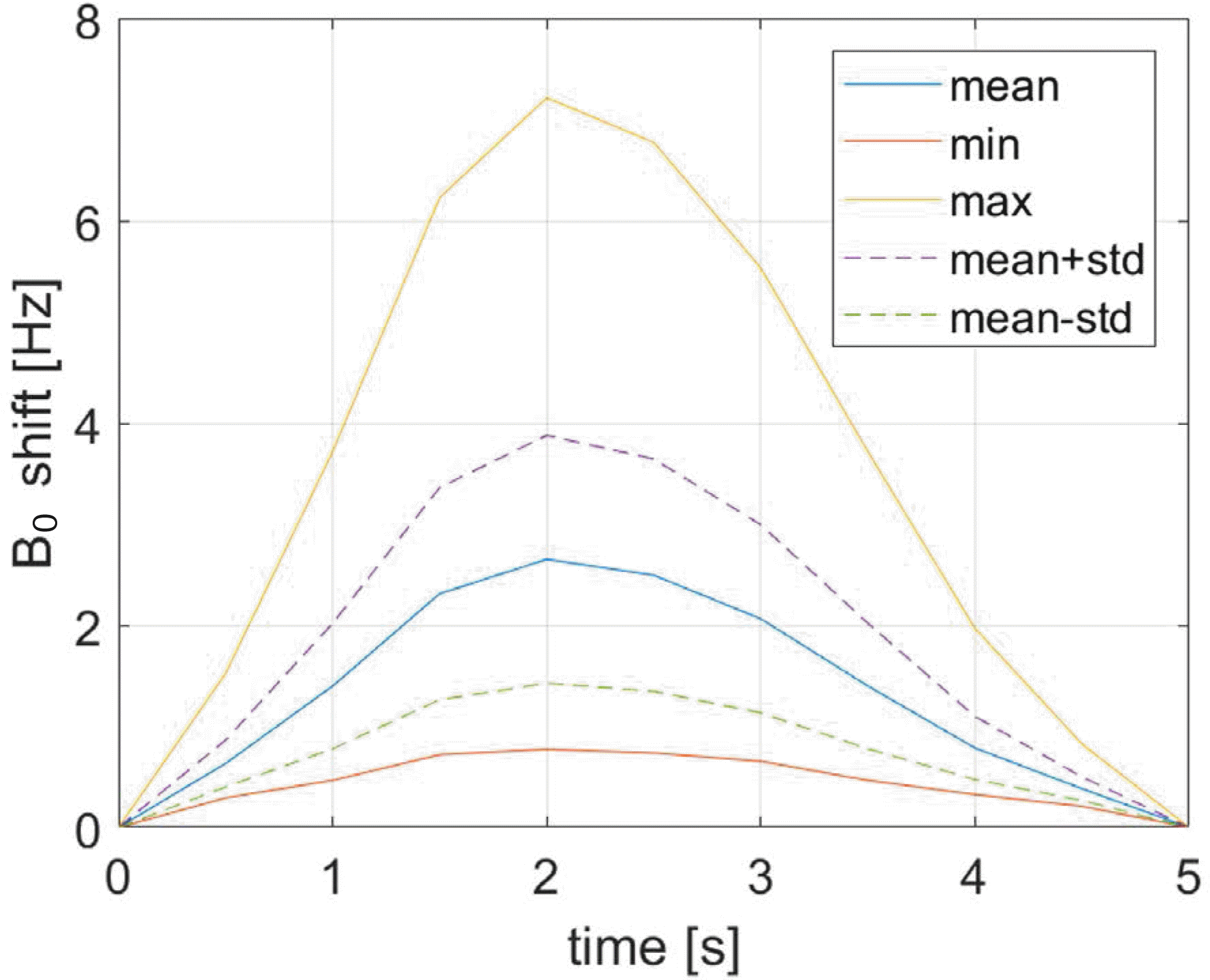
Fig. 4.

Mean B₀ shift gradients in the brain at the 5^th frame (fully-inhaled), computed at 0.1 cm voxel resolution, along the x (left-to-right, a), y (posterior-to-anterior, b), z (foot-to-head, c) directions. The blue traces correspond to B₀ values averaged over slices normal to each direction. The straight lines indicate linear fitting to the data.

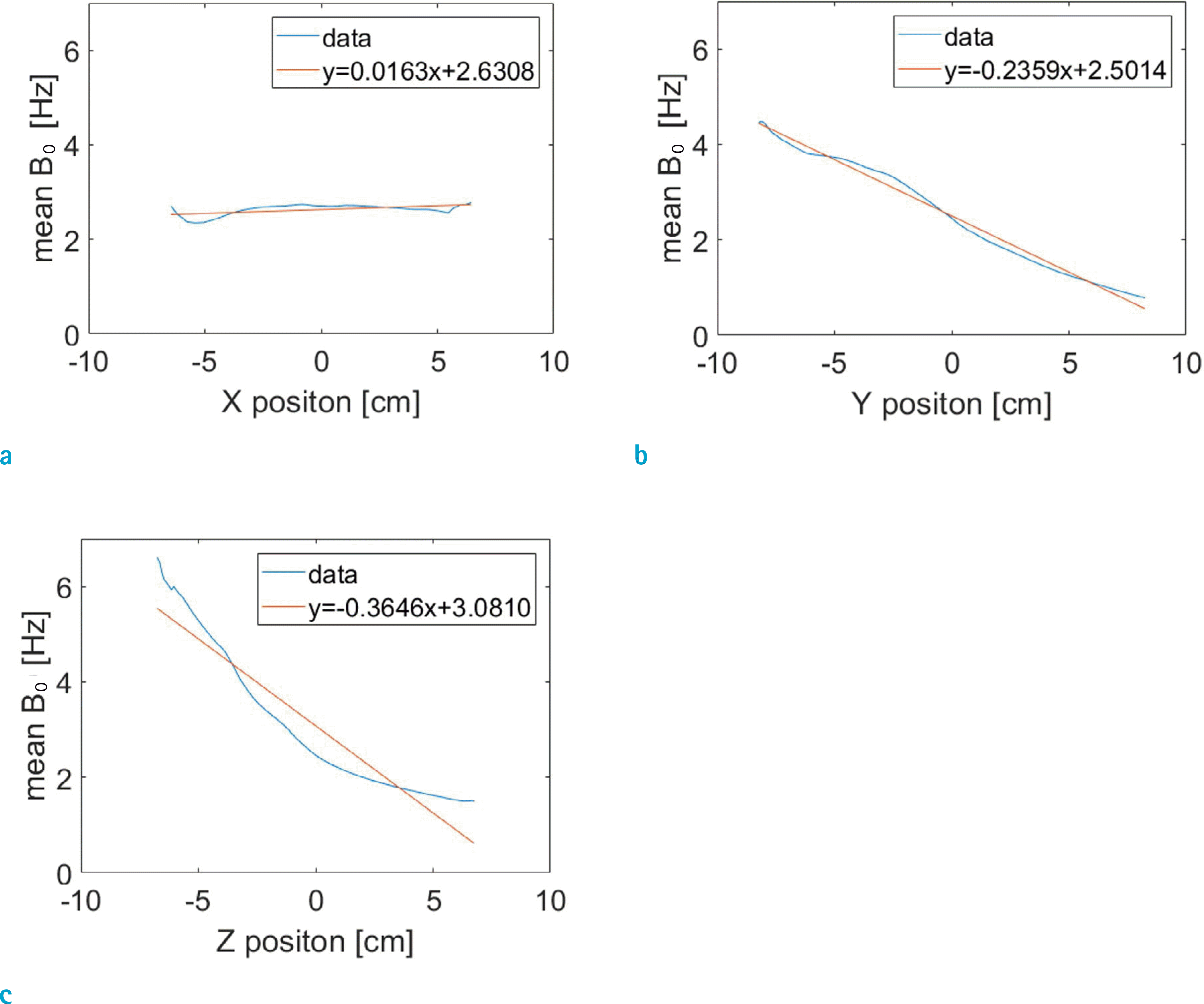
Fig. 5.

Plot of B₀ shift gradients as a function of time at 0.1 cm voxel resolution. The gradient values were obtained by volumetric linear fitting at each time point. The maximum gradient amplitudes in the y, z directions are observed at 2 s (5^th frame). Gradient in the x-direction shows little change.

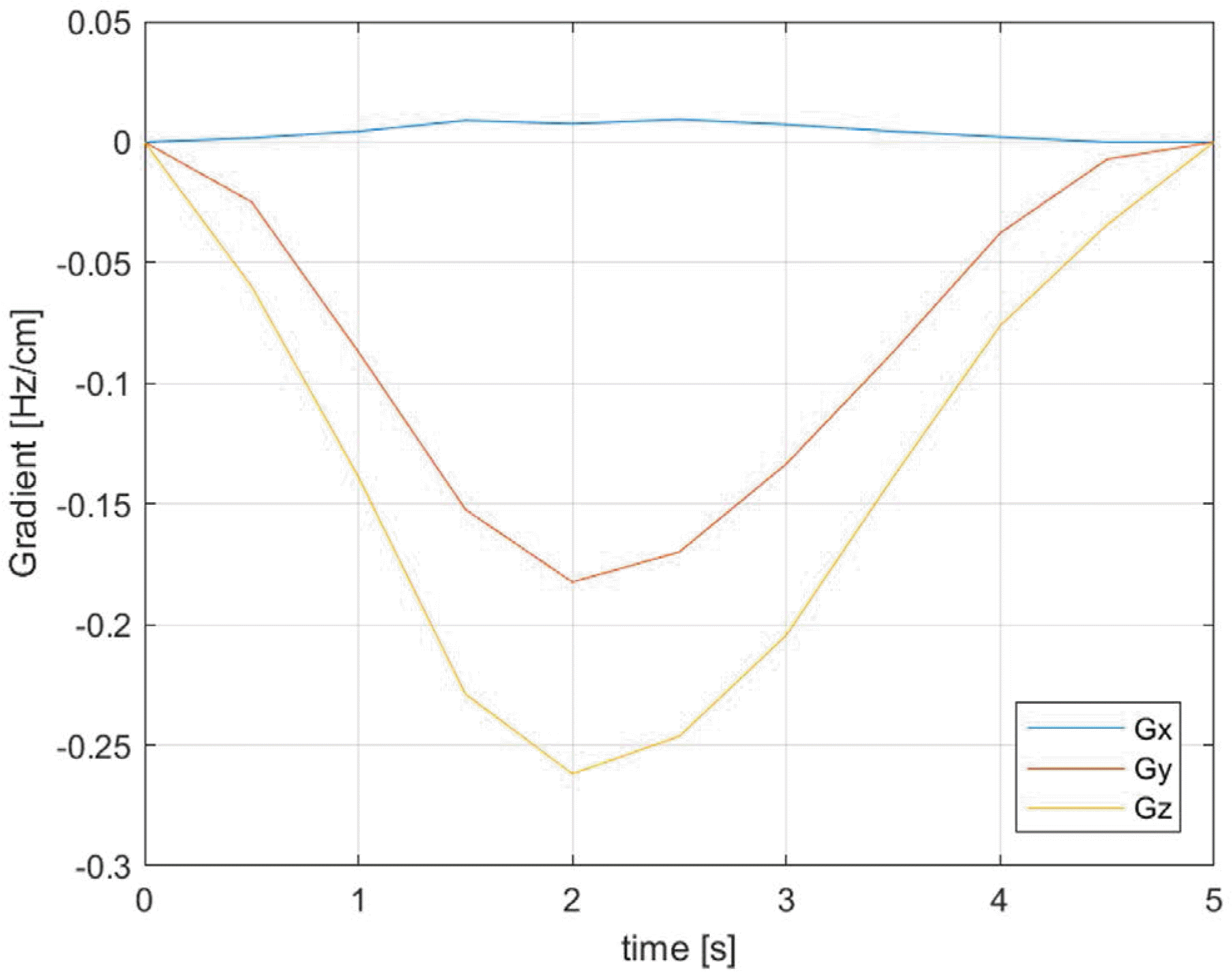
Fig. 6.

Plot of B₀ shift gradients at frame 5 relative to frame 1 as a function of the voxel size. The gradient values become increasingly more erratic as the voxel size increases, indicating reduced reliability at large voxel sizes (larger than about 0.5 cm).

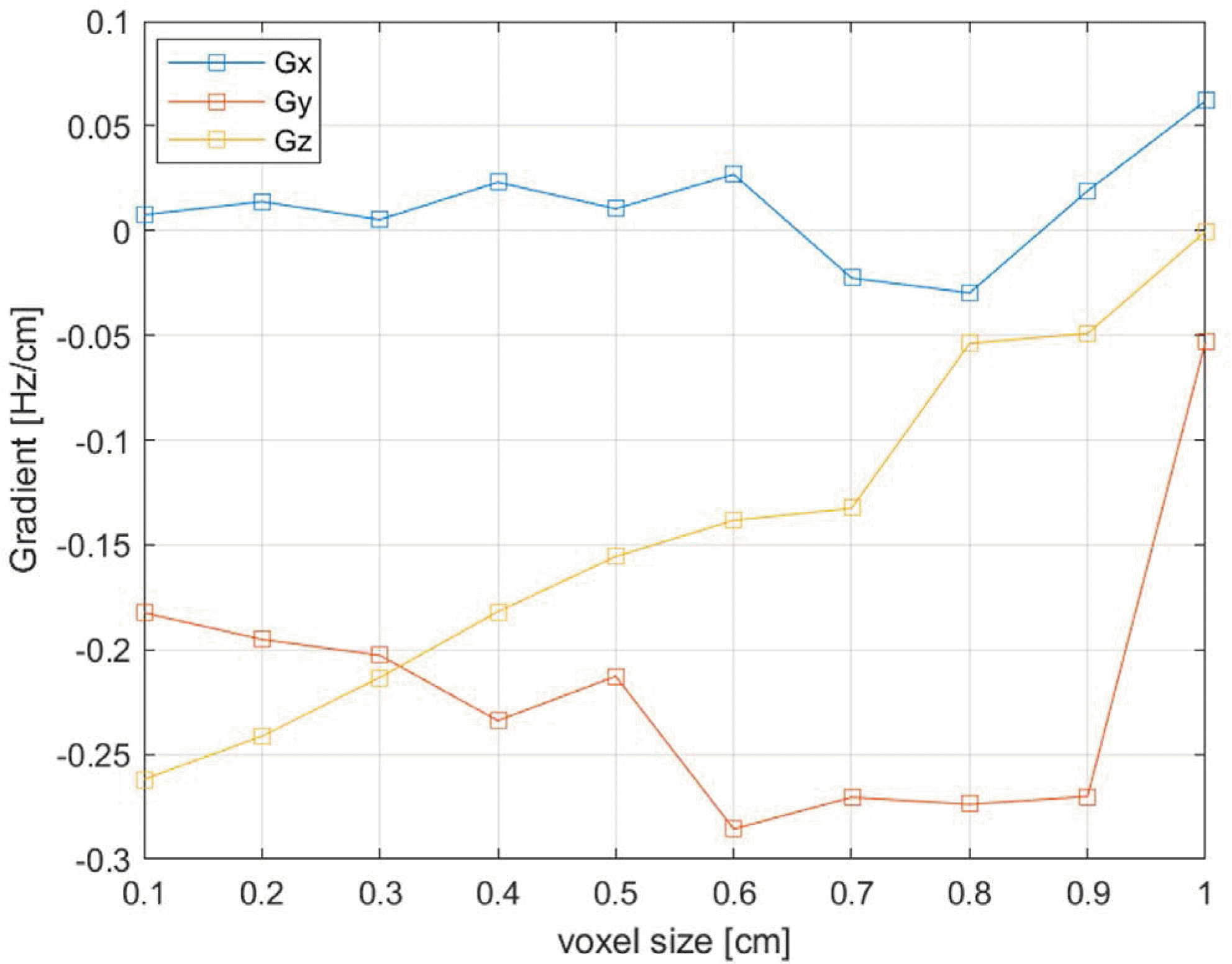
Table 1.

Susceptibility source (torso) and B₀ calculation target (head) positions, computational times, and respiration-induced B₀ gradients at different human body model resolutions. The computational times are divided between the dipolar field kernel calculation (t₁) and dynamic B₀ update (t₂)

Voxel size (cm)		0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
Torso slice indices	Start slice*	1100	550	367	275	220	183	157	138	122	110
	End slice	1560	780	520	390	312	260	223	195	173	156
Head slice indices	Start slice	1620	810	540	405	324	270	231	203	180	162
	End slice	1780	890	593	445	356	297	254	223	198	178
t₁ (s)		12.045	1.808	0.471	0.241	0.127	0.0725	0.0451	0.0269	0.0224	0.0181
t₂ (s)		77.398	11.874	2.529	1.346	0.604	0.4022	0.1872	0.1315	0.1086	0.0809
Gx (Hz/cm)**		0.0076	0.0139	0.0053	0.0231	0.0105	–0.0269	–0.0226	–0.0297	0.0190	0.0620
Gy (Hz/cm)		–0.1824	–0.1951	–0.2027	–0.2339	–0.2127	–0.2856	–0.2705	–0.2738	–0.2701	–0.0532
Gz (Hz/cm)		–0.2619	–0.2413	–0.2133	–0.1819	–0.1555	–0.1383	–0.1325	–0.0538	–0.0491	–0.0004

^* Slice index rises in the foot-to-head direction.

^** B₀ gradients were calculated by linear function fitting in the x (left to right), y (posterior to anterior), and z (foot to head) directions.

TOOLS

Similar articles