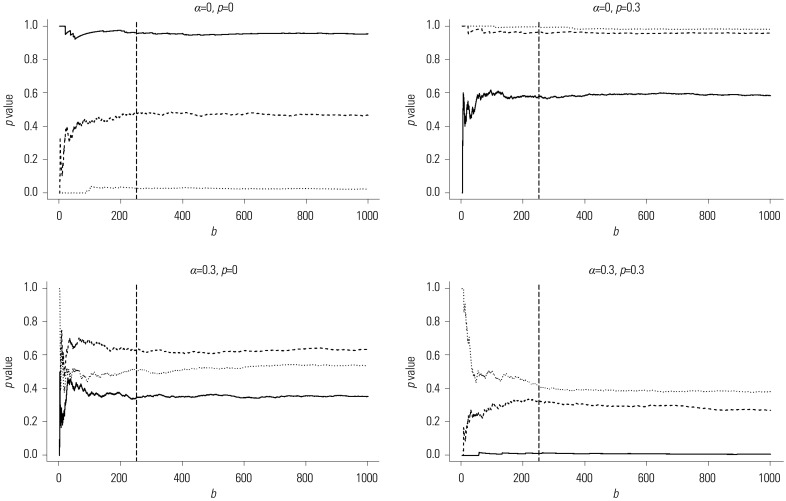
Based on the proposed test statistic
Q(ε
1,ε
2), we split the patients into two groups for relapse, a high-risk group and a low-risk group, to apply different treatments to each group. We set ε
1 and ε
2 as 0.1 and 0.9, respectively. As shown in
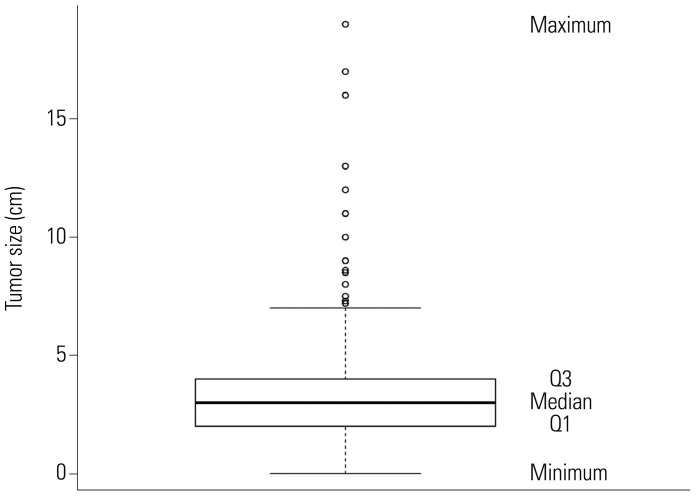
Table 3, at the first split of 758 patients, the criterion was tumor size of 1.8, and the CIFs for relapse of the two groups were different (
p value<0.001). We further investigated whether the patients within each subgroup were homogeneous in experiencing relapse after surgery in terms of
Q(ε
1,ε
2). The group with a tumor size less than or equal to 1.8 was statistically homogeneous (
p value=0.096), while the group having tumor size greater than 1.8 was not homogeneous (
p value<0.001). In the same way, we applied a binary split of only the group with a tumor size greater than 1.8. The next split criterion was a tumor size of 3, and only the group with a tumor size greater than 3 was not homogeneous (
p value=0.020). The third split was 6.5, and both groups, tumor size less than or equal to 6.5 or greater than 6.5, were homogeneous with
p values of 0.530 and 0.957, respectively. The top left panel of
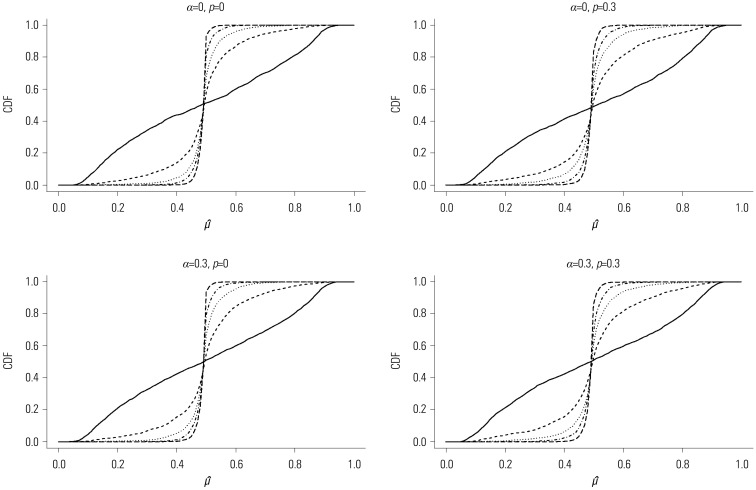
Fig. 4 depicts the standardized linear rank statistics
Tµ against tumor size (solid line). The 1st, 10th, 90th, and 99th quantile points of tumor size along with the estimated cutpoint μ̂ of 1.8 are indicated on the axis of tumor size with symbols of black square, black circle, black triangle, and black diamond, respectively. In the top right panel, the CIFs of two groups, tumor size greater than 1.8 (dashed line) and less than or equal to 1.8 (solid line), are displayed. In the same way, plots in the second and third rows of
Fig. 4 are respectively drawn with the subgroups of 594 patients having tumor size greater than 1.8 and of 334 patients having tumor size greater than 3. In summary, we could classify the patients with tumor size less than or equal to 1.8 into a low-risk group, while the patients included in a high-risk group (i.e., having tumor size more than 1.8) could be further classified into three subgroups, lowest, moderate, and highest high-risk groups, depending on tumor sizes at surgery of 1.8 to 3, 3 to 6.5, and over 6.5, respectively.
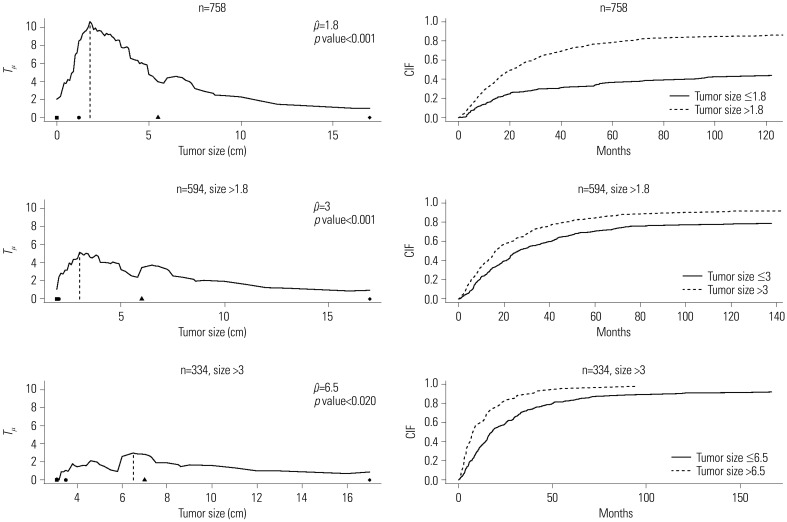 | Fig. 4Plot of standardized linear rank statistic and cumulative incidence function (CIFs) of two groups classified depending on the estimated cutpoint. Left panel: standardized linear rank statistic Tµ against tumor size (solid line), estimated cutpoint (dashed line), and the 1st, 10th, 90th, and 99th quantile points of tumor size of each sub-sample (black square, black circle, black triangle, and black diamond in order). Right panel: CIF for the event time of interest of two groups, ≤ and > μ̂.
|
Table 3
Split Criterion of the Covariate Size, the Number of Patients of Each Node, the Estimated Cutpoint μ̂, the Proposed Test Statistic Q(ε1,ε2), and Approximated and Permutation-Based p values
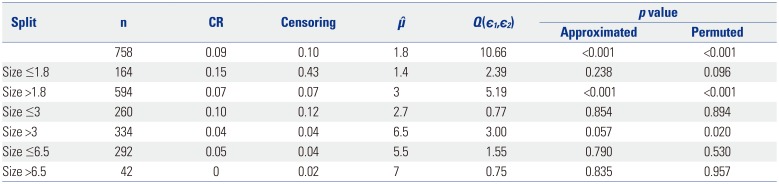
|
Split |
n |
CR |
Censoring |
μ̂ |
Q(є1,є2) |
p value |
|
Approximated |
Permuted |
|
758 |
0.09 |
0.10 |
1.8 |
10.66 |
<0.001 |
<0.001 |
|
Size ≤1.8 |
164 |
0.15 |
0.43 |
1.4 |
2.39 |
0.238 |
0.096 |
|
Size >;1.8 |
594 |
0.07 |
0.07 |
3 |
5.19 |
<0.001 |
<0.001 |
|
Size ≤3 |
260 |
0.10 |
0.12 |
2.7 |
0.77 |
0.854 |
0.894 |
|
Size >;3 |
334 |
0.04 |
0.04 |
6.5 |
3.00 |
0.057 |
0.020 |
|
Size ≤6.5 |
292 |
0.05 |
0.04 |
5.5 |
1.55 |
0.790 |
0.530 |
|
Size >;6.5 |
42 |
0 |
0.02 |
7 |
0.75 |
0.835 |
0.957 |


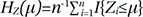 denote the empirical distribution function of the prognostic factor Z. Let mµ=nHZ(µ) and nµ=n−mµ. Following the arguments,125 under H0, given the scores, the expectation and the variance of Lµ are
denote the empirical distribution function of the prognostic factor Z. Let mµ=nHZ(µ) and nµ=n−mµ. Following the arguments,125 under H0, given the scores, the expectation and the variance of Lµ are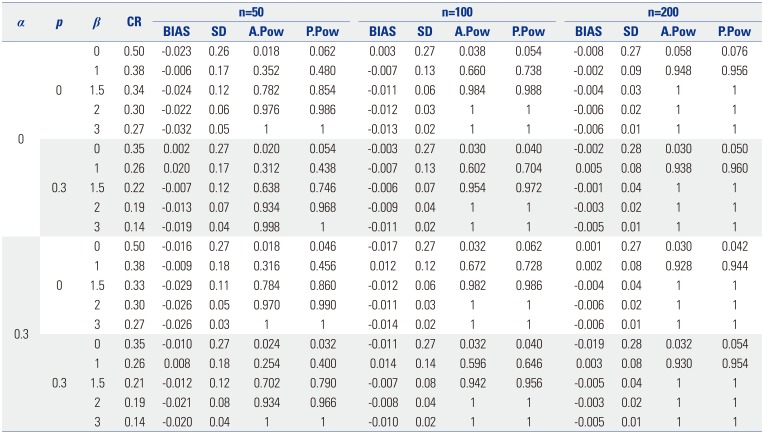


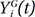 excludes the contribution of the subjects who are censored by an earlier occurrence of the competing risks than an event of interest, as suggested by a referee, we could replace this process by the following process,15
excludes the contribution of the subjects who are censored by an earlier occurrence of the competing risks than an event of interest, as suggested by a referee, we could replace this process by the following process,15




 PDF
PDF ePub
ePub Citation
Citation Print
Print



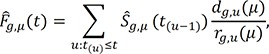
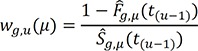
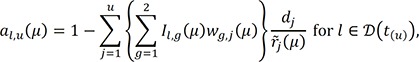
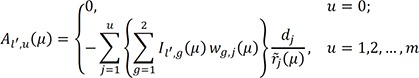
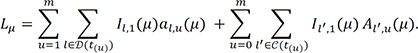
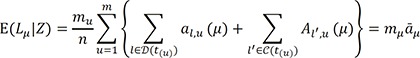
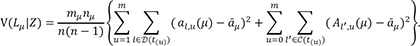
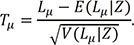
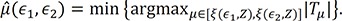
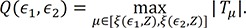
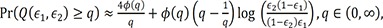
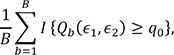
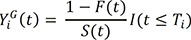
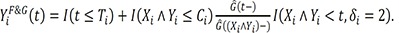
 XML Download
XML Download