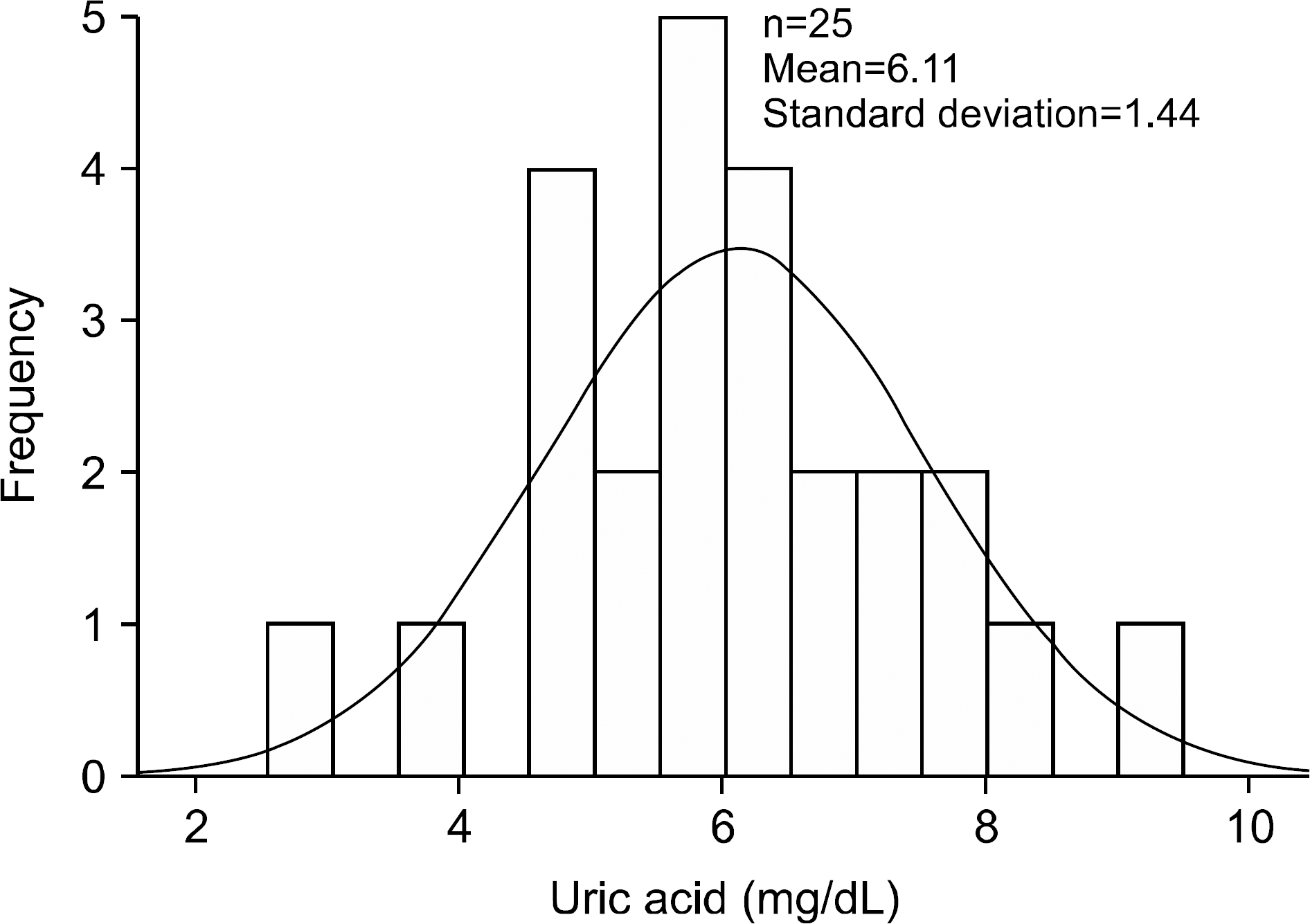
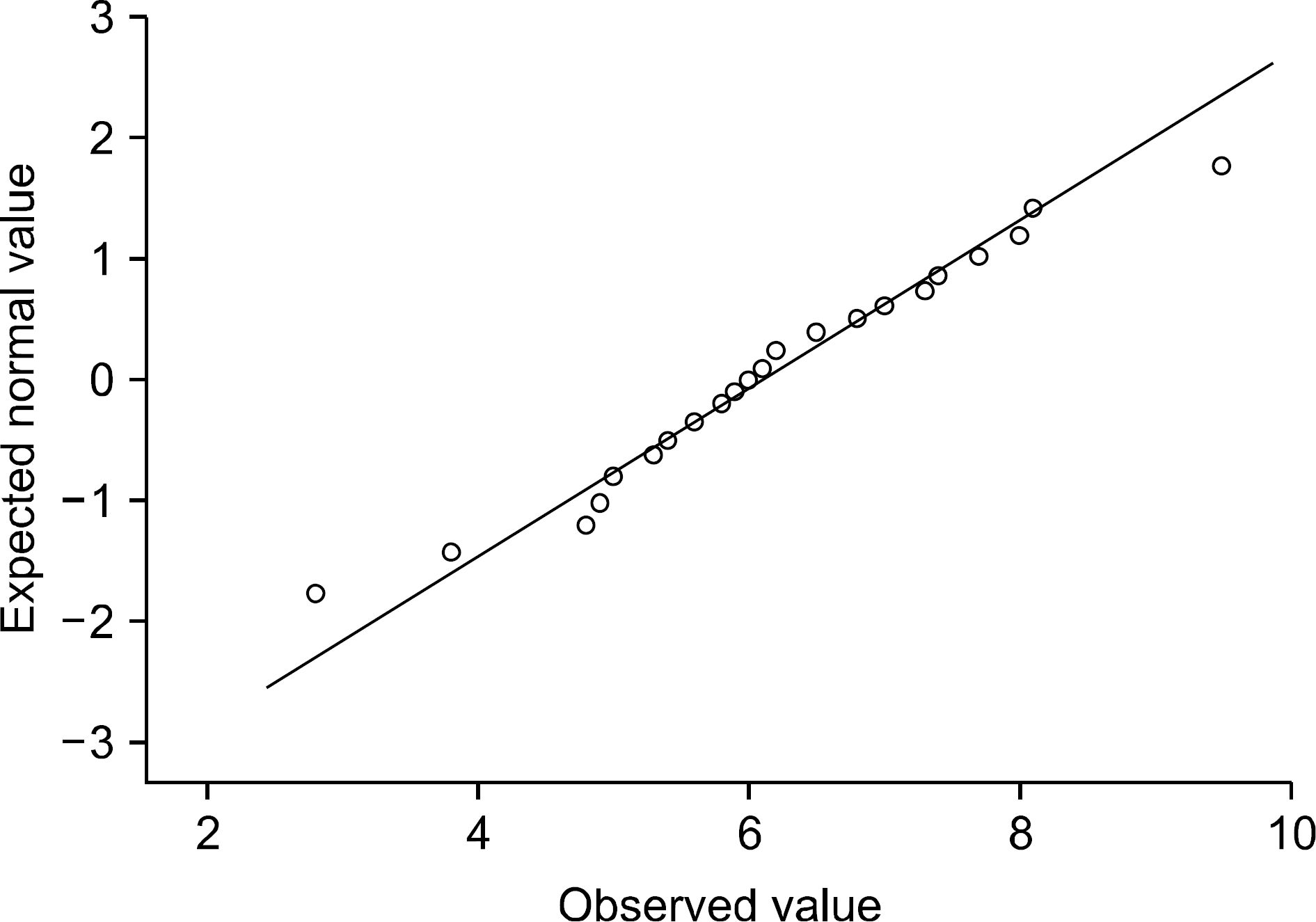
In data analysis, given that various statistical methods assume that the distribution of the population data is normal distribution, it is essential to check and test whether or not the data satisfy the normality requirement. Although the analytical methods vary depending on whether or not the normality is satisfied, inconsistent results might be obtained depending on the analysis method used. In many clinical research papers, the results are presented and interpreted without checking or testing normality. According to the central limit theorem, the distribution of the sample mean satisfies the normal distribution when the number of samples is above 30. However, in many clinical studies, due to cost and time restrictions during data collection, the number of samples is frequently lower than 30. In this case, a proper statistical analysis method is required to determine whether or not the normality is satisfied by performing a normality test. In this regard, this paper discusses the normality check, several methods of normality test, and several statistical analysis methods with or without normality checks.