WHAT IS THE DIFFERENCE BETWEEN MACHINE LEARNING AND A COMPUTER PROGRAM?
A computer program takes input data, processes the data, and outputs a result. A programmer stipulates how the input data should be processed. In machine learning, input and output data is provided, and the machine determines the process by which the given input produces the given output data.
123 This process can then predict the unknown output when new input data is provided.
123
So, how does machine determine the process? Consider a linear model,
y =
Wx +
b. If we are given the
x and
y values shown in
Table 1, we know intuitively that
W = 2 and
b = 0.
Table 1
Example dataset for the linear model y = Wx + b

|
x
|
y
|
|
1 |
2 |
|
2 |
4 |
|
3 |
6 |
|
4 |
8 |
|
5 |
10 |
|
10 |
20 |
|
20 |
40 |
|
30 |
60 |

However, how does a computer know what
W and
b are?
W and
b are randomly generated initially. For example, if we initially say
W = 1 and
b = 0 and input the
x values from
Table 1, the predicted
y values do not match the
y values in the
Table 1. At this point, there is a difference between the correct
y values and the predicted
y values; the machine gradually adjusts the values of
W and
b to reduce this difference. The difference between the predicted values and the correct values is called the cost function. Minimizing the cost function makes predictions closer to the correct answers.
4567
 | Fig. 1
|
ARTIFICIAL NEURAL NETWORK
The basic unit by which the brain works is a neuron. Neurons transmit electrical signals (action potentials) from one end to the other.
11 That is, electrical signals are transmitted from the dendrites to the axon terminals through the axon body. In this way, the electrical signals continue to be transmitted across the synapse from one neuron to another. The human brain has approximately 100 billion neurons.
1112 It is difficult to imitate this level of complexity with existing computers. However, Drosophila have approximately 100,000 neurons, and they are able to find food, avoid danger, survive, and reproduce.
13 Nematodes have 302 neurons and they survive well.
14 This is a level of complexity that can be replicated well even with today's computers. However, nematodes can perform much better than our computers.
Let's think of the operative principles of neurons. Neurons receive signals and generate other signals. That is, they receive input data, perform some processing, and give an output.
1112 However, the output is not given at a constant rate; the output is generated when the input exceeds a certain threshold.
15 The function that receives an input signal and produces an output signal after a certain threshold value is called an activation function.
1115 As shown in
Fig. 2, when the input value is small, the output value is 0, and once the input value rises above the threshold value, a non-zero output value suddenly appears. Thus, the responses of biological neurons and artificial neurons (nodes) are similar. However, in reality, artificial neural networks use various functions other than activation functions, and most of them use sigmoid functions.
46 which are also called logistic functions. The sigmoid function has the advantage that it is very simple to calculate compared to other functions. Currently, artificial neural networks predominantly use a weight modification method in the learning process.
457 In the course of modifying the weights, the entire layer requires an activation function that can be differentiated. This is because the step function cannot be used as it is. The sigmoid function is expressed as the following equation.
616
 | Fig. 2 A step function and a sigmoid function.
|
Biological neurons receive multiple inputs from pre-synaptic neurons.
11 Neurons in artificial neural networks (nodes) also receive multiple inputs, then they add them and process the sum with a sigmoid function.
57 The value processed by the sigmoid function then becomes the output value. As shown in
Fig. 3, if the sum of inputs A, B, and C exceeds the threshold and the sigmoid function works, this neuron generates an output value.
4
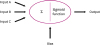 | Fig. 3 Input and output of information from neurons.
|
A neuron receives input from multiple neurons and transmits signals to multiple neurons.
45 The models of biological neurons and an artificial neural network are shown in
Fig. 4. Neurons are located over several layers, and one neuron is considered to be connected to multiple neurons. In an artificial neural network, the first layer (input layer) has input neurons that transfer data via synapses to the second layer (hidden layer), and similarly, the hidden layer transfers this data to the third layer (output layer) via more synapses.
457 The hidden layer (node) is called the “black box” because we are unable to interpret how an artificial neural network derived a particular result.
456
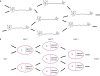 | Fig. 4 (A) Biological neural network and (B) multi-layer perception in an artificial neural network.
|
So, how does a neural network learn in this structure? There are some variables that must be updated in order to increase the accuracy of the output values during the learning process.
457 At this time, there could be a method of adjusting the sum of the input values or modifying the sigmoid function, but it is a rather practical method to adjust the connection strength between the neurons (nodes).
457 Fig. 5 is a reformulation of
Fig. 4 with the weight to be applied to the connection strength. Low weights weaken the signal, and high weights enhance the signal.
17 The learning part is the process by which the network adjusts the weights to improve the output.
457 The weights
W1,2,
W1,3,
W2,3,
W2,2, and
W3,2 are emphasized by strengthening the signal due to the high weight. If the weight
W is 0, the signal is not transmitted, and the network cannot be influenced.
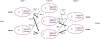 | Fig. 5 The connections and weights between neurons of each layer in an artificial neural network.
|
Multiple nodes and connections could affect predicted values and their errors. In this case, how do we update the weights to get the correct output, and how does learning work?
The updating of the weights is determined by the error between the predicted output and the correct output.
457 The error is divided by the ratio of the weights on the links, and the divided errors are back propagated and reassembled (
Fig. 6). However, in a hierarchical structure, it is extremely difficult to calculate all the weights mathematically. As an alternative, we can use the gradient descent method
8910 to reach the correct answer — even if we do not know the complex mathematical calculations (
Fig. 1). The gradient descent method is a technique to find the lowest point at which the cost is minimized in a cost function (the difference between the predicted value and the answer obtained by the arbitrarily start weight
W). Again, the machine can start with any
W value and alter it gradually (so that it goes down the graph) so that the cost is reduced and finally reaches a minimum. Without complicated mathematical calculations, this minimizes the error between the predicted value and the answer (or it shows that the arbitrary start weight is correct). This is the learning process of artificial neural networks.
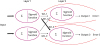 | Fig. 6 Back propagation of error for updating the weights.
|






 PDF
PDF ePub
ePub Citation
Citation Print
Print









 XML Download
XML Download