How to evaluate the adequacy of staging for nodal-negative epithelial ovarian cancer? Use of nodal staging score

Yuan Xu; Haoran Li; Xiaoxia Tong; Yangyang Pang; Xiaojuan Tong; Luhong Li; Lei Cheng

doi:10.3802/jgo.2019.30.e21

Journal List > J Gynecol Oncol > v.30(2) > 1116726

Go to TopGo to Top Go to BottomGo to Bottom

TOOLS

Xu, Li, Tong, Pang, Tong, Li, and Cheng: How to evaluate the adequacy of staging for nodal-negative epithelial ovarian cancer? Use of nodal staging score

Original Article

Ovary

Journal of Gynecologic Oncology 2019; 30(2): e21.

Published online: 4 December 2018

DOI: https://doi.org/10.3802/jgo.2019.30.e21

How to evaluate the adequacy of staging for nodal-negative epithelial ovarian cancer? Use of nodal staging score

Yuan Xu^1,^*

, Haoran Li^2,^3,^*

, Xiaoxia Tong³

, Yangyang Pang⁴

, Xiaojuan Tong⁵

, Luhong Li⁶

, Lei Cheng^3,⁷

¹Department of Pulmonary and Critical Care Medicine, Second Affiliated Hospital of Fujian Medical University, Respiratory Medicine Center of Fujian Province, Quanzhou, China.

²Department of Gynecological Oncology, Fudan University Shanghai Cancer Center, Shanghai, China.

³Department of Oncology, Shanghai Medical College, Fudan University, Shanghai, China.

⁴Department of Surgery, Jiading Central Hospital, Shanghai, China.

⁵Department of General Family Medicine, The First Affiliated Hospital of Zhejiang Chinese Medical University, Hangzhou, China.

⁶Department of Gynecology and Obstetrics, The Second Affiliated Hospital of Fujian Medical University, Quanzhou, China.

⁷Department of Medical Oncology, Fudan University Shanghai Cancer Center, Shanghai, China.

Correspondence to Lei Cheng. Department of Medical Oncology, Fudan University Shanghai Cancer Center, 270 Dong'an Road, Shanghai, China and Department of Oncology, Shanghai Medical College, Fudan University, 138 Yixueyuan Road, Shanghai, China. leiel_cheng@163.com

Equal contributor:

*Yuan Xu and Haoran Li contributed equally to this work.

Received 28 June 2018 Revised 24 July 2018 Accepted 31 October 2018

Asian Society of Gynecologic Oncology, Korean Society of Gynecologic Oncology

(open-access):

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

Objective

No guideline has been provided to assess the minimal number of lymph nodes (LNs) that should be dissected for accurate staging in patients with epithelial ovarian cancer (EOC). The aim of the study was to develop a nodal staging score (NSS) as an index to assess whether a pathologic (p)N0 EOC patient is indeed free of a nodal disease.

Methods

A total of 16,361 EOC patients staged I–III between 2004 and 2013 were identified from the Surveillance, Epidemiology and End Result database. With a β-binomial model, NSS was calculated to assess the probability of true-negative findings of LN status.

Results

With an increased number of LNs examined, the probability of missing a nodal disease decreased and varied among different pT stages. Given 1 LN examined, an NSS of 93.76% calculated could ensure a high adequacy of nodal-negative classification for pT1N0 EOC patients. For pT2N0 patients, 5 LNs examined could guarantee an NSS of 90% for adequate staging. Likewise, 11 and 29 LNs examined in pT3N0 patients could maintain NSS at the level of 80% and 90%, respectively. Our study suggested the optimal number of LNs that could be examined and stratified by the pT stages for EOC patients based on this statistical model derived from large pathologic data of clinical surgery patients.

Conclusion

NSS, as an auxiliary tool, not only could assist the International Federation of Gynecology and Obstetrics staging more precisely, but also would provide a statistical basis for postoperative evaluation for further clinical decision-making.

Keywords: Epithelial Ovarian Cancer, Lymph Node Dissection, Cancer Staging, Prognosis

INTRODUCTION

Epithelial ovarian cancer (EOC) is one of the most lethal malignancies with a relatively high incidence in developed countries [1]. With the exploratory analysis based on prospective trial and large epidemiologic series in early-stage EOC, prognostic value of comprehensive lymphadenectomy (LNE) has also been confirmed [2 3]. Under the current National Comprehensive Cancer Network guideline [4], dissection of systemic pelvic and para-aortic lymph nodes (LNs) is recommended for an early-stage EOC, and resection of suspicious and enlarged LNs is recommended for advanced-stage disease. However, the exact number of LNs to be resected is not mentioned.

The American Joint Committee on Cancer (AJCC) staging system, in terms of postoperative pathological examination of LNs, defines that patients with all peritoneal status but positive LNs are staged as T3c, which is also called stage IIIC by the International Federation of Gynecology and Obstetrics (FIGO) guidelines. Pelvic and para-aortic LNE is one part of comprehensive surgical staging to explore the accurate status of LN metastasis; approximately 30% of patients with apparent early-stage undergo being upstaged after comprehensive lymphatic and peritoneal staging [5]. Although EOC patients could benefit from the standard staging system, it is highly possible to be under-staged, if a limit number of LNs are dissected and pathologically examined. Thus, a nodal staging score (NSS), which is the probability that a patient is properly diagnosed as nodal-negative, has been proposed [5 6 7]. And 1-NSS is the probability that a nodal-positive patient is under-staged as nodal-negative. With this statistical model, we can estimate the probability that a pathologically nodal-negative patient is indeed free of nodal disease. Up to now, NSS has been established successfully for several malignancies, including cancers of colon [6], prostate [7], and bladder [8]. However, the role of NSS in EOC has still not been fully illustrated. In the present study, we established NSS as a function of the number LNs examined and patients' pathologic T stage among EOC patients from a population-based database, the Surveillance, Epidemiology and End Results (SEER).

MATERIALS AND METHODS

1. Data source

The SEER database, a population-based registry, is sponsored by the National Cancer Institute (NCI). With 18 population-based cancer registries, the SEER program covers approximately 28% of the cancer registries from the United States [9 10]. In view of the data from SEER database were de-identified, written informed consent cannot be assessed.

The NCI's SEER^*Stat Software (version 8.1.2; IMS Inc., Calverton, MD, USA; https://seer.cancer.gov/seerstat) was used to identify EOC patients diagnosed between 2004 and 2013. We included patients histologically confirmed EOC based on the International Classification of Diseases for Oncology, 3rd edition. From the SEER database, the detailed clinicopathologic information, including the AJCC staging (AJCC 7th), number of examined LNs, number of pathologically positive LNs and survival data were extracted for the analysis. Patients were restaged based on the AJCC 7th staging system, if only the information on the AJCC 6th staging was available.

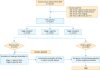
2. Statistical methods

To precisely estimate the probability of false-negative findings of the LN status due to missing a nodal disease, the data were simulated to reach the real situation to the greatest extent. Then, a β-binomial distribution was fitted to the simulated data to calculate this false-negative probability [7]. Using the results derived from this modeling, NSS was finally calculated with 2 further steps:

1) Step 1: simulate the data of missing a detectable LN based on nodal-positive patients

To reach the real status of LNs metastasis more precisely, we performed the data simulation of missing a detectable LN.

A nodal positive patient indicated by the SEER database is a patient who has at least 1 pathologically metastatic lymph nodal. To precisely assess the probability of false negative findings—all of LNs examined were negative for a factually nodal positive patient, we established a dataset of false-negative patients containing 20% of pT1-2 patients and 40% of pT3 patients, respectively. Using a part of nodal-positive patients randomly selected from the dataset, we performed a data simulation as missing a LN that was randomly assigned for each patient. We assumed that n was the number of total LNs examined and i was the number of positive LNs examined for each patient; given n LNs examined, the patient was simulated as having 1 LN missed and therefore only n-1 LNs were examined. In the process of simulation, positive LNs for each patient were numbered from 1 to i and the negative LNs were numbered i+1 to n. Then, we generated a random positive integer termed rx from 1 to n, which was distributed uniformly. If rx≤i, the corresponding patient was simulated to have missed a detectable positive LN; otherwise in the condition of rx>i, the corresponding patient was simulated to have missed a detectable negative LN. Through the process of simulation, the dataset was assumed to contain false-negative patients. Then we construct a β-binomial model to assess the probability of false-negative findings due to missing a nodal disease based on the simulated dataset.

2) Step 2: compute the probability of failing to detect a nodal disease using a β-binomial distribution

In the following β-binomial model, we assumed that n was the number of total LNs examined from a patient, and i (i≥0) was the number of positive LNs examined based on the simulation data set. The β-binomial was listed below, where B (.) was a β function. The maximum likelihood method was used to estimate the parameters α and β.

(1)

(\begin{matrix} n \\ i \end{matrix}) \frac{B (i + α, n + β - i)}{B (α + β)}

In this model, k=n-i, represented the number of negative LNs for a patient. Data on jth patient was expressed as n_j, i_j, and k_j, respectively (1≤k_j<n_j, j=1, 2,……N).

(2)

P ({F N}_{k}) = P (i_{j} = 0| k, α, β) = \frac{B (α, k + β)}{B (α, β)}

P (FN_k) was the probability of all LNs examined negative (n=k, i=0) for an actually a LN-positive patient due to missing a nodal disease. To compute the probability of failing to detect a nodal disease, we assumed n=k in the above model. To ensure the accuracy for the fitted results, two assumptions should be fulfilled before the use of the statistical model s: firstly, it was the false-negative assumption that the positive LN was missed due to limited LNs examined intraoperatively; secondly, there was no false-positive results for LN pathological examination postoperatively.

3) Step 3: calculate the prevalence of nodal disease adjusted by false-negative probability

With the false-negative probability calculated from the above-mentioned steps, we estimated the adjusted prevalence of nodal disease stratified by pT stage:

(3)

# {F N}_{k} \approx \frac{P ({F N}_{k}) * {# T P}_{k}}{[1 - P ({F N}_{k})]}

For a given k- the total number of LNs excision, #TP_k and #FN_k represented the number of true nodal-positive and false nodal-negative patients.

(4)

P r e v (T_{j}) = \frac{Σ_{k} {(# F N}_{k} + # {T P}_{k})}{Σ_{k} {(# F N}_{k} + {# T P}_{k} {+ # T N}_{k})}

Prev (T_j) represents the adjusted prevalence of nodal disease stratified by the pT stage. TN_k is the number of true-negative patients.

4) Step 4: calculate the NSSs

(5)

{N S S}_{k | T j} = \frac{1 - P r e v (T_{j})}{1 - P r e v (T_{j}) + [P r e v (T_{j}) * P ({F N}_{k})]}

Finally, NSS_k|Tj(T=1, 2, 3) was calculated by the above-listed formula. It has 2 meanings of population- and individualized-based: the proportion of true nodal-negative EOC patients in pN0 patients with different pT stage, and the adequacy of a nodal-negative classification for those patients, respectively.

All statistical analysis was performed by using SAS (version 9.4; SAS Institute, Cary, NC, USA) and R (version 3.2.3; R Foundation, Vienna, Austria) software.

RESULTS

A flow-chart of the study design is shown in Fig. 1. From the SEER database, a total of 16,361 patents with stage I–III EOC were included in the analysis. The baseline characteristics of patients are listed in Table 1.

Fig. 1

The flowchart of this study.

AJCC, American Joint Committee on Cancer; EOC, epithelial ovarian cancer; ICD-O-3, International Classification of Diseases for Oncology, 3rd edition; LN, lymph node; LNE, lymphadenectomy; NSS, nodal staging score; SEER, the Surveillance, Epidemiology and End Results.

Table 1

Characteristics of patients included in this study

Characteristics		Node-negative (n=12,388)	Node-positive (n=3,973)	p-value^*
Age (yr)		56.74±12.78	59.41±12.61	<0.001
Race				<0.001
	White	10,434 (84.23)	3,413 (85.90)
	Black	572 (4.62)	221 (5.56)
	Others	1,382 (11.16)	339 (8.53)
T stage				<0.001
	T1	7,159 (43.76)	399 (2.44)
	T2	2,419 (14.79)	550 (3.36)
	T3	2,810 (17.17)	3,024 (18.48)
Total LN examined^†		11 (5–20)	11 (4–21)	0.081
Survival months^†		43 (19–74)	29 (13–51)	<0.001

Values are presented as mean±standard deviation, number (%), or median (range).

LN, lymph node.

^*Two-sided χ² test or Fisher's exact test for distributions between node-negative and node-positive patients; ^†Represented by median (25%–75% quartiles).

Stratified by the pT stage, the parameters α and β fitted in the β-binomial model are listed in Table 2. The probability of false-negative findings due to missing a nodal disease decreased with an increased number of LNs to be examined across all the pT stages (Fig. 2A) but varied in different pT stages, even the same number of LNs to have been examined.

Table 2

Parameters in fitness of β-binomial model

T stage	Percent of simulation (%)^*	α (95% CI)	β (95% CI)
T1	20	1.02 (0.84–1.19)	3.22 (2.56–4.06)
T2	20	0.90 (0.78–1.04)	1.78 (1.49–2.13)
T3	40	0.88 (0.83–0.93)	1.10 (1.02–1.19)

CI, confidence interval; LN, lymph node.

^*Percentage of patients in data simulation of missing a LN detected.

Fig. 2

Probability of false-negative LNE in EOC patients under β-binomial model (A). The NSS of nodal-negative diagnosis stratified by the pT stage (B).

LNE, lymphadenectomy; NSS, nodal staging score.

Compared with the apparent prevalence, the prevalence of nodal disease in EOC patients became higher across all the pT stages after the adjustment for the false-negative findings (Table 3), demonstrating that for pT1-3 stages patients, the understaged proportions were 2.78%, 6.63%, and 15.7%, respectively.

Table 3

Apparent and adjusted prevalence of nodal disease in EOC with different pathologic T stage

Pathologic T stage	Apparent prevalence	Adjusted prevalence^*
T1	5.28	8.06
T2	18.52	25.15
T3	51.83	67.53

Values are presented as percentage.

EOC, epithelial ovarian cancer.

^*Adjusted for the probability of missing a nodal disease.

As indicated by NSS (Fig. 2B), given 1 LN examined, we could declare that a pT1N0 patient was indeed node-negative with a 93.76% certainty. However, NSS decreased to 81.75% when 1 LN was examined for pT2 patients; but could reach to 90% accuracy of the staging, if 5 LNs were examined. For pT3 patients, NSS was merely 46.39% when 1 LN was examined; but 11 and 29 LNs to have been examined could maintain NSS at the levels of 80% and 90%, respectively.

The survival curve was presented as grouped by quartiles in each pT stage (Fig. 3). As expected, a high NSS could be regarded as a strong favorable indicator for survival in pN0 patients independent of the pT stages (p<0.001 for all the pT stages).

Fig. 3

OS by quartiles of probability of false-negative LN in nodal-negative patients with T1 stage (A), T2 stage (B), and T3 stage (C) by Kaplan-Meier curves.

LN, lymph node; OS, overall survival; NSS, nodal staging score.

DISCUSSION

Our study demonstrates that it is not accurate to regard all pN0 as nodal-negative; the model of NSS could be used to assess the rationality of nodal-negative staging, revealing the real status of LN metastasis in EOC patients.

From a clinical perspective, computed tomography remains a widely-used imaging modality in the preoperative evaluation of tumors; however, it has a low sensitivity in describing tumor dissemination of EOC [11]. In addition, intraoperative palpation, as a traditional method for surgeons to detect LN metastasis, is not accurate enough to evaluate the real status of LN, when the tumor presents with deposits <2 mm in diameter [12]. LN is sometimes microscopic and again enlarged due to benign inflammatory processes, which makes visual judgment compromised. Thus, we believe that neither preoperative prediction, nor intraoperative estimation, is accurate enough to reveal the real status of LNs.

In a meta-analysis of retrospective studies, the incidence of occult LN disease in an apparent early-stage and low-grade EOC is 2.9% [13], indicating that a routine LN biopsy is inadequate for the nodal staging of EOC, and thus may have a high probability of leading to occult nodal disease undetected. In consistence with the previous findings, we found that the prevalence of a nodal disease was 5.28% in patients with pT1 stage EOC, but soared to 8.06% after adjusting for the probability of missing a nodal disease, indicating that 2.78% of patients suffered from an occult nodal disease. As we know, the pattern of postoperative therapy was distinct between advanced stage patients and those with an early stage EOC. Therefore, NSS is helpful to make an objective assessment on the optimal postoperative strategy for pN0 patients by quantifying the probability of understaging (1-NSS).

NSS is established based on a β-binomial model [14], taking into account a binomial distribution of patients as well as a heterogeneous distribution of P (FN) among patients. According to the principle of randomization, the data was divided into 2 datasets. The first dataset was used to simulate the real condition of missing a LN, followed by constructing β-binomial model in combination with the remaining data. Unlike the previous reports with similar methods [5 6 7], our simulation provides a more accurate fitting to the real conditions. Also, the model is under the assumption that there are no false-positive LNs during pathological examination in the patients labeled with LN-positive. In clinical practice, pathologists may declare a LN positive disease precisely as much as possible due to efficient teamwork and mutual supervision. Thus, it is obvious that this assumption is reasonable. Given the superiority that the adequacy of a nodal-negative determination can be quantified and its high predictive ability on survival, NSS is expected to be used in intraoperative prediction and postoperative clinical decision-making.

To avoid an occult LN disease, we recommend that the minimal number of LNs be examined and stratified by the pT stage, as an ancillary method to make more correct staging. NSS provides an objective assessment, enabling us to calculate the probability of occult nodal disease quantitatively by 1-NSS in a more visual way. To minimize the probability of missing a nodal disease, our results support that for pT2 patients, at least 5 nodes should be examined to ensure a reasonable LN evaluation with an accuracy of 90%. Likewise, at least 29 nodes should to be examined with an accuracy of 90% for pT3 patients. It seems remarkable that examination of even a single node in pT1 patients could provide an NSS of more than 90%, suggesting a low possibility of understaging for pT1N0 patients. With regard to pT3 patients, given 29 nodes to be examined, NSS is barely to acquire 90%. In the case of pT certainty, 90% accuracy is a reasonable estimate that could be recommended to assist preoperative evaluation and pathologic diagnosis, more importantly, assist FIGO staging system to reflect the real status of tumor disseminating more correctly. Moreover, the number of LNs as estimated by NSS could also be applied to predict prognosis of patients after LNE.

Positive LN status is a poor prognostic factor in early ovarian cancer, however, its role in advanced ovarian cancer (AOC) remained elusive. Recently, a prospective randomized trial was performed to evaluate the role of systematic pelvic and para-aortic LNE in patients with AOC. And the researchers found that systematic pelvic and para-aortic LNE in AOC patients with both intra-abdominal complete resection and clinically negative LN neither improve overall nor progression-free survival. However, despite detecting sub-clinical retroperitoneal LN metastases in 56% of the patients, no comparison in terms of survival between the LN positive and LN negative patients was performed in the study [15]. In our study, we highlight the use of NSS model to estimate the optimal numbers of LNs to avoid occult nodal diseases, and also give us a hint that patients with negative LNs detected could also have impact on overall survival. Also, serious postoperative complications and greater early mortality following surgery such as lymphedema should also be concerned in clinical practice.

To the best of our knowledge, this is the first study estimating the accuracy of nodal-negative diagnosis on EOC. However, the study also has some limitations. First, our study was retrospective without detailed information regarding the treatment information. However, this limitation is not relevant to this analysis. Second, the model we used was based on assumptions that there are no false-positive LNs among patients with LNs examined and that all LNs are equally accessible, which should be considered as a limitation, because it may differ from the real situation in clinical practice. Strictly speaking, this assumption is biologically untenable, but the bias resulted from this assumption would be minimal if only the number of examined nodes is the strongest factor. Furthermore, some studies concerning nodal dissection demonstrated support to this argument. For example, almost 75% of women with nodal metastases had positive nodes in the aortic area with or without concomitant pelvic nodal metastases [16 17 18]. These studies suggest a lack of orderly progression in LN metastases which offers circumstantial support for this study. In addition, there are a number of possible confounders that affect indications for the decision to dissect LNs and the likelihood that a positive node is removed from a patient, such as tumor grade, other sites of disease, status of the tumor capsule, and so on. The data were from SEER database, and was under the assumption that those confounders were neglectful and were homogeneous.

In brief, NSS, as an auxiliary tool, could assist surgeons to explore the real status of LN and assist the FIGO staging system to reflect tumor disseminating more correctly, and also provide preoperative prediction on LN resection yields and postoperative evaluation for further clinical decision-making. Taken together, it is feasible that once validated by prospective data, NSS can be applied to clinical managing EOC patients routinely.

Notes

^{Conflict of Interest} No potential conflict of interest relevant to this article was reported.

^{Author Contributions}

Conceptualization: L.L., C.L., X.Y.
Data curation: T.X., L.L.
Formal analysis: L.H., L.L., T.X.
Investigation: L.H., L.L., T.X.
Methodology: L.H., P.Y., C.L., X.Y.
Project administration: L.H., C.L., X.Y.
Software: L.H., L.L.
Supervision: X.Y.
Validation: P.Y.
Writing - original draft: L.L.
Writing - review & editing: C.L., T.X., X.Y.

References

1. Torre LA, Bray F, Siegel RL, Ferlay J, Lortet-Tieulent J, Jemal A. Global cancer statistics, 2012. CA Cancer J Clin. 2015; 65:87–108.

2. Trimbos JB, Vergote I, Bolis G, Vermorken JB, Mangioni C, Madronal C, et al. Impact of adjuvant chemotherapy and surgical staging in early-stage ovarian carcinoma: European organisation for research and treatment of cancer-adjuvant chemotherapy in ovarian neoplasm trial. J Natl Cancer Inst. 2003; 95:113–125.

3. Chan JK, Munro EG, Cheung MK, Husain A, Teng NN, Berek JS, et al. Association of lymphadenectomy and survival in stage I ovarian cancer patients. Obstet Gynecol. 2007; 109:12–19.

4. Morgan RJ Jr, Armstrong DK, Alvarez RD, Bakkum-Gamez JN, Behbakht K, Chen LM, et al. Ovarian cancer, version 1.2016, NCCN clinical practice guidelines in oncology. J Natl Compr Canc Netw. 2016; 14:1134–1163.

5. Prat J. FIGO Committee on Gynecologic Oncology. FIGO's staging classification for cancer of the ovary, fallopian tube, and peritoneum: abridged republication. J Gynecol Oncol. 2015; 26:87–89.

6. Gönen M, Schrag D, Weiser MR. Nodal staging score: a tool to assess adequate staging of node-negative colon cancer. J Clin Oncol. 2009; 27:6166–6171.

7. Kluth LA, Abdollah F, Xylinas E, Rieken M, Fajkovic H, Sun M, et al. Pathologic nodal staging scores in patients treated with radical prostatectomy: a postoperative decision tool. Eur Urol. 2014; 66:439–446.

8. Shariat SF, Rink M, Ehdaie B, Xylinas E, Babjuk M, Merseburger AS, et al. Pathologic nodal staging score for bladder cancer: a decision tool for adjuvant therapy after radical cystectomy. Eur Urol. 2013; 63:371–378.

9. Mattes MD, Bhatia JK, Metzger D, Ashamalla H, Katsoulakis E. Breast cancer subtype as a predictor of lymph node metastasis according to the SEER registry. J Breast Cancer. 2015; 18:143–148.

10. Iqbal J, Ginsburg O, Rochon PA, Sun P, Narod SA. Differences in breast cancer stage at diagnosis and cancer-specific survival by race and ethnicity in the United States. JAMA. 2015; 313:165–173.

11. Nasser S, Lazaridis A, Evangelou M, Jones B, Nixon K, Kyrgiou M, et al. Correlation of pre-operative CT findings with surgical & histological tumor dissemination patterns at cytoreduction for primary advanced and relapsed epithelial ovarian cancer: a retrospective evaluation. Gynecol Oncol. 2016; 143:264–269.

12. Girardi F, Petru E, Heydarfadai M, Haas J, Winter R. Pelvic lymphadenectomy in the surgical treatment of endometrial cancer. Gynecol Oncol. 1993; 49:177–180.

13. Lago V, Minig L, Fotopoulou C. Incidence of lymph node metastases in apparent early-stage low-grade epithelial ovarian cancer: a comprehensive review. Int J Gynecol Cancer. 2016; 26:1407–1414.

14. Magnussen S, Kremer A. The beta-binomial model for estimating heritabilities of binary traits. Theor Appl Genet. 1995; 91:544–552.

15. Harter P, Sehouli J, Lorusso D, Reuss A, Vergote I, Marth C, et al. LION: lymphadenectomy in ovarian neoplasms—a prospective randomized AGO study group led gynecologic cancer intergroup trial. J Clin Oncol. 2017; 35:15 suppl. 5500.

16. Signorelli M, Fruscio R, Ceppi L, Dell'anna T, Vitobello D, Chiappa V, et al. The role of pelvic and aortic lymphadenectomy at second look surgery in apparent early stage ovarian cancer after inadequate surgical staging followed by adjuvant chemotherapy. Gynecol Oncol. 2014; 132:312–315.

17. Negishi H, Takeda M, Fujimoto T, Todo Y, Ebina Y, Watari H, et al. Lymphatic mapping and sentinel node identification as related to the primary sites of lymph node metastasis in early stage ovarian cancer. Gynecol Oncol. 2004; 94:161–166.

18. Powless CA, Aletti GD, Bakkum-Gamez JN, Cliby WA. Risk factors for lymph node metastasis in apparent early-stage epithelial ovarian cancer: implications for surgical staging. Gynecol Oncol. 2011; 122:536–540.

TOOLS

ORCID iDs

Yuan Xu
https://orcid.org/0000-0002-3694-2871

Haoran Li
https://orcid.org/0000-0002-7046-9379

Xiaoxia Tong
https://orcid.org/0000-0001-8989-8643

Yangyang Pang
https://orcid.org/0000-0002-8687-2023

Xiaojuan Tong
https://orcid.org/0000-0003-4896-0855

Luhong Li
https://orcid.org/0000-0002-6728-0938

Lei Cheng
https://orcid.org/0000-0002-1568-5079

Similar articles