PDF
ePub
Citation
Print
I. Introduction
Spreading across all regions of the world, seasonal influenza is an acute respiratory infection caused by influenza viruses. The disease is estimated to affect more than one billion people, leading to 3 to 5 million severe cases, and 300,000 to 500,000 deaths annually [1]. Despite high annual rates of influenza and its threat to public health, understanding its behavior and key factors in virus transmission is challenging for public health experts and epidemiologists. Quantitative models and computer simulations are important tools to build and evaluate infectious disease theories. The standard approach to modeling the transmission dynamics of influenza viruses is to use conventional models, such as the susceptible-infected-recovered (SIR) and susceptibleexposed-infected-recovered (SEIR) models. However, the assumptions on which these models are based (e.g., the homogeneity of the underlying population) are not realistic in practice; therefore, several improved versions of the classic models have been developed in recent decades.
In total, a few quantitative studies have been conducted to investigate the association between environmental variables and influenza outbreaks in Iran. That is, the role of environmental factors in the severity and spread pattern of virus epidemics has remained under question [2345]. Early experimental studies showed that sun exposure reduces the survival of influenza viruses [6]. In another work, the authors pointed out that low temperatures and specific humidity increase influenza infection rates and its survival time [7]. Other results also have shown a correlation between absolute humidity and mortality rate [8]. On the contrary, recent experiments have shown that the epidemic peak time in temperate regions happens when the specific humidity content is at the highest level [910].
The potential burden of an influenza epidemic can be assessed by evaluating its transmission characteristics; one of the key parameters of influenza epidemic severity is the ‘effective reproductive number’, denoted by R, defined as the average number of secondary cases infected by one primary infected person [11]. Thus, when value of R is greater than one, the size of the infected population may increase or remain constant. Otherwise, the size of the infected population decreases [12].
The heterogeneity and diversity of the studies carried out on influenza modeling in Iran suggest that there is a need to focus more attention on influential factors, such as gender, population size, environmental factors, and latent conditions [13]. Hence, more comprehensive studies of the influence of external factors, such as environmental factors, on influenza contagion mechanisms and transmission dynamics in the area of interest are required. The central aim of this study was to develop a methodology based on the standard SIR model to enhance its performance by introducing environmental factors into the model. The proposed methodology investigates the behavior of the influenza virus subtype H3N2 because few studies have been conducted on this subtype in Iran [13] and it was the dominant virus from 2013 to 2015.
II. Methods
We used the weekly numbers of overall laboratory-confirmed influenza cases in Iran provided by World Health Organization (WHO) for two seasons, namely, 2013/14 and 2014/15 [14]. Climate data (precipitation, temperature, and specific humidity) from that period was obtained from the National Centers for Environmental Prediction-Department of Energy (NCEP-DOE) Reanalysis 2 data collection. The data is publicly available at the Earth System Research Laboratory (ESRL), which is a division of the National Oceanic and Atmospheric Administration (NOAA) [1516]. In the data preparation phase, the stream flow of the original climate data was downscaled from daily to weekly scale to make it consistent with the influenza data.
The SIR model is the backbone of mathematical modeling of epidemic diseases [17]. However, due to the sophisticated behavior of the influenza virus dynamics, many modified versions of the classic models have been developed [18]. Given that social and environmental parameters are among the important factors affecting influenza virus behavior, potential modifications can be made based on these factors [19]. In our investigation, the SIR model was used as the benchmark model. In the SIR model, the population is divided into three subgroups: susceptible (S), infected (I), and recovered individuals (R) [17]:
where β and γ are the transmission and recovery rates, respectively. In the following, an extended model is introduced, which incorporates the climate complementary data into the transmission rate from Equation (1):
where cis are constant coefficients that varied from −1 to 1; and P, T, and H are normalized precipitation, temperature, and specific humidity, respectively. Every one, two, or three possible combinations of these climate parameters correspond to a modified compartmental model. Simultaneously, each extended model is denoted by a notation consisting of ‘SIR’, ‘+’, and a set of letters from {P, T, H}. For example, the SIR+T+P model is constructed by combining the SIR model with temperature and precipitation.
The classical SIR model has shown great efficiency in capturing the non-linear nature of influenza dynamics; however, considering external factors, such as climate conditions that are not included in standard model, may yield more accurate and robust models. To validate the efficiency of the proposed approach, model parameters were estimated with Iran influenza data sourced from WHO. A straightforward iterative model-fitting strategy was used to estimate the unknown parameters for both the basic and extended models. In fact, the model parameters are initial conditions β and γ (and cis in the case of extended model). At each iteration step, all parameters are determined by minimizing the difference between observations and model predictions. At step n = k, the number of weekly influenza cases (model output) is calculated as
where β, S, and I are given from step n = k − 1, and the integration is done over week k. In the model-fitting methodology, the least-square cost function fits the model parameters θ = (S0, I0, β, γ) and, 
= (S0, I0, β, γ, c1…), which correspond to the null and extended models, respectively. In summary, if Zti and Yti are the estimated and real numbers of infected cases, minimizing the least-square function l(θ) = ∥Zt − Yt∥ will estimate the optimal values of θ and 
. It should be mentioned that the number of estimated parameters is varied from 5 to 7 unknown variables depending on the used climate factors.
= (S0, I0, β, γ, c1…), which correspond to the null and extended models, respectively. In summary, if Zti and Yti are the estimated and real numbers of infected cases, minimizing the least-square function l(θ) = ∥Zt − Yt∥ will estimate the optimal values of θ and . It should be mentioned that the number of estimated parameters is varied from 5 to 7 unknown variables depending on the used climate factors.The central part of the curve-fitting methodology is to minimize the objective cost function l(θ). The numerical solution of the optimization problem is obtained by using a constrained ‘Trust-Region’ algorithm. Meanwhile, at each iteration the numerical solution of the involved differential equations is calculated. All simulations were conducted in MATLAB. The model comparisons were performed by using the Akaike information criterion (AIC) and root-meansquare error (RMSE) criteria. Finally, for each case, the effective reproductive number, R(t) = S(t)β/γ, was calculated based on the estimated optimal parameters.
III. Results
To estimate the parameters of the classical and modified SIR models, a model-fitting methodology was used for the two influenza seasons of 2013/14 and 2014/15 in Iran. Two subsets were extracted from the WHO dataset consisting of the following: (i) 21 weeks of season 2013/14 starting from week 50 (2013) through week 18 (2014), and (ii) 26 weeks from week 46 (2014) to week 18 (2015). From a mathematical point of view, the SIR model has 4 unknown parameters (two initial conditions, β, and γ), and the proposed model, depending on its structure, consists of 5 to 7 parameters. Since specific humidity data did not significantly improve the model precision, it was not considered in the final implementation. Among all possible modifications of the original SIR model, the SIR+T, SIR+P, and SIR+P+T models are the most accurate in term of AIC and RMSE criteria.
The performance of the proposed models was measured by using the criteria of RMSE and AIC. To avoid the effects of noise in the peak interval, peak timing/magnitude were not used to evaluate the accuracy. Figure 1 shows the estimated weekly number of infections obtained from the three modified models and the original model (SIR, SIR+T, SIR+P, SIR+P+T).
As seen in Figure 1, the best fitted curve (red color) corresponds to the SIR+P+T model, which is a modification of the SIR model in which the transmission rate is adjusted by using temperature and precipitation. Two bar graphs in Figure 2 present the RMSE and AIC errors for three modified models and the SIR model. The SIR+P+T-based estimation errors, represented by solid black bars, have the lowest values. For this model, the RMSE decreased from 8.76 to 7.05 and from 8.57 to 6.45 compared to the benchmark model for seasons 2013/14 and 2014/15, respectively. Also, AIC decreased from 98.12 to 93.01 and from 118.69 to 107.91 for seasons 2013/14 and 2014/15, respectively. In summary, the embedded SIR model incorporating temperature and precipitation produces more precise results.
A residual error is the difference between observed values and the predictions made by a given model. The residuals show how far the data fall from the fitting curve and can be used to assess accuracy of a model. These errors versus predictions obtained from the standard and extended models (SIR+P+T) are presented in Figure 3. The asterisks and triangles respectively indicate SIR and SIR+P+T errors. As seen in the graph, the triangles are more accumulated around the x axis. Additionally, linear regressions of the errors are separately plotted for the two studied seasons (green and purple dashed lines correspond to the null and modified model, respectively). The lower slope of the green line compared to the purple line also indicates that SIR+P+T attained a higher precision than the SIR model.
Besides studying of possible extensions made by combination of the SIR model with three underlying climate factors, another important purpose of our study was the estimation of the effective reproductive number for both models. It should be mentioned that the basic reproductive number, R0 = β/γ, is a vital epidemic estimator. On the other hand, the effective reproductive number, which measures the average number of secondary cases for each primary infected individual at time t, can be estimated using R(t) = S(t)β/γ. As shown in Figure 4, the SIR+P+T-based estimation of R(t) for season 2013/14 lies between 0.36 and 2.10, while for the basic model, it varies from 0.21 to 3.34. Since the SIR+P+T model gives a more accurate prediction of the weekly number of cases, the estimated R(t) based on the extended model is more reliable.
IV. Discussion
This study highlighted the important role of environmental factors (e.g., temperature and precipitation) on influenza virus function by using modifications of the SIR model. The classical compartmental epidemic models, such as SIR and SEIR, divide the population into specific subgroups based on disease states and assign rates to every community member movement between these states. The time varying population of these subgroups and assigned rates are the key parameters of epidemic models. Despite the sophisticated nature of influenza, the simple SIR model successfully captures the essence of flu dynamics behavior; however, the underlying assumptions are not realistic. Two limitations of such approaches are the following. First, the assumption of the homogeneity of the underlying population causes failure to capture the real contact pattern of the population. Second, host sensitivity, disease transmission, and survival virus channels are not fully understood.
In this study, three modified models constructed by incorporating one or both of temperature and precipitation data into the SIR model were assessed in detail. A least-square fitting technique was used to estimate the model parameters from influenza and climate data. Then, the model performance was evaluated by using AIC and RMSE criteria. The key result of our investigation is that the embedding of auxiliary climate data into the SIR model led to accuracy improvement for the two studied seasons 2013/14 and 2014/15. In comparison to SIR-based estimates, the model incorporating precipitation and temperature achieved the best performance among the modified models. In the early stage of our study, we found that implementation of specific humidity data does not improve the model accuracy. As a clear limitation of our investigation, it should be noted that the average values of climate data and the total number of influenza cases were used; since Iran is a vast country with various types of climate, further investigations should be conducted to assess the performance of the proposed models in various provinces and cities.
Estimation of the basic and effective reproductive numbers for seasonal influenza can help authorities with resource allocation and making appropriate decisions. Calculation of the reproductive number is an indirect process because there is no analytical solution of model parameters that R(t) depends on. In other words, the effective reproductive number is an indirect product of the parameter estimation methodology. According to the formulae presented in the results section, we know that R(t) ≤ R0. In other words, R0 is the upper bound of the basic reproductive number. Equality occurs only when the entire population is susceptible. Since the whole population is not susceptible, it is more practical to use R(t) instead of R0. Based on our findings, time-varying R(t) function, derived from SIR+P+T based estimates, spans a narrower range of 0.36 to 2.10 in comparison to SIR-based estimations.
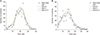
XML Download